9.     Fraktali – Mandelbrotov i Julijev fraktalni skup

9.1     Kompleksna ravnina i ravnina prikaza

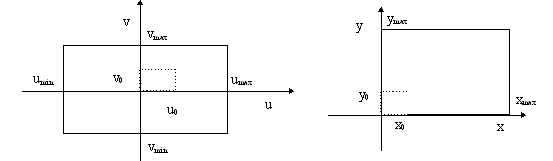
            Funkcija kompleksne varijable f(zn) promatra se u kompleksnoj ravnini čije su osi (u, v). Ravnina prikaza (x, y) je ravnina u kojoj prikazujemo promatranu kompleksnu funkciju. Prevođenje iz sustava (O u v) u sustav  (O' x y) ovisi o promatranom području u pojedinim sustavima. Neka je promatrano područje kompleksne funkcije zadano s umax, u min, v max i vmin. Područje sustava prikaza neka je zadano s rezx i rezy (Slika 10.1).

 

Slika 10.1. Ravnina kompleksne funkcije i ravnina prikaza.

           

            Sustav prikaza je zaslon, pa su vrijednosti na x i y osi diskretne. Koordinate točke u0 i v0 u kompleksnoj ravnini koje odgovaraju vrijednostima x0 i y0 su:

                                                        (1)

            Navedenim izrazima definirano je prevođenje iz jednog u drugi sustav.

9.2     Skupovi Mandelbrota i Julije

            Neka je zadano iterativno preslikavanje:

            ,                                                                                                    (2)

gdje je f(zn) na primjer , a c je odabrana točka kompleksne ravnine za koju ispitujemo konvergenciju generiranog niza. Za ovako definirano iterativno preslikavanje možemo promatrati da li niz koji generiramo (z0, z1, z2, ..) konvergira ili ne. Uvjet zaustavljanja u programskoj implementaciji može biti različit. Jedan primjer kriterija kojim ustanovljavamo da li niz konvergira je ocjena apsolutne vrijednosti:

           

            Ako iterativno preslikavanje zn+1 = f(z n) nakon n iteracija ne zadovolji uvjet  reći ćemo da niz konvergira, a inače da divergira. Definirat ćemo “brzinu divergencije” brojem iteracija koje su potrebne da uvjet  bude zadovoljen. Postupak se provodi tako da se za svaki slikovni element ravnine prikaza (x0, y 0) odredi pripadna točka kompleksne ravnine, te za nju ispita konvergencija pripadnog niza. Područje kompleksne ravnine unutar kojega iterativno preslikavanje generira konvergentne nizove naziva se Mandelbrot-ov skup.

            Za Julijev skup potrebno je odabrati  (točku kompleksne ravnine), a z0 je točka kompleksne ravnine za koju ispitujemo konvergenciju niza. Ako se za  odabere točka unutar Mandelbrot-ovog skupa Julijev skup će biti povezan, a inače nepovezan.

9.3     Radni zadatak

9.3.1     Postupak za Mandelbrotov skup:

            1. Učitati prag epsilon eps i maksimalan broj iteracija m.

            2. Učitati područje kompleksne ravnine koja se promatra (umin, umax), (v min, vmax).

            3. Pročitati razlučivost zaslona x max, ymax.

4.   Za svaku točku zaslona x0, y0:

     a) odrediti u0, v0  (prema formuli 1).

a)   Postaviti: k = -1, creal = u 0, cimag = v 0 , z0 = 0.

b)  Činiti:

                                    k = k + 1 ,

                                   

                                   

                        dok je ispunjen uvjet  r < eps i k < m :

              5. Na mjestu x0, y0 iscrtati slikovni element u boji k .

Primjer: eps=100, m=16, (umin, umax) = (-1.5, 0.5), (v min, vmax)=(-1, 1)

9.3.2     Postupak za Julijev skup:

            Postupak je sličan prethodnom, a promjene su:

            1. Dodatno učitati i kompleksnu konstantu .

a)   Postaviti: k = -1, zreal = u 0, zimag = v 0.

Primjer: eps=100, m=16, (umin umax)=(-1 1), (v min vmax)=(-1.2 1.2), (creal cimag)=(0.32 0.043).

 

            Slika 1: Mandelbrotov i Julijev fraktalni skup.