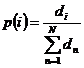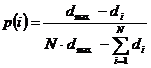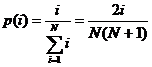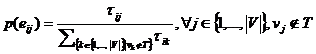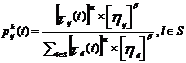Evolucijsko računanje je polje umjetne inteligencije koje se
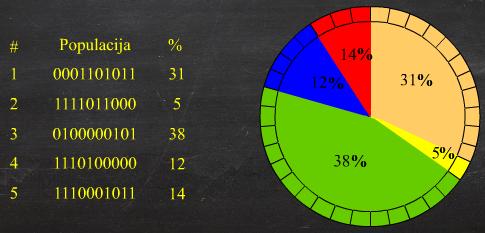
bavi rješavanjem optimizacijskih problema i problema pretraživanja. Algoritmi
evolucijskog računanja iskorištavaju iterativni proces razvoja populacije
jedinki i zasnovani su na biološkim mehanizmima evolucije.
Evolucijsko računarstvo je krovni pojam koji obuhvaća
nekoliko računarskih tehnika: genetsko programiranje (Koza, 1992.), evolucijske
strategije (Rechenberg, 1965.), evolucijsko
programiranje (Fogel, 1962.) i genetske algoritme (Holland, 1970.).
U ovom su radu opisana tri algoritma zasnovana na
evolucijskom računanju. U drugom je poglavlju opisan genetski algoritam. Pored
prirodnog modela evolucije, predočeni su pseudokod i
parametri algoritma, a načinjen je i pregled selekcije te genetskih operatora -
križanja i mutacije.
U trećem je poglavlju opisan algoritam optimizacije
kolonijom mrava. Povučena je paralela između ponašanja umjetnih mrava i mrava u
prirodi, a opisano je i modeliranje algoritma (konstrukcija rješenja i feromonski tragovi te parametri rješenja). Primjer
optimizacije prikazan je na problemu trgovačkog putnika.
Tema četvrtoga poglavlja je algoritam optimizacije rojem
čestica. Uz opis modela optimizacije, opisani su pseudokod
te parametri algoritma - evaluacija dobrote jedinke i ažuriranje brzine,
pozicije i najboljih rješenja jedinke.
Peto se poglavlje bavi praktičnom implementacijom -
vizualizacijom rada algoritama pomoću Flash
animacije. U ovom poglavlju opisane su svrha i organizacija animacije,
scenariji obrađenih algoritama i prikazani su obrađeni praktični primjeri
svakog algoritma.
Genetski algoritam (engl. Genetic Algorithm, GA)
je heuristički algoritam temeljen na evolucijskim principima selekcije i
genetike. Autor GA, John H. Holland,
predstavio je algoritam 1970-ih motiviran Darwinovom teorijom evolucije.
Osnovne tehnike GA zamišljene su tako da oponašaju procese u
prirodnim sustavima kojima se ostvaruje Darwinovo evolucijsko pravilo o
preživljavanju najboljih. Takve se tehnike mogu opisati na sljedeći način. Iz
populacije se selektira određeni broj jedinki. Selektirane jedinke smatraju se
dovoljno kvalitetnima za reproduciranje. Dobre se jedinke križaju kako bi
njihova djeca preuzela dobra svojstva svojih roditelja i time poboljšala
kvalitetu populacije u nadolazećim generacijama. Nakon križanja, pod
djelovanjem evolucijskog pritiska neke jedinke mutiraju. Izvođenje spomenutih
metoda nad populacijom jedinki rezultirat će dominacijom boljih jedinki nad
lošijima [8].
GA iskorištava evolucijske metode za pretraživanje prostora
rješenja kako bi pronašao rješenje optimizacijskog problema. GA je jedan od
algoritama zasnovanih na evolucijskom računanju.
Evolucija je konstantan proces prilagodbe jedinki
promjenjivim uvjetima staništa. Svaka jedinka ima određene osobine koje je
dobila evolucijskim procesom. Osobine jedinke definiraju jedinku, odnosno njenu
sposobnost brzini prilagodbe na nove uvjete u staništu. Jedinke s osobinama
koje u tom trenutku donose brže prilagođavanje na promjene u staništu imaju
veću sposobnost preživljavanja na razini vrste. Osobina koja pruža brze
prilagodbe na promjene staništa smatra se dobrotom jedinke. Jedinke sa
osobinama koje im omogućuju preživljavanje imat će veću vjerojatnost
reprodukcije čime će prenijeti svoje gene na potomke i doprinijeti razvoju
buduće generacije. Jedinke koje nose svojstva sa određenim nedostacima neće
nastaviti reprodukciju čime će takva svojstva sa vremenom evolucijski nestati.
Osobine jedinke zapisane su u kromosomima. Naime, svaki se
organizam sastoji od stanica, a u svakoj se stanici nalaze kromosomi. Kromosomi
su građeni od dvije lančaste molekule DNK. Kromosomi se sastoje od gena -
blokova DNK. Svaki gen šifrira protein koji predstavlja određenu osobinu
organizma. Dakle, geni su nositelji nasljednih osobina. Geni mogu biti
ravnopravni (oba dominantna ili oba recesivna) ili neravnopravni (jedan
dominantan, a drugi recesivan, pri čemu dominantan gen određuje nasljedno
svojstvo). Mogući oblik nasljedne osobine naziva se alel,
nalazi se na kromosomu i ovisi o kombinaciji dominantno-recesivnih gena.
Primjerice, ukoliko je osobina koju gen nosi boja očiju, alel
gena je plava boja očiju (ili zelena ili smeđa). Svaki gen ima svoju poziciju u
kromosomu koja se naziva lokus gena. Skup svih
kromosoma (cjelokupnog genetskog materijala) naziva se genom. Podskup gena u
genomu naziva se genotip. Fizičko ispoljavanje
genotipa naziva se fenotip. Fenotip je skup svih fizičkih i mentalnih osobina
organizma, odnosno fenotip je skup osobina jedinke koji se na njoj ispoljava.
Pod pretpostavkom da jedinka ima diploidan broj kromosoma
(2n), kada dvije jedinke izmjenjuju genetski materijal, njihov potomak dobiva
pola genetskog materijala od jednog roditelja (n), a drugu polovicu genetskog
materijala od drugog roditelja (n). Taj proces naziva se križanje. Genetski
materijal potomka može mutirati pod pritiskom evolucije. Mutacijom se smatra
greška u kopiranju genetskog materijala s nekog od roditelja na potomka i njome
se mijenja dio DNK odnosno geni, a time i osobine određene jedinke.
Kako GA oponaša evolucijske procese, metafore evolucije
prenose se i u računarsku terminologiju. U
Tablica
2.1 naveden je popis metafora i njihove računarske
istoznačnice.
Tablica
2.1 Usporedba evolucijske i
računarske terminologije
|
EVOLUCIJA
|
RAČUNARSTVO
|
|
Kromosom (=
skup gena)
|
Rješenje
problema
|
|
Gen (= dio kromosoma)
|
Dio rješenja
problema
|
|
Jedinka
(=kromosom)
|
Rješenje
problema
|
|
Populacija (=
skup svih kromosoma)
|
Skup svih
rješenja problema
|
|
Dobrota
jedinke
|
Dobrota
rješenja
|
Osnovni princip rada genetskog algoritma opisan je pseudokodom na Slika 2.1.
|
Generiraj početnu populaciju potencijalnih
rješenja P(t)
Evaluiraj svako rješenje
Dok nije zadovoljen uvjet završetka evolucijskog
procesa
Selektiraj
jedinke
Križaj
selektirane jedinke
Mutiraj
potomstvo
Evaluiraj
potomstvo
Loše
jedinke zamijeni dobivenim potomstvom
Ispiši najbolje rješenje
|
Slika 2.1 Pseudokod genetskog algoritma
Algoritam započinje fazom stvaranja početne populacije
jedinki odnosno inicijaliziranjem skupa kromosoma.
Početna je populacija najčešće nasumično generirana u granicama prostora
pretraživanja, kako bi se postiglo pretraživanje cijelog prostora rješenja.
Veličina populacije ovisi o tipu problema, no najčešće je veličine od nekoliko
stotina do nekoliko tisuća jedinki.
Postupkom selekcije iz početne se populacije odabire određeni
broj jedinki koje ulaze u reproduktivni proces (križanje i mutacija). Po
završetku mutacije, nove se jedinke evaluiraju i kopiraju u populaciju, a loše
se jedinke eliminiraju iz populacije. Proces selekcije i reprodukcije ponavlja
se u ciklusu dok nije zadovoljen uvjet završetka
(Slika
2.2) [4].
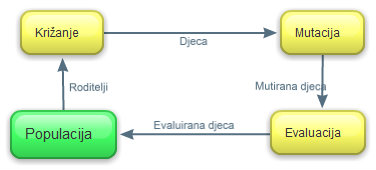
Slika 2.2 Reprodukcijski ciklus genetskog algoritma
Prostor pretraživanja (engl. search space) je
prostor svih mogućih rješenja problema. Jedno moguće rješenje u prostoru
pretraživanja predstavljeno je jednom jedinkom. Drugim riječima, prostor
pretraživanja je skup svih jedinki. Potencijalno rješenje problema dio je
prostora pretraživanja.
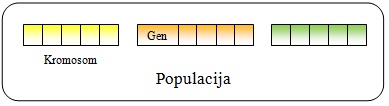
Slika 2.3 Struktura populacije
U genetskom algoritmu jedinku nazivamo kromosomom. Kromosomi
se sastoje od gena. Više kromosoma čine populaciju (Slika
2.3).
Svako rješenje (kromosom) može se evaluirati temeljem
vrijednosti njegove funkcije cilja. GA traži najbolje rješenje u skupu svih
dohvatljivih rješenja. U genetskom algoritmu, potraga za najboljim rješenjima
rezultira stvaranjem novih rješenja u skupu pretraživanja.
S obzirom na to da se svi podaci o jedinci čuvaju u
kromosomu (njen "izgled" i dobrota), prije početka implementiranja GA
algoritma za rješavanje bilo kojeg problema, potrebno je odabrati
najprikladniji način prikaza rješenja. Kromosomi se mogu prikazati na sljedeće
načine: binarnim prikazom, prikazom u obliku realnog broja, permutacijski i stablasto.
Binarni je prikaz
najučestaliji oblik prikaza rješenja pri uporabi genetskih algoritama. U binarnom
je prikazu svaki kromosom string ili polje koje se
sastoji od znamenki 0 i 1 (Slika
2.4).
|
Kromosom 1:
00010101010101010101
|
|
Kromosom
2: 10101010101001101010
|
Slika 2.4 Primjer binarnog prikaza kromosoma
Binarni prikaz koristan je jer se, čak i iz malog broja gena
(binarnih znamenki) može dobiti velik broj različitih kromosoma.
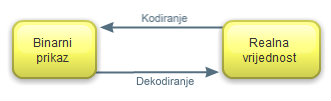
Slika 2.5 Shema kodiranja i dekodiranja binarnog
prikaza kromosoma
Kromosom kao binarni
vektor kodirana je realna vrijednost x
koja se nalazi u granicama intervala [dg,
gg] [8]. Iz binarnog vektora je moguće
saznati koja je njegova realna vrijednost provođenjem postupka dekodiranja.Dekodiranje je postupak kojim se binarni broj pretvara u
potencijalno rješenje problema, odnosno u realni broj x. Binarnom je kromosomu najprije potrebno izračunati njegovu
dekadsku vrijednost b, koja se računa
prema izrazu:
|
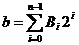
|
(2.1)
|
Vrijednost b važna je u postupku dekodiranja. Realna
vrijednost x izračunava se prema izrazu:
|
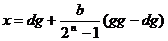
|
(2.2)
|
Suprotnim postupkom,
kodiranjem, određujemo dekadski broj b za zadani realan broj x:
|
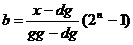
|
(2.3)
|
Dekadski se broj potom
pretvara u binarni prikaz. Važan parametar binarnog prikaza je i duljina
kromosoma te preciznost rješenja. Preciznost rješenja određuje duljinu
kromosoma [7]. Za zadanu preciznost p
kromosom ima duljinu n:
|
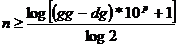
|
(2.4)
|
U jedan je kromosom moguće spremiti vrijednosti koje su u
intervalu [0, 2n-1]. U binarnom prikazu to su vrijednosti iz
intervala [00…00, 11..11].
Uz zadane vrijednost dg=0, gg=1, p=0.8, dobiva se duljina kromosoma od 3 bita. Prema tome, možemo
generirati ukupno 23, odnosno 8 jedinki. Njihova binarna, dekadska i
realna vrijednost prikazane su u
tablici 2.2.
Tablica 2.2 Primjer kodiranja i
dekodiranja vrijednosti binarnog kromosoma
|
Binarni prikaz
|
Dekadska
vrijednost b
|
Realna
vrijednost x
|
|
|
000
|
0
|
0
|
|
001
|
1
|
0.143
|
|
010
|
2
|
0.286
|
|
011
|
3
|
0.429
|
|
100
|
4
|
0.571
|
|
101
|
5
|
0.714
|
|
110
|
6
|
0.857
|
|
111
|
7
|
1
|
|
|
|
|
|
U slučaju višedimenzijskog problema implementiranog binarnim prikazom
kromosom čini polje brojeva veličine dimenzija problema [8].
Kromosom se može prikazati kao realan broj (broj s pomičnom
točkom jednostruke ili dvostruke preciznosti). Uporaba binarnog prikaza u
problemima koji zahtijevaju realni prikaz bila bi otežana. Kromosom se u ovom
načinu prikaza sačinjava od realnih vrijednosti (Slika
2.6).
|
Kromosom: 1.234 5.654 8.234 4.564
|
Slika 2.6 Prikaz kromosoma u obliku niza realnih
brojeva
Permutacijski se prikaz najčešće koristi pri rješavanju
problema čije je rješenje poredak (npr. problem
trgovačkog putnika ili problem rasporeda zadataka). U permutacijskom prikazu
svaki kromosom sadrži niz brojeva koji predstavljaju mjesto u ukupnom poretku (Slika
2.7).
|
Kromosom 1: 1 3 4 5 6 2
|
|
Kromosom 2: 6 1 3 2 4 5
|
Slika 2.7 Primjer permutacijskog prikaza kromosoma
2.4.4
Stablasti
prikaz
Stablasti se prikaz najčešće
koristi u evolutivnim programima (engl. evolving programs) ili
logičkim izrazima. Svaki je kromosom prikazan kao stablo objekata (Slika
2.8).
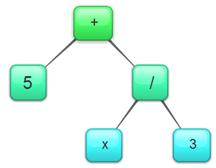
Slika 2.8 Primjer stablastog
prikaza kromosoma
Genetski algoritam ne zna prirodu dobivenog rješenja, tj. ne može odrediti njegovu kvalitetu. Iz toga razloga,
genetski algoritam ne može samostalno zaključiti je li dobiveno rješenje
ispravno te prekinuti daljnji evolucijski proces.
Uvjeti zaustavljanja određuju se prilikom modeliranja
problema. Kombinacija različitih uvjeta zaustavljanja može se također
iskoristiti kao kriterij zaustavljanja rada algoritma.
Uvjeti zaustavljanja rada genetskog algoritma mogu biti
sljedeći:
- Dosegnut je maksimalan
broj iteracija
- Dosegnut je maksimalan
broj evaluacije funkcije cilja
- Dostignuta je željena
vrijednost funkcije cilja
- Funkcija cilja nije se
promijenila već nekoliko iteracija
- Dostignuto je zadano
vremensko ograničenje izvođenja [7].
Selekcija je postupak odabira kromosoma iz trenutne
generacije P(t), koji će se izložiti
genetskim operatorima križanja i mutacije kako bi njihova djeca dala još bolja
rješenja problema.
Svrha selekcijskog procesa je očuvanje dobrih svojstava jedinki
i njihovo prenošenje na nove generacije jedinki [8]. Iz tog će razloga bolje jedinke imati veću vjerojatnost biti
izabrane za reprodukciju, a time i za preživljavanje.
Ovisno o načinu prenošenja boljih jedinki u sljedeću
generaciju, selekcijski se postupci dijele na generacijske i eliminacijske. U generacijskim selekcijama biraju se
jedinke iz trenutne generacije P(t) koje
se kopiraju u međupopulaciju P'(t). Jedinke iz međupopulacije potom
sudjeluju u reprodukciji (križanju i mutaciji). Nedostatak generacijskih
selekcija je što se dvije populacije jedinki istovremeno nalaze u memoriji.
Kako manje jedinki preživi selekciju nego što je u nju ušlo, nedostatak jedinki
nadomješta se kopiranjem jedinki iz početne populacije. Te jedinke ne doprinose
kvaliteti rješenja, već naprotiv, usporavaju algoritam.
Slika 2.9 Generacijska i eliminacijska
selekcija
|
|


U eliminacijskim se
selekcijama u svakoj iteraciji obriše M
jedinki, pri čemu je parametar M
mortalitet i predstavlja količinu jedinki koje će se izbrisati iz populacije.
Kako bi se populacija konstantnom eliminacijom jedinki smanjivala do
istrebljenja, eliminirane jedinke potrebno je nadomjestiti potomcima koji
nastaju reprodukcijom. Eliminacijskim se selekcijama uklanjaju problemi
generacijskih selekcija - u jednoj iteraciji postoji samo jedna populacija i
selekcijom se ne stvaraju duplikati [8].
Uvođenjem parametra M zanemarujemo
parametar vjerojatnosti križanja, jer se križanje mora provesti onaj broj puta
koliko je jedinki eliminirano (kako bi veličina populacije ostala
nepromijenjena).
Ovisno o tome kako se genetski materijal prenosi u sljedeću
generaciju, odnosno načinu određivanja vjerojatnosti odabira pojedine jedinke,
selekcije se dijele na proporcionalne i rangirajuće.
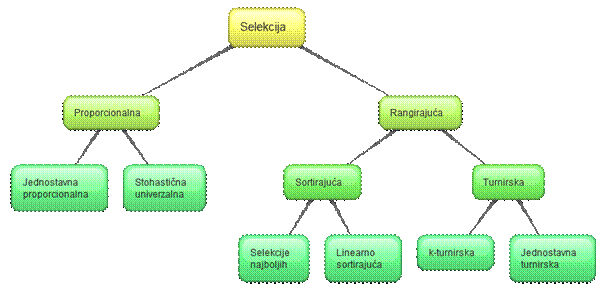
Slika 2.10 Podjela selekcije s obzirom na određivanje
vjerojatnosti odabira jedinke
Proporcionalne
selekcije čine podskup selekcija kod kojih je vjerojatnost odabira pojedine
jedinke ovisna o vlastitoj dobroti te srednjoj vrijednosti dobrote populacije i
jednaka je kvocijentu te dvije vrijednosti. Nedostaci proporcionalnih selekcija
su nužnost izračunavanja srednje vrijednosti dobrote populacije i translacije
funkcije dobrote u svakoj iteraciji. S obzirom na činjenicu da proporcionalne
selekcije ne čuvaju najbolje jedinke, u njih je potrebno ugraditi mehanizam
elitizma čime se, zbog sortiranja jedinki po dobroti, troši procesorsko vrijeme
i usporava se rad algoritma.
Rangirajuće selekcije čine podskup selekcija kod
kojih vjerojatnost odabira pojedine jedinke ovisi o poretku jedinki sortiranih
po dobroti. Pri rangirajućim selekcijama nije važan
iznos dobrote pojedine jedinke, već kakav je odnos tog iznosa prema
vrijednostima dobrote ostalih jedinki u populaciji. Ako dvije jedinke imaju
istu dobrotu, bilo koja od njih može se prenijeti u sljedeću generaciju.
Jednostavna proporcionalna selekcija (engl.
Roulette Wheel Selection)
selekcijski je proces kod kojeg je vjerojatnost odabira jedinke proporcionalna
dobroti jedinke.
Kod generacijske
proporcionalne selekcije, vjerojatnost selekcije jedinke i određuje se kao kvocijent dobrote
jedinke i ukupne dobrote svih jedinki iz populacije, prema izrazu (2.5).
|
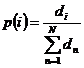
|
(2.5)
|
Jedan od načina izvođenja jednostavne proporcionalne
selekcije je da se u svakoj iteraciji za svaku jedinku izračuna vrijednost
njene kumulativne dobrote po izrazu (2.6). Kumulativna dobrota d(i) je suma vrijednosti dobrota jedinki
čija je oznaka manja ili jednaka od i [9].
|
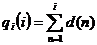
|
(2.6)
|
Vrijednosti
kumulativne dobrote postavljaju se na pravac duljine D, pri čemu je D ukupna dobrota
svih jedinki populacije (Slika
2.11) [7].
- Potom se generira
nasumičan broj r iz intervala
[0, 1]. Vrijednost broja r
određuje koja će se jedinka iz populacije P(t) kopirati u međupopulaciju. Iz P(t) selektira se jedinka s indeksom i, ako se nasumičan broj r nalazi u intervalu [q(i-1), q(i)].
Ukupan broj odabranih jedinki u međupopulaciji
mora biti jednak veličini početne populacije P(t). Jedna se jedinka može kopirati u P'(t) više puta.
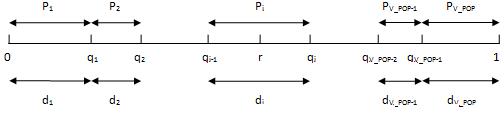
Slika 2.11 Jednostavna proporcionalna selekcija
Algoritam jednostavne proporcionalne generacijske selekcije
opisan je sljedećim pseudokodom:
Izračunaj
ukupnu dobrotu svih jedinki
Izračunaj vjerojatnost odabira svake jedinke po izrazu (2.5)
Izračunaj
kumulativnu dobrotu jedinke i, po izrazu
(2.6)
Ponavljaj
dok broj jedinki u međupolaciji nije jednak broju
jedinki početne populacije
Generiraj nasumični broj r između 0 i 1
Ako je q(i-1) < r <
q(i) jedinku i kopiraj u međupopulaciju
|
Slika 2.12 Pseudokod jednostavne proporcionalne selekcije
Zbog načina odabira jedinki česta je analogija jednostavne
proporcionalne selekcije s kotačem ruleta (Slika 2.13). Pri tom se kumulativna dobrota jedinki,
umjesto na pravac, slaže na obod kotača ruleta, a nedeterministički odabir
broja r simbolizira okretanje kotača
ruleta.
Slika 2.13 Kotač ruleta
Nedostaci ove selekcije su: dobrota jedinke uvijek mora biti
pozitivna, dobra jedinka imat će previše kopija u novoj populaciji, vrijednost
dobrote često se mora skalirati [7].
Ako je dobrote jedinke negativna izrazi (2.5) i (2.6) neće vrijediti. Problem
negativne vrijednosti funkcije dobrote rješava se postupkom translacije tako da
se od dobrote jedinke oduzme minimalna vrijednost funkcije dobrote svih jedinki
(2.7).
|
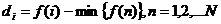
|
(2.7)
|
Osim translacijom, problem negativnih vrijednosti funkcije
cilja može se riješiti linearnom normalizacijom ili sortiranjem. Taj se
postupak svodi na sortiranje jedinki po dobroti.
U eliminacijskoj proporcionalnoj selekciji ne koriste se
dvije populacije i ne stvaraju se duplikati. Vjerojatnost eliminacije jedinke i računa se prema izrazu (2.8).
|
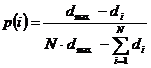
|
(2.8)
|
U eliminacijsku je selekciju ugrađen elitizam jer se
najbolja jedinka ne može eliminirati.
Stohastička univerzalna selekcija veoma je slična prethodno
opisanoj jednostavnoj proporcionalnoj selekciji od koje se razlikuje u načinu
odabira jedinki.
|
Izračunaj
ukupnu dobrotu svih jedinki
Izračunaj vjerojatnost odabira svake jedinke po izrazu (2.5)
Podijeli
jedinični interval na N+1 dijelova pri čemu početak svakog od N intervala predstavlja
jednu značku
Za
svaku značku
Jedinku na koju pokazuje značka kopiraj u međupopulaciju P'(t)
|
Slika 2.14 Pseudokod stohastičke univerzalne selekcije
Slika 2.15 Stohastička univerzalna selekcija
Stohastička univerzalna selekcija sve jedinke dohvaća u
jednom koraku za razliku od jednostavne selekcije koja jedinke dohvaća u N
koraka.
2.6.4
Rangirajuće
selekcije
Za razliku od proporcionalnih selekcija kod kojih je
vjerojatnost odabira jedinke ovisila o dobroti jedinke, kod rangirajućih
selekcija vjerojatnost odabira jedinke ne ovisi o njenoj dobroti već o položaju
jedinke u poretku po dobroti.
Sortiramo li jedinke po rastućoj vrijednosti dobrote (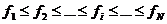 ), najbolja će jedinka imati indeks N, a najlošija 1.
Obrnuto, sortiramo li jedinke po padajućoj vrijednosti dobrote (
), najbolja će jedinka imati indeks N, a najlošija 1.
Obrnuto, sortiramo li jedinke po padajućoj vrijednosti dobrote (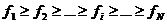 ), najbolje će biti jedinka s indeksom 1, a najlošija će
imati indeks N.
), najbolje će biti jedinka s indeksom 1, a najlošija će
imati indeks N.
Kako kod rangirajućih selekcija nema
ograničenja na funkciju cilja, funkcija cilja jednaka je funkciji dobrote.
Rangirajuće se selekcije dijele na
sortirajuće i turnirske. Sortirajuće
selekcije sortiraju jedinke u ovisnosti o funkciji cilja. Turnirske selekcije
promatraju odnos dobrote između nekoliko slučajno odabranih jedinki iz cijele
populacije pri čemu nije potrebno sortirati cijelu populaciju.
Linearno sortirajuća selekcija je
selekcija kod koje je vjerojatnost selekcije pojedine jedinke veća što je veći
njen rang tj. što je bolji položaj jedinke u poretku
po dobroti. Vjerojatnost selekcije jedinke računa se prema izrazu (2.6):
|
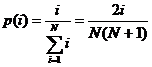
|
(2.6)
|
Razlikujemo generacijsku i eliminacijsku linearno sortirajuću selekciju. Navedena dva tipa selekcije
razlikujemo po položaju najbolje i najlošije jedinke u populaciji. Tako će u
generacijskoj selekciji najbolja jedinka biti ona s indeksom N, a najgora ona s
indeksom 1. Naprotiv, u eliminacijskom će algoritmu najbolja jedinka biti ona s
indeksom 1, a najgora će biti jedinka s indeksom N.
Obilježje k-turnirskih
selekcija je što se s jednakom vjerojatnošću odabire k jedinki iz populacije. Iz tog podskupa veličine k elemenata selektira se najbolja ili
najlošija jedinka, ovisno o problemu koji se rješava. Parametar k označava veličinu turnira odnosno broj
jedinki koje se selektiraju iz početne populacije.
Razlikujemo generacijsku i eliminacijsku k-turnirsku selekciju. U generacijskoj k-turnirskoj selekciji slučajno se
odabire podskup od k jedinki onoliko
puta kolika je veličina početne populacije (N).
Najbolja od njih u svakoj iteraciji kopira se u međupopulaciju
P'(t).
Slika 2.16 3-turnirska generacijska
selekcija
|
|


U eliminacijskoj k-turnirskoj selekciji slučajno se odabire
podskup od k jedinki onoliko puta kolika
je stopa mortaliteta M. Najgora od
odabranih jedinki se eliminira. Eliminirana se jedinka nadomješta djetetom
dviju slučajno odabranih jedinki.
Slika
2.17 3-turnirska eliminacijska
selekcija
|
|

Kako bi se ostvarila k-turnirska selekcija, ne moraju se
sortirati sve jedinke, već se samo promatraju vrijednosti funkcije cilja između
jedinki u podskupu k jedinki.
U k-turnirsku
selekciju inherentno je ugrađen elitizam jer se najbolja jedinka nikako ne može
eliminirati. Naime, uvijek će postojati k-1
jedinki koje su lošije od najbolje jedinke. Drugim riječima, vjerojatnost
eliminacije najbolje jedinke jednaka je nuli.
Jednostavna turnirska selekcija specifičan je oblik
eliminacijske binarne turnirske selekcije prilagođene za paralelno izvođenje.
U prvom koraku nasumičnim se odabirom iz populacije odabere
jedan par jedinki. Lošija od dviju jedinki se eliminira. Iz preostale
populacije (koja uključuje i ranije izabranu neeliminiranu jedinku) izabire se
novi par jedinki. Teoretski, drugoizabrana jedinka
može biti jedinka koja je već selektirana u prvoj selekciji. Lošija od njih
također se eliminira. Izabrani par jedinki podvrgava se operatorima križanja i
mutacije. Jedinke se potom evaluiraju, nakon čega se pohranjuju u početnu populaciju.
Nove su jedinke u populaciju donijele dobre osobine svojih roditelja i
nadomjestile su eliminirane jedinke čime je broj jedinki u populaciji
nenarušen.
|
Slučajnim
postupkom izaberi dvije jedinke
Roditelj_A
= bolja od dvije selektirane jedinke
Eliminiraj
lošiju jedinku
Slučajnim
postupkom izaberi dvije jedinke od preostalih jedinki
Roditelj_B
= bolja od dvije selektirane jedinke
Eliminiraj
lošiju jedinku
Djeca
= rezultat križanja roditelja
Mutiraj
djecu
Evaluiraj
djecu
Djecom nadomjesti eliminirane jedinke
|
Slika 2.18 Pseudokod jednostavne turnirske selekcije
Križanje je genetski operator kojim
se omogućuje prenošenje svojstva jedinke s roditelja na djecu. Križanje je
postupak izmjene gena između roditelja.
Jedinke se križaju kako bi se
zadržala dobra svojstva populacije. Što je dobrota jedinke veća, veća je i
njena vjerojatnost preživljavanja i križanja. Križanjem se može stvoriti jedno
ili dvoje djece. Svrha križanja je dobiti djecu koja će biti jednako dobra ili
bolja od svojih roditelja.
Postoji mogućnost da nakon križanja,
a potom i mutacije, nastalo dijete bude identično nekoj od jedinki u
populaciji.
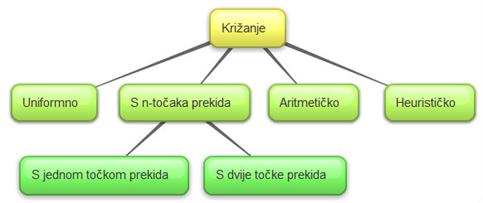
Slika 2.19 Podjela operatora križanja
Kod križanja s n-točaka prekida,
najprije se definira parametar n. N kazuje u koliko će se točaka prekida
razdvojiti genetski materijal jedinki.
Osim parametra n, potrebno je definirati iza kojih će se bitova dogoditi prekid
genetskog materijala. Te se pozicije nazivaju točke prekida. Najčešće se
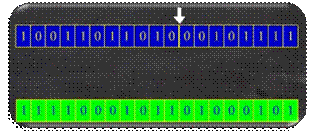
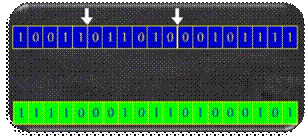
koristi križanje s jednom ili dvije točke prekida. Na Slika 2.20 prikazano je križanje s jednom točkom prekida
iza 20. bita.
Slika 2.20 Križanje s jednom točkom prekida
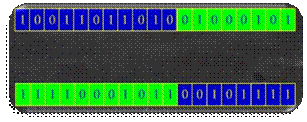
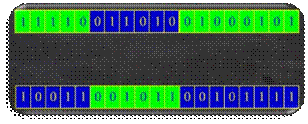
Na slici 2.21 prikazano je križanje s dvije točke
prekida iza 5. i 17. bita.
Slika 2.21 Križanje s dvije točke prekida
Križanjem može nastati jedno ili
dvoje djece. Prvo dijete nastaje tako da se početni dio genetskog materijala
uzima od prvog roditelja, sljedeći od drugog roditelja te tako naizmjeničnom rekombinacijom dok dijete ne postane jednake veličine kao i
njegovi roditelji. Drugo dijete generira se kao i prvo s razlikom da se prvi
dio genetskog materijala uzima od drugog roditelja.
Segmentno križanje je križanje s
velikim brojem točaka prekida, pri čemu je broj točaka i pozicija prekida
slučajan za svako križanje.
Pri uniformnom križanju vjerojatnost da će dijete
naslijediti gen od prvog ili drugog roditelja jednaka je (p=0.5). Uniformno se
križanje može ostvariti na nekoliko načina:
1. Generiranjem
vjerojatnosne maske - generira se maska čija je
veličina jednaka duljini kromosoma i koja na svakoj lokaciji ima zapisano s
kojom se vjerojatnošću preuzima gen od prvog roditelja. Kada vjerojatnosti
nasljeđivanja pojedinih gena nisu iste za sve gene govorimo o p-uniformnom križanju
(npr. ako je p=0.4, vjerojatnost da dijete preuzme
gen od prvog roditelja je 40%, a od drugog roditelja je 60%).
2. Aritmetičkom
operacijom - dijete se generira pomoću aritmetičke funkcije
DIJETE = A*B + R*(A
XOR B),
Pri čemu je R nasumično generirani vektor koji se sastoji od nula i jedinica.
Komponenta A*B osigurava nam da
zadržimo gene u kojima su roditelji isti, a ostatak postavimo na vrijednost
nula. Komponentom R*(A XOR B)
generiraju se slučajni bitovi na mjestu gdje su kromosomi različiti.
3. Promatra
se nasumično generirani vektor R. Pri
generiranju prvog djeteta, ukoliko je vrijednost bita u R na i-toj poziciji jednaka
0, vrijednost i-tog bita prvog
djeteta preuzet će se od prvog roditelja. Ukoliko je ta vrijednost u R jednaka 1, vrijednost biti djeteta
preuzima se od drugog roditelja.
Pri generiranju drugoga djeteta,
ukoliko je vrijednost bita u R na i-toj poziciji jednaka 0, vrijednost i-tog bita prvog djeteta preuzet će se
od drugog roditelja. Naprotiv, ukoliko je ta vrijednost u R jednaka 1, vrijednost bita djeteta preuzima se od prvog
roditelja.


Aritmetičko se križanje koristi kod prikaza rješenja u
obliku realnih brojeva. Djeca se stvaraju temeljem sljedećih izraza:
Dijete1 = a * roditelj1 + (1-a) * roditelj2
Dijete2 = (1-a) * roditelj1 + a * roditelj2
Pri čemu je a
težinski faktor koji se odabire prije križanja [13].
Kod heurističkog križanja koristi se vrijednost funkcije
dobrote dvaju roditelja kako bi se generiralo dijete. Heurističko se križanje
koristi pri prikazu rješenja u obliku realnih brojeva.
Djeca se generiraju prema sljedećim izrazima:
Dijete 1 = bolji roditelj + r * (bolji roditelj - lošiji roditelj)
Dijete 2 = bolji roditelj
Pri čemu je r
nasumičan broj između nule i jedan [13].
Moguće je da se prvo dijete ne može generirati. To se može
dogoditi ako se jedan ili više gena nalaze van granica inicijalno zadanog
početnog intervala pretraživanja. Iz tog se razloga u heurističkom križanju
koristi podesivi parametar n kao
mjera broja pokušaja koliko će se puta pokušati generirati nova vrijednost r, koja bi rezultirala genom čija je
vrijednost unutar granica intervala. Ukoliko se ni nakon n pokušaja ne uspije generirati ispravni gen, dijete poprima
vrijednost lošijeg roditelja.
Prije križanja jedinki, dobro je provjeriti jesu li
roditelji identični. Osim što bi se radio veći posao (dovoljno je samo kopirati
jednog roditelja), dobila bi se duplicirana jedinka čime kvaliteta rješenja ne
bi narasla, već bi duplikat dodatno usporavao algoritam.
Mutacija je genetski operator koji
utječe na promjenu gena u kromosomu. Mutacija djeluje nad jednim kromosomom
čiji se geni mijenjaju s vjerojatnošću kojeg određuje vjerojatnost mutacije pm. Vjerojatnost mutacije je
parametar genetskog algoritma. Kromosom nakon mutacije (teoretski) može biti u
cijelosti promijenjen, što omogućava mutaciji bolje pretraživanje prostora.
Svrha mutacije je bolje istražiti
prostor rješenja i time izbjeći lokalne optimume. Naime, većina algoritama
temeljenih na populaciji roja ima problem s preranom konvergencijom. Taj se
problem javlja kada se reprodukcijom dobrih jedinki stvori velik broj sličnih,
također dobrih jedinki, u preranoj fazi evolucije. Ako su najbolje jedinke koje
se križaju ujedno i lokalni optimumi, njihovo će potomstvo također biti u
blizini lokalnog optimuma. Mutacija sprečava
jedinke da postanu previše slične. Iz tog se razloga ne mutiraju samo najbolje
jedinke, već se odabir jedinki vrši u cijelosti ili djelomično nasumično.
Odabiru vjerojatnosti mutacije
potrebno je pristupiti oprezno. Ako je vjerojatnost mutacije prevelika,
algoritam će se presporo približavati globalnom optimumu, a pretraživanje prostora
odvijat će se nasumično. Ako je vjerojatnost mutacija preniska, malo će se
bitova u kromosomu promijeniti pa će istraživanje prostora biti presporo [13].
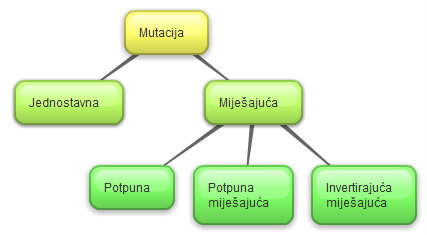
Slika 2.23 Podjela mutacije
Jednostavna mutacija oblik je
mutacije pri kojem se svaki bit kromosoma mijenja s jednakom vjerojatnošću.
Odluka hoće li se bit promijeniti ili ne, ovisi o parametru vjerojatnosti
mutacije (Slika 2.24).
|
Za
svaki bit kromosoma
Generiraj nasumični broj r iz intervala [0, 1]
Ako je r
manji od vjerojatnosti mutacije
Promijeni vrijednost bita
|
Slika 2.24 Pseudokod jednostavne mutacije
Teoretski, svi bitovi pojedinog
kromosoma mogu biti promijenjeni. U tom slučaju riječ je o potpunoj inverziji
kromosoma. U praksi je vjerojatnost da se opisana situacija dogodi mala jer je
vrijednost vjerojatnosti mutacije pojedinog bita veoma mala.
Tablica 2.3 Primjer jednostavne mutacije
|
Kromosom
00101110
|
Mutirani kromosom
|
r
|
r < p_m
|
|
00101110
|
|
0.45
|
NE, nema promjene
|
|
00101110
|
01101110
|
0.002
|
DA, mutiraj bit
|
|
01101110
|
|
0.86
|
NE, nema promjene
|
Zajednička osobina mutacija opisanih
u nastavku je odabir gornje i donje granice intervala na selektiranom kromosomu
za mutaciju tako da su zadovoljeni sljedeći uvjeti:
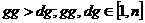
Mutacija se provodi nad odabranim intervalom [13].
U miješajućoj se mutaciji svi geni
iz odabranog intervala međusobno pomiješaju tako da im se indeks trenutne
pozicije u kromosomu zamijeni s nekim drugim indeksom u granicama [0, VELIČINA_KROMOSOMA]. Pri takvoj
mutaciji, broj nula i jedinica u kromosomu ostaju nepromijenjeni.
Kada nad intervalom kromosoma
djeluje potpuna miješajuća mutacija, svi se bitovi unutar zadanog intervala
slučajno generiraju čime se mijenja struktura kromosoma.
Invertirajuća miješajuća mutacija
invertira sve bitove u zadanom intervalu.
Potpuna mutacija poseban je oblik
miješajuće mutacije pri kojoj su gornja i donja granica intervala rubovi
kromosoma što uzrokuje miješanje svih gena u kromosomu. I u ovom slučaju broj
nula i jedinica ostaju nepromijenjeni.
Algoritam optimizacije kolonijom mrava (engl. Ant Colony Optimization, ACO)
jedan je od najpoznatijih algoritama za približnu optimizaciju (engl. approximate optimization).
Njegov autor, Marc Dorigo,
ranih je 90-ih predstavio novi algoritam za koji je motivaciju pronašao u
ponašanju mravlje kolonije prilikom potrage za hranom [2].
Mravi su društvene životinje. Žive u zajednicama
(kolonijama) i njihovo je preživljavanje vođeno instinktom za pronalaženjem
hrane. Pri tome, svoje interese podređuju interesima kolonije, čiju dobrobit
podređuju vlastitoj.
Otkriveno je kako mravi prilikom potrage za hranom imaju
sposobnost pronalaženja najkraćeg puta od kolonije do izvora hrane. Spomenuto
je ponašanje prikazano u eksperimentu znanstvenika Gossa.
Goss je proveo eksperiment s kolonijom argentinskih
mrava (Iridomyrmex humilis). U
eksperimentu, mravima iz kolonije dana su dva puta kojima mogu doći do izvora
hrane. Iako oni toga nisu svjesni, jedan put duži je od drugog [11].
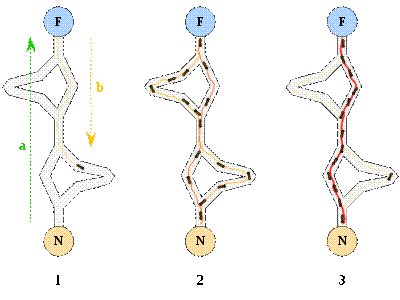
Slika 3.1 Gossov eksperiment pronalaska najkraćeg puta
Razlog zašto navedeni eksperiment ima veliku težinu nalazi
se u tome što argentinski mravi nemaju dobro razvijen vid stoga se na njega ne
mogu ni osloniti. Argentinski su mravi, prilikom potrage za hranom, vođeni drugim
osjetilom - mirisom.
Prilikom kretanja, mravi na prijeđenom putu ispuštaju feromone - mravlji kemijski (hormonski) trag. Feromoni imaju olfaltilna i volativna svojstva - može ih se namirisati i isparljivi su.
Feromoni imaju ulogu usmjeritelja. Naime,
istraživanje je pokazalo da će mrav koji kreće iz kolonije s većom
vjerojatnošću odabrati onaj put do hrane na kojem osjeti jači miris feromona.
Pri grananju puta na dvije dionice, vjerojatnost da će mrav
odabrati bilo koju od dionica, jednaka je. Kako kretanje po kraćoj dionici
zahtjeva manje utrošenog vremena za pronalazak hrane, u istom će je vremenu
prijeći veći broj mrava. Što više mrava odabere isti put, na njemu će ostaviti
veću količinu feromona.
Kako feromoni nakon nekog vremena
isparavaju, ako nekim putem prolazi manji broj mrava, feromoni
se na toj dionici puta neće osjetiti i s vremenom će ispariti. Zbog nedostatka feromona, nove mrave taj put neće ni privući, a s vremenom
će svi mravi prijeći na najkraći put.
Ovakav način komunikacije prirodnih mrava naziva se stigmerija - mravi međusobno komuniciraju indirektno putem
modifikacije okoline - jedna jedinka mijenja okolinu, a druga reagira na novu,
modificiranu okolinu. Time se ostvaruje horizontalni tok komunikacije jer sve
jedinke mogu komunicirati s ostalim jedinkama putem okoline [10].
Kako bi se objasnilo ponašanje umjetnih mrava, potrebno je pojednostaviti
njihov prirodni model ponašanja opisan u eksperimentu iz prethodnoga poglavlja.
Neka je okolina kojom se mravi kreću oblikovana kao graf G = (V, E),
pri čemu je V skup od dva vrha: vs (predstavlja koloniju) i vd
(predstavlja izvor hrane). E je skup
od dva brida, e1 i e2 koji spajaju vrhove vs i vd. Bridu e1 pridjeljujemo duljinu l1, a bridu e2 pridjeljujemo duljinu l2, pri čemu je l2 > l1.
Svaki mrav započinje gibanje u čvoru vs s ciljem kretanja k čvoru vd. Iz čvora vd,
mrav se u čvor vs vraća
istim putem kojim je do njega došao.
Mravi u prirodi prilikom gibanja ispuštaju feromonske tragove, koji se u grafu označavaju veličinom
koja predstavlja jačinu feromonskog traga na
određenom putu (bridu) - τ.
Svaki mrav potragu za hranom započinje u čvoru vs. Sljedeći grad mrav
odabire temeljem vjerojatnosti prijelaza koja se računa prema izrazu (3.1).
|
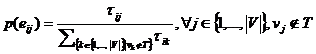
|
(3.1)
|
Što je vrijednost τ
veća, veća je i vjerojatnost da će mrav krenuti tim bridom. Na povratku iz vd u vs, mrav prolazi istim putem
kojim je već prošao, pritom ažurirajući količinu feromona
koja se veže za brid kojim mrav prolazi. Ako je mrav pošao bridom ei, količina
feromona koju ostavi na tom bridu računa se prema izrazu
(3.2), iz kojeg je vidljivo da za kraći put mrav na njemu ostavlja veću
količinu feromona i obrnuto. Ovime je implementirana
faza pojačavanja feromonskog traga.
|
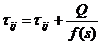
|
(3.2)
|
Ukoliko mravi dugo nisu prošli nekim bridom, feromonski trag isparava. Spomenuto ponašanje implementirano
je izrazom (3.3), pri čemu je parametar ρ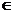 (0,1] faktor koji regulira isparavanje feromona.
(0,1] faktor koji regulira isparavanje feromona.
|
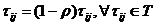
|
(3.3)
|
Iako postoje
sličnosti između prirodnih i umjetnih mrava, glavne su razlike u modelima
ponašanja sljedeće:
- Prirodni se mravi u stvarnom okruženju gibaju asinkrono, dok su
umjetni mravi sinkronizirani - u koloniju se vraćaju istim putem kojim su
do nje došli.
- Prirodni mravi konstantno ispuštaju feromone
prilikom kretanja. Umjetni mravi ispuštaju feromone
na pređeni put, ali samo prilikom povratka na početnu lokaciju.
- Evaluacija puta prirodnih mrava temelji se na činjenici kako će se
kraći putovi brže prijeći pa će feromonsko pojačanje
na njima uslijediti brže. Naprotiv, umjetni mravi evaluaciju puta
obavljaju pomoću kvalitativne mjere koja će odrediti koliko feromona trebaju ispustiti na prijeđenom putu [2].
ACO algoritam započinje fazom inicijalizacije mrava i feromonskih tragova na grafu. Svaki mrav konstruira
vlastito rješenje prolaskom od starta do cilja, a na svom povratku u koloniju
ažurira feromonski trag na prijeđenom putu
pojačavanjem feromonskog traga. Na neprijeđenom putu feromonski trag izblijedi. Nakon što je dostignut uvjet
završetka, ispisuje se najbolje rješenje [10].
|
Inicijaliziraj
populaciju mrava
Inicijaliziraj
feromonske tragove
Dok nije zadovoljen uvjet završetka
Za svakog mrava čini
Konstruiraj rješenje
Ažuriraj feromonski
trag
Pojačaj feromonski trag
Izblijedi feromonski trag
Ispiši najbolje rješenje
|
Slika 3.2 Pseudokod ACO algoritma
Ponašanje mrava,
način stvaranja rješenja problema te njegovog prikaza, ovisno je o problemu.
Funkcija cilja je
funkcija koja pridjeljuje realnu vrijednost pojedinom rješenju time ocjenjujući
njegovu dobrotu.
ACO algoritam se
zaustavlja kada je zadovoljen neki od sljedećih kriterija zaustavljanja:
·
Vremensko
ograničenje,
·
Maksimalan
broj iteracija,
·
Najbolja
vrijednost funkcije cilja nije promijenila ranije zadani broj iteracija.
U algoritmu možemo
kombinirati više kriterija zaustavljanja. Odabir najprikladnijih kriterija
zaustavljanja ovisi o problemu koji rješavamo.
Postupak
konstrukcije rješenja odnosi se na pamćenje bridova, odnosno puta kojim se mrav
kreće. Put se gradi postepeno tako da mrav zapamti brid kojim je upravo prošao
i pridoda ga skupu već prijeđenih bridova. Konačno rješenje koje je mrav
izgradio istovjetno je skupu bridova, odnosno putu koji je mrav prešao.
Mrav odlučuje kojim
bridom proći temeljem probabilističkog pravila promjene stanja. Probabilističko
pravilo promjene stanja uzima u obzir feromonske
tragove i heuristiku. Feromonski tragovi sadrže
informaciju o prethodnim dobro generiranim rješenjima čime predstavljaju
iskustvo prethodnih mrava (na dobrim su putovima mravi ostavili više feromoskog traga). Iz tog razloga količina feromonskog traga upravlja odlučivanjem mrava. Feromonski se tragovi mijenjaju dinamički tokom
pretraživanja prostora. Heuristika pomaže mravima prilikom odlučivanja tako što
im daje dodatnu informaciju o dobroti puta kojim su se kretali.
Svaki mrav ima
memoriju u kojoj pamti prijeđeni put, početno stanje i kriterij zaustavljanja [10].
3.3.6
Feromonski
tragovi
Feromonski tragovi su model koji se sastoji od τi
parametara (vrijednosti) svaki od kojih je povezan s pojedinom komponentom
rješenja (pojedinim bridom) u mravljoj okolini (grafu) [11].
Ažuriranje feromonskog traga odvija se u dvije faze: faza isparavanja
(engl. evaporation phase) i faza
pojačavanja feromona (engl.
reinforcement phase).
U fazi isparavanja, feromonski se trag gubi u odnosu na konstantnu vrijednost
parametra ρ prema izrazu (3.4).
|
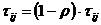
|
(3.4)
|
Parametar ρ predstavlja stopu smanjenja feromona i poprima vrijednosti iz intervala [0, 1]. Cilj
isparavanja je izbjegavanje prerane konvergencije mrava prema "dobrom"
rješenju, čime bi se onemogućilo istraživanje prostora pretraživanja.
U fazi pojačavanja, feromonski se trag ažurira u skladu s generiranim
rješenjem. U fazi pojačavanja feromonskog traga
možemo primijeniti tri strategije:
- Online korak-po-korak (engl.
online step-by-step): feromonski se trag ažurira po završetku svakog koraka
izgradnje rješenja za svakog pojedinog mrava.
- Online zakašnjelo (engl.
online delayed):
feromonski se trag ažurira nakon što mrav
izgradi vlastito rješenje.
- Offline: feromonski
se trag ažurira nakon što svi mravi izgrade vlastito rješenje. Ova je
metoda pojačavanja feromona najčešće korištena
te se u okviru nje mogu primijeniti sljedeće strategije:
- Pojačavanje temeljeno na
kvaliteti (engl. quality-based pheromone
update): feromonski
se trag pojačava na temelju najboljih k
rješenja koje je izgradilo k
mrava (k = 1,…, n, pri čemu je n broj mrava u populaciji).
Količina feromona proporcionalna je kvaliteti
rješenja.
- Pojačavanje temeljeno na rangu (engl. rank-base pheromone
update): najboljih k mrava ispušta količinu feromona
koja je proporcionalna njihovom rangu.
- Pojačavanje temeljeno na najgorem rješenju (engl.
worst pheromone update): mrav s najlošijim rješenjem smanjit će
količinu feromona na komponentama svog rješenja
tj. na putu kojim je prošao.
- Elitističko pojačavanje (engl. elitist pheromone
update): mrav s najboljim rješenjem
ažurirat će feromonski trag s ciljem pojačanja
pretrage [2].
Problem trgovačkog
putnika (engl. Travelling Salesman Problem, TSP) je NP težak problem kombinatoričke
optimizacije. U kontekstu optimizacije kolonijom mrava, TSP problem ima
značajnu ulogu zbog toga što je inicijalni ACO algoritam bio primijenjen upravo
na njemu.
Trgovački putnik
mora najkraćim mogućim putem obići sve gradove na mapi i potom se vratiti u
grad iz kojega je krenuo. Problem trgovačkog putnika se, u teoriji grafova izražava
na sljedeći način: u potpunom težinskom grafu nađi hamiltonovski
ciklus minimalne duljine. Hamiltonovski ciklus je
ciklus koji prolazi svim vrhovima grafa.
TSP problem rješava
se sustavom mrava (engl. Ant System, AS). Kako bi se sustav mrava
uspješno prilagodio za rješavanje TSP problema, u prethodno opisanoj ACO metaheuristici i modelu ponašanja umjetnih mrava potrebno
je izvršiti prilagodbe.
Problemsku okolinu
predstavit ćemo potpuno povezanim, neusmjerenim grafom G = (V, E),
pri čemu je V skup vrhova grafa
odnosno gradova kojima mrav prolazi, dok je E
skup bridova grafa G, odnosno skup udaljenosti između dva grada i i j. Prostor pretraživanja problema čine
sve kombinacije mogućih staza koje jedan mrav može načiniti u grafu G [2].
Bridovi grafa G
smatraju se komponentama rješenja. Svakom bridu, pored njegove duljine,
pridjeljujemo i jednu realnu vrijednost - parametar τ (feromonski trag). Vrijednosti feromona predstavljene su n×n matricom feromona gdje je τij količina feromonskog
traga i predstavlja poželjnost prisutnosti grane (i, j) u rješenju. Iako su svi parametri τ inicijalno postavljeni na identičnu vrijednost, njihova se
vrijednost mijenja dinamičkim ili statičkim osvježavanjem [10].
Funkcija cilja f(x) evaluira dobiveno rješenje kao sumu
udaljenosti između gradova odnosno kao sumu duljine bridova između gradova
grafa G kojim je mrav prešao kako bi stvorio dobiveno rješenje. Funkcija cilja
dobivenom rješenju dodjeljuje realnu vrijednost.
Cilj je svakog mrava
pronaći dohvatljivu stazu po grafu tj. jedno rješenje
[11]. Konstrukcija rješenja
započinje na način da mrav, slučajnim odabirom, odabere početni grad i sprema
ga u memoriju u kojoj čuva trenutno, parcijalno rješenje. Parcijalno rješenje
je rješenje koje je mrav dosad izgradio.
Slika 3.3 Algoritam optimizacije kolonijom mrava za
rješavanje problema trgovačkog putnika
Iz početnog se
grada, temeljem probabilističkog pravila mrav iterativno giba u sljedeći
dohvatljivi grad. Kada se nalazi u gradu i,
mrav k odlučuje o putovanju u sljedeći
neposjećeni grad j temeljem
vjerojatnosti
|
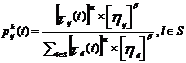
|
(3.5)
|
Svaki dohvaćani grad ponovno se sprema u memoriju kao dodatak
parcijalnom rješenju [6].
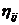 je heuristička a
priori informacija za koju vrijedi
je heuristička a
priori informacija za koju vrijedi 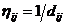 , pri čemu je dij udaljenost između gradova i i j. Motivacija ovakve heuristici
specifične informacije je dati prednost bližim gradovima. Iz tog razloga
vrijednost
, pri čemu je dij udaljenost između gradova i i j. Motivacija ovakve heuristici
specifične informacije je dati prednost bližim gradovima. Iz tog razloga
vrijednost 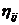 možemo smatrati
vidljivošću grada iz neke točke [3].
Što je grad udaljeniji od referentne točke, parametar
možemo smatrati
vidljivošću grada iz neke točke [3].
Što je grad udaljeniji od referentne točke, parametar 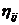 , odnosno njegova vidljivost bit će manja i obrnuto.
, odnosno njegova vidljivost bit će manja i obrnuto.
Parametri α i β koriste se kao parametri kojima se
prilagođava važnost između tragova feromona i
heurističke informacije. Povećanjem parametra α, veću prednost dajemo odabiru
putova s većom količinom feromonskih tragova [10].
Smanjimo li parametar α na nulu, ACO postaje stohastički pohlepni
algoritam i najbliži će gradovi imati veću vjerojatnost i biti izabrani [6]. Takav postupak nazivamo intenzifikacija
pretrage. Povećanjem parametra β, izbjegavamo praćenje već viđenih tragova.
Smanjenjem parametra β na nulu, vjerojatnost odabira sljedećeg grada vodit
će se samo za vrijednostima feromonskih tragova.
Prema Dorigu, ovakvim bi postupkom brzo došlo do brze
stagnacije. Prilikom stagnacije, svi mravi idu istim putem i kreiraju isto
rješenje.
Najveća vjerojatnost
prelaska u sljedeći dohvatljivi grad ne garantira da će mrav u njega i prijeći
jer se mrav ne kreće deterministički.
Posljednji posjećeni
grad mrav pamti u tabu listi i u njega se ne smije vraćati. Brid kojim je mrav
upravo prošao pamti se kao jedna od komponenta rješenja. Kada mrav posjeti
posljednji dohvatljivi grad, zatvara stazu povratkom u grad s kojeg je započeo
pretragu.
Algoritam se
nastavlja dok svaki mrav nije sagradio svoje rješenje, odnosno jednom prošao
kroz sve čvorove grafa G. U sljedećem se koraku ažuriraju feromonski
tragovi. Prva faza ažuriranja feromonskog traga je
isparavanje koje se odvija prema izrazu (3.6) [6].
|
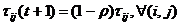
|
(3.6)
|
gdje je 0 <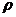
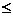 1 stopa isparavanja feromonskog
traga. Parametar
1 stopa isparavanja feromonskog
traga. Parametar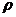 koristi se kako bi se izbjegle akumulacije feromona i njime se omogućuje „zaboravljanje“ loših putova.
koristi se kako bi se izbjegle akumulacije feromona i njime se omogućuje „zaboravljanje“ loših putova.
Pojačanje feromonskog traga izvršava se prema izrazu:
|
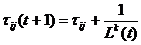 , ,
|
(3.7)
|
ako je mrav prošao
bridom (i, j).
Lk(t) je duljina puta kojeg je mrav prošao. Što je
duljina prijeđenog puta manja, na njemu će biti ispušteno više feromona.
Optimizacija rojem čestica (engl. Particle Swarm Optimisation, PSO) je stohastički optimizacijski
algoritam temeljen na populaciji rješenja. PSO pripada skupini algoritama
inteligencije roja (engl. Swarm Inteligence). Osmislili su ga
znanstvenici: James Kennedy i R. C. Eberhart 1995.
godine. Inspiraciju su pronašli u društvenom ponašanju raznih tipova organizama
poput jata ptica ili ribljih plova.
Promatranjem jata ptica, vidljivo je kako ptice mijenjaju vlastiti položaj
vođene instinktom za pronalaženjem hrane. Sve ptice u jatu traže hranu na nekom
prostoru. Postoji velika vjerojatnost da će jato slijediti onu pticu koja je
osjetila ili pronašla dobar izvor hrane. Svaka ptica pojedinačno ima instinkt
kojim želi za sebe pronaći još bolje hranilište, a kako bi to postigla,
nakratko se odvaja od jata. Pronalaskom boljeg hranilišta, pomogla je cijelom jatu
jer će je ostale ptice pratiti i preseliti se na bolje hranilište [5].
PSO kao
optimizacijsko oruđe pruža procedure za pretragu u kojoj samostalne jedinke
(agenti, potencijalna rješenja, u nastavku: čestice) mijenjaju svoju poziciju
(stanja, vrijednost rješenja problema) u vremenu.
PSO je inicijaliziran
populacijom nasumičnih rješenja - česticama koje se gibaju po
višedimenzionalnom prostoru za pretraživanje. Čestica je potencijalno rješenje
problema koje odgovara koordinatama na kojima se čestica nalazi u prostoru
pretraživanja [1]. Prostor pretraživanja je skup svih rješenja problema.
Primjerice, ako je prostor pretraživanja jednodimenzionalan, prostor
pretraživanja je skup svih točaka na x
koordinatnoj osi. Sve te točke smatramo potencijalnim rješenjima. Gibanje
čestice podrazumijeva promjenu njene pozicije tj.
koordinate u prostoru rješenja. U slučaju jednodimenzionalnog prostora
pretraživanja, čestica će se kretati mijenjanjem svoje x koordinate. Svrha kretanja čestica je što bolje istražiti prostor
pretraživanja.
Za vrijeme svake
iteracije algoritma, čestica se evaluira - određuje se njena dobrota.
Određivanje dobrote obavlja se pomoću funkcije dobrote (engl.
fitness function,
funkcija prikladnosti). Funkcija dobrote modelira se ovisno o problemu kojeg
rješavamo. Primjerice, ako tražimo optimume neke funkcije pomoću PSO algoritma,
kao funkciju dobrote koristit ćemo funkciju čiji optimum tražimo. Čestica se
evaluira tako da se njene koordinate iz prostora rješenja uvrste u funkciju
dobrote. Rezultat evaluacije je realna vrijednost koju čestica pohrani u svoju
memoriju. PSO algoritam nema spoznaju o funkciji dobrote u smislu načina kako
ona izgleda i gdje se nalaze njeni optimumi. Zbog toga PSO ne zna koliko je
čestica udaljena od optimuma kojeg traži. PSO koristi funkciju dobrote samo
kako bi vrednovao rješenja i nastavlja rad s vrijednosti koju mu funkcija
dobrote preda [1].
Za vrijeme gibanja,
svaka čestica prilagođava svoju poziciju na temelju vlastitog iskustva i na
temelju iskustva svojih susjeda. Detaljnije, svaka čestica pamti koordinate
unutar prostora pretraživanja koje predstavlja dosad najbolje rješenje te
čestice. Nazovimo tu vrijednost vlastito najbolje rješenje [5].
Čestice u roju su
susjedi. Ako su sve čestice međusobni susjedi, najbolje rješenje svih čestica u
svakoj iteraciji PSO algoritam pamti kao globalni optimum. Ako čestica ima samo
nekoliko susjeda, taj podskup čestica pamti svoj optimum kojeg zovemo lokalni
optimum. Lokalno pretraživanje ima svoje prednosti, ali i mane. Traženje
lokalnog optimuma bolje će istražiti prostor rješenja, no konvergencija
algoritma bit će sporija.
4.2
Pseudokod
|
Inicijaliziraj
parametre
Dok nije zadovoljen uvjet završetka
Za svaku česticu
Izračunaj dobrotu čestice
Ako je dobrota čestice bolja
od dotad najbolje vlastite dobrote
Ažuriraj najbolje
vlastito rješenje čestice
Ako je dobrota čestice bolja
od dotad najbolje globalne dobrote
Ažuriraj najbolje
globalno rješenje
Za svaku česticu
Ažuriraj brzinu čestice
Ažuriraj položaj čestice
|
Slika 4.1 Pseudokod algoritma PSO
Dobrota se vrednuje tako da se pozicija
čestice uvrsti u funkciju dobrote koja kao izlaz čestici daje realnu
vrijednost.
Usporedbom izračunate vrijednosti dobrote
pojedine čestice i prethodno zapamćenih vrijednosti vlastite najbolje i
globalno najbolje dobrote, po potrebi se ažuriraju vrijednosti globalnih i
vlastitih najboljih rješenja.
Roj čestica
iskorištava vektor brzine kako bi ažurirao trenutnu poziciju svake čestice u
roju. Pozicija čestice u jatu je ažurirana na temelju socijalnog ponašanja roja
koji se prilagođava svom okruženju stalnim traženjem boljih pozicija tokom
vremena.
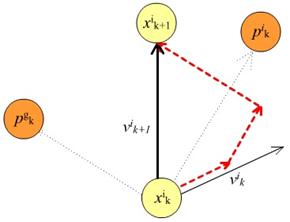
Slika 4.2 Ažuriranje pozicije čestice
Numerički, pozicija x
čestice i u iteraciji k+1 ažurira se prema izrazu (4.1).
|
 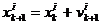
|
(4.1)
|
Vektor brzine se
ažurira na temelju pamćenja svake čestice, što koncepcijski odgovara
autobiografskoj memoriji, kao i na temelju znanja koje je stekao roj kao
cjelina.
|
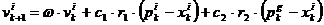
|
(4.2)
|
Pri čemu je 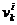 vektor brzine u
iteraciji k,
vektor brzine u
iteraciji k, 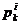 i
i 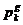 su najbolja
ikad pozicija čestice i globalna najbolja pozicija čitavog roja, sve do
trenutne iteracije k, dok r predstavlja nasumični broj iz
intervala [0, 1].
su najbolja
ikad pozicija čestice i globalna najbolja pozicija čitavog roja, sve do
trenutne iteracije k, dok r predstavlja nasumični broj iz
intervala [0, 1].
Preostali članovi su
konfiguracijski parametri koji igraju važnu ulogu u konvergencijskom ponašanju
PSO-a. Član 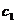 (kognitivni, samospoznajni parametar) predstavlja stupanj povjerenja u
najbolje rješenje do kojeg je došla pojedina čestica, dok član
(kognitivni, samospoznajni parametar) predstavlja stupanj povjerenja u
najbolje rješenje do kojeg je došla pojedina čestica, dok član 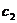 (socijalni, društveni
parametar) predstavlja stupanj povjerenja u globalno najbolje rješenje
(najbolje pronađeno rješenje od jata kao cjeline). Uglavnom se uzima 1.8 <
(socijalni, društveni
parametar) predstavlja stupanj povjerenja u globalno najbolje rješenje
(najbolje pronađeno rješenje od jata kao cjeline). Uglavnom se uzima 1.8 < 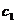 =
= 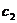 < 2.2. Parametar
< 2.2. Parametar 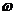 je inercijska
varijabla koja je iskorištena za kontroliranje istraživačkih sposobnosti roja
tako da skalira vrijednost trenutne brzine te na taj način utječe na iznos
ažuriranog vektora brzine. Većim vrijednostima inercijske varijable vršimo
globalno pretraživanje zbog toga što se ažurirani vektor brzine brže povećava,
dok zadavanjem manje vrijednosti inercijske varijable vrijednost ažuriranog
vektora brzine postaje manja pa se tako novi položaj čestice ograničava na
manje područje prostora istraživanja tj. omogućeno je
lokalno pretraživanje. Vrijednosti parametra
je inercijska
varijabla koja je iskorištena za kontroliranje istraživačkih sposobnosti roja
tako da skalira vrijednost trenutne brzine te na taj način utječe na iznos
ažuriranog vektora brzine. Većim vrijednostima inercijske varijable vršimo
globalno pretraživanje zbog toga što se ažurirani vektor brzine brže povećava,
dok zadavanjem manje vrijednosti inercijske varijable vrijednost ažuriranog
vektora brzine postaje manja pa se tako novi položaj čestice ograničava na
manje područje prostora istraživanja tj. omogućeno je
lokalno pretraživanje. Vrijednosti parametra 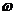 najčešće se uzimaju iz intervala
[0.8, 1.2].
najčešće se uzimaju iz intervala
[0.8, 1.2]. 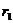 i
i 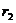 vrijednosti su iz
intervala [0, 1], koje imaju stohastičan učinak na
komponente brzine, uzrokujući polunasumično (engl. semi-random) gibanje u smjeru najboljih pronađenih rješenja
[1].
vrijednosti su iz
intervala [0, 1], koje imaju stohastičan učinak na
komponente brzine, uzrokujući polunasumično (engl. semi-random) gibanje u smjeru najboljih pronađenih rješenja
[1].
Svaka od komponenata
ažuriranja brzine imaju različitu ulogu:
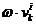 je inercijska komponenta zadužena za to
da čestica nastavi gibanje u smjeru u kojem je originalno i krenula. Manje
vrijednosti inercijske konstante ubrzavaju konvergenciju, a veće
vrijednosti potiču istraživanje prostora.
je inercijska komponenta zadužena za to
da čestica nastavi gibanje u smjeru u kojem je originalno i krenula. Manje
vrijednosti inercijske konstante ubrzavaju konvergenciju, a veće
vrijednosti potiču istraživanje prostora.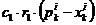 je kognitivna komponenta koja se ponaša
kao memorija čestice i usmjerava je ka mjestu u prostoru pretraživanja
gdje je postigla najbolju dobrotu.
je kognitivna komponenta koja se ponaša
kao memorija čestice i usmjerava je ka mjestu u prostoru pretraživanja
gdje je postigla najbolju dobrotu.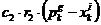 je socijalna komponenta koja usmjerava
česticu ka mjestu u prostoru pretraživanja gdje je roj pronašao najbolje
rješenje [1][12].
je socijalna komponenta koja usmjerava
česticu ka mjestu u prostoru pretraživanja gdje je roj pronašao najbolje
rješenje [1][12].
Animacija je slijedni prikaz dvodimenzionalnih ili
trodimenzionalnih ilustracija, slika ili modela čijom se brzo izmjenom, zbog perzistencije vida, stvara optička iluzija pokreta.
Animacije se koriste kada se neki sadržaj želi
prikazati dinamički. U suprotnosti sa statičkim slikama, animacijama se
promjene na ekranu mogu prikazati pomakom ili transformacijom nekog objekta u
stvarnom vremenu. Ilustracije radi, objekte statičke slike ne možemo micati pa
se pokret na njima predočava tako da na sliku dodamo strelice koje
demonstriraju smjer gibanja.
U animaciji naprotiv, slikama se može mijenjati
pozicija ili ih se može transformirati što animacije čini idealnima za prikaz
raznih procesa ili procedura. Animacijama dobivamo življi, privlačniji i
razumljiviji edukativni materijal.
Svrha animacije je osposobiti studenta za primjenu algoritama inteligencije
roja na različitim problemima optimizacije.
Animacija je namijenjena profesorima fakulteta računarstva koji animaciju
mogu koristiti kao nastavno pomagalo, studentima računarskih smjerova koji
animaciju mogu koristiti kao popratni materijal prilikom učenja i programiranja,
te nastavnicima i učenicima srednjih škola i gimnazija koji žele obogatiti
nastavni sadržaj. Animacija se može koristiti kao pomagalo za korištenje u
nastavi i kao pomoć pri učenju.
S obzirom na to da je jezik tekstualnih objašnjenja hrvatski, ciljana
skupina polaznika obuhvaća osobe hrvatskog govornog područja.
Kako bi učenje korisnika bilo što efektivnije, definiraju se sljedeći
ishodi učenja. Nakon proučavanja animacije polaznici će moći:
·
Opisati način rada genetskog
algoritma
·
Nabrojati genetske operatore
·
Načiniti podjelu operatora selekcije
i nabrojati podvrste selekcije
·
Nabrojati podvrste križanja i
mutacije
·
Opisati ponašanje svakog genetskog
operatora
·
Primijeniti genetski algoritam na
problemu minimizacije funkcije
·
Opisati način rada algoritma
optimizacije kolonijom mrava
·
Primijeniti algoritam optimizacije
kolonijom mrava za rješavanje problema trgovačkog putnika
·
Opisati način rada algoritma
optimizacije kolonijom mrava
·
Opisati način rada algoritma
optimizacije rojem čestica
·
Opisati gibanje čestice u ovisnosti o
vektorima položaja i brzine
·
Primijeniti algoritam optimizacije
rojem čestica na problem minimizacije funkcije.
Konceptualna mapa je grafički prikaz sadržaja koji pokazuje
kako su povezane informacije koje učenici/studenti trebaju naučiti. Prikaz
konceptualne mape mora odražavati ishode učenja i svrhu animacije.
Konceptualna mapa na slici 5.1 pokazuje koji su dijelovi
animacije međusobno povezani kako bi se studentima olakšalo praćenje gradiva (navigacija
unutar sustava).
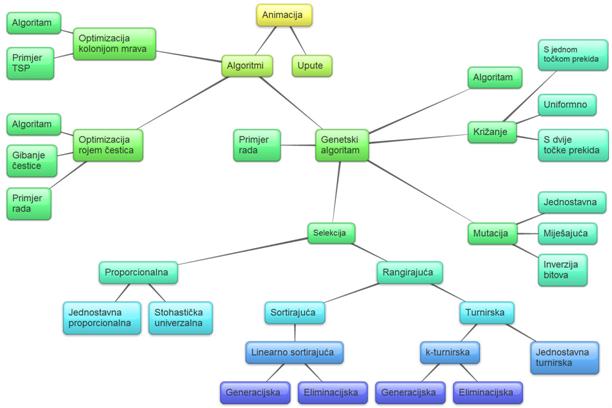
Slika 5.1 Konceptualna mapa izrađene animacije
Osim povezanosti, konceptualna mapa ujedno je i prikaz
implementiranih podanimacija. Svaki krajnji list
nekog čvora jedna je podanimacija.
Animacija je izrađena
u programu Adobe Flash
Professional CS5.5. Kako bi se animacija mogla pokrenuti lokalno na
računalu, korisnik mora imati instaliran Adobeov Flash Player
verziju 10.2 ili veću, te miš i tipkovnicu. Ukoliko se aplikaciji pristupa
putem Interneta, na računalu je potrebno imati instaliran Internet preglednik.
Prije nego se animacija pokrene, na prozor animacije potrebno je kliknuti
mišem. Navedena se akcija mora izvršiti kako bi se izbjeglo automatsko
pokretanje animacije (engl. autoplay) prije nego je scena u
cijelosti učitana. Spomenuti je problem osobito izražen ako se animaciji
pristupa preko web sučelja.
Upute za navigaciju kroz simulaciju nalaze se na početnom zaslonu
animacije, a u bilo kojem im je trenutku moguće pristupiti kroz glavni
izbornik. Opis funkcionalnosti glavnog izbornika nalazi se u podpoglavlju 5.2.6.
Kroz animaciju se moguće kretati pomoću miša i tipkovnice. Pomoću miša,
pritiskom na odgovarajuće gumbe glavnog izbornika, a pomoću tipkovnice pritiskom
na tipke navedene u Tablica 5.1.
Tablica 5.1 Upute za navigaciju kroz animaciju
|
TIPKA
|
FUNKCIONALNOST
|
|
M
|
Otvaranje
glavnog izbornika
Zatvaranje glavnog izbornika
|
|
ESC
|
Zatvaranje
glavnog izbornika
|
|
STRELICA LIJEVO
|
Ponovi prethodni
korak
|
|
STRELICA DESNO
|
Pomak na
sljedeći korak
|
|
R
|
Ponovi scenu
|
|
ENTER
|
Sljedeća scena
|
Temelj svake Flash animacije je vremenski
slijed (engl. timeline). Pomoću vremenskog slijeda, animacija se može
izraditi kao niz okvira (engl. frame). U svakome od okvira nalazit
će se jedna sličica. Prikaz okvira u nizu tvori animaciju.
|
Slika 5.2 Struktura Flash animacije
|
|
 
|
Više okvira čini sloj. Sloj je nevidljiva ploha koja se nalazi između
korisnika i pozornice. Svaki objekt kojeg stavljamo na pozornicu (engl. stage) mora se smjestiti u poseban sloj ako ga želimo
pomicati po sceni neovisno o drugim elementima. Statički elementi mogu se
smjestiti u jedan sloj. Slojevi su u vremenskom slijedu prikazani jedan ispod
drugog. Najviši sloj najbliži je korisniku.
Vremenski slijed može se sastojati od više slojeva. Ako su srodni,
slojevi se mogu grupirati u direktorije (engl. directory) (slika
5.2).

Slika 5.3 Skica organizacije scene algoritma križanja s
dvije točke prekida
Ako se neki objekt
želi pokretati po sceni, potrebno ga je smjestiti u zaseban sloj i potom načiniti
animaciju međupokreta. Postoje tri vrste međupokreta:
- Klasična animacija međupokreta
(engl. Classsic Tween) - pomoću ove opcije definira se kretanje
između dvije točke. U početnom i završnom okviru kretanja postavlja se
početna i završna točka kretanja. Flash potom samostalno proračuna sve međukorake i ucrta
ih u primjerene okvire. Objekt se giba pravocrtnim gibanjem.
- Objekt se može gibati i po zadanoj
nacrtanoj putanji (engl. Motion Tween).
Vodilica pokreta (engl. Motion Guide) pomoćni je sloj u koji se
smješta putanja nekog simbola. Svaka vodilica pokreta može imati samo
jednu putanju, no na jednoj se putanji može kretati više objekata.
- Animacija
međuoblika (engl. Shape Tween)
provodi se nad vektorski definiranim objektima na način da se objekt
transformira iz početnog oblika u konačni oblik matematičkim proračunima.
5.2.3
ActionScript
3
ActionScript 3 je objektno orijentiran programski
jezik (sličan JavaScriptu)
koji služi za dodavanje interaktivnosti animacijama.
Akcije se mogu definirati u okvirima vremenskog
slijeda, na gumbima te na animiranim simbolima. Pri definiranju akcije,
potrebno je odrediti kada će se akcija dogoditi, odnosno što će izazvati tu
akciju (klik mišem, pritisak na tipku tipkovnice) te što će se dogoditi
aktiviranjem akcije.
|
selProp_btn.addEventListener(MouseEvent.CLICK,
selPropExpand);
function selPropExpand(evt:MouseEvent):void{
gotoAndStop("proporcionalnaExpand");
}
|
Slika 5.4 Dio ActionScript
koda iz animacije
Na slici 5.4 prikazan je dio ActionScript 3 koda. Crvenom je bojom označeno ime gumba nad kojim se definira
akcija. Funkcija addEventListener
"osluškuje" odnosno čeka da se definirana akcija dogodi. U ovom će se
slučaju akcija provesti klikom na lijevu tipku miša. Akcija se definira
vlastitom definiranom funkcijom selPropExpand.
Slika 5.5 Organizacije pozornice Flash
animacije
Pozornica (engl. stage) vidljivi je dio Flash animacije na kojeg je
moguće smjestiti proizvoljan broj animacijskih elemenata: animirane simbole,
gumbe i grafičke elemente (slika 5.5). Sva kretanja elemenata vidljiva su samo
u okviru prozora pozornice čije dimenzije je moguće zadati i promijeniti tokom
izrade animacije.
Svaka se scena u izrađenoj animaciji sastoji od sljedećih komponenata:
naslov, platno za simulaciju, simulacija, ploča za popratni tekst, popratni
tekst, glavni izbornik te pozadina.
Motivacija dizajna animacije prikazanog na slici 5.6 nalazi se u primjeni
animacije na nastavi - scene se odvijaju na kino platnu, a objašnjenja se
ispisu na pozadini školske ploče.
Dimenzija scene postavljena je na 800*650 piksela.

Slika 5.6 Dizajn izrađene animacije
O ovom će odjeljku
biti opisana funkcionalnost pojedinih elemenata animacije.
Glavni izbornik temeljni je navigacijski element animacije.

Slika 5.7 Gumbi glavnog izbornika
Na slici 5.7 prikazani su gumbi kojima se omogućuje navigacija kroz
simulaciju. Klikom na gumbe može se ponoviti scena, skočiti na sljedeću scenu,
ponoviti ili ubrzati korak simulacije, vratiti se na glavni izbornik ili dobiti
pristup uputama o navigaciji kroz animaciju. Osim što gumbi mijenjaju boju
(gradijent se linearno invertira) prelaskom pokazivačem miša preko njih, tekst
koji opisuje akciju gumba prikazuje se ispod gumba (slika 5.8). Glavni izbornik
se gasi pritiskom na gumb X u gornjem lijevom uglu izbornika.

Slika 5.8 Glavni izbornik
Otvaranje i zatvaranje izbornika animira se klasičnim međupokretom
(engl. classic tween).
Glavni izbornik organiziran je kao animirani simbol (engl.
movie clip) koji se
sastoji od gumba za  otvaranje/zatvaranje
izbornika, gumbi za manipulaciju animacijom i grafičkih elemenata koji se
prikazuju iznad gumbi te tekstualnog okvira koji prikazuje dinamički tekst (slika
5.8).
otvaranje/zatvaranje
izbornika, gumbi za manipulaciju animacijom i grafičkih elemenata koji se
prikazuju iznad gumbi te tekstualnog okvira koji prikazuje dinamički tekst (slika
5.8).
Nad svakim se gumbom postavlja osluškivač
događaja (engl. event listener) kojim se definira što koji
gumb radi na definiranu akciju.
|
restartScene_btn.addEventListener(MouseEvent.ROLL_OVER,
restartScene);
function restartScene(event:MouseEvent):void{
tekst.text =
"Ponovi scenu";
}
restartScene_btn.addEventListener(MouseEvent.CLICK,
restartScene1);
function restartScene1(event:MouseEvent):void
{
if( MovieClip(root).currentLabel == "jednPropSel"
)
MovieClip(root).jednPropSel_mc.gotoAndPlay("start");
}
restartScene_btn.addEventListener(MouseEvent.ROLL_OUT,
blankStatusText);
function blankStatusText(event:MouseEvent):void{
tekst.text =
"";
}
|
Slika 5.10 Isječak koda glavnog izbornika
U ovom su radu načinjene
animacije koje prikazuju rad sljedećih algoritama:
·
Jednostavna
proporcionalna selekcija
·
Stohastička
univerzalna selekcija
·
Linerarno sortirajuća selekcija (generacijska i eliminacijska)
·
k-turnirska (generacijska i eliminacijska)
·
Jednostavna
turnirska selekcija
·
Jednostavna
mutacija
·
Miješajuća
mutacija
·
Mutacija
inverzijom bitova
·
Križanje s
jednom i dvije točke prekida
·
Uniformno
križanje.
U nastavku su opisani
scenariji svake od scena.
Jednostavna
proporcionalna selekcija je oblik selekcije u kojoj se temeljem kvocijenta
dobrote jedinke i ukupne dobrote svih jedinki određuje vjerojatnost s kojom će
jedinka biti odabrana. Potom se generira nasumični broj r iz intervala [0, 1]. Ako se vrijednost r nalazi u granicama kumulativne dobrote jedinke j, jedinka j bit će kopirana u međupopulaciju. Iz
populacije se odabire N jedinki, pri
čemu je N veličina populacije
jedinki.
Slika 5.11 Skica animacije jednostavne proporcionalne
selekcije
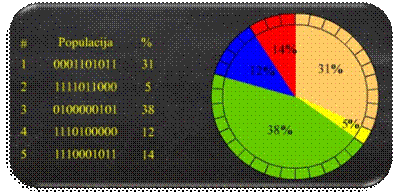
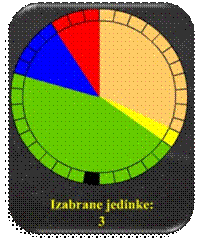
Zbog načina odabira
jedinki, konstruiranje jednostavne proporcionalne selekcije često se uspoređuje
s kotačem ruleta koji se generira temeljem vjerojatnosti odabira pojedinih
jedinki (slika 5.11.a). Kotač se "zavrti" i nasumično zaustavlja N puta. Jedinka na kojoj se zaustavlja
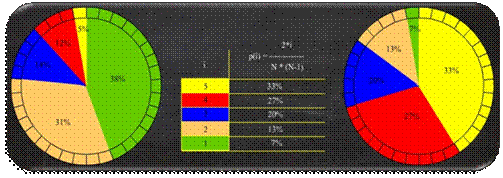
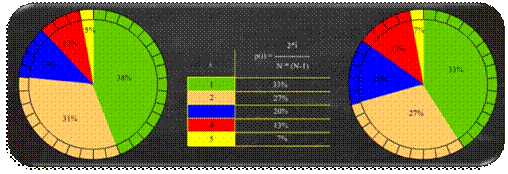
značka stavlja se u međupopulaciju P'(t) (slike 5.11.b i 5.11.c).
Stohastička
univerzalna selekcija, na temelju iste raspodjele vjerojatnosti kao i
jednostavna proporcionalna selekcija stvara kotač ruleta (slika 5.12.a). Kotač
se podijeli na N intervala (N je veličina populacije). Na rub svakog
intervala stavlja se značka (slika 5.12.b). Jedinka ispod značke kopira se u međupopulaciju (slika 5.12.c).
Slika 5.12 Skica animacije stohastičke univerzalne
selekcije
5.3.3
Linerano sortirajuća selekcija
Linearno sortirajuća
selekcija je rangirajuća selekcija kod koje je
vjerojatnost selekcije jedinke veća što je bolji položaj jedinke u poretku po
dobroti.
Razlikujemo generacijsku (slika 5.13.a)
i eliminacijsku linearno sortirajuću selekciju (slika
5.13.b). Navedena dva tipa selekcije razlikujemo po položaju najbolje i
najlošije jedinke u populaciji. Tako će u generacijskoj selekciji najbolja
jedinka biti ona s indeksom N, a
najgora ona s indeksom 1. Naprotiv, u eliminacijskom će algoritmu najbolja
jedinka biti ona s indeksom 1, a najgora će biti jedinka s indeksom N.
|
a)
|
|
b)
|
Slika 5.13 Skica animacije linearno sortirajuće
selekcije
K-turnirska
generacijska selekcija je rangirajuća selekcija kod
koje se u svakoj iteraciji odabire k
jedinki (slika 5.14.b) iz populacije P(t)
(slika 5.14.a) koje se potom rangiraju tj. sortiraju
po vrijednosti funkcije dobrote (slika 5.14.d). Jedinka s najvećom vrijednosti
funkcije dobrote kopira se u međupopulaciju P'(t) (slika 5.14.e). Postupak se ponavlja N puta dok se ne izgradi cijela međupopulacija veličine N
(slika 5.14.b).
Slika 5.14 Skica animacije k-turnirske generacijske
selekcije
K-turnirska
eliminacijska selekcija je rangirajuća selekcija kod
koje se u svakoj iteraciji odabire k
jedinki (slika 5.15.b) iz populacije P(t)
(slika 5.15.a) koje se potom rangiraju tj. sortiraju
po vrijednosti funkcije dobrote (slika 5.15.b). Jedinka s najmanjom vrijednosti
funkcije dobrote eliminira se u populaciji P(t) (slika 5.15.c), a preostale se jedinke križaju i mutiraju.
Njihova djeca zamjenjuju eliminirane jedinke (slika 5.15.d). Postupak se
ponavlja dok ne bude zadovoljen uvjet završetka.
Slika 5.15 Skica animacije k-turnirske eliminacijske
selekcije
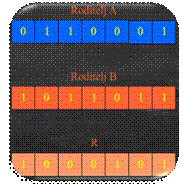
Postupak jednostavne
turnirske eliminacijske selekcije prikazan je na slici 5.16. Iz populacije P(t) odabere se jedan par jedinki (slika
5.16.b). Lošiju jedinku eliminiramo iz populacije. Potom se od preostalih
jedinki odabire novi par jedinki, pri čemu se lošija jedinka također eliminira
(slika 5.16.c). Dvije izabrane jedinke podvrgnemo križanju, mutaciji i
evaluaciji (slika 5.16.d). Dobivena djeca zamjenjuju eliminirane jedinke u
populaciji P(t) (slika 5.16.e).
Slika 5.16 Skica animacije jednostavne turnirske
eliminacijske selekcije
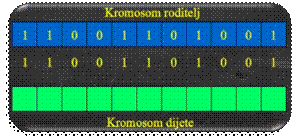
Križanje s jednom
točkom prekida oblik je križanja kod kojeg se genetski materijal izmjenjuje u
ovisnosti o poziciji točke prekida.
Slika 5.17 Skica animacije križanja s jednom točkom
prekida
Dva se binarna
kromosoma (slika 5.17.a) rastavljaju u ovisnosti o nasumično generiranoj točki
prekida (točku prekida predstavlja strelica, slika 5.17.b). Genetski se materijal
izmjenjuje (slika 5.17.c), a novonastali se kromosomi (slika 5.17.d) vraćaju u
populaciju.
Križanje s dvije točke
prekida oblik je križanja kod kojeg se genetski materijal izmjenjuje u
ovisnosti o pozicijama dvije točke prekida.
Slika 5.18 Skica animacije jednostavne turnirske
eliminacijske selekcije
Dva se binarna
kromosoma (slika 5.18.a) rastavljaju u ovisnosti o nasumično generiranim točkama
prekida koje u animaciji predstavljaju strelice (slika 5.18.b). Genetski se materijal
izmjenjuje (slika 5.18.c), a novonastali se kromosomi (slika 5.18.d) vraćaju u
populaciju.
Uniformno križanje je
vrsta križanja kod koje se geni iz roditelja kopiraju u ovisnosti o nasumično
generiranom vektoru R. Ukoliko se generira prvo dijete, a vrijednost gena u
kromosomu R je nula, u dijete će se na istoj poziciji kopirati gen prvog
roditelja. U protivnom, ako je vrijednost gena u kromosomu R jedan u dijete će
se kopirati gen drugog roditelja.
Drugi način
ostvarivanja uniformnog križanja je da se vrijednost gena kromosoma djeteta
računa prema aritmetičkoj operaciji.
Slika 5.19 Skica animacije uniformnog križanja
Na slici 5.19
prikazana je animacija uniformnog križanja koja na temelju dva kromosoma
roditelja (slika 5.19.a) generira kromosom dijeteta
na način da računa vrijednost gena djeteta na poziciji i prema aritmetičkom izrazu u koju se uvrštavaju geni oba roditelja
na poziciji i (slika 5.19.b).
Inverzija bitova je
oblik mutacije koji djeluje nad pojedinim ili svim genima kromosoma tako da mijenja
trenutnu vrijednost gena u recipročnu (0 u 1 i 1 u 0).
Slika 5.20 Skica animacije mutacije inverzijom bitova
Kromosom roditelj je
binarni kromosom koji se sastoji od 11 bitova (slika 5.20.a). Nakon provedbe
mutacije s inverzijom bitova (slika 5.20.b), sve su vrijednosti gena na istim
pozicijama u novonastalom kromosomu recipročne onima iz roditeljskog kromosoma
(slika 5.20.c).
Miješajuća mutacija
oblik je mutacije koja se provodi nad svim genima kromosoma na način da se
izmiješaju svi geni. Trenutna pozicija gena u roditeljskom kromosomu zamjenjuje
se drugom pozicijom.
Slika 5.21 Skica animacije miješajuće mutacije
Za prikaz roditeljskog
kromosoma koristi se binarni prikaz s 11 gena (slika 5.21.a). Broj nula i
jedinica u kromosomu ostaje nepromijenjen nakon djelovanja miješajuće mutacije
jer se nisu generirali novi geni (slika 5.21.b). Postojećim je genima samo
promijenjena pozicija u kromosomu - izmiješani su (slika 5.21.c).
Jednostavna mutacija
je oblik mutacije kod koje se za svaki gen u kromosomu određuje hoće li doći do
mutacija ili neće, u ovisnosti o vjerojatnosti mutacije pm.
|
a) 
|
|
b) 
|
Slika 5.22 Skica animacije jednostavne mutacije
Za svaki gen kromosoma
roditelja (binarni kromosom duljine 19 bitova, slika 5.22.a) ispituje se nalazi
li se nasumično generirani broj r iz
intervala [0, 1] u vjerojatnosnom intervalu mutacije
[0, p_m] (slika 5.22.b). Ukoliko se
broj r nalazi u intervalu [0, p_m], ispitni će gen mutirati.
5.4.1
Minimizacija
funkcije genetskim algoritmom
U animaciji je implementirana prva iteracija postupka minimizacije funkcije
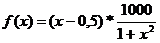 .
.
U algoritmu je korištena 3-turnirska eliminacijska
selekcija, uniformno križanje i jednostavna mutacija. U tablici 5.2. prikazane
su vrijednosti jedinki nakon prve iteracije. Na slici 5.23 prikazan je dio
animacije u kojem se inicijaliziraju jedinke.
Tablica
5.2 Prikaz rada GA u prvoj iteraciji prije
križanja i mutacije jedinki
|
Jedinka
|
b
|
x
|
f(x)
|
pomak
|
sortiranje
|
|
11010111
|
215
|
137.25
|
7.3
|
444.2
|
7
|
|
01011001
|
89
|
-60.39
|
-16.7
|
420.3
|
4
|
|
11101111
|
239
|
174.9
|
5.7
|
442.7
|
6
|
|
01011011
|
91
|
-57.25
|
-17.6
|
419.3
|
3
|
|
10111000
|
184
|
88.63
|
11.2
|
448.2
|
9
|
|
00110100
|
52
|
-118.43
|
-8.5
|
428.5
|
5
|
|
01111110
|
126
|
-2.35
|
-436.9
|
0
|
1
|
|
11001011
|
203
|
118.43
|
8.4
|
445.4
|
8
|
|
10010101
|
149
|
33.73
|
29.2
|
466.1
|
10
|
|
01101100
|
108
|
-30.59
|
-33.2
|
403.8
|
2
|
U populaciji se nalazi desetak jedinki. Jedinke su prikazane
binarnim prikazom. Vrijednosti pojedinih bitova su statične i generirane su
nasumično. Duljina svake jedinke iznosi osam bitova. Algoritam započinje
postupkom dekodiranja u kojem se iz binarnih vrijednosti kromosoma određuje
dekadska vrijednost b, a potom i
realna vrijednost x. Realna
vrijednost x uvrštava se u izraz
funkcije cilja f(x). Kako vrijednost
funkcije cilja ne smije biti negativna, nad jedinkama se provodi postupak
pomaka odnosno translacije. Jedinke se potom sortiraju po rastućoj vrijednosti
dobivenoj nakon pomaka.
Postupkom 3-turnirske eliminacijske selekcije, slučajnim se
postupkom odabiru tri jedinke. Odabiru se jedinke koje u sortiranom nizu imaju
oznake 1, 2 i 4. Jedinka 4 se eliminira jer ima najveću vrijednost funkcije
cilja.
Nad jedinkama s oznakama 1 i 2 provodi se uniformno križanje
s vjerojatnošću p = 0.5. Križanjem
nastaje nova jedinka 01101110. Jednostavnom mutacijom (p=0.5) mijenja se drugi bit. Nova jedinka ima strukturu 01101010.
Po evaluaciji jedinke, ona se vraća u početnu populaciju na mjesto eliminirane
jedinke.
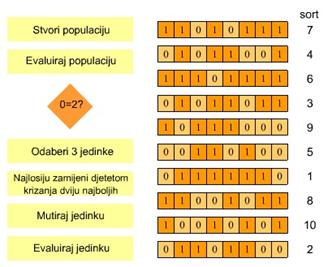
Slika 5.23 Prikaz populacije nakon sortiranja
Algoritam optimizacije kolonijom mrava u animaciji je
predočen pri rješavanju problema trgovačkog putnika (slika 5.24.a).
Kolonija od tri mrava traži najkraću udaljenost između
četiri grada. Svaki mrav u listi pamti koje je gradove posjetio, kako se u njih
ne bi vraćao te listu gradova koje smije posjetiti. Pored njih, pamti se i
trenutna pređena udaljenost između gradova. Gradovi se odabiru temeljem
probabilističkog pravila.
Po završetku svih obilazaka, ažuriraju se feromonski tragovi (slika 5.24.b). Feromonski
su tragovi prikazani matrično.
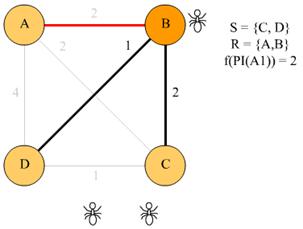
a)
|
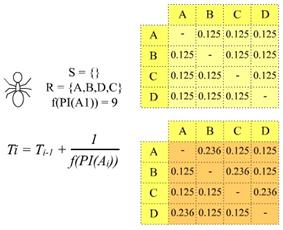
b)
|
Slika 5.24 Optimizacija kolonijom mrava
5.4.3
Minimizacija
funkcije optimizacijom rojem čestica
U animaciji je implementiran postupak minimizacije
funkcije 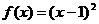 pomoću PSO algoritma
optimizacije rojem čestica (slika 5.25).
pomoću PSO algoritma
optimizacije rojem čestica (slika 5.25).
|
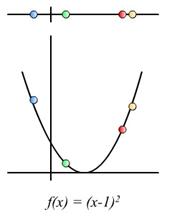
a)
|

b)
|
Slika 5.25 Animacija PSO primjera
Svaka jedinka pamti vlastiti položaj, brzinu, dobrotu i
vlastito najbolje rješenje, dok se u algoritmu pamti najbolje rješenje svih
jedinki.
U animaciji se u svakoj iteraciji jedinke prikazuju na dva
grafa (slika 5.25.a). Jedan graf prikazuje jedinke u prostoru pretraživanja,
dok se u drugom jedinke mapiraju na funkciju čiji
minimum tražimo kako bi se mogla očitati vrijednost funkcije cilja svake
jedinke. Po završetku svake iteracije, jedinke ažuriraju svoje pozicije (slika
5.25.b) i vrijednosti brzine.
Veličina populacije ograničena je na četiri jedinke, a
parametri inercije i spoznajni faktori postavljeni su na vrijednost 1. Temeljem
tih ograničenja, vrijednosti jedinke u svim iteracijama prikazane su u tablici
5.3.
Tablica
5.3 Rezultati PSO algoritma za minimizaciju funkcije po česticama i iteracijama
|
Jedinka
|
|
1. iteracija
|
2. iteracija
|
3. iteracija
|
4. iteracija
|
|
1.
|
x
|
2.2
|
0.5
|
-0.9
|
1
|
|
v
|
0.1
|
-1.7
|
-1.4
|
1.9
|
|
f(x)
|
1.44
|
0.25
|
3.61
|
0
|
|
p_best
|
2.2
|
0.5
|
0.5
|
1
|
|
2.
|
x
|
-0.6
|
0.6
|
2
|
1
|
|
v
|
0.2
|
1.2
|
1.4
|
-1
|
|
f(x)
|
2.56
|
0.16
|
1
|
0
|
|
p_best
|
-0.6
|
0.6
|
0.6
|
1
|
|
3.
|
x
|
0.4
|
0.6
|
1
|
1.4
|
|
v
|
0.2
|
0.2
|
0.4
|
0.4
|
|
f(x)
|
0.36
|
0.16
|
0
|
0.16
|
|
p_best
|
0.4
|
0.6
|
1
|
1
|
|
4.
|
x
|
2.5
|
0.8
|
-0.9
|
1
|
|
v
|
0.4
|
-1.7
|
-1.7
|
1.9
|
|
f(x)
|
2.25
|
0.04
|
3.61
|
0
|
|
p_best
|
2.5
|
0.8
|
0.8
|
1
|
|
g_best
|
-
|
0.4
|
0.8
|
1
|
Algoritmi zasnovani na evolucijskom računanju koriste se na
širokom spektru optimizacijskih problema. Različiti problemi optimizacije
zahtjeva uporabu drukčijih algoritama i operatora pretraživanja. Evolucijski
algoritmi temeljeni su na heuristikama. Znanje kojeg posjeduju jedinke,
ugrađeno je u način prikaza jedinke. U programima se najčešće koristi binarni
prikaz jednostavnosti manipulacije takvim objektima.
U sklopu rada načinjena je Flash animacija kojom se pokazuje
rad genetskog algoritma (GA), algoritma optimizacije kolonijom mrava (ACO) i
algoritma optimizacije rojem čestica (PSO). Posebna je pažnja usmjerena na
implementaciju operatora genetskog algoritma - selekciju, mutaciju i križanje.
Implementirana je jednostavna
proporcionalna selekcija, stohastička univerzalna selekcija, linearno sortirajuća selekcija (generacijska i eliminacijska),
k-turnirska (generacijska i eliminacijska), jednostavna turnirska selekcija,
jednostavna mutacija, miješajuća mutacija, mutacija inverzijom bitova, križanje
s jednom i dvije točke prekida, uniformno križanje. Pored toga implementiran je
način rada genetskog algoritma, te primjer prve iteracije minimizacije
funkcije na populaciji od 10 jedinki.
Algoritam optimizacije
kolonijom mrava implementiran je na primjeru prve iteracije problema trgovačkog
putnika koji nalazi najkraći put između četiri grada. Pored navedenih,
implementiran je i način rada algoritma optimizacije rojem čestica, translacija
čestice u ovisnosti o vektorima brzine i položaja, te primjer minimizacije funkcije pomoću populacije čestica od četiri
jedinke.
Načinjeno je i grafičko sučelje koje povezuje sve implementirane
algoritme. Grafičko sučelje obuhvaća naslov animacije, glavni izbornik koji
služi za navigaciju kroz scene animacije, te prozor s opisom rada pojedinog
algoritma koji se trenutno prikazuje na glavnom zaslonu.
Zbog Flash
tehnologije u kojoj je načinjena, implementirana je animacija portabilna i može
se koristiti lokalno na računalu ili putem weba, ako je na korisničkom računalu
instaliran Adobeov Flash Player.
Pomoću izrađene Flash animacije studenta se priprema
za primjenu algoritama inteligencije roja na različitim problemima
optimizacije. Flash animacija koristan je
način prikaza rada algoritama temeljenih na evolucijskom računanju jer autoru
ostavlja nebrojene mogućnosti prikaza rada algoritama. Također, Flash animacija je dobra tehnika prikaza rada jer zahtijeva
minimalne tehnološke uvjete (računalo, miš i tipkovnicu), a može se objaviti i
na Internetu čime joj se omogućava pristup s bilo koje lokacije koja ima
pristup Internetu.
[1] Blondin,, J. Particle Swarm Optimization Tutorial,2009.
Preuzeto 1.5.2012. s http://cs.armstrong.edu/saad/csci8100/pso_tutorial.pdf
[2] Blum, C., Ant colony optimization:
Introduction and recent trends, Physics of
Life Reviews
2 (2005) 353–373, Science Direct,
preuzeto 16.4.2012 s http://www.ie.metu.edu.tr/~ie505/CourseMaterial/Blum%20%282005%29.pdf
[3] Bronić, T., Optimizacija kolonijom mrava, Sveučilište
u Zagrebu, Zagreb, 2008. Preuzeto
14.3.2012. s http://www.zemris.fer.hr/~golub/ga/studenti/projekt2008/aco/
TomislavBronic_ACO.pdf
[4] Chakraborty, R., Fundementals of Genetic Algorithms: AI course lecture 39-40, notes, slides. 2010. Preuzeto 3.5.2012. s http://www.myreaders.info/09_Genetic_
Algorithms.pdf
[5] Domović, D., Optimizacija
rojem čestica, Sveučilište u Zagrebu, Zagreb, 2008. Preuzeto 14.3.2012. s http://www.zemris.fer.hr/~golub/ga/studenti/projekt2008/ pso/Projekt.pdf
[6] Dorigo,
M., Stützle, T. The Ant Colony Optimization
Metaheuristic: Algorithms, Applications, and Advances, preuzeto
16.3.2012. s http://code.ulb.ac.be/dbfiles/ DorStu2002MetaHandBook.pdf
[7] Jakobović, D. Genetski algoritam - predavanje. Sveučilište u Zagrebu. 2010. Preuzeto 20.5.2012. s http://www.fer.hr/_download/repository/ GApredavanje.pdf
[8] Golub, M. Genetski algoritam, prvi
dio (skripta). Sveučilište u Zagrebu. 2010., Preuzeto 10.2.2012. s http://www.zemris.fer.hr/~golub/ga/ga_skripta1.pdf
[9] Golub, M. Genetski algoritam, drugi
dio (skripta). Sveučilište u Zagrebu. 2004., Preuzeto 10.2.2012. s http://www.zemris.fer.hr/~golub/ga/ga_skripta2.pdf
[10] Skorin-Kapov, N. Heuristicke Metode Optimizacije: Optimizacija kolonijom
mrava, predavanja. Sveučilište
u Zagrebu, 2012. Preuzeto 18.3.2012. s http://www.fer.unizg.hr/_download/repository/Predavanje_11_%5BHR%5D_- _Optimizacija_kolonijom_mrava.pdf
[11] Talbi, E. Metaheuristics from design to implementation, John
Wiley & Sons, Inc., 2009.,
New Yerrsey
[12] Umarani, R., Selvi, V. particle swarm optimization - evolution, overview and applications. International Journal of Engineering
Science and Technology Vol. 2(7),
2010, 2802-2806, preuzeto 1.5.2012. s http://www.ijest.info/docs/IJEST10- 02-07- 66.pdf
[13] Wikipedia
- Genetic Algorithm. Genetic Algorithm. Preuzeto
16.5.2012. s http://en.wikipedia.org/wiki/Genetic_algorithm
![]()
![]()
![]() ABSTRACT
ABSTRACT![]() KLJUČNE RIJEČI, KEYWORDS
KLJUČNE RIJEČI, KEYWORDS