1. Uvod

Genetski algoritmi sve više dolaze do izražaja kao učinkovite metode za rješavanje raznih klasa problema. Na početku su to bili optimizacijski problemi, no kao što se vidi iz radova predstavljenih u poglavlju dva područja primjene znatno su šira. Razlog tome leži u prilagodljivosti genetskog algoritma problemu, što mu je i najveća prednost, ali i najveća mana. Mana zbog toga, jer se za svaki tip problema mora razviti genetski algoritam koji ga rješava ili se problem mora prilagoditi nekom postojećem genetskom algoritmu.

Genetski algoritmi su toliko napredovali da su u nekim primjenama postali i bolji od čovjeka. Jedan dobar primjer za to je razvoj turbine za Boeing 777, gdje su genetski algoritmi napravili i bolje rješenje i znatno su skratili vrijeme izrade proizvoda.

Kao što im samo ime kaže svoje principe temelje na teoriji evolucije. Iz populacije jedinki, bolje jednike opstaju i tako se kroz određeni broj generacija dolazi do sve boljeg rješenja, tj. sve se više rješenje približava optimumu. Do toga se dolazi korištenjem operatora križanja i mutacije. Operatori križanja su operatori koji uzimaju genetski materijal roditeljia i pomoću njega formiraju djecu, dok je operator mutacije operator koji najćešće služi kako bi unio raznolikost u populaciju, odnosno izbjegao eventualno zaglavljivanje algoritma u nekom lokalnom optimumu do kojeg bi se moglo doći samo križanjem. No kao što se vidi iz poglavlja tri moguće je baš i suprotno, da operator mutacije može pasti u lokalni optimum, a operator križanja je tu da ga spriječi u tome i vrati na pravi put. Bitno je još spomenuti da su genetski algoritmi spora metoda za pronalaženje rješenja, ali zbog načina na koji rade relativno brzo mogu proizvesti dobro rješenje.

Zbog toga se sve više napora ulaže u kombiniranje genetskih algoritama s drugim tehnikama za rješavanje problema kako bi se brže i učinkovitije došlo do traženog rješenja. Takvi se genetski algoritmi nazivaju hibridnima.

2. Primjena genetskih algoritama

2.1. Izračunavanje optimalnog broja prijava mobilnih telefona baznim stanicama

Lokacijski menadžment je naziv za grupu problema koja se bavi praćenjem korisnika unutar mobilne mreže, koja je predstavljena kao skup geometrijskih ćelija zvanih ćelije. Svaka ćelija ima svoju baznu stanicu koja je zadužena za njeno posluživanje. Bazne stanice su povezane s MSC-om (mobilnim centrom za usmjeravanje) koji služi kao vrata u klasičnu žičanu mrežu. Na slici ispod je prikazana vizualizacija ovdje opisane strukture mreže uz pretpostavku da su ćelije šesterokutnog oblika.

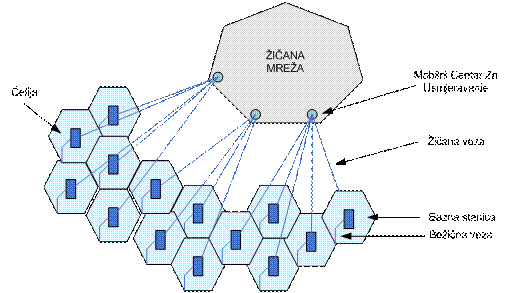
SLIKA 2.1 - Zamišljena arhitektura mobilne mreže

Većina komercijalnih mreža je podjeljeno u lokacijska područja (LA), koja se mogu sastojati i od više ćelija, a od korisnika se zahtjeva da se prijavi pri ulasku u lokacijsko područje. Ta prijava ima određeni trošak zbog zauzimanja resursa kao i zbog potroška energije. Cilj je taj trošak minimizirati, odnosno pronaći optimalan plan prijave za svakog pojedinog korisnika koji će reći da li da se taj korisnik prijavi u određenom lokacijskom području ili ne. Kako bi se taj problem riješio potrebno je poznavati koliko često i kojom brzinom korisnik mijenja lokacijska područja te koliko često prima pozive. Ako korisnik često mijenja lokacijska područja, ima malu vjerojatnost dolaska poziva i veliku cijenu prijave tada je logično da će preskakanje prijave u nekoliko lokacijskih područja dovesti do minimizacije sveukupnog troška svih prijava.

Prije samog opisa rješenja pomoću genetskog algoritma bitno je spomenuti da su ovaj problem pokušavale riješiti i druge heurističke metode koje imaju ugrađena velika ograničenja koja ih sprečavaju pri izračunu minimalnog troška. Neka od tih ograničenja su ignoriranje kretanja korisnika, ignoriranje vjerojatnosti dolaska poziva te ograničenost u obliku ćelija zbog jednostavnije analize, iako u stvarnosti ćelije mogu biti bilo kojeg oblika. Kao što se vidi ova ograničenja su velik problem zbog toga što su baš ona varijable problema.

Genetski algoritam koji rješava opisani problem koristi binarni prikaz kromosoma, koji se interpretira na slijedeći način: ako je na nekom mjestu unutar binarnog stringa jedinica, tada se u toj lokacijskoj jedinici radi prijava, a ako je na tom mjestu nula tada se prijava ne radi. Iz ovoga se može zaključiti da je duljina stringa jednaka broju lokacijskih područja. Početna populacija se bira slučajnim odabirom, no kako bi algoritam brže konvergirao ka optimumu može se poslužiti statističkim podacima o vjerojatnosti dolaska poziva kako bi početna populacija imala veći broj nula(za manju vjerojatnost) ili veći broj jedinica (za veću vjerojatnost) u svakom pojedinom kromosomu. Funkcija dobrote dana je kao recipročna vrijednost cijene prijave za pojedini kromosom. To pak znači slijedeće: što je cijena manja, dobrota kromosoma je veća. Funkcija selekcije temeljena je na roullete-wheel selekciji što omogućuje da bolji kromosomi imaju i više od jedne kopije u slijedećoj generaciji. Nakon selekcije dolazi do križanja i mutacije kako bi se dodatno izmjenili kromosomi za slijedeću generaciju. Parametar za križanje korišten u algoritmu je 0.8, a za mutaciju je 0.01. Na kraju se izračunaju dobrote novih kromosoma i cijeli se ciklus ponavlja.

Jedan primjer rezultata rada algoritma prikazuje slijedeća tablica u kojoj je λ vjerojatnost dolaska poziva, C_ucijena pojednične prijave, a C_p cijena „paginga“ što je naziv za konstanto traženje korisnika unutar cijele mreže. Do optimalnog se rješenja došlo unutar 1000 generacija. Iz tablice je također vidljivo da za malu vjerojatnost dolaska poziva i za visoku cijenu prijave broj nula u kromosomu dominira.

C_u/C_p	Optimalna Strategija
C_u/C_p	λ = 0.25	λ = 0.5	λ = 0.75
.1	1111111111	1111111111	1111111111
.2	1111111111	1111111111	1111101111
.3	1111001111	1111101111	1111101111
.4	0110010110	1111001111	1111001111
.5	0001001000	1111001111	1111001111
.6	0001001000	1110100111	1111000111
.7	0000100000	1110000111	1110001111
.8	0000100000	0110000110	1110000111
.9	0000010000	0110000110	1110000111
1	0000010000	0110000110	1110000111

TABLICA 2.1 - Optimalne strategije za različite parametre

Algoritam je jednostavan za implementaciju, za rad zahtjeva dva statistička parametra do kojih je lako doći i nema nikakvih ograničenja klasičnih metoda koja bi ga odvukla od optimuma.

Originalni naslov:

„A New Location Update Strategy for Cellular Networks and its Implementation using a Genetic Algorithm“

Autori:

Sajal K. Das, Sanyoj K. Sen

Dostupan na:

ACM, http://www.acm.org

2.2. Dizajn topologije lokalnih mreža

Dizajn topologije LAN-a je složen kombinatorički problem koji se klasificira kao NP – težak problem. Kako ne postoje polinomijalni algoritmi koji bi rješavali ovaj problem, za njegovo se rješavanje koriste heuristički algoritmi. Cilj algoritma je napraviti raspored s minimalnim prosječnim kašnjenjem u mreži. Problem se može podijeliti na dva glavna dijela:

1a) u koliko segmenata treba podijeliti mrežu

1b) kako dodjeliti korisnike svakom segmentu tako da jedan korisnik pripada samo jednom segmentu

2) problem usmjeravanja koji je definiran kao određivanje veza između segmenata u razapinjuće stablo

Kako bi se rješenje lakše razumijelo, uz kratak opis problema slijedi i opis promatranog modela. Neka se LAN sastoji od N korisnika. Matrica prometa između korisnika je matrica tipa n x n koja opisuje zahtjeve između pojedinih korisnika. Jedan element te matrice predstavlja promet između dva korisnika, a bitna karakteristika tog prometa je da on može biti jakog, slabog ili nikakvog intenziteta te da može biti privremen ili konstantan. Za potrebe ovog algoritma pretpostavlja se da su prometne karakteristike poznate.

Također sam je LAN podijeljen u P segmenata (token-ring, ethernet,...) koji su povezani mostovima (bridgevima). Svaki segment je poznatog kapaciteta, ali svaki je segment drugačiji po ponašanju od ostalih segmenata. Kašnjenja unutar pojedinih segmenata utječu na kašnjenje cijele mreže, a kako promet unutar jednog segmenta teži njegovom kapacitetu, tako i prosječno kašnjenje unutar tog segmenta teži ∞. Kašnjenju još dodatno pridonosi i kašnjenje mostova zbog pretraživanja unutar look-up tablica i čekanja paketa u redu za ulaz u slijedeći(odredišni) segment. Prije samog opisa genetskog algoritma još jedna potvrda kompleksnosti problema je i veličina prostora rješenja koja je definirana formulom (1) (P i N su definirani u prethodnim odlomcima)

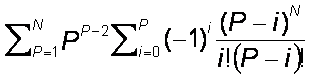(1)

Segmenti LAN-a se spajaju u oblik razapinjućeg stabla. Kako se LAN sastoji od P segmenata tako i stablo ima P čvorova. Svaki čvor ima maksimalno P-1 dijete, a maksimalna dubina stabla je P div 2. Ovakav raspored zahtjeva i odgovarajuću strukturu podataka, a genetski operatori moraju biti takvi da primjenjeni na jedno stablo kao rezultat daju novo razapinjuće stablo.

Stoga je za tip podataka odabrano razapinjuće stablo prikazano kao rijetko Huffmanovo stablo. Svaki čvor u tom stablu ima jedinstvenu oznaku koja ujedno predstavlja i put od korijena do tog čvora gdje je duljina oznake jednaka duljini puta.

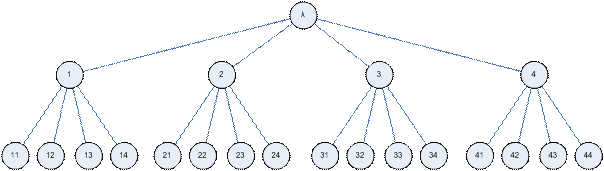
SLIKA 2.2 - Virtualno Huffmanovo stablo s P = 5

Na slici je predstavljeno virtualno Huffmanovo stablo s P = 5. λ označava korjen stabla, a grane su označene s 1,2,3,4. List (put) s oznakom 32 označava da se treba spustiti u granu 3 i ići do drugog (2) lista u toj grani.

Kako bi se ovakav način označavanja mogao uspješno koristiti za prikaz kromosoma potrebno je da sve oznake čvorova budu jednake duljine. U tu se svrhu kodiranju dodaju „0“ na kraj sve dok se na dođe do pune duljine oznake. Na ovaj se način može prikazati bilo koja LAN topologija.

Početna se populacija stvara tako da se generira P slučajnih Huffmanovih oznaka. Kako one na moraju biti inicijalno vezane u valjano stablo radi se postupak fiksacije prikazan na slijedećoj slici.

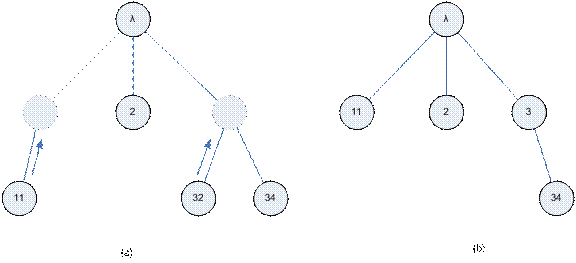
SLIKA 2.3 - Fiksiranje virtualnog Huffmanovog stabla. (a) odabrani čvorovi i (b) fiksirano stablo

Detaljnije pojašnjenje samog postupka fiksacije nalazi se u izvornom članku. Za prikazani slučaj kromosom izgleda ovako: 0010203034.

Nakon fiksacije definiran je broj segmenata u koji će biti podjeljena mreža kao i veze između LAN-ova. Još treba odrediti prikaze ostalih dijelova problema. Oni se definiraju kao dva dodatna kromosoma. Drugi kromosom sadrži redoslijed dodjeljivanja segmenata.Treći kromosom predstavlja distribuciju korisnika unutar jednog segmenta. Rješenje je pojednostavljeno prikazano kao {C_conf,C_clust,C_order}. Genetski operatori se primjenjuju na sva tri kromosoma. Funkcija dobrote je predstavljena kao recipročna vrijednost prosječnog kašnjenja čime je postignuta veća vrijednost dobrote za manje kašnjenje. Primjeri rada algoritma kao i dodatne formule koje pojašnjavaju problem nalaze se u originalnom članku.

Originalni naslov:

„Topological Design of Local-area Networks Using Genetic Algorithms“

Autori:

Reuven Elbaum, Moshe Sidi

Dostupan na:

http://www-comnet.technion.ac.il/moshe/PUBS/m_sidi_topology_96.pdf

2.3. Raspoređivanje instrukcija

Raspoređivač instrukcija kao pojam označava odabir, iz velikog skupa konkurentnih instrukcija, jednog kombinaciju koja smanjuje i vrijeme izvođenja i prostor koje program, čije su to instrukcije, zauzima. S obzirom na to da je ovo jako kompleksan problem klasične metode pretraživanja ne daju dobre rezultate, a kako niti većina heurističkih metoda ne daje dobre rezultate u ovom problemu do izražaja dolaze genetski algoritmi kao dobra metoda pretraživanja prostora rješenja valjanih rasporeda zbog svojih operatora križanja i mutacije. Dodatna pogodnost genetskih algoritama je i to da se oni mogu vremenski ograničiti to jest korisnik može direktno utjecati na duljinu izvođenja algoritma što kod nekih drugih metoda nije slučaj.

Tip podataka korišten za predstavljanje ovog problema je DDD (data dependence dag). Čvorovi u DDD-u su operacije koje se izvode, a lukovi predstavljaju redosljed izvođenja operacija.

Funkcija dobrote za problem je definirana kao broj instrukcija koje sadrže operacije plus duljina puta koji sadrži instrukcije koje se moraju serijski izvoditi. Neki rekombinacijski operatori koji se mogu koristiti za ovaj problem su križanje s dvije točke prekida, rubna rekombinacija, kružno križanje...

Uvijet zaustavljanja algoritma je poseban problem zbog krajnjeg rezultata. Jedan mogući uvjet je približavanje rješenja njegovoj najboljoj teorijskoj vrijednosti. Vremenska ograničenja nisu baš povoljna zbog činjenice da se optimalno rješenje može naći već u prvoj generaciji ili se ne mora naći uopće. Broj generacija kao uvjet je ovisan o složenosti koda koji se optimira. Za složeniji kod potrebno je više generacija kako bi se došlo do optimalnog rješenja.

Originalni naslov:

„Genetic Algorithms and Instruction Scheduling“

Autor:

Steven J. Beaty

Dostupan na:

emess.mscd.edu/~beaty/Dossier/Papers/genetic.pdf

2.4. Jednoliku podjelu hiper - grafova

Kao što sam naslov kaže cilj je podjeliti graf na dva približno jednaka dijela s minimalnim brojem presjeka.Taj se probelm klasificira kao NP – težak.

Genetski algoritam koji rješava ovaj problem ima par specifičnosti i to su: lokalna optimizacija nakon svake iteracije (zato je to hibridni genetski algoritam) te uvođenje grupiranih shema.

Kromosom je predstavljen kao niz bitova onolike duljine koliko ima vrhova u grafu sa slijedećim značenjem: jednica označava da vrh na tom bitovnom mjestu pripada desnom grafu u podjeli, dok nula označava da pripada lijevom grafu. Naziv za ovakvo kodiranje je lokacijsko kodiranje.

Algoritam radi tako da u svakoj generaciji izabere dva roditelja koja se križaju na način prikazan na slici:

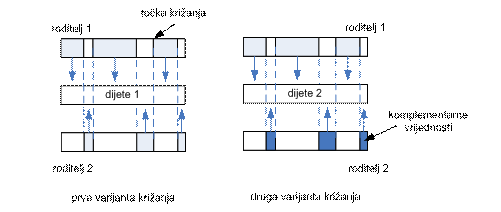
SLIKA 2.4 - Križanje s pet točaka prekida

Kao što se iz slike vidi koriste se dvije varijante križanja s 5 točaka prekida. Razlika u tim načinima križanja je to što se kod desnog križanja na slici koriste komplementarne vrijednosti nekih bitova. To se radi zobg toga jer se može dogoditi slučaj da je jedan roditelj komplement ili skoro komplement drugome što znači da oni zapravo predstavljaju iste ili jako slične grafove (jednaka podjela). Genetski algoritam izabire bolje od dvoje djece te nad tim djetetom provodi mutaciju s vjerojatnošću promjene gena od 0.015.

Nakon mutacije provodi se lokalna optimizacija kao jedan oblik Fidducia – Mattheyses algoritma. To je ujedno i vremenski najzahtjevniji dio algoritma. Nakon lokalne optimizacije algoritam odlučuje da li će dijete ući u populaciju ili ne i to tako da uspoređuje podjelu grafa u djetetu s podjelom u sličnijem roditelju. Ako je podjela djeteta bolja tada ono ulazi u populaciju, inače ne. Kako bi se spriječio velik broj generacija bez promjene populacije genetski algoritam uspoređuje dijete i s drugim roditeljem. Slijedeći pseudokod opisuje rad algoritma

preprocess; /* optional, dodatne pripreme za brži rad algoritma */

create an initial population;

do {

choose parent1 and parent2 from population;

offspring = crossover(parent1, parent2);

mutation(offspring);

local-improvement(o_spring); /* a modiffed FM alg. */

if suited(offspring) then replace(offspring);

} while (stopping criterion not satisfied);

return the best member of the population;

Originalni naslov:

„A Fast and Stable Hybrid Genetic Algorithm for the Ratio-Cut Partitioning Problem on Hypergraphs“

Autori:

Thang Nguyen Bui, Byung Ro Moon

Dostupan na:

ACM, http://www.acm.org

2.5. Djeljenje grafova i inkrementalno djeljenje grafova

Problem podjele grafa na jednako velike grupe čvorova, s minimalnim brojem lukova između različitih grupa, je jako važan problem u paralelnom računarstvu. Npr. u višeprocesorskom sustavu poželjno je da se aplikacije izvode što je moguće više paralelno, da se podaci jednoliko raspodjele na procesore, a sa što manjom međuprocesorskom komunikacijom.

Genetski algoritam koji je ovdje opisan koristi posebno dizajnirane operatore križanja koji značajno unapređuju rad algoritma u odnosu na klasične operatore. Zahvaljujući tome rezultati dobiveni korištenjem ovog genetskog algoritma su bolji ili usporedivi s najboljim metodama za djeljenje grafova s nekoliko stotina čvorova.

Kromosomi su prikazani kao nizovi bitova gdje bitovno mjesto označava čvor, a broj na bitovnom mjestu označava kojoj podjeli taj čvor pripada. Funkcija dobrote definirana je pomoću troška izračuna čvora v_i i troška svih izlaznih vrhova.

Operatori križanja su:

KNUX – neuniformno križanje s znanjem iz prošlosti

DKNUX – dinamički KNUX

KNUX (Knowledge Based Non-Uniform Crossover) operator koristi uniformno križanje, ali sa slijedećim dodatkom: koristi se vektor vjerojatnosti p čije komponente su realni brojevi između 0 i 1 dobiveni iz dobrota roditelja i same specifičnosti problema. Ako su A i B roditelji, C dijete, p vektor vjerojatnosti tada je c_i= a_i ako je a_i = b_i, inače je c_i= a_i s vjerojatnošću p_i.

DKNUX (Dynamic KNUX) tokom rada algoritma konstanto unapređuje vektor vjerojatnosti p_i.

Originalni naslov:

„Genetic Algorithms for Graph Partitioning and Incremental Graph Partitioning“

Autori:

Harpal Maini, Kishan Mehritra, Chilukuri Mohan, Sanjaj Ranka

Dostupan na:

ACM, http://www.acm.org

2.6. Problem pakiranja kutija u tri dimenzije

Klasičan problem pakiranja kutija može se najjednostavnije opisati na slijedeći način: postoji konačan skup paketa koje treba pakirati u skup kutija. Paketi su definirani svojom „težinom“, a kutije kapacitetom.

Ovaj problem ima široku primjenu, od pakiranja kamiona, alokacije memorije u računalima, maksimalnog iskorištenja materijala pri rađenju manjih komada iz velikih ploča,...

Ovaj problem je generalizacija problema dijeljenja i to tako da kutija predstavlja veličinu segmenta, a paketi se moraju optimalno smjestiti u te segmente. Ograničenja u problemu ovise o njegovoj primjeni koja može biti jako široka, što se vidi i iz gore navedenih primjena.

U klasičnom problemu kutija je fiksnog kapaciteta. S proširenjem na više dimenzija analogno se može definirati da svaka dimenzija ima fiksni kapacitet.

3D kutija je podjeljenja na kriške i nivoe. Nivoi su horizontalne granice između dva sloja paketa, a kriške su vertikalne granice između dva sloja.

Mogući načini pakiranja su slijedeći:

3D NextFit – algoritam počinje na prvom nivou i prvoj kriški. Paket se smješta na slijedeću slobodnu poziciju na nivou sve dok se ne dođe do širine kutije. Tada se otvara novi nivo i nastavlja se pakiranje. Baza novog nivoa je najviši paket na nivou. Nova kriška se stvara ako je paket prešao dužinu kutije. Rezultat je visina kutije. Cilj je da bude što manja.

3D FirstFit – početak je jednak kao i u 3D NextFit - u, no kasniji smještaj se radi tako da se pretražuju nivoi sve dok se ne nađe mjesto u koje paket stane. Duljina nivoa se može mijenjati, povećavati tako da paket stane, sve dok se ne dođe do dužine kutije. Nije bitno ako promjena na jednom nivou uzrokuje pomake na drugim novima. Isti princip vrijedi i za kriške.

Kromosom je prikazan kao niz cijelih brojeva: broj 1 predstavlja prvu kutiju, 2 drugu, itd. Funkcija dobrote vraća visinu kutije popunjenu s jednim od ova dva algoritma. Što je visina manja to je pakiranje bolje. Križanje kao rezultat mora dati permutaciju paketa oba roditelja. Za to se koristi PMX, kružno križanje, ... Dijete mora biti takvo da nema duplikata. Mutacija zamjenjuje dva slučajno odabrana paketa i rotira ih oko slučajno odabrane osi. Vjerojatnost mutacije je veća što je veća sličnost roditelja.

Originalni naslov:

„A genetic Algorithm for Packing in Three Dimensions“

Autori:

Arthur L. Corcoran III, Roger L. Wainwright

Dostupan na:

ACM, http://www.acm.org

2.7. Problem ortogonalnog pakiranja

Ovaj problem je jedan podskup problema pakiranja kutija, a problem se može definirati na slijedeći način – neka je dan konačan broj pravokutnika r_i, i = 1, .. ,n i pravokutna ploča zadane širine i beskonačne dužine. Cilj je minimizirati dužinu ploče tako da su svi pravokutnici smješteni na ploči bez preklapanja i tako da su im stranice paralelne sa stranicama ploče.

Algoritam koji rješava dani problem zove se „bottom – left“ algoritam. Jedno pakiranje je označeno kao jedna moguća permutacija pravokutnika

π = (i₁,...,i_n)

i je indeks pravokutnika

Redosljed pakiranja dan je redosljedom indeksa u π. Dodatno poboljšanje algoritma koje se koristi u praksi je slijedeće:

1) prvi pravokutnik se smjesti u donji lijevi kut ploče

2, 3, 4, ...) pomakni i-ti pravokutnik počevši od gornjeg desnog kuta do dna pa onda lijevo koliko god je to moguće, s time da spuštanje ima prioritet

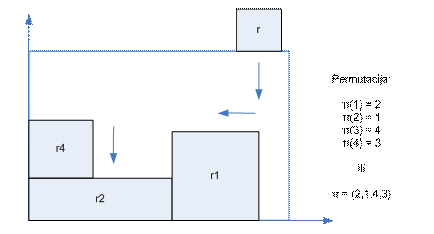
SLIKA 2.5 - Ilustracija BL algoritma

Iz slike se vidi da je prvo r₂ spušten do dna pa gurnut lijevo do kraja. Isto tako i za r₁ i r₄ . Strelica pokazuje način smještaja r₃.

Genetski algoritam je slijedećeg oblika:

SLIKA 2.6 – Skica genetskog algoritma

Početni parametri algoritma su:

početna veličina populacije koja je 100

roullete – wheel slekcija

cikličko križanje

50 % vjerojatnost križanja, 1% vjerojatnost mutacije

kraj nakon 5 generacija

Jedan član populacije je jedna permutacija pravokutnika.

Detaljniji rad algoritma je slijedeći:

1) odredi veličinu danog područja u % svake komponente

2) odredi skup dimenzija za svaku komponentu

On se određuje ili pomoću formula danih u orginalnom članku ili može biti određen prema željama dizajnera na neki drugi način sve dok je zadovoljeno da je dužina x širina uvijek jednaka površini pravokutnika.

3) odredi skup komponenti (permutacije pravokutnika)

U ovom se koraku bira jedna kombinacija za svaki pravokutnik(dužina x širina) koja ulazi u populaciju. Sukladno s time u ovom se koraku bira i početna populacija slučajnim odabirom premutacija.

4) izračunaj dobrotu svakog člana populacije

f(x) = H(x) – IzgubljenoPodručje / (h * w)

gdje je

H(x) = (H-h) / H

H je velika konstanta da se osigura pozitivan H(x)

IzgubljenoPodručje = Ukupno – PovršinaSvihPravokutnika

h = visina uzorka

w = širina uzorka

Cilj je minimizirati visinu ploče, no ovako definirana funkcija dobrote, kaže da što joj je veća vrijednost to je jednika bolja!

5) provjeri da li je zadan kriterij optimalnosti zadan od dizajnera. Ako je, sačuvaj najbolja rješenja i ponovi postupak za drugu kombinaciju komponenti. Ako nisu zadovoljeni uvjeti radi se roullete - wheel selekcija, jednostavno križanje između roditelja te mutacija koja mijenja slučajne članove unutar jedne permutacije. Veličina nove populacije je dva puta veličina stare populacije. Sada se opet provodi BL algoritam i ponavlja se postupak pod 4 i 5 sve dok ne bude zadovoljen kriterij optimalnosti.

Originalni naslov:

„AN EXTENSION OF THE ORTHOGONAL PACKING PROBLEM THROUGH DIMENSIONAL FLEXIBILITY“

Autori:

Alison R. Callaghan, Anoop R. Nair, Kemper E. Lewis

Dostupan na:

does.eng.buffalo.edu/publications/ publications/DETC99_DAC-8588.pdf

2.8. Numeričku optimizaciju funkcija

GAVIn (Genetic Algorithms Visual Interface) je MS Windows aplikacija koja opisuje osnovne principe rada genetskih algoritama kroz numeričku optimizaciju funkcija. Aplikacija omogućuje korisniku da mijenja parametre genetskog algoritma kako bi korisnik sam mogao vidjeti kako različite postavke parametara utječu na rad algoritma. Program koristi binarni prikaz kromosoma jer je on standard za ovaj tip problema.

Korisnik može sam definirati duljinu kromosoma, veličinu populacije, način završetka rada algoritma, vrstu selekcije, vrstu križanja, vrstu mutacije i još dosta drugih parametara. Uz to program ima ugrađene testne funkcije kojima se može provjeravati rad programa.

Originalni naslov:

„A Genetic Algorithms Tutorial Tool for Numerical Function Optimisation“

Autori:

E.K.Burke, D.B. Varley

Dostupan na:

ACM, http://www.acm.org

2.9. „Učenje kretanja“ 3D likova u simuliranom svijetu

Moderna računalna animacija zahtjeva sve više i više od svojih likova kako bi oni izgledali što realnije u svojim pokretima. Ovaj rad opisuje jedan jednostavan svijet s trenjem, gravitacijom i bićem koje živi u tom svijetu. Želja je iskoristiti genetski algoritam kako bi to biće naučilo kretati se i skakati ne bi li došlo do cilja. Biće je predstavljeno pomoću kocaka koje su spojene oprugama. Neke opruge su fiksne dok su druge fleksibilne (predstavljaju mišiće). Svijet je tako modeliran da u njemu vrijede zakoni fizike.

Kromosomi u genetskom algoritmu su definirani kao kretnje pojedinog mišića (kromosom sadržava informaciju o trenutom položaju svih mišića). Akcija koju mišić može imati je širenje, stezanje ili mirovanje.

Algoritam radi na slijedeći način:

1) izračunaj dobrotu svake jedinke

2) kopiraj najboljih deset jedinki u novu populaciju koristeći roulette - wheel selekciju

3) slučajno odaberi dva roditelja i križaj ih

4) predodređenom broju jedinki zamijeni jedan gen

5) kopiraj najbolju jedinku u novu generaciju kako bi se spriječila degeneracija

Iz ovoga se vidi da su genetski algoritmi jako korisni u kreiranju kompleksnih pokreta uz ispravno definiranu funkciju dobrote. No u dinamičkim situacijama(poput igara) rezultati baš i nisu tako dobri ako se ne koriste trikovi pri stvaranju slike.

Originalni naslov:

„Goal oriented control of simulated physical systems with genetic algorithms“

Autor:

Teemu Maki - Patola

Dostupan na:

http://www.tml.hut.fi/~tmakipat/GA.pdf

2.10. Sintezu sklopovlja i programa

MOGAC je program koji služi za sintezu distribuiranih heterogenih hardver – softver sustava koristeći višeciljne genetske algoritme. Algoritam koristi niz ograničenja kako bi sveo na optimum i cijenu i potrošnju energije budućeg sustava. MOGAC je sposoban generirati sustav s više procesnih elmenata s višestrukim sabirnicama i vezama točka – do – točke.

Problem sinteze ove vrste spada u probleme višeciljne optimizacije zato jer postoji puno vrsta troškova koje treba uzeti u obzir, a među njima postoji takva ovisnost da se smanjenjem jednog troška najčešće povećava neki drugi trošak. Višeciljni genetski algoritmi rješavaju ovaj problem tako da rješenja relativno poredaju prema drugim rješenjima (redni broj rješenja je broj drugih rješenja kojima je to rješenje superiorno) za razliku od drugih metoda koje taj problem znaju rješavati tako da samo spoje troškove u jednu vrijednost.

Najvažniji operator kojeg MOGAC posjeduje je operator križanja jer taj operator daje svu snagu ovog algoritma zbog toga što omogućuje da različita rješenja međusobno dijele informacije. Uz to parametri algoritma su samo prilagodljivi, što znači da ukoliko u jednoj generaciji ne dođe do poboljšanja vjerojatnost mutacije i kromosoma se povećava. Kad se pak dogodi poboljšanje vrijednosti se vraćaju na inicijalne vrijednosti. Algoritam staje ako prođe određen broj generacija bez ikakvog poboljšanja.

MOGAC posjeduje svojstvo elitizma koje je korisnički prilagodljivo, korisnik može sam odlučiti da li će se najbolje jednike sačuvati ili se mogu mijenjati koristeći križanje i mutaciju. Dodatna posebnost MOGAC-a je i to da se operatori dijele na operatore koji djeluju na nivou cijelog rješenja i na operatore koji djeluju na nivou pojedinih skupina unutar pojedinog rješenja.

Ovo je samo kratak opis problema kao i prikaz najvažnijih dijelova MOGAC-a, sve je to detaljno obrađeno u originalnom članku, uz primjer rada samog programa(usporedbe u radu s drugim programima tog tipa).

Originalni naslov:

„MOGAC: A Multiobjective Genetic Algorithm for the Co-Synthesis of Hardware-Software Embedded Systems“

Autori:

Robert P. Dick, Niraj K. Jha

Dostupan na:

ACM, http://www.acm.org

2.11. Rješavanje problema n – kraljica

Problem n – kraljica je jedan od onih problema koji je jako jednostavan za definiciju, ali je jako kompliciran za implementaciju. Definicija problema je slijedeća: kraljica je šahovska figura (može se kretati u svim smjerovima, dok se god kreće u pravocrtnoj liniji), cilj je rasporediti n kraljica na ploču veličine n x n tako da se niti jedna kraljica ne tuče međusobno, to jest da niti jedna kraljica iz svog položaja ne može napasti bilo koju drugu kraljicu.

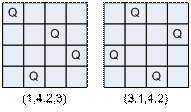
SLIKA 2.7 – Prikaz kromosoma pomoću četvorki

Broj svih mogućih kombinacija je n² povrh n, što ovaj problem čini jako teškim, no dobra stvar je što se već u startu može eliminirati velik broj kombinacija pametnim prikazom jedne kombinacije. Na slici 1 je jedan prikaz koji omogućuja eliminaciju jednog dijela rješenja, a koje se koristi i za ovaj algoritam. Jedna kombinacija je prikazana kao n – torka svih kraljica tako da svaki član n – torke govori u kojem se redu nalazi neka kraljica, dok njegova pozicija unutar n – torke govori u kojem stupcu je ta kraljica. Na ovaj način su rješene sve moguće konfliktne situacije u kojima se mogu naći dvije kraljice ako se nalaze u istom redu ili stupcu. To je moguće zbog vrlo važnog ograničenja koje kaže da su brojevi u n – torci svi međusobno različiti. Time složenost naglo pada na n! no kako je to još uvijek jako velika složenost u igru ulaze genetski algoritmi.

Jedan kromosom u genetskom algoritmu je jednak jednoj n – torci definiranoj na gore opisan način. Operator križanja je definiran kao križanje s dvije točke prekida, ali postoji problem koji se vidi na slici 2.8. Problem je što pri križanju može doći do duplikata unutar jedne n – torke,

(2 5 1 | 3 8 4 | 7 6)

(8 4 7 | 2 6 1 | 3 5)

postaje

(2 5 1 | 2 6 1 | 7 6)

(8 4 7 | 3 8 4 | 3 5)

SLIKA 2.8 – Križanje s dvije točke prekida s neispravnim n – torkama

Taj se problem rješava na slijedeći način:

(2 5 1 | 3 8 4 | 7 6) (2 5 1 | 3 8 4 | 7 6)

(8 4 7 | 2 6 1 | 3 5) (8 4 7 | 2 6 1 | 3 5)

postaje postaje

(2 5 1 | 2 6 1 | 7 6) (3 5 4 | 2 6 1 | 7 8)

(8 4 7 | 3 8 4 | 3 5) (6 1 7 | 3 8 4 | 2 5)

SLIKA 2.9 – Na lijevoj strani slike nalazi se križanje sa slike 2.8, dok se na desnoj strani nalazi ispravno križanje korištenjem PMX - a

Za prvo dijete – dvojka na poziciji 1 je u sukobu s dvojkom na poziciji 4. Kako je dvojka na poziciji 4 novija dvojka na poziciji 1 se mijenja u vrijednost koja je bila na poziciji 4 prije križanja to jest u vrijednost 3. Ovakvo križanje se zove Partially Matched Crossover (PMX). Operator mutacije je s druge strane skroz jednostavan i on samo zamijenjuje mjesta dva broja unutar jedne n – torke čime je ujedno i sačuvana raznolikost svih članova n – torke.

(3 5 4 2 6 1 7 8)

postaje

(3 1 4 2 6 5 7 8)

SLIKA 2.10 – Jednostavna mutacija

PMX način križanja ima problem da želi unificirati populaciju smanjujući time brzinu pronalaženja optimuma pa je preporučljivo u kasnijoj fazi rada algoritma za operator križanja koristiti onaj defniran za mutaciju.

Osim ovog problema postoji i problem pri određivanju funkcije dobrote, a taj problem je slijedeći: genetski algoritmi vole dobrote koje imaju puno vrijednosti kako bi se vidjela raznolikost populacije, a u ovom slučaju rješenje ima samo dvije vrijednosti ili je ispravno ili nije. Stoga se time doskočilo uvođenjem funkcije zadovoljivosti koja ima rješenja u intervalu [0,1] to jest ispravna rješenja imaju vrijednost 1, a ona neispravna se rangiraju po tome da li više neispravna (bliže nuli) ili više ispravna (bliže jednici). Uz ovakvu defniciju dobrote može se koristiti i ona jednostavnija, a to je da se samo pobroje konflikti među kraljicama. Rješenja kao i vremena izvođenja su usporediva za obje definicije funkcije dobrote.

Originalni naslov:

„Solving the n – Queens Problem Using Genetic Algorithms“

Autor:

Kelly D. Crawford

Dostupan na:

ACM, http://www.acm.org

2.12.Učenje Bayes – ianskih kasifikacijskih pravila

DELVAUX je sustav za induktivno učenje koji koristi genetske algortime za proces učenja. Sustav služi za učenje Bayes – ianskih klasifikacijskih pravila iz skupa primjera. Ukratko Bayesianska klasifikacijska pravila su mješavina simboličkih i numeričkih vrijednosti. Simboličke vrijednosti su uvjeti s lijeve i desne strane, a numeričke su npr. vrijednost koja predstavlja težinu nekog svojstva u nekom skupu pomoću kojeg će sustav reći da li je za ili protiv nekog zaključka. Jedan primjer takvog pravila je slijedeći:

If E then (to degree S,N) H

gdje su S i N veličine pomoću kojih se određuje zadovoljivost i potrebitost H za E.

Jedan kromosom je skup pravila sa svojstvom da različiti kromosomi mogu biti različith duljina. Operator križanja je križanje s jednom točkom prekida sa svojstvom da roditelji tokom križanja međusobno izmjenjuju pravila. Do nejednakosti u duljini kromosoma dolazi kada točka prekida nije postavljena na ista mjesta u oba roditelja.

roditelj 1: r₁ | r₂ r₃ 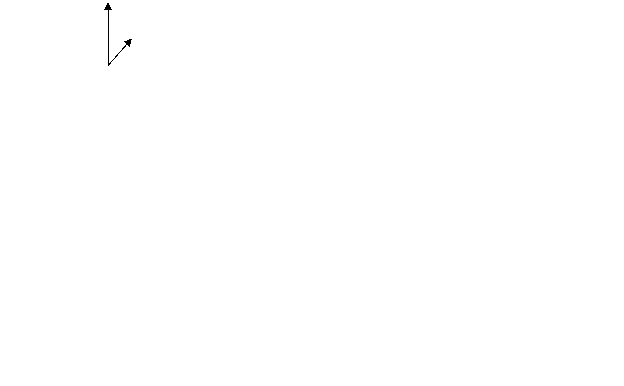r₄ dijete 1: r₁ s₄

roditelj 2: s₁ s₂ s₃ | s₄ dijete 2: r₂ r₃ r₄s₁ s₂ s₃

točke prekida

Optimalnu kardinalnost algoritam sam uči. Operator mutacije radi tako da jedno pravilo izbaci van iz skupa pravila i na njegovo mjesto stavi slučajno izgrađeno pravilo. Uz ova dva operatora koristi se i operator inverzije koji radi tako da promjeni mjesta pravila unutar kromosoma što utječe na kompozicije budućih generacija (zbog križanja). Broj članova populacije je konstantan kroz sve generacije. Najbolji član populacije uvijek preživljava.

slijedeca_generacija(t) : =

UMETNI najbolji_clan_od (G (t)) u G(t+l) ;

DO {

Odaberi clanove rul i ru2 iz G(t) slucajnim odabirom;

Cini {

Ako treba_krizati

tada krizaj(rul, ru2, rul’, ru2’)

inace { rul' :=rul; ru2':= ru2 }

Ako treba_mutirati tada rul’:= mutiraj(rul’);

Ako treba_mutirati tada ru2’:= mutiraj(rul’);

Ako treba_invertirati tada rul’:= invertiraj(rul’);

Ako treba_invertirati tada ru2’:= invertiraj(ru2’);

Umetni rul’ u G(t+l);

Umetni ru2’ u G(t+l) }

S VJEROJATNOSCU h’(rul)*h’(ru2); }

DOK NIJE populacija G(t+l) popunjena;

SLIKA 2.11 – Generiranje slijedeće generacije

Ova slika predstavlja način nastajanja nove generacije (ru1, ru2 su roditelji; ru1' i ru2' su djeca). Ako treba ... predstavlja vjerojatnost obavljanja te operacije.

Također bitno je i reći da se cijeli taj kod obavlja s određenom vjerojatnošću koja je određena kao h'(ru1) * h'(ru2) gdje je h'

(2)

gdje su:

r je broj pravila u skupu pravila,

p je broj premisa,

c je broj konkluzija,

h(ru) je dobrota pojedinog pravila određena kao postotak dobro klasificiranih slučajeva.

Originalni naslov:

„Learning Bayesian Classification Rules through Genetic Algorithms“

Autori:

Christoph F. Eick, Daw Jong

Dostupan na:

ACM, http://www.acm.org

2.13. Proračun smještaja makro ćelija

Jedna moguća definicija problema je:

Za slijedeće ulazne vrijendosti:

1) postoji skup pravokutnih ćelija, s izvodima na rubovima

2) mrežna lista koja opisuje spajanje izvoda

3) horizontalana duljina pločice W

algoritam treba pronaći

1) apsolutne koordinate donjeg lijevog kuta svake ćelije

2) točan položaj svake ćelije (orijentacija i rotacija)

3) pravokutnik širine W minimalne duljine takav da su sve ćelije smještene na

njemu

uz ova ograničenja

1) ćelije se ne smiju preklapati

2) pravokutnik mora ostaviti dovoljno mjesta između ćelija da se sve

međusobne veze mogu ostvariti

Problem je zapravo sličan problemu 2D pakiranja kutija što će se kasnije i vidjeti jer program koristi BL – algoritam za smještaj ćelija na ploćicu. Složenost ovako definiranog problema je O(n! 8ⁿ) što ga čini jako teškim problemom za rješavanje.

Rad algoritma prikazan je na slici 2.12:

generiraj(P_C);

evaluiraj(P_C);

ponavljaj noOfGenerations puta:

P_N := 0;

ponavljaj noOfOffspring puta:

odaberi p₁ € P_C, p₂ € P_C;

P_N := P_N U krizaj(p₁, p₂);

kraj;

evaluiraj(P_C U P_N);

P_C := odaberi(P_C U P_N);

zaSvaki p € P_C : moguca_mutacija (p);

evaluiraj(P_C);

kraj;

q := oadberi Najboljeg;

optimiziraj(q);

SLIKA 2.12 – Skica Algoritma

Kromosom je prikazan kao stablo u kojem svaki čvor predstavlja jednu ćeliju, a lukovi su orijentirani i dijele se na „top - edges“ i „right - edges“. Za jedan čvor top – edge pokazuje na čvor koji je fizički iznad njega, a right – edge je čvor koji je fizički desno do njega (čvor = ćelija). Iz ovoga je očito da svaki čvor ima maksimalno jedan top i jedan right edge. Korijen stabla je ćelija koja se nalazi u donjem lijevom kutu.

Funkcija dobrote u sebe uključuje površinu koju zauzimaju ćelije i što manju duljinu žica koje spajaju ćelije.

Operator križanja između dva roditelja daje dijete tako da izabere povezani skup čvorova iz jednog roditelja i prema zadanim pravilim doda ostale čvoroe iz drugog roditelja.

Postoji pet vrsta mutacija koje su definirane za ovaj problem, sve se odvijaju nad ćelijama. Jednostavnije su rotacija ćelije, promjena orijentacije ćelije, promjene susjeda jedne ćelije....

Naravno pri mutacijama se mora uvijek provjeravati da li su zadovoljena ograničenja.

Originalni naslov:

„A Genetic Algorithm for Macro Cell Placement“

Autor:

Henrik Esbensen

Dostupan na:

http://www.ee.utulsa.edu/~tmanikas/Pubs/Manikas-MWSCAS-02-final.pdf

2.14. Sintezu CMOS operacijskih pojačala

Pri izradi elektroničkih sustava puno više vremena odlazi na izradu analognih dijelova nego digitalnih. Razlog tome je to što postojeće analogne komponente najčešće nisu dovoljne za izradu svih potrebnih funkcija pa se stoga ostatak mora raditi ili ručno ili pomoću alata za sintezu. Ovdje je predstavljen jedan takav alat - DARWIN.

Svojstva DARWIN-a su slijedeća:

- simultan odabir topologije i „circuit sizing“

- program sam gradi topologiju koristeći dostupne elemente

- za odabir topologije i „circuit sizing –a“ koristi se genetski algoritam

- za program nije potrebno veliko dizajnersko znanje

- na početku sinteze za svaku građevnu jedinicu provjeravaju se ograničenja kako bi se osiguralo da tokom izgradnje uvijek postoji željeno ponašanje sklopa

Svako operacijsko pojačalo sastoji se od tri dijela: ulaznog dijela, opcionalnog

pojačavačkog dijela i izlaznog spremnika.

Na temelju toga može se konstruirati velik broj različitih topologija. No ipak, samo neke od tih topologija mogu raditi kao operacijsko pojačalo. Na slici je prikazana spojna matrica koja pokazuje koji su elementi međusobno kompatibilni. Križić na mijestu (i,j) označava da element j može doći iza elementa i.

	2	3	4	5	6	7	8	9	10	11	12	13
1	X	X	X	X									1	input
2						X			X			X	2	nMOS diff. Pair(simple)
3					X					X		X	3	pMOS diff. Pair(simple)
4							X			X		X	4	nMOS folded cascode
5								X	X			X	5	pMOS folded cascode
6									X	X	X	X	6	nMOS CS
7									X	X	X	X	7	pMOS CS
8									X	X	X	X	8	nMOS CS with level shift
9									X	X	X	X	9	pMOS CS with level shift
10												X	10	nMOs source follower
11												X	11	pMOS source follower
12												X	12	class AB output buffer
													13	output

SLIKA 2.13 – Spojna matrica

Uz ovo ograničenje postoje još i dodatna ograničenja koja pobliže određuju željeno ponašanje pojačala.

U DARWIN-u su građevni elementi prikazani pomoću svojeg imena i k – dimenzionalnog vektora α čiji su elementi iz skupa {0,1}. Taj vektor sadrži opise svih traženih ograničenja za pojedini element.

Početna populacija sadrži neka moguća rješenja, dakle rješenja koja nisu optimalna, ali zadovoljavaju sva zadana ograničenja. Slijedeći korak, nakon generiranja početne populacije, je izračunavanje dobrote jedniki koja je definirana na temelju disipacije energije. Prije ulaska u sam genetski algoritam sve se dobrote skaliraju na vrijednosti između 0 i 1 tako da najslabija jednika ima vrijednost jedan a najlošija nula. Sada dolazi do stvaranja novih jedniki pomoću križanja i mutacije, a broj novih jedniki jednak je broj_populacije * vjerojatnost križanja. Operator križanja radi na slijedeći način: prvi blok (ulazni stupanj) roditelja A se kopira u novu topologiju, drugi blok se uzima od roditelja B ako je to moguće. Na kraju se blok tri uzima od roditelja koji nije dao blok dva, ako je to moguće s obzirom na spojnu matricu. Dodatno je uz ovakvo križanje moguće da se i α vektori roditelja križaju (križanje s dvije točke prekida). Mutacija je izvedena tako da mijenja mali broj elemenata unutar α vektora.

Originalni naslov:

„DARWIN: CMOS opamp Sythesis by means of a Genetic Algorithm“

Autori:

Wim Kruiskamp, Domine Leenaerts

Dostupan na:

ACM, http://www.acm.org

2.15.Modeliranje, dizajn i kontrolu procesa

Ovdje su opisane tri primjene genetskih algoritama u rudarskoj industriji.

Prva je za modeliranje „Ree - Eyring“ jednadžbe koja opisuje proces odstranjivanja vode iz minerala. Genetski algoritam se koristi za određivanje optimalnih konstanti za jednadžbu kako bi se što preciznije mogao riješiti zadani problem.

Druga primjena je dizajn zrakom upuhivanog hidrociklona. To je uređaj koji služi za razdvajanje minerala. Cilj je odrediti optimalne vrijednosti svih parametara kako bi se dobile maksimalne performanse.

Treća primjena je vezana uz fuzzy logičke kontrolore. Genetski algoritam se koristi kako bi se odabrale ili dodatno optimizirale funkcije fuzzy logičkog kontrolora. Te funkcije daju značenja lingvističkih izraza fuzzy kontorlora. Konkretna primjena je kontrola laboratorijskih pH sustava.

Ove primjene genetskih algoritama su dovele do značajnih smanjenja troškova kako u izradi tako i u korištenju izrađenih objekata.

Originalni naslov:

„GENETIC ALGORITHMS FOR MODELLING, DESIGN, AND PROCESS CONTROL“

Autor:

Charles L. Karr

Dostupan na:

ACM, http://www.acm.org

2.16. Rješavanje „Busy – Beaver“ problema

„Busy Beaver“ je teorijski problem koji se definira na slijedeći način:

Pretpostavka je da postoji Turingov stroj s beskonačnom trakom na obje strane i s znakovima trake iz skupa {blank, 1}. Pitanje je koliki je maksimalni broj jedniica koji se može zapisati pomoću zaustavljivog Turingovog stroja s N stanja ( stanje u kojem stroj staje nije uključeno u ovh N) kada počne pisati na praznu traku?

Oznaka za taj broj je Σ (N) gdje je N broj stanja. Stroj koji to radi zove se Busy Beaver (BB). Funkcija Σ (N) nije izračunljiva. Već za N = 5 se ne može sa sigurnošću odrediti taj broj. Iako je problem originalno zamišljen za Turingove strojeve koji barataju s 5 – orkama rješenje koje je ovdje prezentirano radi s 4 – orkama. Turingov stroj s 5 – orkama radi tako da pomoću stanja u kojem je i znaka na traci odlučuje koji će simbol zapisati na traku, u koje će stanje otići i kamo će se pomaknuti (lijevo, desno ili će ostati na toj ćeliji). Turingov stroj koji radi s 4 – orkama radi tako da ili zapisuje novi znak na traku ili se pomiče lijevo ili desno (ne može napraviti obje operacije istovremeno).

Rješenje ovdje prezentirano radi za BB(7). Stroj ima 7 stanja i najbolji razultat koji je postignut je Σ (N) ≥ 102.

Za Turingov stroj s 4 – orkama produktivnost se definira kao duljina niza jednica napravljenih počevši na praznoj traci i s zaustavljanjem na najlijevijoj jednici, s ostatkom trake praznom. Svi Turingovi strojevi koji se ne zaustavljaju na taj način ili se ne zaustavljaju uopće imaju produktivnost 0.

Svaka jednika je jedno rješenje, a svaka jedinka je zakodirana u formatu prikazanom na slicu kao binarni string.

SLIKA 2.14 – Kodiranje jedinki

Svaki blok se sastoji od po 5 bitova(tri bita za stanje i dva bita za akciju). S ovakvom definicijom jedinki (kromosoma) mogu se slobodno koristiti operatori križanja i mutacije bez straha da će se izaći van prostora rješenja.

Pri izračunu funkcije dobrote korišteni su slijedeći faktori poredani po važnosti:

1) zaustavljanje prije predodređenog broja koraka

2) ponašanje u skladu s pravilima

3) produktivnost

4) broj korištenih prijelaza

5) broj koraka prije zaustavljanja

Neke jednike unutar populacije imaju još dodatno ugrađenu sposobnost učenja, to jest pomoću hill – climbing metode (Lamarckian learning) traže lokalni optimum u svojoj okolini kako bi poboljšale svoju funkciju dobrote. Na slici se nalazi najbolje dobiveni Turingov stroj prikazan kao konačni automat i kao tablica prijelaza.

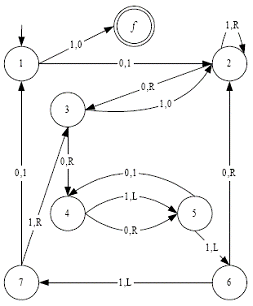
δ	Za Blank		Za Jedinicu
Stanje	Novo Stanje	Akcija	Novo Stanje	Akcija
1	2	1	f	L
2	3	R	2	R
3	4	R	2	0
4	5	r	5	L
5	4	1	6	L
6	2	R	7	L
7	1	1	3	R

SLIKA 2.15 – Turingov stroj i njegova tablica prijelaza

Ako se želi napasti veći N pomoću ovog algoritma potrebno je napraviti određene promjene kako bi algoritam brže radio.

Originalni naslov:

„Busy Beaver – An Evolutionary Approach“

Autori:

Francisco B. Pereira, Penousal Machado, Ernesto Costa, Amilcar Cardoso

Dostupan na:

http://eden.dei.uc.pt/~amilcar/publ/bbeaver.pdf

2.17.Dizajn prospojne mreže u digitalnim sklopovima

Dizajn prospojne mreže je završna faza fizičkog dizajna integriranih krugova. Cilj je napraviti spojnu mrežu takvu da ona zadovoljava sva zadana ograničenja i da su spojevi u skladu sa zadanom mrežnom listom. S obzirom na složenost problema cijelo se područje razbija na više manjih pravokutnih površina koje se nazivaju kanali.

Cilj je pronaći kanal minimalne širine koji je dovoljan za smještaj svih spojeva. Još dodatno je cilj da svi ostali parametri budu minimizirani (duljina puteva, broj spojnih točaka,...)

Za kanal se koristi restriktivni kanal koji je definiran kao kanal s kontaktima na vrhu i na dnu. Prijelazi horizontalnih segmenata između staza nije dozvoljen.

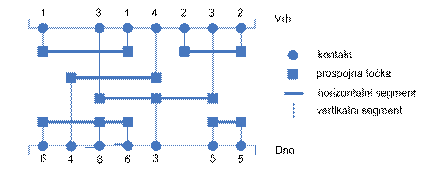
SLIKA 2.16 – Primjer restriktivnog kanala

Horizontalne i veritkalne linije se nalaze u dva odovjena sloja.

Jedan gen u kromosomu predstavlja odnos između dva para spojeva (m,n). Odnosi su slijedeći:

- 0 spoj m mora biti znad spoja n

- 1 spoj n mora biti iznad spoja m

- * nije bitno

Kromosom se gradi kao skup svih mogućih parova (m,n) s odgovarajućim oznakama (0,1,*).

Mreža m	1	1	1	1	1	2	2	2	2	3	3	3	4	4	5
Mreža n	2	3	4	5	6	3	4	5	6	4	5	6	5	6	6
Gen	*	0	0	*	0	0	*	0	*	1	0	0	*	0	*

SLIKA 2.17 – Prikaz kromosoma

Kako bi se skratila duljina kromosoma svi oni označeni s * se izbacuju kao i oni parovi čija bi eventualna promjena položaja ugrozila ograničenja (to se vidi u prikazu mreže grafom koji je obješnjen u članku).

Ovako skraćen kromosom sadržava samo nule ili jedinice i kao takav se može tretirati kao binarni string što znači da se nad njime mogu provoditi operacije križanja i mutacije definirane za binarne stringove. Križanje je klasično s dvije točke prekida, a mutacija jednostavna uz vjerojatnost mutacije p_M.

Funkcija dobrote je vrlo jednostavna i od variajbli uključuje broj zauzetih staza i ukupnu duljinu vertikalnih segmenata koji su u jednom rješenju. Dobrota je bolja što je vrijednost funkcije dobrote manja.

Originalni naslov:

„Genetic Algorithm For Restrictive Channel Routing Problem“

Autori:

Vladimir N. Davidenko, Victor M. Kureichik, Victor V. Miagkikh

Dostupan na:

http://garage.cps.msu.edu/papers/GARAGe97-02-04.pdf

2.18. Za dizajn univerzalnog motora

Kao što je već ranije navedeno genetski algoritmi su „alati“ koji ne zahtjevaju veliko inženjersko znanje kako bi dali dobre rezultate. To omogućuje sam princip genetskih algoritama koji je zapravo jako prilagodljiv problemu. Jedan od alata koji koristi genetske algoritme je GABSys (Genetic Algorithm-Bond Graph System), alat za sintezu više dimenzionalnih dinamičkih sustava pomoću grafova ovisnosti. Ovdje je konkretno prikazan dizajn dvotaktnog motora s unutarnjim izgaranjem dizajniranog pomoću GABSys – a. Sve što inženjer mora napraviti je graf ovisnosti koji predaje programu kao i zahtjeve koje sustav mora zadovoljiti koji se u programu predstavljaju kao funkcija doborte.

Graf ovisnosti opisuje interakciju između dijelova sustava koristeći simbole i linije.

Kromosomi su kodirani parametri dijelova sustava definirani grafom ovisnosti. Konkretno za ovaj primjer motora postoji 15 parametera koji su binarno kodirani pomoću 8 bitova(npr. radijus ulazne cijevi .01 - .256 m, može poprimiti 2⁸ različitih diskretnih vrijednosti). Tako zakodirani parametri prolaze kroz genetski algoritam.

Kao primjer rada dizajnirana su dva motora, jedan od 8 ks i drugi od 20 ks s minimalnom potrošnjom goriva. Dakako da zobg malog broja parametara kao i jednostavnog zahtjeva u funkciji dobrote (samo snaga) rezultati nisu bili optimalni no primjer pokazuje kako su genetski algoritmi sposobni izgraditi ovakvu strukturu koja uz odgovarajući broj parametara i dobro definiranu funkciju dobrote može biti jako kvalitetno rješenje.

Originalni naslov:

„GABSys: Using Genetic Algorithms to Breed a Combustion Engine“

Autori:

B. Danielson, J. Foster, D Frincke

Dostupan na:

http://www.csds.uidaho.edu/deb/bond-icec98.pdf

3. Problem trgovačkog putnika

3.1. Definicija problema

Definicija koja jako dobro opisuje dani problem u njegovoj osnovnoj i najjednostavnijoj varijanti je slijedeća definicija preuzeta iz [6]:

Za dan skup gradova i cijenu putovanja između svakog para gradova, problem trgovačkog putnika (Traveling Salesman Problem, TSP) mora pronaći najjeftiniji put koji će obići sve gradove točno jednom i na kraju se vratiti u početni grad.

U ovom seminarskom radu razmatra se ovakva definicija problema uz uvjet da je cijena putovanja od grada A do grada B jednaka kao i cijena putovanja od grada B do grada A.

Iako je definicija vrlo jednostavna i jasna problem je jako težak, čak štoviše spada u klasu NP - teških problema. Točnije problem je faktorijalne složenosti što u prijevodu znači da za 10 gradova broj mogućih rješenja iznosi 10! = 3,628,800. Ako se ide gledati za veći broj gradova, što su u današnje vrijeme realne ture, 100 – tinjak gradova, broj mogućih tura se penja na približno 9.3e157, što se metodom grube sile (brute force) uz današnju snagu računala ne može riješiti 3e144 godina uz pretpostavku da je broj ruta koje današnje računalo može obraditi po sekundi jednak 1.000.000 [5].

Problem se osim gornje definicije može proširiti dodavanjem različitih ograničenja gornjoj definiciji. Tako je nastao i vremenski ovisan problem trgovačkog putnika, koji uz minimalnu duljinu puta u obzir uzima i vrijeme koje je potrebno da se put obavi kao i eventualne vremenski periodi u kojima se jedan dio posla mora napraviti [2]. Uz ovu defniciju postoji još i asimetrični problem trgovačkog putnika u kojemu put između grada A i grada B nije isti kao i pu između grada B i grada A [2]. Uz ove definicije postoje još i mnoge druge, no njihovo objašnjavanje izlazi iz opsega ovoga rada.

3.2. Genetski algoritmi i problem trgovačkog putnika

Iz definicije problema vidi se da bi genetski algoritmi kao stohastička metoda za pretraživanje mogli biti korisni u rješavanju problema. Zbog načina rada genetski algoritmi ne pretražuju cijeli prostor rješenja već pomoću posebno definiranih operatora križanja i mutacija evoluiraju rješenje. Za praktičnu primjenu genetski algoritmi dobivaju još jedan plus zbog toga što u praksi nije nužno naći optimalni put već je dovoljno dobar put i onaj koji je u okolici optimuma. Također rad algoritma je moguće regulirati i usmjeravati podešavanjem parametara koji su objašnjeni u poglavlju 4.

Uz sve ovo moguće je i kombinirati genetske algoritme s metodama traženja lokalnog optimuma kako bi pojedina jedinka što brže konvergirala prema svom optimumu koji je potencijalno i globalni. Takvi se algoritmi nazivaju hibridnima. Primjer hibridnosti koji je ovdje ostvaren je korištenje 2opt metode kao operatora za mutaciju.

3.2.1. Prikaz kromosoma

Iako postoji više mogućih načina prikaza za ovaj rad odabran je najintuitivniji prikaz koji se može prikazati na slijedeći način:

( 0 , 1 , 3 , 5 , 4 , 6 , 2 , 7 )

U ovom prikazu postoji 8 gradova koje treba obići, a redosljed obilaska je slijedeći: kreće se iz grada 0, pa u grad 1, nakon njega 3 itd. Dakle mjesto u osmorki označava kada će taj grad biti posjećen. A broj koji je na tom mjestu označava sam grad. Ukratko, gradovi su poredani u smjeru u kojem se posjećuju. Ovaj način prikaza je uobičajen u TSP implementacijama. [2,5]

Još jedan način prikaza koji se koristi je matrični prikaz. Matrica je tipa n * n i to je zapravo matrica susjedstva u grafu koji se dobiva povezivanjem svih gradova. Ako postoji put iz grada A u grad B tada je na mjestu M[A,B] jedinica, inače je 0. No zbog kompleksnosti on nije ovdje korišten, iako je po brzini izvođenja bolji prkaz od ovdje korištenog i danas se ide u smjeru razvoja operatora za ovakav način prikaza kromosoma. [2]

3.2.2. Funckija cilja

Funkcija cilja je jednostavna forlmula koja zbraja udaljenosti između gradova, dajući tako za svaki kromosom ukupnu dužinu puta. Naravno, što je dužina puta kraća, kromosom je bolji i ima veću šansu za opstanak.

3.2.3. Operatori selekcije

Prirodna selekcija [4]

Iz početne se populacije eliminira R = M x p_e / 100 jedinki. Jedinke se eliminiraju tako da se sačuva različitost populacije, odnosno eliminiraju se slične jednike. Za početak cijela se populacija sortira prema dobroti. Nakon toga se uspoređuje sličnost dobrota susjednih jedniki i ukoliko je njihova razlika manja od predefiniranog malog realnog pozitivnog broja ε, eliminra se jedna od n – torki. To se ponavlja dok je broj eliminiranih jedniki manji od R. Ako je nakon ovog postupka broj eliminiranih jedinki i dalje manji od R eliminiraju se jedinke s lošijom vrijednošću funkcije dobrote.

Turnirska selekcija [1,3]

Turnirska selekcija je zapravo vrlo jednostavana. Iz cijelokupne populacije odabere se k jedinki (k je veličina turnira, obično između 3 i 7) te se najlošija od njih izbaci. Od ostatka jedniki slučajnim se odabirom odabiru dvije koje se onda križaju i daju novu jedniku koja ulazi na mjesto stare u populaciju.

3.2.4. Operatori križanja

Partially matched crossover (PMX) [2,5]

PMX križanje je vrlo jednostavno, a radi na slijedeći način:

U oba roditelja označe se 2 točke prekida ( na slici 3.1 označene s | ), geni između tih točaka se zamijene u oba roditelja,što daje slijedeće: 3 zamjenjuje 2, 8 zamjenjuje 4, 4 zamjenjuje 1 i obratno.

Sada se popunjava ostatak kromosoma tako da se gradovi izvan točaka prekida vraćaju na svoje mjesto ukoliko već ne postoje kao rezultat zamjene. U tom se slučaju na mjesto grada koji postoji upisuje onaj kojeg mijenja novopridošli grad. Npr. kada se nakon zamjene želi u prvo dijete staviti grad 1 on već postoji (novija jedinica pridošla iz drugog kromosoma). Sada na mjesto jedinice dolazi 8 jer 4 zamjenjuje 1, a kako i 4 već postoji u kromosomu 8 zamjenjuje 4.

(2 5 1 | 3 8 4 | 7 6)

(8 6 7 | 2 4 1 | 3 5)

postaje

(3 5 8 | 2 4 1 | 7 8)

(1 6 7 | 3 8 4 | 2 5)

SLIKA 3.1 – PMX križanje

PMX križanje ima problem jer želi populaciju odvući u lokalni optimum što se mora rješiti korištenjem mutacije.

Greedy crossover [1]

Definicja Greedy Crossover križanja je slijedeća:

„Greedy Crossover uzima prvi grad iz jednog roditelja, uspoređuje gradove u koje se dolazi iz tog grada u oba roditelja te uzima onog čiji je put kraći. Ako se je jedan grad već pojavio u djetetu tada se uzima drugi. Ako su oba u djetetu tada se slučajnim odabirom odabire jedan neodabrani grad.“

Ovo križanje je jako efikasno i brzo skraćuje ture.

Greedy subtour crossover (GSX) [4]

Ovo križanje radi tako da iz oba roditelja uzima što je moguće dulji podskup gradova iz oba roditelja na način koji je prikazan na slici 3.2. Na taj je način najbolje sačuvan genetski materijal roditelja. To zapravo znači slijedeće, ako postoje dva kromosma koja oba sadržavaju podskupove optimalne ture, ovim križanjem se može vrlo brzo doći do spajanja tih dijelova što naravno dovodi do brže konvergencije samog problema.

ulaz: kromosom k_a = (a₀,a₁,..., a_n-1) i k_b= (b₀,b₁,..., b_n-1)

izlaz: dijete k

procedura krizaj (k_a,k_b){

f_a <- true

f_b <- true

izaberi jedan slucajan grad g

izaberi x gdje je a_x= t

izaberi y gdje je b_y= t

k <- t

čini{

x = (x – 1) mod n

y = (y - 1) mod n

ako f_a = true onda{

ako a_x nije u k onda

k <- a_x* k

inače

f_a <- false

}

ako f_b = true onda{

ako b_y nije u k onda

k <- k * b_y

inače

f_b <- false

}

} dok f_a= true ili f_a = true

ako staza nije potpuna onda

dodaj ostale gradove slucajnim redosljedom u k

vrati k

}

SLIKA 3.2 – Pseudokod GSX algoritma, n je broj gradova, a * je znak konkatenacije nizova

Od ovdje opisanih ovo je najefikasnija vrsta križanja.

3.2.5. Operatori mutacije

Jednostavna mutacija [1]

Kao što joj i ime kaže jednostavna mutacija radi tako da uzme dva slučajno odabrana grada u kromosomu i zamjeni njihova mjesta. Na slici 3.3 je prikazana zamjena 5 i 1.

(3 5 4 2 6 1 7 8)

postaje

(3 1 4 2 6 5 7 8)

SLIKA 3.3 – Jednostavna mutacija

Greedy swap mutacija [1]

Ova mutacija je u potpunosti ista kao i jednostavna no uz jedan dodatni uvjet. Do zamjene kromosoma dolazi samo ako je tura dobivena mutacijom kraća od one prije mutacije.

2opt metoda[4]

Ova metoda je jedna od najpoznatijih metoda lokalnog pretraživanja u algoritmima koji rješavaju problem trgovačkog putnika. Unapređuje turu brid po brid i okrećući poredak gradova u podturi. Algoritam je prikazan na slici 3.4, a detaljniji rad algoritma opisuje slijedeći primjer: zamislimo si put od grada A do grada B i put od grada C do grada D. Uspoređuje se da li je AB + CD > AC + BD. Ako je, dolazi do zamjene kao što je to prikazano na slici 3.4. To se ponavlja dok je god moguće skratiti turu. Korištenje ovog operatora unosi hibridnost u implementaciju s obzirom na to da je ovo klasična metoda pretraživanja. Velik problem 2opt metode je zapinjanje u lokalnom optimumu iz kojeg se na može izvući zobg načina usporedbe. Zato su tu opertari križanja koji unose dovoljnu raznolikost kako bi 2opt metoda konvergirala sve do globalnog optimuma. Na usprkos ovog ograničenja ovo je daleko najbolji operator mutacije što se vidi i u poglavlju 4.2 gdje se radi usporedba ovdje opisanih operatora.

SLIKA 3.4 – 2opt metoda

4. Praktični rad

4.1. Rad s aplikacijom

Aplikacija kao i izvorni kod dostupni su na CD – u uz ovaj rad. Programski jezik kroišten za implementaciju ovog algoritma je C#.

Rad s apliakcijom se može predstaviti pomoću slijedećeg dijagrama toka

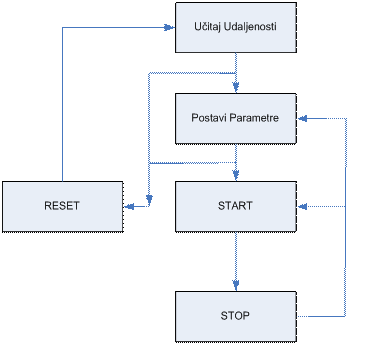
SLIKA 4.1 – Dijagram toka korištenja programa

Učitavanje udaljenosti vrši se na dva načina. Prvi je učitavanje parametara iz XML datkoteke formata prikazanog na slici 4.2. Prilikom ove vrste učitavanja programu su potrebne dvije vrste podataka. Prva je broj gradova, a druga su koordinate svih gradova.

Ova vrsta učitavanja je kompatiblina s velikom kolekcijom gotovih problema dostupnih na Webu.

Drugi način učitavanja točaka je jednostavno postavljanje točaka mišem po ekranu nakon kojeg pritiskom na tipku „učitavanje udaljenosti“ program sam odredi koordnate postavljenih točaka.

<TSP>

<info>

</info>

<tocke>

</tocke>

</TSP>

SLIKA 4.2 – Zapis ulazne datoteke

Unutar tag-ova <brojGradova> upiše se veličina problema, dok se unutar tag-ova <tocke> upisuju koordinate gradova (x i y koordinata).

Nakon što se učitaju udaljenosti slijedi postavljanje raznih vrsta parametra, od vrsta genetsikh operatora do ograničenja za te operatore. Parametri koji se mogu postvljati su slijedeći:

- veličina populacije

- uvjet zaustavljanja – može biti ili broj generacija ili broj generacija koji mora proći s istom najboljom jedinkom

- vrsta selekcije, zajedno s odgovarajućim parametrima. Kod prirodne selekcije to su vjerojatnost selekcije i epsilon, dok su kod turnira to vjerojatnost selekcije i veličina turnira.

- vrsta križanja, ovdje je bitno reći da je vjerojatnost križanja jednaka vjerojatnosti slekcije zobg načina na koji selekcije djeluju na populaciju.

- vrsta mutacije i vjerojatnost mutacije.

Nakon postavljenih parametara algoritam može započeti s radom, a sama kontrola rada vrši se s tipkama „start“, „stop“ i „reset“. Pritiskom na tipku „start“ pokreće se rad algoritma, pritiskom na tipku „stop“ rad se zaustavlja, no problem ostaje učitan što omogućuje korisniku ponovno rješavanje problema s novim ili istim parametrima. Tipka „reset“ služi za poništavanje svih vrijednosti, od parametara do učitanog problema.

4.2. Rezultati i usporedbe rada genetskih operatora

Računalo na kojem su izvođeni testovi je Intel Pentium IV 450 MHz s 256 MB RAMa pod Microsoft Windows XP SP2 operativnim sustavom s .NET Frameworkom 1.1.

Nakon niza testova s različitim parametrima pokazalo se da je najbolja kombinacija operatora slijedeća:

- prirodna selekcija

- Greedy Subtour crossover

- 2opt meoda za mutaciju

Korištenjem ovih operatora algoritam je svaki puta došao do optimalnog rješenja i to svega u par generacija. Problemi koji su korišteni za prikaza rada algoritma su bayg29 i att48. To su standardni problemi za testiranje rada aplikacija koje rješavaju problem trgovačkog putnika čija je optimalna ruta poznata, a njihove XML datoteke su dostupne uz izvorni kod programa, kao i optimalne rute.

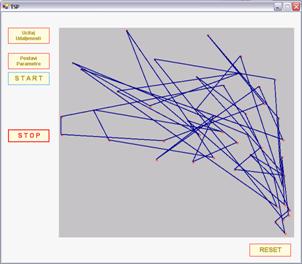
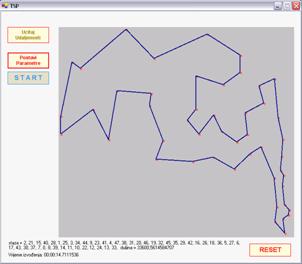
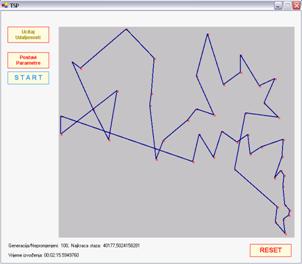
SLIKA 4.3 – rezultati izvođenja algoritma korištenjem predefiniranih postavki, lijevo je početno stanje, a desno je optimalna ruta. Testni problem je att48.

Vrijeme potrebno za pronalazak optimalne rute uz predefinirane postavke je 14.711 sekundi, uzeto kao srednje vrijeme 5 izvođenja s istim postavkama. Postignuto je optimalno rješenje uz brzu konvergenciju ka njemu. Optimalna ruta nalazi se u datoteci att48.opt.tour.

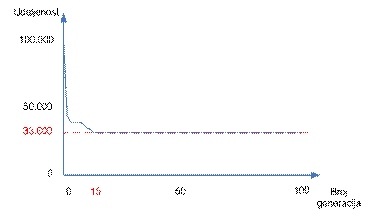
SLIKA 4.4 – Konvergencija rješenja, crvenim slovima su prikazane najkraća udaljenost kao i generacija u kojoj je postignuta ta udaljenost

Graf na slici 4.4 treba uzeti s rezervom zbog prirode genetskih algoritama, odnosno zbog načina na koji oni dolaze do rješenjena. Koji put će prije konvergirati ka rješenju, a koji put kasnije.

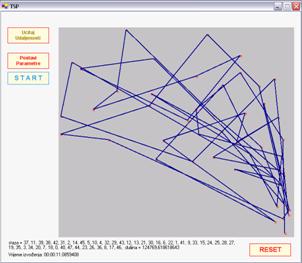
SLIKA 4.5 – „Optimalna“ ruta nakon 100 generacija određena korištenjem prirodne selekcije, PMX križanja i jednostavne mutacije i predefiniranih postavki.

Kao što se vidi iz slike 4.5 rezultati korištenjem prirodne selekcije, PMX križanja i jednostavne mutacije uz predefinirane postavke znatno su lošiji nego oni korištenjem operatora sa slike 4.3. Duljina staze je 124.769 što je 4 puta lošije rješenje od optimalnog.

Uz promjenu parametra, to jest uz njihovo postavljanje na agresivnije postavke postignuti su slijedeći rezultati.

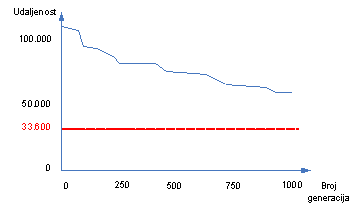
SLIKA 4.6 – Konvergencija s promjenjenim parametrima

Postavke parametara su slijedeće:

- broj generacija = 1000

- vjerojatnost križanja = 55 %

- epsilon = 200

- vjerojatnost mutacije = 35 %

Ostali parametri su nepromjenjeni. Uz ove postavke vrijeme izvođenja algoritam penje se na preko dvije minute, rezultat je duplo bolji od prethodnog i iznosi 59600, što je još uvijek duplo lošije od optimalnog rješenja postignutog korištenjem predefiniranih postavki.

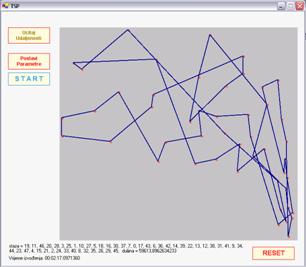
Na slici 4.7 korištena je turnirska selekcija, greedy crossover križanje i greedy swap mutacija. Korišteni parametri su i u ova dva slučaja predefinirani. Vrijeme izvođenja algoritam bilo je nešto manje od dvije i pol minute. Duljina puta koja je pri tome postignuta iznosi 40177 što je usporedivo s optimalnom rutom.

SLIKA 4.7 – Optimalna ruta nakon 100 generacija korištenjem turnira veličine 5, greedy croosover križanja i greedy swap mutacije

Uz malo agresivinije postavke parametara ili povećanje broja generacija došlo bi se i do optimalne rute. Iz ova četiri primjera vidljivo je kako se za različite operatore i za različite postavke parametara algoritam potpuno drugačije ponaša. Iz toga se vidi velika važnost svih komponenti koje čine genetski algoritam i koliko je važno da se svakom dijeli algoritma pri dizajnu dodjeli jednaka pažnja kako bi on davao što bolje rezultate.

Direktne usporedbe rada pojedinih genetskih operatora iste namjene

Za ove usporedbe korišten je problem bayg29, čija je datoteka, zajedno s optimalnom turom također dostupna uz aplikaciju. Ove usporedbe su rađene tako da se jedna vrsta operatora mijenja dok druga dva ostaju konstanta kao bi se direktno moglo vidjeti kako pojedini operator djeluje na rad algoritma, što vremenski, što gledajući konvergenciju problema. Parametri algoritma su postavljeni na predefinirane vrijednosti.

Prva usporedba je usporedba prirodne selekcije i turnirske selekcije. Operator križanja je GSX, a operator mutacije je Greedy Swap mutacija. Duljina optimalne rute iznosi 9074. Bitno je napomenuti da bu uz druge operatore križanja i selekcije rezultati bili drugačiji, moguća su znatna odsutpanja od ovdje prikazanih. Razlog zašto nisu rađene sve međusobne usporedbe operatora je broj mogućih kombinaicja, koji je 18.

	Vrijeme izvođenja	Duljina ture
Prirodna selekcija	8,5 sekundi	13594
Turnirska selekcija	58 sekundi	10358

SLIKA 4.8 – Usporedba operatora selekcije

Iz slike 4.8 se vidi kako je prirodna selekcija puno brži operator, no daje slabije rezultate, dok su turniri znatno sporiji iako daju rezultata koji je znatno bliži optimumu.

	Vrijeme izvođenja	Duljina ture
GSX križanje	5,8 sekundi	13016
Greedy Crossover	7,6 sekundi	9854
PMX križanje	4,9 sekundi	16864

SLIKA 4.9 – Usporedba operatora križanja

Iz slike 4.9 vidi se kako je korištenje greedy crossover – a dalo najbolji rezultat uz srednji potrošak vremena. PMX križanje, iako je najbrže dalo je jako loš rezultat, odnosno brzo je zaglavilo u lokalnom optimumu iz koje se nije moglo izvući. GSX križanje je brzo, a daje i srednji rezultat zbog čega je u kombinaciji s 2opt metodom najbolja postavka algoritma što se pokazalo kroz dodtna testiranja. Korištena je prirodan selekicja i Greedy Swap mutacija.

	Vrijeme izvođenja	Duljina ture
Jednostavna mutacija	5,9 sekundi	15500
Greedy Swap mutacija	6,3 sekunde	15800
2opt metoda	4,99 sekunde	9074

SLIKA 4.10 – usporedba operatora mutacije

Slika 4.10 pokazuje kako je 2opt metoda daleko najbolji operator mutacije i vremeski i po rezultatu, već u trećoj generaciji je pronađen globalni optimum. No to niti ne začuđuje zbog načina na koji 2opt metoda vrši pretraživanje. Troši malo procesorskog vremena, a unapređuje rutu dok je to god moguće. Druge dvije mutacije daju usporedive rezultate što je isto tako očekivano s obzirm na njihove načine rada koji su jako slični. Selekcija je i u ovom slučaju prirodna, dok je za križanje korišten GSX.

Vremenske testove treba treba uzeti s određenom rezervom zbog toga što se jedan dio vremena troši na crtanje svake nove najbolje rute dok algoritam traži optimalno rješenje. Nasuprot toga rezultati vezani uz pronalaske „optimalnih“ ruta su puno realniji te se kroz njih vidi kako je koji operator dobar. Naravno uz promjene parametara neki durgi operatori mogu postati bolji. Sve zavisi od problema koji se rješava. Također, određene komibnacije operatora daju odlične rezultate dok pak neke druge kombinacije daju jako loše rezultate.

Zaključak

Kroz opise primjena genetskih algoritama vidi se kako je njihova primjena već vrlo široka i kako postoje razne varijante genetskih algoritama, svaka varijanta za svoj problem. Iz toga se može izvući još jedan zaključak o genetskim algoritmima, a to je da su oni zapravo samo princip, ideja, smjernica kako neki problem rješiti na drugačiji način od klasičnih metoda, jer je sve na korisniku da se sam odluči da li će razvijati svoj vlastiti algoritam ili će probati svoj problem prilagoditi već nekom postojećem algoritmu koji rješava neku sličnu klasu problema.

Također, vidi se da su genetski algoritmi korisni za one klase problema koje se ne mogu rješiti na klasične načine. Iako po brzini nisu u vrhu, po veličini područja koje pretražuju su vjerovatno daleko bolji od svih ostalih metoda. To se jako dobro vidi na primjeru problema trgovačkog putnika, čiji je prostor rješenja ogroman već i za stotinjak gradova.

Praktični rad je pokazao kako je jedna od najbitnijih stvari za uspješan rad algoritma ispravan odabir genetskih operatora kao i parametara koji će odrediti ponašanje tih operatora. Ako se oni ispravno odrede algoritam daje fantastične rezultate, no ako se je nijhov odabir nesmotren algoritam će najvjerojatnije završiti rad u nekom lokalnom optimumu, bliže ili dalje od pravog optimuma, ovisno o parametrima.

Literatura

[1] Konstantin Boukreev. “Genetic Algorithm and Traveling Salesman Problem”,

http://www.generation5.org/content/2001/tspapp.asp, 2001.

[2] Kylie Bryant, Arthur Benjamin. “Genetic Algorithms and the Traveling Salesman Problem”,

http://www.math.hmc.edu/seniorthesis/archives/2001/kbryant/kbryant-2001-thesis.pdf, 2000.

[3] Marin Golub, doc. dr.sc. “Genetski algoritam”, http://www.zemirs.fer.hr/~golub/ga.html, 2004.

[4] Hiroaki Sengoku, Ikua Yoshihara. “A Fast TSP Solver Using GA on Java”

http://www.gcd.org/sengoku/docs/arob98.pdf, 1998.

[5] Andy Thomas. “Solving The Travelling Sales Man Problem Using Genetic Algorithm”, http://www.generation5.org/content/2001/ga_tsp.asp, 2001.

[6] http://www.tsp.gatech.edu/problem/index.html