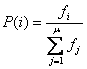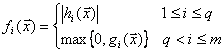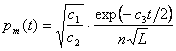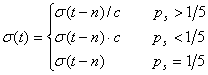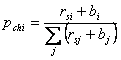1. Uvod

Evolucijski algoritmi su algoritmi inspirirani biološkom evolucijom, primjenjivi na širok skup problema. Pojavili su se već u pedesetim godinama 20. stoljeća, te ih se neprestano razvija sve do danas. Prednost te klase algoritama je u tome što ih je moguće primijeniti u slučajevima kad ne postoji neka unaprijed određena, jasno definirana metoda za rješavanje nekog postupka ili postojeće metode imaju preveliku složenost. Jedan primjer za to je traženje optimuma funkcije više varijabli čiji analitički oblik nije poznat. Optimum bi se mogao pronaći uz iscrpnu pretragu svih mogućih kombinacija vrijednosti varijabli, međutim, takav postupak naprosto traje predugo. Nadalje, svi evolucijski algoritmi, s naglaskom na genetske algoritme na koje je ovaj rad orijentiran, imaju određene parametre koje je potrebno podesiti prije pokretanja algoritma. Podešavanje vrijednosti tih parametara je iscrpan i dugotrajan postupak, pa se stoga vrijednosti tih parametara nastoji podešavati tijekom rada algoritma. Ovo se naziva upravljanje parametrima. Kada se u postupku upravljanja parametrima koristi informacije o stanju pretrage, onda se takvo upravljanje naziva adaptivnim. Ovaj se rad zasniva na genetskim algoritmima koji su podskup evolucijskih algoritama, te na adaptivnom upravljanju parametrima.

Evolucijski algoritmi opisani su u 2. poglavlju, kao i genetski algoritmi kao njihov podskup. Pokazana je ideja iza evolucijskih algoritama, te su opisane njihove glavne sastavnice i njihov rad ilustriran na primjeru. Potom su pobliže opisani genetski algoritmi, te detaljno klasificirani njihovi sastavni dijelovi, te se dani primjeri za svaku skupinu. Tu su opisani operatori mutacije, rekombinacije i selekcije, te prikaz rješenja i oblici evaluacijskih funkcija. Objašnjeno je kad ima smisla koristiti pojedine operatore i za koje su tipove problema pojedini operatori pogodni.

U 3. poglavlju dan je pregled nekih postojećih metode upravljanja parametrima. Na početku je prikazana jedna od ponuđenih podjela upravljanja parametrima genetskog algoritma. Na temelju nje su podijeljeni pojedini pododjeljci koji se bave adaptivnim mehanizmima u pojedinim dijelovima genetskog algoritma. Na početku su prikazane metode upravljanja parametrima kod evaluacijske funkcije i opisano je kad se one najčešće koriste. Potom su opisane metode vezane uz rekombinaciju, mutaciju, selekciju i veličinu i oblik populacije. Iz svake su skupine dani samo karakteristični primjeri mehanizama upravljanja parametrima, s obzirom da ih u praksi ima mnogo i nije ih moguće u okviru ovog rada sve pobrojati.

U 4. poglavlju opisano je jedno ostvarenje genetskog algoritma – turnirski genetski algoritam koji rješava problem trgovačkog putnika. Opisana je implementacija turnirskog genetskog algoritma. Prikazani su i neki genetski operatori specifični za problem trgovačkog putnika koji su implementirani za potrebe ovog rada. Naposljetku, obavljen je niz eksperimenata na nizu instanci problema trgovačkog putnika sa svrhom nalaženja optimalnog skupa parametara za rad našeg genetskog algoritma. Navedene su inačice problema opisane, kao i korišteni skupovi parametara za genetski algoritam, te su naposljetku opisani i komentirani rezultati eksperimenata.

5. poglavlje opisuje neke nove adaptivne metode upravljanja parametrima razvijene posebno za potrebe ovog rada, a koje se zasnuju na parametru vjerojatnosti mutacije i izmjeni operatora mutacije. Opisani su provedeni eksperimenti, te je rezultatima pokazano da naše adaptivne metode zaista rade i da genetski algoritam koji ih rabi radi bolje od onog opisanog u 4. poglavlju.

2. Evolucijski algoritmi

2.1. Evolucijski algoritmi

Evolucijski algoritmi spadaju u kategoriju stohastičkih izgeneriraj i isprobaj (generate&test) algoritama koji pretražuju prostor stanja koristeći neku heuristiku kojom ocjenjuju kvalitetu rješenja. Evolucijski su algoritmi širi pojam i obuhvaćaju genetske algoritme, evolucijske strategije, genetsko programiranje i evolucijsko programiranje [1].

Evolucijski je algoritam u načelu primjenjiv na bilo kakav problem uz dvije pretpostavke. Prva je pretpostavka da za rješenje problema postoji neki prikaz. Primjerice, ako je problem nalaženje optimuma realne funkcije od pet varijabli, tad je rješenje moguće prikazati kao peterodimenzijski vektor s realnim komponentama. Ako je problem nalaženje redoslijeda obilaska gradova u problemu trgovačkog putnika, tada je rješenje moguće prikazati kao permutaciju rednih brojeva gradova. No, permutacijom rednih brojeva gradova moguće je opisati i redoslijed obilaska gradova koji nije najkraći mogući, kao što je vektorom moguće opisati i točke koje nisu rješenja problema nalaženja optimuma funkcije. Druga je pretpostavka da postoji heuristika za ocjenu kvalitete pojedinog rješenja. U slučaju nalaženja optimuma funkcije, to može biti vrijednost funkcije, a u slučaju problema trgovačkog putnika, to može biti duljina puta za odabrani redoslijed obilaska gradova (što je duljina puta manja, to je rješenje kvalitetnije).

Evolucijski algoritam na početku svog rada slučajnim odabirom ili nekim heurističkim postupkom odabere neki skup rješenja s pripadnim prikazom. Potom iz tog skupa rješenja odabire ona najbolja u skladu heuristikom kvalitete rješenja, te na temelju njih stvara nova, u nekoj mjeri izmijenjena rješenja koja služe za sljedeću iteraciju algoritma. Iteracije se ponavljaju sve dok se ne zadovolji neki uvjet zaustavljanja.

Pritom, rješenja se nazivaju jedinkama (individuals), heuristiku za ocjenu kvalitete rješenja evaluacijskom funkcijom (evaluation function), a pojedine iteracije algoritma generacijama (generation). Skup rješenja u pojedinoj generaciji naziva se populacija (population). Rješenja na temelju kojih se stvaraju nova nazivaju se roditelji (parents), a novostvorena rješenja su njihova djeca (children) ili potomci (offspring). Najčešće postoje dva mehanizma pomoću kojih se stvaraju izmijenjeni pojedinci, a to su rekombinacija (rekombinacija), ili križanje (crossover), i mutacija (mutation).

Treba primijetiti, iz gornjeg opisa, da u radu evolucijskog algoritma postoje dva mehanizma koja služe za pronalazak rješenja. Prvi mehanizam čine rekombinacija i mutacija, koje osiguravaju da u populaciji jedinki postoji raznolikost, te da se pojavljuju nove jedinke. Drugi, oprečni, mehanizam je selekcija boljih pojedinaca, koja osigurava veću ili jednaku kvalitetu jedinki u svakoj narednoj generaciji. Ideja je u tome da se pojedinci s višom vrijednošću evaluacijske funkcije s većom vjerojatnošću biraju za prijelaz u sljedeću generaciju, ili da budu roditelji za nove, njima slične, jedinke.

Nije teško zamijetiti povezanost evolucijskih algoritama s evolucijom živih bića u kojoj pronalazak rješenja na problem (zapravo, organizma koji je najbolje prilagođen okolišu) određuju prirodna selekcija, te povremene mutacije (promjene na genotipu). Zbog te se povezanosti u evolucijskom računarstvu često posuđuje terminologija iz genetike i evolucije.

U sljedećem će odlomku biti razmotren pseudokod evolucijskog algoritma. Potom su opisane osnovne sastavnice evolucijskih algoritama, nakon čega je dan primjer rada jednog evolucijskog algoritma.

2.1.1. Pseudokod evolucijskog algoritma

U prošlom je odjeljku dan ilustrativan prikaz rada evolucijskog algoritma. U ovom je odjeljku naveden pseudokod njegovog rada, te su pritom izdvojeni ključni dijelovi evolucijskog algoritma. Slika 2.1. prikazuje općenit pseudokod evolucijskog algoritma.

Slika 2.1. Pseudokod evolucijskog algoritma

Već je spomenuto da je prikaz rješenja ključna pretpostavka evolucijskog algoritma, što je prva bitna sastavnica evolucijskog algoritma. Nadalje, već je navedeno da evolucijski algoritam najprije inicijalizira populaciju jedinki. Potom se svaka od jedinki evaluira, tj. dodijeljuje mu se vrijednost evaluacijske funkcije, nakon čega počinje glavni ciklus evolucijskog algoritma – nekim se postupkom odabiru najbolji roditelji, nad njima se obavlja rekombinacija kako bi se dobile nove jedinke, koje se s nekom vjerojatnošću mutiraju, te se naposljetku odabiru jedinke za sljedeću generaciju na temelju evaluacijske funkcije. Treći se korak ponavlja sve dok se ne ispune uvjeti zaustavljanja. Svi bitni sastavni dijelovi su na slici masno otisnuti, a podrobnije opisani u sljedećem odjeljku.

2.1.2. Sastavni dijelovi evolucijskog algoritma

Prvi korak u definiranju evolucijskog algoritma je povezivanje sa stvarnim svijetom, tj. nalaženje prikaza za jedinke. Rješenje problema u originalnom problemu naziva se fenotip (phenotype), dok se njegovo kodiranje potrebno za rad evolucijskog algoritma zove genotip (genotype). Tako je u problemu nalaženja optimuma funkcije genotip upravo vektor koji predstavlja pojedinu točku, a fenotip je točka kao pojam. Razlika između genotipa i fenotipa, međutim, nije uvijek ovako izravna. Npr. u problemu nalaženja programa koji obavlja neku zadaću (fenotip), prikaz programa (genotip) je najčešće sintaksno stablo. Bitno je napomenuti da se genotip najčešće sastoji od više atomarnih građevnih dijelova, kao što su to u slučaju vektora njegove komponente, a u slučaju stabla njegovi čvorovi. Ti atomarni građevni dijelovi se ponekad nazivaju alele (allele).

Uloga evaluacije je da daje ocjenu kvalitete jedinki. Njena je glavna uloga u odabiru jedinki za sljedeću generaciju ili za stvaranje novih jedinki, pri čemu bolje jedinke dobivaju bolju ocjenu – na taj način evaluacijska funkcija doprinosi poboljšanjima. U evolucijskom se računarstvu ona često naziva funkcija prikladnosti (fitness function).

Mehanizam odabira roditelja (parent selection) služi za odabir jedinki koje će poslužiti za generiranje novih, a zasniva se na primjeni vrijednosti evaluacijske funkcije. U evolucijskom računarstvu je odabir roditelja najčešće stohastički, što znači da jedinke s većom vrijednošću evaluacijske funkcije imaju veću vjerojatnost da budu odabrane za roditelje, no to ne isključuje mogućnost odabira jedinki s manjom kvalitetom. Razlog za ovo je težnja da se izbjegne pohlepnost pretraživanja i smanji mogućnost da populacija jedinki zaglave u lokalnom optimumu.

Za stvaranje novih jedinki u evolucijskim su algoritmima zaduženi varijacijski operatori (variation operators), a to su rekombinacija i mutacija. Rekombinacija uzima dva ili više roditelja i na temelju njih generira jedno ili više rješenja djece. Pritom su neki dijelovi izgenerirane jedinke (neke alele) preuzeti od jednog roditelja, a neki od drugog, što je uvjetovano slučajnim odabirom, pa se kaže da je rekombinacija stohastički operator. Smisao rekombinacije je lokalno pretraživanje, s obzirom da ono kombinira karakteristike više jedinki. Ovo se može jednostavno ilustrirati u problemu nalaženja optimuma funkcije. Naime, jedan od operatora rekombinacije je aritmetička rekombinacija koja za dva dana realna vektora daje vektor čije su komponente aritmetička sredina komponenti vektora roditelja. U slučaju traženja optimuma funkcije, to kao novu jedinku daje točku koja se nalazi na polovici puta između točaka roditelja. Na taj način ovaj operator pretražuje lokalni prostor između postojećih jedinki u potrazi za optimumom.

Mutacija se primjenjuje na novonastale jedinke nakon rekombinacije i to s nekom vjerojatnošću. Slično kao i kod rekombinacije, alela koja se kod jedinke mijenja odabire se slučajno. Mutacija u pretraživanje unosi raznolikost u populaciju jedinki, i obavlja ulogu potpunog pretraživanja.

Treba primijetiti da je stvaranje djeteta zapravo ulazak u novu točku u prostoru pretraživanja. Da bi se pronašlo rješenje, bitno je da prostor rješenja bude povezan (u smislu da postoji operacija čijom je uzastopnom primjenom na neku jedinku moguće izgenerirati bilo koju jedinku u prostoru rješenja), a mutacija može garantirati povezanost prostora rješenja [1].

Odabir preživjelih jedinki (survivor selection) je sličan odabiru roditelja, no on se poziva tek nakon što se izgeneriraju potomci. Kako je u većini slučajeva veličina populacije konstantna, nužno je napraviti odluku o tome koje će jedinke ući u sljedeću generaciju. Kriterij za odabir jedinki je najčešće vrijednost evaluacijske funkcije, iako je moguće koristiti i druge kriterije, primjerice, starost jedinki mjerenu u broju generacija. Dok je odabir roditelja najčešće po prirodi stohastički, odabir preživjelih jedinki je često deterministički.

Inicijalizacija je najčešće jednostavna – početni kandidati za rješenje problema odabiru se nasumično, ili koristeći neku heuristiku karakterističnu za dani problem. Uvjeta zaustavljanja ima više. Ako problem ima poznatu vrijednost funkcije prikladnosti za optimalna rješenja problema, tad je moguće zaustaviti pretraživanje kad se pojavi jedinka koja je dovoljno blizu toj vrijednosti. Međutim, zbog stohastičke prirode evolucijskih algoritama, nema garancije da će ova razina ikada biti dostignuta, pa je nužno dodati neke kriterije zaustavljanja za koje je sigurno da će se prije ili kasnije ispuniti. Takvi kriteriji su najveći mogući broj generacijskih ciklusa, dovoljno mala promjena u najboljoj vrijednosti funkcije prikladnosti u zadnjih nekoliko ciklusa, ili pad raznolikosti populacije ispod nekog praga.

2.1.3. Primjer rada evolucijskog algoritma

U ovom je odjeljku ilustriran rad jednog evolucijskog algoritma. Kao problem je odabrana optimizacija funkcije od dvije varijable na ograničenom intervalu. Poznato je da, u slučaju da je analitički oblik funkcije poznat, postoje precizne matematičke metode za rješavanje ovog problema, međutim, svrha ovog primjera je ilustrativna.

Slika 2.2. Primjer rada evolucijskog algoritma

Evolucijski algoritam inicijalizaciju obavlja odabirom nasumičnih jedinki iz intervala. Veličina populacije je 6. Kao funkcija prikladnosti koristi se funkcija čiji se optimum traži, s obzirom da njena veća vrijednost označava i bolju jedinku. Odabir roditelja obavlja se tako da se naprosto odabere dvije trećine jedinki s najvišom funkcijom prikladnosti. Operator rekombinacije uzima dvije jedinke i vraća jedno čije su komponente aritmetička sredina komponenti jedinki roditelja. Operator mutacije primijenjuje se s nekom malom vjerojatnošću i nasumično mijenja vrijednost jedne komponente vektora rješenja na neku vrijednost iz uniformne distribucije po intervalu na kojem se traži maksimum funkcije. Odabir preživjelih jedinki obavlja se tako da se naprosto odabere 6 najboljih jedinki. Uvjet zaustavljanja je da je prošao neki unaprijed određen broj generacija.

Slika 2.2. prikazuje funkciju dvije varijable na ograničenom intervalu i rad algoritma čiji je cilj naći njen maksimum. Na slici lijevo gore je inicijalna populacija jedinki. Vidljivo je da jedinke na donjem dijelu slike neće biti izabrane za roditelje zbog niske vrijednosti funkcije prikladnosti. Iz gornjih će se parova jedinki izgenerirati dva nova operatorom rekombinacije (pune strelice), a na jedno od djece će djelovati operator mutacije (iscrtkana strelica), i u ovom slučaju dati negativan rezultat, smanjujući kvalitetu rješenja, kao što se vidi na slici gore desno. Ta će jedinka u sljedećoj generaciji biti odbačena zbog niske prikladnosti. Jedinke odbačene zbog niske vrijednosti funkcije prikladnosti prikazane su blijedim tonom. U sljedećoj će se generaciji operator mutacije pokazati korisnim, pomaknuvši jednu od jedinki “uzbrdo”. Naposljetku, nakon većeg broja generacija, jedinke će se grupirati oko optimuma funkcije kao što je prikazano na slici dolje desno.

Treba primijetiti da, iako je postignut globalni optimum, neke su jedinke ostale grupirane oko lokalnog, pa se, zbog stohastičke prirode algoritma (u ovom slučaju, zbog inicijalizacije i operatora mutacije), moglo desiti da nakon isteka nekog broja generacija jedinke ostanu zarobljene oko lokalnog optimuma, te da pravo rješenje uopće ne bude pronađeno. Ta se pojava naziva preuranjena konvergencija (premature convergence). Općenito nije poznat analitički oblik funkcije, ni položaj njenih optimuma, pa u radu evolucijskog algoritma postoji opasnost da jedinke budu zarobljene oko lokalnog optimuma. Postoji čitav niz tehnika koje nastoje riješiti ovaj problem, a neke od njih će biti spomenute kasnije.

2.2. Genetski algoritmi

U ovom će podpoglavlju biti opisani genetski algoritmi. Genetski algoritmi su jedan od podtipova evolucijskih algoritama, a prvi ih spominje John Holland. Danas se pretežno koriste za aproksimaciju funkcija i kao optimizacijske metode, međutim, mogu se primijeniti na niz problema.

Ono po čemu se tipovi evolucijskih algoritama razlikuju su njihovi sastavni dijelovi, pa su njihove inačice temeljito proučene u sljedećim odjeljcima.

2.2.1. Prikaz rješenja

U ovom su odjeljku opisana četiri temeljna prikaza rješenja kod genetskih algoritama. U skladu s tim, pojedini će varijacijski operatori biti kategorizirani prema prikazu kod kojeg se koriste. Treba napomenuti da se u praksi ova četiri prikaza, kao i pripadni operatori, kombiniraju kako bi se prirodnije i prikladnije opisala rješenja problema.

Bitovni niz. Najjednostavniji (i najranije uveden) prikaz je niz bitova. Niz bitova može predstavljati niz istinosnih vrijednosti, ali grupacije bitova isto tako mogu predstavljati cijele brojeve iz nekog intervala. U tom slučaju se javlja problem da različiti bitovi imaju različite težine, što je nepovoljno, s obzirom da neki operatori mutacije naprosto invertiraju vrijednost nasumično odabranog bita. Nuspojava toga je da promjena vrijednosti najznačajnijeg bita dovodi do puno veće promjene u genotipu nego promjena vrijednosti manje značajnog bita. Navedeni se problem rješava Grayevim kodom, kod kojeg je Hammingova udaljenost između bilo koja dva uzastopna cijela broja jednaka 1, pa je promjena vrijednosti nekog od bitova dovodi do manjih promjena u prostoru rješenja.

Cjelobrojni vektor. Cjelobrojni je prikaz pogodniji za slučajeve kad skup cijelih brojeva iz kojeg alele smiju imati vrijednosti nije ograničen. Pri osmišljavanju varijacijskih operatora je kasnije moguće uzeti u obzir vezu između pojedinih cijelih brojeva. Ako cjelobrojna alela predstavlja ordinalnu vrijednost[1], varijacijski operatori to mogu uzeti u obzir; u protivnom isti varijacijski operatori ne moraju davati željene rezultate.

Realni vektor. Prikaz s realnim vrijednostima spomenut je već ranije, u kontekstu nalaženja optimuma funkcije realnih varijabli. Pritom napomenimo još jednom da funkcije ne moraju imati poznati analitički oblik, a i da nisu sve funkcije derivabilne. U tim slučajevima ima smisla koristiti genetski algoritam, i vektor realnih vrijednosti za prikaz rješenja.

Permutacija. Naposljetku, prikaz u obliku permutacije je pogodan za probleme u kojima treba pronaći neki optimalni poredak. Primjeri za to su problem trgovačkog putnika, problem kineskog poštara, problem stabilnog braka (stable marriage problem) ili problem dodjeljivanja (assignment problem). Budući da se u permutaciji vrijednosti ne smije desiti da se bilo koja od vrijednosti ponovi, očito je da se za ovaj prikaz moraju definirati potpuno novi varijacijski operatori, kako bi se u novogeneriranim jedinkama to svojstvo održalo. Pritom treba napomenuti da se permutacijama mogu prikazati dvije klase problema. Prva od njih je ona kod koje je bitan poredak elemenata u permutaciji, kao npr. problem dodjeljivanja. Kod druge je bitno susjedstvo pojedinih elemenata u permutaciji, za što je primjer problem trgovačkog putnika.

Uz standardni prikaz permutacije putem niza brojeva koji se ne smiju ponoviti, postoji i tzv. kodiranje slučajnim brojevima (random key encoding), opisano u [2]. U ovom prikazu jedinke se prikazuju realnim vektorom. O kojoj se konkretno permutaciji radi određuje se sortiranjem vrijednosti u vektoru i na taj način određujući koji element permutacije određena realna vrijednost u vektoru predstavlja. Primjerice, vektor predstavlja permutaciju . Ovaj je prikaz koristan, jer omogućava da se niz već razvijenih operatora za realne prikaze upotrijebi za permutacijske probleme.

2.2.2. Evaluacijska funkcija

Druga bitna komponenta genetskog algoritma je evaluacijska funkcija. Bez evaluacijske funkcije nije moguće ocijeniti kvalitetu pojedine jedinke, pa je ona ključna za rad genetskog algoritma. Ona je osnovica za selekciju i stoga je zaslužna za uvođenje poboljšanja u populaciju. Drugi naziv za nju je funkcija prikladnosti (fitness function), te se obično koristi kod maksimizacijskih problema. Kod nekih problema, kao npr. traženja optimuma višedimenzionalne funkcije, postoji tzv. funkcija cilja (objective function), koja predstavlja funkciju iz problema, pa ta dva pojma treba razlikovati. Kod problema kod kojih postoji funkcija cilja, evaluacijsku funkciju moguće je dobiti izravno ili uz malu transformaciju.

Kod optimizacijskih problema, evaluacijsku je funkciju lako naći. Kod aproksimacijskih problema, za evaluacijsku se funkciju često uzima neka mjera udaljenosti od željenog rješenja. Npr. kod aproksimacije funkcije, može se uzeti srednja kvadratna pogreška (mean square error) te se njena vrijednost minimizirati. Pri treniranju neuronskih mreža, evoluiranju strategija za rješavanje nekog problema ili razvoju inteligentnih agenata, jedinku je moguće naprosto pustiti da rješava neki problem i ocijeniti je na temelju toga koliko se dobro s njim nosi. Primjerice, strategiju za predviđanje uspješnosti poduzetnika koji pokreće neko poduzeće moguće je ocijeniti na temelju uspješnosti njenog predviđanja za veći broj poduzetnika.

Priroda nekih problema je takva da ne postoji mjera kojom bi se mogla odrediti evaluacijska funkcija. Dobar primjer za to je dan u [2], gdje se evoluira populaciju simuliranih svemirskih brodova čije su konfiguracije predstavljene znakovnim nizovima. Cilj je naći svemirski brod koji, u skladu s unaprijed određenim pravilima bitke, može pobijediti što više drugih konfiguracija svemirskih brodova. Primjer je zanimljiv iz razloga što ne postoji unaprijed određena mjera za evaluacijsku funkciju, već se kvaliteta pojedine jedinke određuje isključivo na temelju simuliranih borbi s drugim jedinkama koje su trenutno u populaciji, dakle u odnosu na trenutno stanje u populaciji.

2.2.3. Rekombinacija

Kod genetskih se algoritama nakon odabira roditelja obavlja rekombinacija i to najčešće između dva roditelja. Zbog nadahnuća iz biologije, rekombinacija se često naziva još i križanje (crossover). Križanje se kod genetskih algoritama ne primijenjuje uvijek. Nakon što su odabrani roditelji, iz uniformne se razdiobe u intervalu izvlači vrijednost, te se, ako je ona manja od unaprijed definirane vrijednosti , primijenjuje križanje, pri čemu nastaju dvije nove jedinke djece. U protivnom nastaju dva nova potomka koji su kopije roditelja. Vrijednost se najčešće kreće u intervalu , a naziva se učestalost križanja (crossover rate) [1].

U ovom su odjeljku opisani često korišteni operatori rekombinacije, klasificirani prema prikazu rješenja. Većina njih će biti opisana za slučaj kad dva roditelja generiraju dvoje djece, no većinu njih je moguće poopćiti na više roditelja ili djece. Bitno je napomenuti da za sve navedene operatore postoji implementacija čija je vremenska složenost , gdje je duljina prikaza (veličina vektora ili duljina permutacije), dok je prostorna složenost ili , ovisno o operatoru.

Križanje u jednoj točki. Najjednostavniji operator rekombinacije za bitovni prikaz rješenja je križanje u jednoj točki (one-point crossover). On radi tako da se za bitovni niz duljine slučajnim odabirom izabere cijeli broj iz intervala i potom od tog mjesta nadalje zamijene sve alele roditelja. Slika 2.3. prikazuje primjer križanja u jednoj točki.

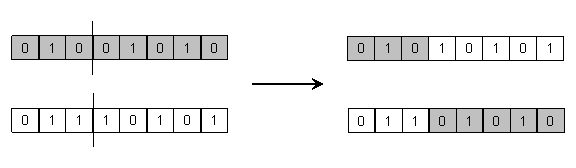
Slika 2.3. Križanje u jednoj točki

Križanje u n točaka. Križanje u jednoj točki moguće je generalizirati u križanje u točaka (n-point crossover), kod kojeg se bitovni niz dijeli na više podnizova, a djeca nastaju tako da se alterniraju podnizovi oba roditelja. Slika 2.4. ovo ilustrira za slučaj .

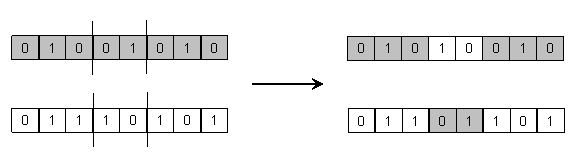
Slika 2.4. Križanje u n točaka

Jednoliko križanje. Jednoliko križanje (uniform crossover) se razlikuje od prethodna dva operatora po tome što ne dijeli bitovne nizove roditelje na podnizove, nego dodjeljuje djeci svaki bit roditelja nezavisno od ostalih, na način da za svaki bit izabere slučajnu vrijednost iz intervala , te ako je ona manja od neke unaprijed definirane vrijednosti (najčešće ), prvo dijete taj bit nasljeđuje od prvog roditelja, a inače od drugog. Drugo dijete uvijek dobiva suprotni bit od prvoga. Interesantno, u [9] se ovaj operator naziva Bernoullijevo križanje (Bernoulli crossover).

Za cjelobrojne prikaze kod kojih svaka alela može poprimiti veći broj vrijednosti, uobičajeno je koristiti iste operatore kao i kod bitovnih prikaza. Neki autori tvrde da stapanje vrijednosti (npr. aritmetička sredina) alela nema smisla za cjelobrojne prikaze, budući da to dovodi do necjelobrojnih rezultata [1].

Diskretna rekombinacija. Kod realnih prikaza moguće je koristiti sve operatore rekombinacije kao i kod bitovnih prikaza, i u tom se slučaju govori o diskretnoj rekombinaciji (discrete recombination). Ovo ima nezgodnu posljedicu da isključivo mutacija u pretraživanje unosi nove vrijednosti pojedinih gena. S druge strane, moguće je koristiti operatore koji stvaraju novu vrijednost za svaku alelu na temelju vrijednosti istih alela kod roditelja. Na taj način, u pretraživanje se unosi novi genetski materijal, no nepodobna je posljedica ta da se raspon vrijednosti alela u populaciji postepeno smanjuje. Ovaj način rekombinacije naziva se aritmetička rekombinacija (arithmetic recombination).

Jednostavna aritmetička rekombinacija. Jednostavna aritmetička rekombinacija (simple arithmetic recombination) izabire položaj rekombinacije . Potom prvih vrijednosti alela prvom djetetu dodijeljuje od prvog roditelja, a ostale računa kao aritmetičku sredinu pripadnih alela oba roditelja. Ovo je prikazano u jednadžbi (2.1), gdje vrijednosti i označavaju vrijednosti alela prvog i drugog roditelja, a je konstanta iz intervala . Drugo dijete nastaje na isti način, uz zamijenjene uloge i .

(2.1)

Jednostruka aritmetička rekombinacija. Jednostruka aritmetička rekombinacija (single arithmetic recombination) također izabire položaj , te obavlja aritmetičku rekombinaciju samo na tom mjestu. Vrijednosti ostalih alela se nasljeđuju od jednog od roditelja. Ovo prikazuje jednadžba (2.2). Drugo dijete opet nastaje uz zamijenjene uloge i .

(2.2)

Potpuna aritmetička rekombinacija. Potpuna aritmetička rekombinacija (whole arithmetic recombination) vrijednost za svaku od alela stvara aritmetičkom kombinacijom alela oba roditelja (jednadžba (2.3)).

(2.3)

Operatori rekombinacije za permutacijske probleme na prvi su pogled nešto složeniji, s obzirom na činjenicu da je potrebno sačuvati svojstvo permutacije da se svaki element pojavljuje točno jednom. Postoji cijeli niz operatora čiji je cilj očuvanje informacije od oba roditelja.

Djelomično mapirano križanje. Djelomično mapirano križanje (partially mapped crossover) je operator koji se koristi za permutacijske probleme kod kojih je bitno susjedstvo elemenata. Ovaj operator radi na sljedeći način:

1. Uzmi dva roditelja i nasumično odaberi dvije točke za križanje, te preslikaj elemente između njih iz prvog roditelja na ista mjesta kod djeteta.

2. Počevši od prve točke križanja, iz drugog roditelja izdvoji sve one elemente između točaka križanja koji još nisu preslikani.

3. Za svaki nepreslikani element nađi kod djeteta pripadni element koji je preslikan iz prvog roditelja na njegovo mjesto.

4. Ako je mjesto koje element zauzima u drugom roditelju kod djeteta slobodno, element preslikaj na to mjesto.

5. U protivnom, ako je navedeno mjesto u djetetu zauzeto elementom , element preslikaj na mjesto koje element zauzima kod drugog roditelja, ako je ono slobodno. Inače postupak ponavljaj dok ne nađeš slobodno mjesto.

6. Elemente koji nisu iz segmenta između točaka križanja potom preslikaj iz drugog roditelja u dijete. Drugo dijete se dobiva na analogan način, uz zamijenjene uloga roditelja.

Slika 2.5. ilustrira navedeni postupak – s desne strane je prikazano dijete nakon prvog, petog i šestog koraka.

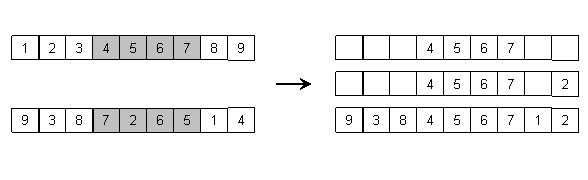
Slika 2.5. Djelomično mapirano križanje

Rubno križanje. Rubno križanje (edge crossover) je još jedan operator za probleme kod kojih je bitno susjedstvo elemenata. Informaciju o susjedstvu elemenata kod roditelja, kao što ćemo vidjeti, iskorištava u većoj mjeri nego djelomično mapirano križanje. On radi na sljedeći način:

1. Izgradi tablicu rubova – tablicu u kojoj su uz svaki element permutacije navedeni njegovi susjedni elementi u oba roditelja. Susjed prvog elementa je pritom i zadnji element permutacije. Dodatno, ako je neki element susjed drugom elementu u oba roditelja, to se evidentira u tablici.

2. Izaberi nasumično jedan od elemenata i stavi ga u potomka. Neka je on trenutni element.

3. Obriši iz tablice sva pojavljivanja trenutnog elementa.

4. Nađi sljedeći element iz liste, dajući najviši prioritet onom elementu koji je susjedan trenutnom elementu u oba roditelja, a nešto manji prioritet elementu koji ima kraću listu susjednih elemenata. Između elemenata s istim prioritetom odluči nasumično.

5. Ako je lista susjedstva prazna, probaj nastaviti postupak sa suprotne strane potomka. Ako ni to ne uspije, nasumično izaberi neki još neiskorišteni element, i nastavi od koraka 3.

Složenost ovog operatora je veća u odnosu na sve prethodne operatore, no to je cijena koju treba platiti u svrhu očuvanja informacije o susjedstvu.

Križanje u poretku. Križanje u poretku (order crossover) koristi se kod problema kod kojih je informacija o jedinki sadržana u poretku elemenata permutacije. Ovaj je operator osmišljen tako da očuva dio poretka iz jednog roditelja i relativni poredak iz drugog roditelja, a radi na sljedeći način:

1. Izaberi nasumično dvije točke križanja, i elemente između njih preslikaj iz prvog roditelja u dijete.

2. Počevši od druge točke križanja, preslikaj redom sve još nepreslikane elemente iz drugog roditelja u dijete, nastavljajući s kraja na početak niza.

3. Drugo dijete stvori na isti način, uz zamijenjene uloge roditelja.

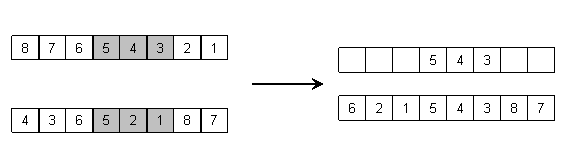
Slika 2.6. Križanje u poretku

Kružno križanje. Naposljetku, kružno križanje (cycle crossover) je operator koji kod djece nastoji sačuvati koliko je god moguće više informacija o apsolutnom poretku elemenata kod roditelja. Kod ovog se operatora elementi permutacije svrstavaju u cikluse (cycles). Ciklus je podskup elemenata permutacije koji ima svojstvo da se svaki njegov element nalazi u podskupu elemenata dobivenom izdvajanjem elemenata na istim mjestima kod drugog roditelja. Slika 2.7. prikazuje nalaženje dvaju ciklusa u nekom paru roditelja.

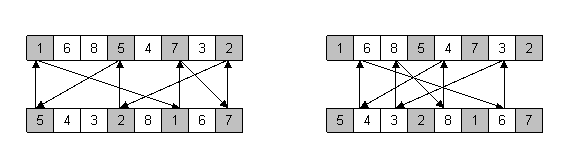
Slika 2.7. Kružno križanje – nalaženje ciklusa

Nalaženje ciklusa je jednostavno i moguće ga je opisati u pet koraka:

1. Izaberi prvo neiskorišteno mjesto i alelu prvog roditelja.

2. Pogledaj alelu na istom mjestu kod drugog roditelja.

3. Pronađi mjesto alele iz prethodnog koraka kod prvog roditelja.

4. Dodaj alelu iz prethodnog koraka u ciklus

5. Ponavljaj korake 2., 3. i 4. sve dok ne dođeš na alelu izabranu još u 1. koraku.

Navedeni postupak treba ponavljati dok god postoje alele koje nisu u nekom ciklusu. Nakon što su pronađeni svi ciklusi dvaju roditelja, djeca se stvaraju tako da svako koristi jedan ciklus od jednog roditelja, a drugi ciklus od drugog. Ako ima više od dva ciklusa, tad izbor ciklusa kod pojedinog djeteta alternira. Na ovaj je način očuvana apsolutna pozicija elemenata permutacije, kao i dio relativnog poretka.

Pohlepno križanje podobilascima. Osim ova četiri opće prihvaćena operatora križanja za permutacijske probleme, postoji još niz operatora koji se spominju u literaturi i radovima. Jedan od njih je pohlepno križanjem podobilascima (greedy subtour crossover) kojeg predlažu Sengoku i Yoshihara [29] u okviru rješavanja problema trgovačkog putnika. Ono slučajnim odabirom izabire početni element, preslikava ga na nasumični položaj u djetetu i nalazi njegov položaj u oba roditelja. Zatim preslikava jedan element prvog roditelja desno od početnog elementa ako on već nije u djetetu, i potom jedan element drugog roditelja lijevo od početnog elementa ako on već nije u djetetu. Ovaj se postupak zatim ponavlja, a kad se u nekom od roditelja naiđe na element koji je već u djetetu, iz tog se roditelja prestanu preslikavati elementi. Nakon što se to desi u oba roditelja, preostali se elementi preslikaju u dijete nasumičnim redoslijedom. Ideja iza ovog postupka je da se preslika što veće neprekinute dijelove oba roditelja u dijete. Slika 2.8. prikazuje ovaj operator na djelu – u prazni dio djeteta elementi će biti preslikani nasumično.

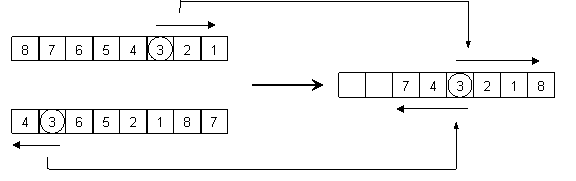
Slika 2.8. Pohlepno križanje podobilascima

Križanje u jednoj točki s djelomičnim očuvanjem. Ovaj operator navodi Ashlock u [2] kao standardni operator za permutacijske probleme. Križanje u jednoj točki s djelomičnim očuvanjem (one-point partial preservation crossover) odabire točku križanja i početnu točku u djetetu, te elemente prvog roditelja do točke križanja preslikava u dijete krenuvši od početne točke. Elemente prvog roditelja nakon točke križanja potom preslikava u dijete onim redoslijedom u kojem se pojavljuju kod drugog roditelja. Slika 2.9. prikazuje dva koraka u radu ovog operatora.

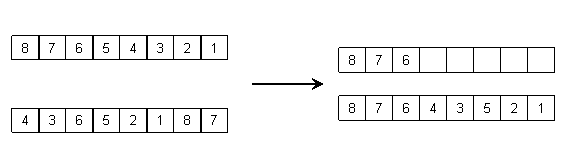
Slika 2.9. Križanje u jednoj točki s djelomičnim očuvanjem

Većinu dosad navedenih operatora moguće je poopćiti tako da koriste roditelja. Iako eksperimenti pokazuju da je to u mnogim slučajevima korisno, ne postoji teoretski dokaz da povećanje ariteta[2] operatora ima pozitivan efekt na genetski algoritam.

2.2.4. Mutacija

Mutacija je operator kod kojeg promjena parametara može imati velik utjecaj na rad genetskog algoritma. Ovaj se odjeljak fokusira isključivo na razne operatore mutacije.

Obrtanje bitova. Za binarne je prikaze uobičajeno unaprijed definirati neku vrijednost iz intervala i potom za svaki bit izvlačiti slučajnu vrijednost iz tog intervala. Ako je izvučena vrijednost manja od , vrijednost pripadnog bita se mijenja. Parametar se naziva učestalost mutacije (mutation rate). Ovakvo se križanje naziva obrtanje bitova (bit flipping).

Nasumično ponovno postavljanje. Kod kardinalnih[3] je cjelobrojnih prikaza uobičajeno korištenje operatora nasumičnog ponovnog postavljanja (random resetting), koji poput prošlog operatora za svaku alelu izvlači slučajnu vrijednost iz intervala i obavlja promjenu ako je ona manja od učestalosti mutacije, pri čemu se promjena sastoji od slučajnog odabira neke nove vrijednosti za pripadnu alelu.

Gmizajuća mutacija. Gmizajuća mutacija (creep mutation) se koristi kod ordinalnih cjelobrojnih prikaza, i ona svakoj aleli dodaje neku malu pozitivnu ili negativnu vrijednost s vjerojatnošću . Distribucija iz koje se te vrijednosti izvlače je obično simetrična oko nule i češće vraća manje vrijednosti nego veće.

Uniformna mutacija. Za prikaze realnim brojevima, koristi se jednolika mutacija (uniform mutation) kod koje se vrijednost pojedine alele s nekom fiksnom vjerojatnošću zamijenjuje slučajnom varijable iz jednolike distribucije[4] nad domenom varijable.

Neuniformna mutacija. Slično gmizajućoj mutaciji kod cjelobrojnih prikaza, kod realnih se koristi nejednolika mutacija (nonuniform mutation). Ona svakoj aleli dodaje neku vrijednost iz distribucije oko nule. Uobičajeno se koristi Gaussova distribucija, kod koje je parametar devijacije ovisan o problemu koji se rješava, no moguće je koristiti i Cauchy-evu ili neku drugu distribuciju [3].

Kod permutacija više nije moguće mijenjati svaku alelu nezavisno, pa se parametar mutacije ovdje definira kao vjerojatnost da čitava jedinka doživi mutaciju.

Mutacija zamjenom. Mutacija zamjenom (swap mutation) naprosto odabire dva mjesta u permutaciji i elemente na tim mjestima zamijeni. U [2] se ovaj operator naziva mutacija transpozicijom (transposition mutation). Slika 2.10. prikazuje primjer mutacije zamjenom kod koje su odabrani četvrti i šesti element.

Slika 2.10. Mutacija zamjenom

Mutacija ubacivanjem. Mutacija ubacivanjem (insert mutation) odabire dva elementa permutacije, te jedan od elemenata pomiče duž permutacije tako da oni budu susjedni. Slika 2.11. ilustrira jedan primjer mutacije ubacivanjem.

Slika 2.11. Mutacija ubacivanjem

Mutacija premetanjem. Mutacija premetanjem (scramble mutation) nasumično odabire podniz elemenata permutacije i potom elemente podniza nasumično pomiješa. Slika 2.12. prikazuje rad ovog operatora.

Slika 2.12. Mutacija premetanjem

Mutacija obrtanjem. Naposljetku, mutacija obrtanjem (inversion mutation) nasumično odabire dva mjesta u permutaciji i okreće redoslijed elemenata između ta dva mjesta. Na ovaj je način sačuvana informacija o susjedstvu elemenata, pa je za probleme kod kojih je bitno susjedstvo ovo jedna od najmanjih mogućih promjena koje je moguće napraviti. Slika 2.13. prikazuje operator mutacije obrtanjem na djelu.

Slika 2.13. Mutacija obrtanjem

Osim ova četiri klasična operatora mutacije opisana u [1], postoji još niz operatora mutacije i stalno nastaju novi. Opisani su još neki od njih koji su korišteni kasnije u ovom radu.

Mutacija posmakom. Jedina nama poznata primjena posmaka u genetskim operatorima spominje se kod prikaza rješenja znakovnim nizovima u [30]. Nismo našli primjenu posmaka kod permutacijskih problema u literaturi, međutim, ova se mutacija pokazala djelotvornom. Mutacija posmakom (shift mutation) je svojim djelovanjem najsličnija mutaciji ubacivanjem s razlikom da umjesto pomicanja jednog elementa po permutaciji ona odabire čitav niz elemenata i pomiče ga po permutaciji za nasumični broj mjesta. Slika 2.14. prikazuje primjer rada ovog operatora. Značaj ovog operatora bit će objašnjen u kasnijim poglavljima.

Slika 2.14. Mutacija posmakom

Mutacija zamjenom segmenata. Ovaj operator radi slično kao i mutacija zamjenom. Razlika je u tome što umjesto zamjene dvaju elemenata, mutacija zamjenom segmenata (swap segment mutation) odabire dva podniza u permutaciji i zamjenjuje im položaje. Pokazuje se korisnom za probleme u kojima je informacija sačuvana u susjedstvu elemenata – primjer za to je problem trgovačkog putnika. Slika 2.15. prikazuje rad ovog operatora.

Slika 2.15. Mutacija zamjenom segmenata

Mutacija višestrukim posmakom. Mutacija višestrukim posmakom (multishift mutation) naprosto dva puta izvodi mutaciju posmakom. Ovaj je operator korišten u eksperimentalne svrhe i o njemu će biti više riječi u kasnijim poglavljima.

Mutacija dvostrukim obrtanjem. Ovaj se operator zasniva na mutaciji obrtanjem opisanoj ranije. Umjesto da okrene redoslijed jednom podnizu permutacije, mutacija dvostrukim obrtanjem (2-inversion mutation) odabire dva susjedna podniza i okreće im redoslijede. Slika 2.16. prikazuje jednu primjenu ovog operatora.

Slika 2.16. Mutacija dvostrukim obrtanjem

2.2.5. Odabir roditelja

Postoji mnogo načina za odabir roditelja. Ono što je pri odabiru roditelja bitno je izbjeći isključivo odabir najboljih jedinki – mora postojati mogućnost da se odaberu i one lošije, inače u populaciji dolazi do preuranjene konvergencije. Drugi bitni zahtjev za odabir roditelja je neosjetljivost na pomak vrijednosti funkcije prikladnosti jedinki.

Odabir proporcionalan prikladnosti. Često korišten operator odabira roditelja je odabir proporcionalan prikladnosti (fitness proportional selection). Ovaj operator svakoj jedinki pridružuje vjerojatnost odabira prema formuli (2.4), gdje je prikladnost jedinke , ukupan broj jedinki je , a vjerojatnost odabira jedinke .

(2.4)

Na ovaj se način najprije stvara distribucija vjerojatnosti odabira pojedine jedinke za ulogu roditelja, nakon čega se prema njoj slučajno odabire određeni broj roditelja. Iz formule se jasno vide dvije činjenice. Prvo, ako je neka jedinka bolja, tad će vjerojatnost odabira te jedinke za ulogu roditelja biti veća. Drugo, suma svih vjerojatnosti odabira jedinki jednaka je 1.

Ovaj operator ima niz nedostataka. Najprije, on ima svojstvo da jedinke koje su bolje od ostalih preuzmu populaciju vrlo brzo, što često vodi do pojave već spomenute preuranjene konvergencije. Nadalje, u slučaju da su sve jedinke po vrijednosti funkcije prikladnosti vrlo blizu, distribucija vjerojatnosti će biti gotovo uniformna, što dovodi do propadanja mehanizma selekcije koji bi trebao davati značajnu prednost kvalitetnijim jedinkama (kaže se da više nema selekcijskog pritiska). Drugim riječima, operator nije irelevantan na skaliranje funkcije prikladnosti. Naposljetku, ovaj operator daje različite distribucije vjerojatnosti za translatirane vrijednosti iste funkcije – operator nije irelevantan na translaciju funkcije prikladnosti.

Da bi se riješili ovi problemi, koristi se Goldbergovo sigma skaliranje (sigma scaling), koje u izračun distribucije vjerojatnosti uzima u obzir srednju vrijednost funkcije prikladnosti populacije i standardnu devijaciju prikladnosti populacije . Prije primjene formule (2.4) za svaku se jedinku nalazi normirana vrijednost funkcije prikladnosti prema formuli (2.5).

(2.5)

Odabir odsijecanjem. Odabir odsijecanjem (truncation selection) je nešto jednostavniji. Ono odabire najboljih jedinki i slučajnim odabirom obavlja križanje kako bi se dobile nove jedinke. Spominje se u [27].

Odabir rangiranjem. Odabir rangiranjem (ranking selection) je operator koji nastoji riješiti probleme odabira proporcionalnog prikladnosti na način da jedinkama prema prikladnosti dodjeljuje rangove iz kojih se izračunavaju vjerojatnosti odabira. Pritom, veći se rang dodjeljuje boljoj jedinki. Ova diskretizacija rješava problem ovisnosti distribucije o rasponu vrijednosti funkcije prikladnosti – koliko su god jedinke po prikladnosti zbijene ili raspršene, za određivanje ranga je bitan samo njihov relativan poredak, a za određivanje vjerojatnosti odabira je bitan samo njihov rang.

Određivanje ranga je samo po sebi jasno – ono što treba razjasniti je određivanje vjerojatnosti na temelju ranga. Postoji više shema rangiranja (ranking scheme), a najčešće se koriste linearno rangiranje, za koje je dodjela vjerojatnosti opisana formulom (2.6), i eksponencijalno rangiranje, opisano formulom (2.7). Pritom je veličina populacije, označava rang, kod linearnog rangiranja je konstanta iz intervala , a se kod eksponencijalnog rangiranja odabire tako da je suma svih vjerojatnosti jednaka jedan.

	(2.6)
	(2.7)

Prethodna dva operatora na temelju izgrađene distribucije vjerojatnosti nasumično izabiru roditelje. Idealno bi bilo za svaku od jedinki uzeti onoliko preslika koliki je postotak vjerojatnosti odabira te jedinke pomnožen s veličinom populacije, međutim, kako jedinki ima konačno, nije moguće dobiti cijeli broj preslika svih roditelja. Da bi se riješio ovaj problem, koriste se razni algoritmi odabira jedinki prema distribuciji vjerojatnosti, od kojih je najjednostavniji algoritam kotača ruleta (roulette wheel algorithm). Njegov je rad moguće predočiti vrtnjom kotača ruleta kod kojeg su veličine segmenata u koje može pasti kuglica proporcionalne pripadnim vjerojatnostima. Najprije se izračuna niz vrijednosti kod kojeg je . Potom se izvlače nasumične vrijednosti iz uniformne distribucije nad intervalom . Za svaku od nasumičnih vrijednosti se u nizu potraži najmanji redni broj za koji je veći od nje, te se pripadna jedinka pohrani u skup roditelja (mating pool). Ako se odabire roditelja, izvlači se nasumičnih vrijednosti.

Zato što ovaj algoritam ne oslikava dobro distribuciju vjerojatnosti kad se odabire više od jedne jedinke, češće se koristi stohastičko univerzalno uzorkovanje (stochastic universal sampling), kod kojeg se umjesto izvlačenja nasumične vrijednosti, nasumična vrijednost izvlači samo jednom iz intervala , te se na temelju nje računa ostalih vrijednosti na način da se početno izvučenoj vrijednosti dodaje . Ovo se može predočiti kotačem ruleta koji ima jednako razmaknutih ruku.

Turnirski odabir. Naposljetku, napomenimo da nije uvijek moguće graditi distribuciju vjerojatnosti na temelju čitave populacije, jer populacije mogu biti jako velike, ili podijeljene na više računalnih sustava. Ponekad ne postoji univerzalna definicija funkcije prikladnosti, već se prikladnost određuje usporedbom više jedinki – primjer za to je optimizacija neuronske mreže koja igra neku igru na ploči poput dame, ili stroj s konačnim brojem stanja koji sudjeluje u iterativnoj zatvorenikovoj dilemi (vidi [2]). U tim se slučajevima često koristi turnirski odabir (tournament selection), operator koji ima korisno svojstvo da ne zahtjeva znanje o čitavoj populaciji, već samo relaciju rangiranja bilo kojeg para jedinki. On radi tako da slučajno odabere neki skup od jedinki, gdje se naziva veličina turnira (tournament size), i izabire najbolja jedinka među njima, te taj postupak ponavlja sve dok ne sakupi željeni broj roditelja. Parametar izravno utječe na selekcijski pritisak – što je turnir veći, veća je i vjerojatnost da će se u njemu pojaviti iznadprosječne jedinke, te da će iste biti i odabrane.

Turnirski je odabir moguće implementirati i da radi stohastički – da odabranom podskupu jedinki odredi vjerojatnosti na temelju prikladnosti i potom najbolju jedinku u tom podskupu odabere na temelju distribucije vjerojatnosti poput ranije opisanih operatora.

Jedan oblik selekcije je i gladijatorska turnirska selekcija (gladiatorial tournament selection) koju opisuje Daniel Ashlock u [2]. Kod nje se iz populacije odabiru nasumično dva para jedinki te se evaluiraju jedno u odnosu na drugo u parovima. Lošiji par jedinki se iz populacije odbacuje, dok se iz boljih križanjem dobivaju dvije nove jedinke koje postaju dio populacije. Round robin tournament selection je selekcija kod koje se međusobno evaluiraju svi mogući parovi jedinki populacije. Postoji još dosta inačica turnirske selekcije i ovdje su navedene samo neke.

2.2.6. Odabir preživjelih

U ovom je odjeljku opisano nekoliko bitnih strategija odabira jedinki za sljedeću generaciju genetskog algoritma. Odabir preživjelih jedinki se često naziva i zamjena (replacement), te ta dva pojma smatraju istoznačnima. Za zamjenu je moguće koristiti većinu operatora navedenih u prošlom odjeljku.

Dobna zamjena (age-based replacement) podrazumijeva da se pri odabiru preživjelih jedinki u obzir ne uzima njihova prikladnost, već broj generacija koje su preživjela. Nakon što je jedinka proživjela neki broj generacija, naprosto se miče iz populacije.

Zamjena prema prikladnosti (fitness-based replacement) je prilično širok pojam, s obzirom da postoji mnogo strategija za odabir jedinki za sljedeću generaciju iz skupa od roditelja i potomaka. Sve strategije za odabir roditelja spadaju u ovu kategoriju. Od načina odabira koji nisu spomenuti u prošlom odjeljku, istaknimo strategiju zamjene najgorih (replace worst) koja iz populacije miče najgorih jedinki. Kako ona gotovo uvijek vodi do preuranjene konvergencije, koristi se isključivo uz velike populacije ili politiku kod koje nema duplikata u populaciji. Spomenimo također elitizam (elitism), strategiju koja se koristi u tandemu s bilo kojom već opisanom strategijom. Ona uvijek prati najbolju (ili nekoliko najboljih) jedinku u populaciji, te se brine da ta jedinka, između ostalih odabranih nekom drugom strategijom, svakako bude odabrana za sljedeću generaciju. Na ovaj se način osigurava da najbolja dosad nađena jedinka u svakom trenutku bude očuvana.

Umjesto selekcije, svi operatori navedeni u ovom i prošlom odjeljku mogu funkcionirati na principu eliminacije. Umjesto da se nekim od navedenih postupaka odabiru jedinke za sljedeću generaciju (pri čemu se ista jedinka u novoj populaciji može naći i više puta), istim se postupcima eliminiraju jedinke iz trenutne populacije (pri čemu se ista jedinka u novoj populaciji može naći najviše jednom). Odluka o korištenju eliminacije ili selekcije može imati utjecaj na brzinu konvergencije algoritma – eliminacija može usporiti konvergenciju, pa čak i spriječiti preuranjenu konvergenciju (iako ovo ovisi o dosta faktora).

3. Upravljanje parametrima genetskog algoritma

Dosada je naveden niz primjera različitih sastavnica genetskog algoritma, te je pokazano da se uz pojedine sastavnice vežu određeni parametri. Tipičan primjer za to je vjerojatnost kod mutacije, odnosno vjerojatnost kod križanja. Za vrijednosti ovih parametara često se uzimaju neke unaprijed određeni ili preporučeni iznosi, no općenito su vrijednosti tih parametara usko vezane uz problem koji genetski algoritam rješava. Pronalaženje optimalnih vrijednosti parametara genetskog algoritma za dani problem često je samo po sebi jednako složen (i složeniji) problem kao i problem koji bi genetski algoritam trebao riješiti, s obzirom da se svi slobodni parametri genetskog algoritma mogu staviti u jedan vektor koji se potom optimira prema broju generacija koje su potrebne genetskom algoritmu da nađe rješenje.

Postupak nalaženja optimalnih vrijednosti parametara genetskog algoritma naziva se podešavanje parametara (parameter tuning). Osim što ovo može biti složen postupak, kao što je već navedeno, treba napomenuti da postoje teoremi koji dokazuju nepostojanje optimalnih parametara genetskog algoritma za sve probleme[5]. Nadalje, rad genetskog algoritma je dinamičan proces, u smislu da su u različitim koracima pretrage pogodne različite vrijednosti parametara. Npr. veća vrijednost za neuniformnu mutaciju korisna je na početku rada algoritma kako bi se na početku pretražilo što veće područje. Kasnije, kad je već pronađeno područje optimuma, pogodno je smanjiti vrijednost kako bi se suboptimalne jedinke grupirane oko optimuma istome lakše pridružila.

Postupak promjene vrijednosti parametara tijekom rada genetskog algoritma naziva se upravljanje parametrima (parameter control). Zadatak je ovog poglavlja klasificirati tehnike upravljanja parametrima i pokazati neke od metoda za to (Slika 3.1.).

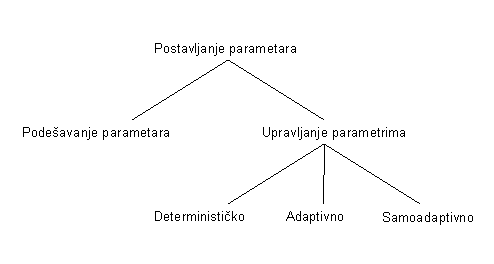
Slika 3.1. Taksonomija postavljanja parametara

3.1. Upravljanje parametrima

Kada se govori o upravljanju parametrima, treba napomenuti da postoji više podjela tehnika upravljanja parametrima – oslanjamo se na podjelu koju predlažu Eiben i Smith [1], koja se temelji na sljedećim kriterijima:

Što se mijenja? (evaluacijska funkcija, rekombinacija, mutacija, selekcija, veličina i oblik populacije)
Na koji se način mijenjaju vrijednosti parametara? (deterministički, adaptivno ili samoadaptivno)
Na temelju čega se mijenjaju vrijednosti parametara? (npr. raznolikost populacije, broj poboljšanja u zadnjih N generacija, broj proteklih generacija…)
Koji je opseg promjene? (na razini populacije, pojedinca ili kromosoma)

Sljedeći su odjeljci organizirani prema prvom kriteriju, a unutar njih je napravljena podjela prema drugom kriteriju, koji zahtijeva objašnjenje.

Naime, determinističko upravljanje parametrima označava promjenu vrijednosti parametara prema nekom unaprijed određenom pravilu. Primjerice, vjerojatnost mutacije može padati do nule linearno s brojem proteklih generacija. Tipično se ovakvo upravljanje oslanja na broj proteklih generacija. Važno je primijetiti da determinističko upravljanje nema povratnu vezu sa stanjem pretrage. U danom primjeru, vjerojatnost mutacije ne ovisi ni o najboljoj jedinki u populaciji, ni o raspršenosti jedinki, već isključivo o broju proteklih generacija.

Za razliku od determinističkog, adaptivno upravljanje parametrima je ono kod kojeg postoji povratna veza između stanja pretrage i smjera i veličine promjene vrijednosti parametra. Npr. povećanje vjerojatnosti mutacije ako nakon N generacija nije bilo poboljšanja jedinki je primjer adaptivnog upravljanja, jer se za promjenu vrijednosti vjerojatnosti mutacije koristi informacija o pretrazi. Pritom mehanizam promjene vjerojatnosti mutacije nije dio prije opisanog genetskog algoritma, već predstavlja njegovu dodatnu sastavnicu.

Naposljetku, samoadaptivno upravljanje je ono kod kojeg mehanizam genetskog algoritma obavlja upravljanje parametrima. Parametri koji se koriste za pojedine sastavnice genetskog algoritma ugrađeni su u pojedine jedinke kao dodatni kromosomi. Ovaj se tip upravljanja zasniva na premisi da bolje vrijednosti parametara dovode do optimalnijih jedinki, pa se te iste bolje vrijednosti parametara s većim uspjehom propagiraju kroz populaciju. Samim time, za propagaciju boljih vrijednosti odgovoran je mehanizam genetskog algoritma.

U nastavku je dan niz primjera upravljanja parametrima za svaku od sastavnica genetskog algoritma, s obzirom na način promjene vrijednosti parametara.

3.2. Evaluacijska funkcija

Evaluacijske se funkcije tipično ne mijenjaju u evolucijskim algoritmima, jer se one smatraju dijelom problema. Postoji mnogo primjera gdje je evaluacijska funkcija intuitivna i proizlazi iz problema. Jedan takav slučaj je optimizacija funkcije, gdje je evaluacijska funkcija upravo ona funkcija čiji se optimum traži.

No, često evaluacijska funkcija nije poznata, kao što je slučaj u ocjeni nekog igrača igre na ploči. Navedimo kao primjer evaluaciju neuronske mreže koja daje ocjenu pojedinog stanja ploče u igri dame [5]. U sukobu dvojice igrača nije moguće dati objektivnu ocjenu nečije igre – na raspolaganju je jedino informacija o tome je li pobijedio, izgubio ili je igra završila izjednačeno. U tom smislu, jedino što je moguće je ocijeniti pojedinog igrača u odnosu na ostale igrače koji su trenutno u populaciji, na način da svaki igrač odigra protiv svakog drugog ili nekih drugih, te se potom svakom igraču na temelju ishoda igara koje je odigrao dodijeli normirana ocjena. Ovo nalikuje na turnirsku selekciju, gdje je evaluacijska funkcija s njom usko povezana.

Diskutabilno je da li se ovdje radi o upravljanju parametrima i o adaptivnoj evaluacijskoj funkciji, s obzirom da se nigdje doslovce ne mijenjaju parametri, no ovaj pristup ovdje navodimo kao primjer adaptivne evaluacijske funkcije budući da postoji povratna veza između trenutnog stanja pretrage (trenutno raspoloživih jedinki, odnosno igrača, u populaciji) i evaluacijske funkcije. Da se svaka od jedinki evaluirala sukobom s nekim vanjskim agentom čija se djelotvornost ne mijenja kroz generacije algoritma (npr. ljudskim igračem, ili računalnim igračem koji je izgrađen nekom drugom metodom), tad ne bi bilo povratne veze sa stanjem pretrage.

Drugi se primjer upravljanja parametrima evaluacijske funkcije često spominje u okviru problema zadovoljenja ograničenja (constraint satisfaction problems) i optimizacijskih problema s ograničenjima (constraint optimization problems). Kod prvih je nužno naći rješenje koje zadovoljava neki niz uvjeta, a kod drugih je nužno naći isto takvo rješenje, koje je k tomu još i optimalno s obzirom na neku ciljnu funkciju (objective function) [6]. Jedan primjer optimizacijskog problema s ograničenjima je nalaženje optimuma funkcije uz niz ograničenja u obliku jednadžbi i nejednadžbi. Očito je da ovdje ciljna funkcija ne može igrati ulogu evaluacijske, kao što je to slučaj kod optimizacijskih problema. Općenito, iz tog se niza ograničenja gradi neka funkcija kazne (penalty function), koja daje vrijednost kazne u skladu s mjerom u kojoj se ograničenja krše – ako je, na primjer, rješenje ograničeno na neki interval, tad funkcija kazne vraća 0 za jedinke unutar tog intervala, a udaljenost jedinke do intervala u slučaju da je jedinka izvan intervala. Na temelju ciljne funkcije i funkcije kazne se onda gradi evaluacijska funkcija na način kao što je to prikazano u jednadžbi (3.1), gdje je evaluacijska funkcija, ciljna funkcija, parametar je neki realni broj, a funkcija kazne.

(3.1)

Funkcija gradi se od primitiva koji vraćaju veću pozitivnu vrijednost ako je kršenje ograničenja veće. Načina na koji se dobiva od skupa primitiva ima više, no jedan jednostavan primjer je suma svih primitiva. Primitivi ovise o prirodi problema koji se rješava. Uzmimo za primjer optimizaciju realne funkcije s ograničenjima. Jednadžbe koje rješenje treba zadovoljiti i nejednadžbe koje rješenje treba zadovoljiti mogu se zapisati u normaliziranom obliku prikazanom u jednadžbama (3.2).

(3.2)

U skladu s tim, moguće je pojedine primitive definirati kao u jednadžbi (3.3).

(3.3)

Parametar u jednadžbi (3.1) je najčešće adaptivan, te ga je moguće mijenjati tijekom rada genetskog algoritma na više načina.

Determinističko upravljanje parametrom proučeno je u radu Joinesa i Houcka [7]. Parametar se u svakoj generaciji računa prema formuli (3.4), gdje su i konstantne vrijednosti određene prije početka rada algoritma, a je redni broj generacije.

(3.4)

Očito je iz formule (3.4) da parametar raste s brojem proteklih generacija doprinoseći sve većoj važnosti funkcije kazne, tj. ograničenja. Na ovaj je način na početku pretrage pretraživati više jedinke koja krše ograničenja, jer je pretpostavka da takve jedinke mogu kasnije doprinijeti nalaženju optimuma koji zadovoljava ograničenja. Slika 3.2. ilustrira jedan primjer ciljne funkcije kod koje bi to mogli biti tako – postoji velika vjerojatnost da se jedinke grupiraju kod gornje granice intervala ako se ograničenja odmah uzmu u obzir. Druga interpretacija je da ovakvo upravljanje parametrima u početku pretrage nalazi optimalne jedinke s manjim osvrtom na ograničenja, i te iste optimalne jedinke kasnije služe kao referentne točke za nastavak pretrage kako funkcija kazne dobiva sve veću težinu – lakše je najprije naći optimum, pa tek onda tražiti optimum u skladu s ograničenjima. Treba napomenuti da ova metoda uvodi dva nova parametra koje je potrebno podesiti prije pokretanja genetskog algoritma. Dodatno, Joines i Houck su funkciju kazne formirali ne na temelju sume svih primitiva ograničenja, već na temelju sume njihovih -tih potencija, što uvodi još i treći parametar.

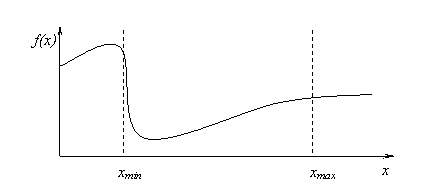
Slika 3.2. Primjer krajolika funkcije uz ograničenja

Sličan primjer determinističkog upravljanja evaluacijskom funkcijom opisuju Michalewicz i Attia [8]. Algoritam Genocop II, koji je u biti izgrađen na temelju genetskog algoritma koji poziva više puta, tijekom svake iteracije[6] koristi jednu vrijednost za parametar , prema formuli (3.5), gdje je konstanta nazvana temperaturom[7]. Na kraju svake iteracije se temperatura smanjuje prema nekoj formuli koja ovisi o rednom broju iteracije.

(3.5)

Algoritam Genocop II na kraju svake iteracije odabire najbolju jedinku iz čitave populacije, te od njenih preslika oblikuje inicijalnu populaciju za sljedeći poziv genetskog algoritma. Smanjivši temperaturu , ponovo se poziva genetski algoritam, te se to ponavlja sve dok temperatura ne dosegne konačnu vrijednost . Pritom treba primijetiti da ova metoda zahtjeva da se unaprijed podese parametri (početna temperatura) i .

Primjer adaptivnog upravljanja parametrom opisali su Bean i Hadj-Alouane [9]. Oni na kraju svake generacije podešavaju parametar prema formuli (3.6). Pritom, označava skup svih prihvatljivih (feasible) rješenja, tj. svih onih rješenja koja za zadani problem ne krše ograničenja, a označava najbolju jedinku -toj generaciji. Konstante i biraju se tako da budu različite kako bi se spriječilo ponavljanje istih vrijednosti (cycling). Redni broj trenutne generacije označen je s .

(3.6)

Ideja formule (3.6) je da se težina funkcije kazne smanji u slučaju da je u zadnjih generacija najbolja jedinka u populaciji zadovoljavala ograničenja. U suprotnom slučaju, ako je najbolje jedinka u populaciji u zadnjih generacija kršila ograničenja, tad težinu kazne treba povećati, kako bi se dala prednost onim jedinkama koja imaju lošiju[8] vrijednost ciljne funkcije, ali su prihvatljiva.

U ovom se postupku jasno nazire ranije spomenuta povratna veza. Dok je kod determinističkog upravljanja na prirodu evaluacijske funkcije utjecao isključivo redni broj generacije, oblikom evaluacijske funkcije u ovom slučaju upravlja stanje pretrage (u ovom slučaju osobine najboljih dosad nađenih jedinki). To znači da ne postoji unaprijed određen obrazac njene promjene, već njena brzina i smjer njene promjene ovise o problemu.

Još jedan primjer adaptivnog upravljanja evaluacijskom funkcijom opisuju Eiben i van der Hauw [10]. Tu se umjesto parametra kojim se množi funkcija kazne koristi vektor težina koji svaki od elemenata funkcije kazne množi nekim drugim koeficijentom, vidi (3.7). Ovo zahtjeva promjenu definicije funkcije kazne – ona više ne vraća realnu vrijednost, nego vektor dimenzije jednake broju ograničenja, koji se kao i ranije gradi od skupa primitiva. Najjednostavniji način izgradnje funkcije kazne je tako da se svaka komponenta vektora koji vraća sastoji od isključivo jednog primitiva (slično kao i ranije kod sume primitiva).

(3.7)

Eiben i van der Hauw ne daju svakom od ograničenja jednaku težinu, jer smatraju da je neke od ograničenja teže zadovoljiti od drugih. Nemoguće je podešavanjem parametara za bilo kakav problem predvidjeti koje su najbolje težine za sva ograničenja, pa se ovo proširenje koristi u kombinaciji s adaptivnim upravljanjem.

Inicijalno se svim ograničenjima dodijeli neka vrijednost . Svakih evaluacija nađe se najbolje jedinka u populaciji, te se onim ograničenjima koja ta jedinka krši poveća pripadni parametar za unaprijed određeni iznos . Vrijednosti težina se na ovaj način određuju povratnom vezom.

Samo-adaptivno upravljanje nije česta pojava kod evaluacijske funkcije. Eiben, Hinterding i Michalewicz to objašnjavaju činjenicom da se dvije jedinke unutar iste populacije mogu razlikovati isključivo po vrijednosti vlastite težine funkcije kazne , što bi davalo različitu ocjenu jedinkama koja su zapravo identična [4]. Jasno je iz toga da bi ugrađivanje težine u vektor rješenja dovelo do kontra-efekta, jer bi lošije jedinke s pogodnijim iznosom parametra brzo zavladala populacijom. Kad se samo-adaptivnost koristi u sprezi s ostalim sastavnicama genetskog algoritma, kao što su to mutacija i rekombinacija, na evaluaciju pojedine jedinke nikako ne utječu komponente nastale ugradnjom parametara, što ovdje nije slučaj, jer ugradnja parametra u vektor rješenja omogućuje evoluciji da “vara” poboljšavajući isključivo taj parametar.

3.3. Rekombinacija

Već je ranije spomenuto da rekombinacija obavlja lokalno pretraživanje u prostoru rješenja uzimajući informacije o kvaliteti jedinke od roditelja, a taj se pojam naziva iskorištavanje (exploitation). Ideja kod upravljanja rekombinacijom je natjerati rekombinaciju da u stvaranju djeteta iskoristi one informacije jedinki roditelja (ili čitave populacije) koje čine tog roditelja dobrim. Sjetimo se, u prethodnom su poglavlju opisani operatori rekombinacije koji rade nasumični odabir pojedinih dijelova jedinki roditelja pazeći pritom isključivo na bliskost jedinke djeteta (naročito su detaljno u tom smislu opisani operatori za permutacijske probleme), no nijedan od njih nije u obzir uzimao davanje prednosti onom dijelu jedinke roditelja koje je utjecalo na poboljšanje kvalitete roditelja. U ovom je odjeljku opisano nekoliko modela rekombinacije koji u obzir uzimaju kvalitetu populacije, kvalitetu roditelja ili kvalitetu samo dijela roditelja.

Naglašavamo najprije da nam nije poznat primjer determinističkog upravljanja rekombinacijom. Možda ima smisla kroz niz generacija mijenjati vjerojatnost križanja prema nekom unaprijed određenom pravilu, ali takav nam eksperiment nije poznat.

Yang predlaže metodu adaptivnog križanja koje se zasniva na statističkim informacijama iz čitave populacije. Načelna je ideja da se za svaki bit rješenja[9] na temelju učestalosti pojavljivanja jedne te iste vrijednosti na mjestu tog bita kod svih rješenja u populaciji odredi vjerojatnost za uniformno križanje, te se potom provede uniformno križanje. Ako se ista vrijednost nekog bita pojavljuje češće, znači da je u populaciji ta vrijednost tog opće prihvaćena, pa je vjerojatnost zamjene bitova kod uniformnog križanja manja.

Konkretno, na kraju svake generacije za svaki se bit odredi učestalost pojavljivanja vrijednosti 1 na mjestu tog bita . Potom se određuje vjerojatnost zamjene tog bita za uniformno križanje prema formuli (3.8), gdje određuje najveću dozvoljenu vjerojatnost zamjene, a najmanju.

(3.8)

Lako je utvrditi da gornja funkcija ima oblik trokuta i da daje najmanju vjerojatnost zamjene onim bitovima čija vrijednost u populaciji prevladava, bila to vrijednost 0 ili 1. Tu se jasno vidi težnja da se ne mijenjaju oni bitovi za koje se smatra da su im vrijednosti dobre. Yang nudi i druge oblike funkcija za određivanje vjerojatnosti, te ih temeljito opisuje u [11].

Sličan oblik adaptivnog upravljanja opisuje Davis, koristeći istovremeno više različitih operatora rekombinacije s različitom učestalošću [4]. Ako se tijekom evolucije ustanovi da neki od operatora daje bolje jedinke od ostalih, učestalost korištenja tog operatora se povećava.

Eiben, Kuyper i Thijssen ideju odabira operatora prema kvaliteti jedinki koje generira koriste u tandemu s podjelom populacije na podpopulacije (subpopulations) koje koriste različite operatore križanja [12]. Korišteni operatori križanja su križanje u točaka i dijagonalno križanje (diagonal crossover). Dijagonalno križanje je operator koji uzima roditelja i odabire točaka za križanje, te stvara djece tako da -to dijete dobiva prvi segment od -tog roditelja, a svaki sljedeći od sljedećih roditelja, nastavljajući s prvim nakon zadnjeg. Slika 3.3. prikazuje nastanak tri djeteta iz tri roditelja dijagonalnim križanjem.

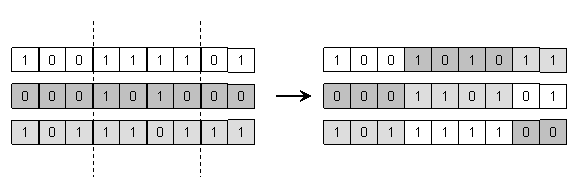
Slika 3.3. Dijagonalno križanje

Svaka od podpopulacija koristi jedan od operatora križanja, a u slučaju dijagonalnog križanja neki aritet operatora. Nakon određenog broja generacija, obavlja se izmjena jedinki između podpopulacija na način da slabije populacije moraju dati više jedinki. Ta se izmjena naziva migracija (migration). Konkretno, za svaku od podpopulacija se nađe prikladnost najlošije jedinke i prikladnost najbolje , te srednja prikladnost podpopulacije . Potom se računa vrijednost kako je to prikazano u jednadžbi (3.9).

(3.9)

Svaka od podpopulacija mora se odreći svojih nasumično odabranih jedinki, gdje je konstanta iz intervala , a veličina podpopulacije . Potom se sve tako dobivene jedinke dijele jednoliko između svih podpopulacija, a ostatak se podijeli podpopulacijama s najboljom prosječnom prikladnošću. Rezultat tog postupka je da se lošije podpopulacije moraju odreći više svojih pojedinaca, a bolje njih manje. Netko će možda primijetiti da sustav dodjele s obzirom na vrijednost nije sasvim pravedan, jer neke podpopulacije mogu imati veći raspon između najbolje i najlošije prikladnosti, što im dalje manju vrijednost , i time odricanje od manjeg broja pojedinaca, ali treba se sjetiti da ovaj mehanizam nakon određenog broja generacija nasumično izmijenjuje jedinke između podpopulacija i time ujedno osigurava da najveće i najmanje prikladnosti ostanu otprilike jednake.

Oprečni mehanizam redivizije (redivision) ponekad vraća neke od jedinki u slabije podpopulacije i time osigurava da one nikad ne nestanu potpuno, jer se smatra da njihovi operatori križanja mogu doprinijeti kasnije tijekom pretrage, ako već nisu na početku. Krajnji je rezultat da se češće primijenjuju oni operatori križanja koji daju bolje rezultate, pa je ovo još jedan primjer adaptivnog upravljanja.

Kod rekombinacije se mnogo češće koristi samo-adaptivno upravljanje. Jedan jednostavan oblik samo-adaptivnog križanja, nazvan jednobitna adaptacija (1bit adaptation), predlaže Spears [16]. Svakoj se jedinki dodaje jedan dodatni bit čija vrijednost 0 označava da će se za rekombinaciju koristiti uniformno križanje, dok vrijednost 1 označava križanje u dvije točke. Ako oba roditelja imaju istu vrijednost bita, odluka o uporabi operatora križanja je jednoznačna, u protivnom se baca novčić[10]. U dijete se ugradi vrijednost bita križanja ovisno o korištenom operatoru. Udio pojedinih vrijednosti tog bita u populaciji izravno govori o tome koliko je koji operator uspješan u stvaranju potomaka. S obzirom da će se uspješniji operator češće i koristiti, jer je prisutan u većem broju jedinki, samo-adaptivno upravljanje je ovdje očito.

Primjer kod kojeg je samo-adaptacija vidljiva na razini gena predložio je Louis [13]. Maskirano križanje (masked crossover) pretpostavlja da je bitovnom prikazu rješenja dodan niz bitova maske koji je iste dužine. Slika 3.4. prikazuje način križanja dvaju roditelja, gdje i označavaju maske roditelja.

Slika 3.4. Pseudokod maskiranog križanja

Na ovaj način nastaje tri tipa djece: dobra djeca koja su bolja od oba roditelja, osrednja djeca koja su po prikladnosti između oba roditelja i loša djeca koja su jednako dobra ili lošija od lošijeg roditelja. Postoji šest mogućih kombinacija para djece koji nastaje, i u skladu s tim postoje i pravila za preslikavanje maske s roditelja na djecu:

1. Ako su oba djeteta dobra, tad se smatra da su oba roditelja doprinijeli stvaranju dobre djece, pa se maske za djecu stvaraju tako da se obavi ILI operacija između maski roditelja, a bitovi koji ne postanu postavljeni se postavljaju bacanjem novčića.

2. Ako su oba djeteta loša, roditelje treba kazniti promjenom njihove maske. Prvom djetetu treba postaviti na 0 onaj bit maske kod kojeg pripadni bit drugog roditelja dominira nad prvim (bit drugog roditelja ima vrijednost 1, a prvog 0), a na mjesta gdje su oba roditelja dominantna, treba baciti novčić za određivanje da li će se bita maske djeteta postaviti. Prvom roditelju treba postaviti mjesta na kojima je bio dominiran ili je dominirao bacanjem novčića. Sličan se postupak obavlja za drugo dijete i drugog roditelja

3. U svim ostalim slučajevima, pojedino dijete nasljeđuje masku od roditelja.

Nakon svake rekombinacije se dodatno na masku primijenjuje operator mutacije okretanjem bitova.

Jasno je da ovakav postupak koristi samo-adaptivno upravljanje, jer se operator križanja u svakom trenutku prilagođava svakom pojedinom genu jedinke na temelju prethodnih uspjeha u traženju boljih jedinki, te mu ujedno podešava masku ovisno o ishodu rekombinacije.

Vekaria i Clack primijetili su da ovaj operator ne obraća pozornost na veličinu promjene funkcije prikladnosti kod djeteta [15], a da nakon što je bit maske postavljen, nije moguće u jedinku zapisati daljnje doprinose tog bita. U tom smislu, navodimo operator adaptivnog jednolikog križanja (adaptive uniform crossover) kojeg su predložili White i Oppacher. On, umjesto da svakom bitu rješenja pridružuje jedan bit maske, svakom bitu pridružuje jedno od stanja gdje je paran broj. Na početku se pretrage svakoj jedinki ta stanja dodijele nasumično. Veće stanje označava veću zaslugu bita za stvaranje dobrih jedinki. Pri križanju se pojedini bit djeteta određuje na temelju stanja automata – viši redni broj stanja znači da je vjerojatnost preuzimanja tog bita od tog roditelja veća. Ako na taj način nastane dijete čija je prikladnost lošija od nekog od roditelja, roditelju će se stanje za one bitova koji su od njega preuzeti morati smanjiti za jednu razinu. Suprotno, ako je dijete bolje od nekog roditelja, tada se bitovi koji su od njega preuzeti nagrađuju tako da im se pripadno stanje povisi za jednu razinu. Ovo kasnije omogućava preuzimanje bitova koji su stvorili veći broj bolje djece s većom vjerojatnošću, i obratno.

Vekaria i Clack su također ponudili operator rekombinacije, tzv. selektivno križanje (selective crossover) [14]. Umjesto da dodijele svakom od bitova rješenja dodatni bit ili niz stanja, oni pojedinom bit dodijeljuju realni broj koji nazivaju mjerom dominacije (dominance value). Iako je adaptivno jednoliko križanje imalo prednost pred maskiranim križanjem da za svaki bit važnost određuje na više različitih razina, to podešavanje nije bilo razmjerno veličini promjene funkcije prikladnosti, već je ovisilo samo o predznaku promjene. Selektivno križanje dodatno proširuje ideju pridavanja važnosti pojedinom bitu rješivši i taj problem.

Spomenimo još samo da prethodna tri operatora podrazumijevaju model stabilnog stanja (steady state model) populacije, u kojem jedinke ostaju u populaciji tijekom više od jedne generacije. S obzirom da se nakon svakog križanja podešavaju i roditelji, razlog ovome je očigledan.

Naposljetku, dajemo nešto drugačiji primjer samo-adaptivne rekombinacije koji predlažu Smith i Fogarty [17][18] je povezanošću evoluiran genetski operator (linkage evolving genetic operator), kod kojeg nije cilj iskoristiti informaciju o važnost pojedinih kromosoma, već informaciju o važnosti pojedinih blokova kromosoma. Svakom od kromosoma rješenja dodaju se još dva dodatna bita koji označavaju povezanost (linkage) sa susjedna dva kromosoma. Dva se susjedna kromosoma pritom smatraju povezanima ako su obojici postavljeni pripadni bitovi (npr. desnom kromosomu je postavljen lijevi bit, i obratno). Na taj se način više povezanih kromosoma ulančava u blokove.

Križanje povezanošću radi tako da od nekog broja jedinki stvara tzv. genetski bazen (gene pool), na način da se nasumično odabere jednu podobnu (eligible) jedinku. Podobna jedinka je ona jedinka kod kojee postoji blok kromosoma koji počinje od trenutnog slobodnog položaja u djetetu. Na početku je svaka od jedinki podobna, jer je dijete prazno. Potom se redom ispituju ostale jedinke dok se do neke mjere ne napuni genetski bazen, nakon čega se održava turnirska selekcija za odabir bloka koji će se staviti u dijete. Postupak se nastavlja gradnjom novog genetskog bazena, i ponavlja sve dok dijete ne bude napunjeno blokovima. Jednostavnom analizom je moguće pokazati da će ovaj postupak uvijek biti moguće izvesti. Također, lako je ustanoviti da ovaj postupak može dovesti do izgradnje većih blokova, što je u konkretnoj implementaciji u ravnoteži s mutacijom koja razbija blokove na manje. Slika 3.5. prikazuje rad ovog operatora.

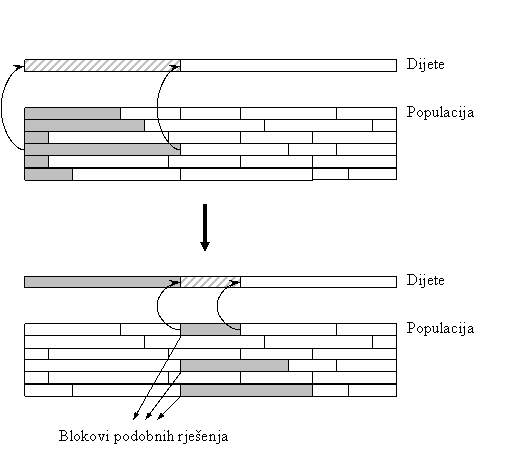
Slika 3.5. Križanje povezanošću

3.4. Mutacija

Mutacija je posebno proučavana sastavnica genetskih algoritama. Pogotovo je velik trud uložen u određivanja optimalne vrijednosti učestalosti mutacije . Niz radova upućuje da bi se učestalost mutacije trebala nalaziti u intervalu . S druge strane, Mühlenbein je izveo formulu (3.10) koja u vezu dovodi optimalnu učestalost mutacije i broj kromosoma rješenja , čiju su ispravnost eksperimentalno utvrdili Smith, Fogarty i Bäck [4].

(3.10)

Što se tiče determinističkog upravljanja učestalošću mutacije, postoji dosta radova u kojima se učestalost mutacija smanjuje prema nekom unaprijed određenom zakonu koji je najčešće u sprezi s rednim brojem generacije [19][20], za što je primjer formula (3.11) koju je eksperimentalno koristio Fogarty.

(3.11)

Kasnije su Hesser i Männer izveli teoretske izraze za optimalne vrijednosti parametra mutacije [20], što je prikazano u formuli (3.12), gdje su , i konstante koje se za jednostavne probleme mogu procijeniti, je veličina populacije, a je broj kromosoma.

(3.12)

Bäck i Schütz su također kroz generacije smanjivali učestalost mutacije prema formuli (3.13), s ciljem da je na početku učestalost mutacije , a na kraju, nakon generacija, .

(3.13)

Dosad prikazane sheme upravljanja učestalošću mutacije dovodile su ovu veličinu isključivo u ovisnost s brojem proteklih generacija. Bäck nudi izraz (3.14) koji u vezu dovodi učestalost mutacije i udaljenost neke jedinke od optimuma. Izraz u danom obliku nije sasvim točan, jer podrazumijeva neki oblik normalizacije funkcije prikladnosti.

(3.14)

Prijašnji oblici upravljanja mutacijom odnosili su se na učestalost mutacije, no moguće je mijenjati i druge parametre mutacije. Janikow i Michalewicz eksperimentirali su s neuniformnom mutacijom smanjujući kroz vrijeme raspršenost razdiobe iz koje su vukli slučajne vrijednosti. Konkretno, -ti kromosom jedinke mijenjali su prema izrazu (3.15), gdje je vrijednost kromosoma, slučajna jednobitna varijabla, i granice domene vrijednosti kromsoma, a funkcija koja vraća slučajnu vrijednost iz intervala , za koju se vjerojatnost pojave vrijednosti bliskije 0 povećava s povećanjem parametra - definicija joj je dana u (3.16), gdje je slučajna varijabla iz intervala , najveći broj generacija, a parametar koji određuje stupanj neuniformnosti.

	(3.15)
	(3.16)

Ideja ovakvog oblika upravljanja je da je na početku pretraživanja prostora rješenja potrebno proći veliki prostor, pa bi intervali u kojima se dešavaju mutacije trebali biti veći, dok je kasnije, pri kraju pretraživanja, prirodno dozvoliti blaže mutacije, s obzirom da se pretraživanje približava kraju.

Kod neuniformne mutacije se često koristi neka od već poznatih distribucija vjerojatnosti. Za većinu distribucija se vežu neki karakteristični parametri, kao što se za Gaussovu veže standardna devijacija . Parametar je moguće mijenjati kroz vrijeme iz istog razloga kao i u prethodnom primjeru. Međutim, optimalan postupak promjene tog parametra kroz vrijeme nije jedinstven za sve probleme, pa se, kao i ranije, koristi adaptivno upravljanje ovim parametrom.

Najpoznatiji primjer adaptivnog upravljanja je Rechenbergovo “pravilo petine uspješnih mutacija” (1/5 success rule), koje se zasniva na tvrdnji da omjer uspješnih mutacija prema svim mutacijama mora iznositi - ako je omjer manji od tad je nužno smanjiti parametar mutacije , jer je pretpostavka da se bolje jedinke nalaze bliže trenutno raspoloživim jedinkama. Uspješnom se smatra ona mutacija kojom se prikladnost jedinke povećala. U protivnom, treba povećati. Ta se provjera obavlja svakih generacija. Pritom je u jednadžbi (3.17 konstanta iz intervala .

(3.17 )

Jakobović i Golub koriste adaptivan postupak promjene broja mutacija po generaciji [21][22]. Za određivanje mjere trenutnog stanja populacije koriste tri vrijednosti: najveću prikladnost u populaciji, najmanju prikladnost u populaciji i srednju prikladnost . Na temelju njih grade stupanj raznolikosti populacije (degree of population diversity) prema izrazu (3.18).

(3.18)

Stupanj raznolikosti populacije računa se u svakoj generaciji nanovo. Njegova trenutna vrijednost se na početku pohranjuje u varijablu . U svakoj se generaciji stupanj raznolikosti uspoređuje s prethodnom vrijednošću , te se vrijednosti pridružuje trenutni stupanj raznolikosti ako je .

Broj dozvoljenih mutacija po generaciji se tad izračunava prema izrazu (3.19).

(3.19)

Na ovaj se način broj mutacija povećava ako se raznolikost populacije smanji u odnosu na neku najbolju dosad viđenu raznolikost. Vrijednost se za tipične probleme kreće u intervalu .

Prvi primjeri samo-adaptivnog upravljanja pojavili su se u okviru evolucijskih strategija. Evolucijske strategije su slične genetskim algoritmima, i u većini slučajeva koriste prikaz realnim vektorom u koji se dodatno uključuju parametri mutacije. Ideja je da za različite vektore u prostoru rješenja treba koristiti i različite parametre mutacije, te da se za pronalaženje pravih vrijednosti parametara mutacije brine upravo mehanizam selekcije.

Neka je jedinka predstavljena izrazom (3.20). Prvih komponenata vektora predstavlja jedinku, a ostalih komponenata predstavlja parametre mutacija za pripadne komponente jedinke. Poopćenje ovakvog prikaza detaljno je opisano u [1].

(3.20)

Evolucijske strategije prije mutacije jedinke obavljaju mutaciju parametara prema formuli (3.21), gdje je konstanta, a slučajna vrijednost iz distribucije oko nule, a nakon toga obavljaju mutaciju jedinke prema formuli (3.22). Razlog ovom redoslijedu je činjenica da se na ovaj način kasnije, tijekom selekcije, ne evaluira isključivo samo jedinku (jer, evaluacijska funkcija u obzir uzima samo prvih komponenata), već i kvalitetu parametara mutacije koji su doprinijeli stvaranju te jedinke.

	(3.21)
	(3.22)

U ranije spomenutom genetskom algoritmu Smitha i Fogartya [18], koji je za rekombinaciju koristio blokove kromosoma, koristi se sličan princip kao u evolucijskim strategijama – svaki kromosom uz sebe nosi i pripadnu vjerojatnost mutacije. Razlika je u tome što se vjerojatnost mutacije za pojedine blokove računa kao srednja vrijednost vjerojatnosti mutacija svih kromosoma u pojedinom bloku. Ovo je primjer principa koji je potekao iz evolucijskih strategija, a primijenjuje se u okviru genetskih algoritama.

3.5. Selekcija

Prema nekim autorima [1], adaptivni pristup u odabiru roditelja i jedinki za sljedeću generaciju ne koristi se baš često. Ipak, u ovom odjeljku navodimo nekoliko primjera upravljanja parametrima selekcije u okviru genetskih algoritama.

Mnogi postojeći deterministički mehanizmi djelovanja na parametre selekcije temelje se na Boltzmannovoj selekciji kod koje postoji parametar temperature , koji utječe na selekciju i smanjuje se s rednim brojem generacije.

Primjer adaptivnog upravljanja selekcijom predlažu Jakobović i Golub [22]. Prema jednadžbi (3.18) se računa stupanj raznolikosti populacije, te se na temelju njegove trenutne i najveće vrijednosti računa vrijednost prema jednadžbi (3.23).

(3.23)

Jedan od parametara selekcije kojim se upravlja je broj jedinki koja treba zamijeniti na kraju generacije, prema izrazu (3.24), gdje je veličina populacije, a slučajna vrijednost iz intervala . Ako je vrijednost veća, odnosno raznolikost je veća u odnosu na dosad najveću viđenu, i broj jedinki koja treba zamijeniti bit će veći.

(3.24)

Adaptivnost se također primijenjuje na odabir jedinki. Umjesto da koriste funkciju prikladnosti, selekcijski operatori koriste vrijednost , koja se računa prema (3.25), dobivenu na temelju funkcije prikladnosti i vrijednosti .

(3.25)

Ideja iza izraza (3.25) je da se u slučaju visoke raspršenosti populacije kao mjera prikladnosti koristi funkcija prikladnosti, a da se u slučaju visoke konvergencije jedinki više prikladnim smatraju jedinke čija je vrijednost funkcije prikladnosti manja (ovo je moguće ispitati uvrštavanjem vrijednosti 0, 0.5 i 1 za vrijednost ).

Runarsson i Yao [23], a također i Surry i Radcliffe [24], proučavali su rad genetskih algoritama na problemima s ograničenjima, te u tu svrhu razvili metodu stohastičkog rangiranja jedinki kod koje se slučajnim odabirom daje prednost ciljnoj funkciji ili funkciji kazne prilikom rangiranja. Slobodan parametar je ovdje bila vjerojatnost odabira ciljne fukcije kao kriterija za rangiranje, kojom se upravljalo adaptivno. Detaljna analiza njihovog rada prelazi granice ove radnje.

Nije uvijek lako odrediti granice između adaptivnog i samo-adaptivnog upravljanja parametrima. Dobar primjer za to je tzv. Sunburn model opisan u [2], u kojem se traži niz znakova koji kodira svemirski brod u virtualnoj igri. Bez ulaženja u detalje, napomenimo da se za selekciju koristi tzv. gladijatorska turnirska selekcija (gladiatorial tournament selection) kod koje se iz populacije izabiru dva para jedinki, te se jedinke u parovima međusobno evaluiraju borbom. Ishod borbe je pobjeda ili poraz. Par poraženih jedinki se briše iz populacije, dok se iz pobjedničkih jedinki križanjem stvaraju dvije nove. Odabir jedinki u ovom primjeru ne ovisi o funkciji prikladnosti, ni o nekom nepromjenjivom kriteriju, već o trenutnom stanju u populaciji. Neki autori ovakav oblik evolucije nazivaju koevolucijom (coevolution), te ga ne smatraju adaptivnim mehanizmom.

3.6. Veličina i oblik populacije

Parametar vezan uz populaciju koji se najčešće adaptivno mijenja je veličina populacije. Problem odabira najbolje veličine populacije za neki problem zasniva se na činjenici da premale populacije dovode do gubitka stohastičkih svojstava genetskih algoritama i do preuranjene konvergencije, a odabir prevelike populacije ima za posljedicu nepotrebno dugo izvođenje algoritma. Detaljan opis postupaka vezanih uz određivanje veličine populacije dan je u [25].

Treba napomenuti da je za sve vrste adaptivnog upravljanja potreban neki oblik povratne veze. Kod prethodnih je sastavnica genetskih algoritama kao povratna veza služila neka metrika iz populacije. Pokazalo se da je u slučaju upravljanja veličinom populacije najbolja metrika bila ponašanje genetskog algoritma kod druge populacije različite veličine.

Hinterding, Michalewicz i Peachey predložili su adaptivno upravljanje kod kojeg se odjednom nezavisno obavljaju tri genetska algoritma s veličinama populacija postavljenim na 50, 100 i 200. Nakon određenog broja generacija se u svakoj od populacija odabire najbolja jedinka, te se rade promjene u veličini populacija na način da u budućnosti najbolje rezultate daje populacija srednje veličine. Na ovaj se način veličina populacije adaptivno mijenja.

Schlierkamp-Voosen i Mühlenbein [27] predložili su adaptivno upravljanje kod kojeg postoji više populacija, a svaka koristi različiti operator križanja, mutacije ili odabira (ili algoritam pretrage). Tijekom niza generacija populacije evoluiraju neovisno, da bi se nakon određenog broja generacija usporedile. Nakon usporedbe se veličine lošijih populacija smanjuju, a boljih povećavaju, na način da ukupna veličina svih populacija ostane ista, te se dodatno najbolji pojedinci prebacuju u lošije populacije.

Dobar primjer samo-adaptivnog upravljanja veličinom populacije je GAVaPS, kojeg su predložili Arabas, Michalewicz i Mulawka. Umjesto da se odredi neka veličina populacije, svakoj se jedinki pri nastanku pridružuje brojač generacija koje je proveo u generaciji – starost (age) i broj generacija koje će provesti u populaciji – životni vijek (lifetime), koji se odredi na temelju prikladnosti jedinke. Nakon što starost dosegne životni vijek, jedinka se izbacuje iz populacije. Distribucija vjerojatnosti odabira pojedinih jedinki za ulogu roditeljstva je uniformna i ne ovisi o prikladnosti pojedine jedinke. Ideja iza ovoga je da odabir ovisi o životnom vijeku – jedinke koje su duže u populaciji će imati veću vjerojatnost za višestruko roditeljstvo samo zbog svog životnog vijeka.

3.7. Sažetak

U ovom je poglavlju dana podjela metoda za postavljanje parametara. Spomenuta su i četiri kriterija za podjelu metoda upravljanja parametrima – što se mijenja, kako se mijenja, na temelju čega se mijenja i koji je opseg promjene parametara. Potom je naveden niz primjera upravljanja parametrima.

Kod evaluacijske je funkcije ustanovljeno da se adaptacija najčešće koristi kod problema s ograničenjima. Samoadaptivnost evaluacijske funkcije vidljiva je kod problema kod kojih evaluacijska funkcija ovisi o trenutnom skupu jedinki u populaciji, tj. ne postoji neovisna mjera za kvalitetu jedinki.

Primjeri adaptacije kod rekombinacije očituju se u korištenju različitih operatora križanja u različitim populacijama i davanju prednosti onima koji češće dovode do poboljšanja kvalitete jedinki. Čest oblik adaptacije očituje se i davanju prednosti bitovima koji u populaciji prevladavaju, a kao oblik samoadaptivnog upravljanja i praćenje kvalitete bitova s obzirom na sposobnost da dovedu do boljih jedinki.

Uz mutaciju se veže velik broj metoda za upravljanje parametrima. Uz niz determinističkih metoda za promjenu vjerojatnosti mutacije, tu je i niz metoda za upravljanje mutacijom koji se zasniva na praćenju trenutne raznolikosti populacije, kao i poznato Rechenbergovo pravilo. Samoadaptivno upravljanje parametrima mutacije najbolje se očituje u evolucijskim strategijama.

Upravljanje parametrima kod selekcija, te veličine i oblika populacije nešto se rjeđe koriste. Kod selekcije se na temelju trenutne raspršenosti rješenja u populaciji nastoji upravljati selekcijskim pritiskom. Tu se može spomenuti i model starosti jedinki kao alternativa selekciji na temelju funkcije prikladnosti.

Bilo bi izuzetno teško obuhvatiti u istraživanju sve vrste upravljanja parametrima, ili se čak koncentrirati na sve elemente genetskog algoritma koje je moguće mijenjati. Stoga je u daljnjim poglavljima stavljen naglasak na uži skup adaptivnih metoda, te je dokazano da takvi genetski algoritmi funkcioniraju bolje od standardnih.

4. Primjena genetskog algoritma

4.1. Problem trgovačkog putnika

Problem trgovačkog putnika (traveling salesman problem – TSP) pojavio se puno prije nastanka računalne znanosti. Prvi jednu njegovu inačicu razmatra Euler proučavajući problem skakačevog obilaska (knight’s tour problem) još davne 1759. [31]. Problem skakačevog obilaska sastoji se u nalaženju niza poteza skakača tako da sva polja šahovske ploče budu posjećena točno jednom. Stotinjak godina kasnije, Kirkman je proučavao postojanje ciklusa koji posjećuju svaki vrh grafa točno jednom, a Hamilton je postavio tzv. Hamiltonsku igru – problem nalaženja ciklusa u grafu dodekaedra, takvog da je svaki vrh grafa posjećen točno jednom.

Međutim, problem trgovačkog putnika u obliku kakav poznajemo danas razvio se tek 30-ih godina 20. stoljeća, a postavio ga je Karl Menger i nazvao problem glasnika (messenger problem). Taj se problem sastoji u nalaženju najkraćeg obilaska svih točaka iz nekog konačnog skupa za koji je poznata međusobna udaljenost između svake točke. Na problemu su kasnije radili Hassler Whitney i Merril M. Flood sa Sveučilišta u Princeton-u. Tijekom 20. stoljeća, ovaj je problem intenzivno proučavan, te je postao referentni problem za mnoge druge probleme, i za ocjenu kvalitete algoritama za kombinatorne probleme, a njegova rješenja našla su primjene na mnogim područjima.

Definicija 4.1 Problem trgovačkog putnika glasi: za dani broj gradova i cijenu putovanja od bilo kojeg do bilo kojeg drugog grada, koji obilazak svih gradova s povratkom na početni grad ima najmanju cijenu?

Pritom treba primijetiti da u općem slučaju udaljenost od grada A do grada B ne mora nužno biti jednaka udaljenosti od grada B do grada A. Također, za danih gradova veličina prostora rješenja je . Ovo je moguće objasniti na sljedeći način. Pretpostavimo da su gradovi označeni brojevima od do , a da je pojedino rješenje (pojedini obilazak gradova) predstavljeno permutacijom rednih brojeva gradova. Tada bi ukupan broj obilazaka iznosio koliko ima i permutacija niza brojeva duljine , dakle . Međutim, treba primijetiti da je pritom iste obilaske moguće predstaviti s više različitih permutacija. Slika 4.1. pokazuje o čemu je riječ.

Slika 4.1. Različite permutacije za jedan te isti obilazak gradova

Naime, sve četiri permutacije na slici predstavljaju isti obilazak gradova. Rotacijom elemenata pojedine permutacije, obilazak ostaje isti, pa je stoga nužno učvrstiti položaj jednog od gradova, npr. grada s rednim brojem , te potom izbrojati ukupan broj permutacija koje je moguće načiniti. Kako ostaje još elemenata, prostor rješenja je .

Može se pokazati da je problem trgovačkog putnika NP-težak. NP-teški problemi su oni problemi za koje se algoritmi koji ih rješavaju mogu prevesti u algoritam koji rješava bilo koji NP-problem. NP-problem je, pak, svaki problem rješiv u polinomijalnom vremenu pomoću nedeterminističkog Turingovog stroja. Ukratko, nije poznat algoritam koji bi egzaktno riješio problem trgovačkog putnika u polinomijalnom vremenu. Moguće je provesti iscrpnu pretragu, čija je složenost , međutim, ovo je rješenje zbog veličine prostora rješenja nepraktično već za nešto veći broj gradova. Tehnikama dinamičkog programiranja problem je moguće riješiti uz složenost , što je prihvatljivije, međutim, i dalje daleko od idealnog.

4.1.1. Podvrste problema trgovačkog putnika

Kao što je već napomenuto, u općenitom obliku problema trgovačkog putnika, relacija udaljenosti ne mora biti simetrična, tj. udaljenost od grada A do grada B ne mora biti jednaka udaljenosti od grada B do grada A. Takav se TSP naziva asimetrični TSP (assymetric TSP). U praksi je u većini slučajeva relacija udaljenosti simetrična. Međutim, možemo lako smisliti oblike problema kod kojih to nije tako. Dobar primjer za to je traženje obilaska mjesta unutar nekog grada u kojem postoje jednosmjerne ulice – u tom slučaju udaljenost koju treba prijeći od jednog mjesta do drugog, nije jednaka udaljenosti koju je potrebno prijeći od drugog do prvog mjesta.

Oblik TSP-a kod kojeg je udaljenost simetrična relacija naziva se simetrični TSP (symmetric TSP). Prostor rješenja je kod ove podvrste TSP-a upola manji nego kod općenitijeg asimetričnog TSP-a.

Treba primijetiti da kod simetričnog TSP problema neke udaljenosti mogu biti i negativne, što bi označavalo nagradu uslijed putovanja između neka dva grada. Nije teško smisliti primjer za ovo – trgovački bi putnik na nekom putu možda mogao nešto i prodati, i na taj si način smanjiti troškove putovanja.

Nadalje, prirodno ograničenje TSP-a je da relacija udaljenosti bude metrika.

Definicija 4.2 Relacija udaljenosti je metrika ako zadovoljava sljedeća svojstva:

1. Nenegativnost – udaljenost je uvijek veća ili jednaka od nule.

2. Identitet – udaljenost između dva grada jednaka je nuli ako i samo ako se radi o jednom te istom gradu

3. Simetrija – udaljenost od grada A do grada B jednaka je udaljenosti od grada B do grada A za svaki par gradova A i B.

4. Nejednakost trokuta – za svaka tri grada A, B i C, udaljenost između gradova A i C mora biti manja ili jednaka zbroju udaljenosti od grada A do grada B i udaljenosti od grada B do grada C.

Takav TSP naziva se metrički TSP (metric TSP), i on je podvrsta simetričnog TSP-a. Kad postoji metrika, gradovima je umjesto međusobnih udaljenosti moguće pridružiti koordinate i pomoću metrike računati njihovu međusobnu udaljenost. Postoje mnogi primjeri metrika. Jedna od njih je Manhattan metrika koja se računa prema formuli (4.1).

(4.1)

Vrijednost Manhattan metrike jednak je sumi apsolutnih vrijednost razlika koordinata dvaju gradova. Nije teško zamisliti primjer problema gdje je udaljenost određena Manhattan metrikom – na kraju krajeva, Manhattan metrika otud i dobiva svoje ime. Naime, ulice su u velegradovima raspoređene okomito jedna na drugu oko blokova unutar kojih se nalaze zgrade. Udaljenost između mjesta A i mjesta B se pritom ne može računati kao zračna udaljenost, već kao zbroj međusobno okomitih udaljenosti koje treba prijeći. Slika 4.2. prikazuje jedan primjer funkcije udaljenosti u ovoj metrici. Udaljenost je jednaka četiri bloka, što predstavlja zbroj razlika pripadnih koordinata mjesta prikazanih na slici.

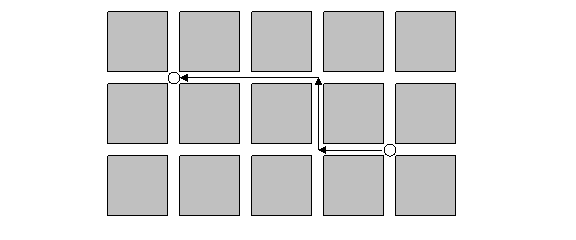
Slika 4.2. Primjer udaljenosti u Manhattan metrici

Euklidski (euclidian) ili planarni (planar) TSP je onaj kod kojeg je udaljenost definirana euklidskom metrikom, čija je formula (4.2). U okviru ovog rada, obavljeni su eksperimenti na euklidskom TSP-u.

(4.2)

4.1.2. Aproksimativne metode

Za problem trgovačkog putnika ne postoje algoritmi polinomijalne složenosti koji daju egzaktna rješenja. Stoga se ovaj problem često rješava pomoću raznih heuristika i aproksimativnih algoritama. Na ovu je temu napisano mnogo radova, i razvijene su mnoge metode. Mnoge heurističke metode rješavanja ovog problema moguće je koristiti u genetskom algoritmu koji rješava ovaj problem. Spomenute su samo neke od njih.

Algoritam najbližeg susjeda (nearest neighbour algorithm) odabire slučajni grad i potom njemu najbliži grad koji nije dio obilaska, te iterativno ponavlja ovaj postupak dok ne oblikuje obilazak svih gradova. Ovaj pohlepni algoritam je prilično jednostavan, međutim, rijetko vodi do optimalnog obilaska, a često je i prilično nedjelotvoran. Štoviše, Gutin, Yeo i Zverovich su u [32] pokazali da postoji beskonačno mnogo instanci problema trgovačkog putnika za koje ovaj algoritam daje, ne podoptimalni, već najduži mogući put. Slika 4.3. prikazuje jedan primjer rada ovog algoritma. Zdesna je prikazan optimalni obilazak, a slijeva onaj dobiven ovim algoritmom. Siva strelica predstavlja povratak u početni grad.

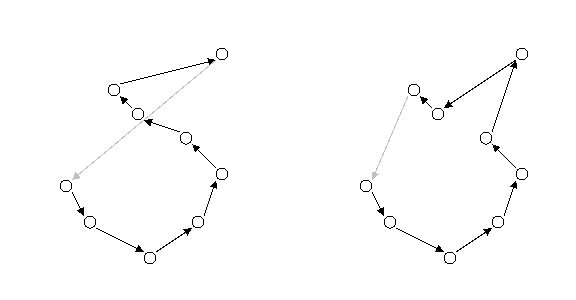
Slika 4.3. Primjer rada algoritma najbližeg susjeda

Heuristika ubacivanja gradova (city insertion heuristic), opisana u [2], odabire tri slučajna grada i stavlja ih u obilazak. Potom, dok god postoji gradova koji još nisu dio obilaska, odabire jedan novi grad i za svaki par susjednih gradova u obilasku izračunava sumu udaljenosti od para gradova do novog grada. Nakon što nađe najmanju sumu udaljenosti, novi grad ubacuje između pripadnog para gradova u obilasku. Ovaj je algoritam u većini slučajeva djelotvorniji od algoritma najbližeg susjeda. Slika 4.4. prikazuje rad ove heuristike i primjer je za slučaj kad i ova heuristika daje podoptimalni obilazak. Sivom je bojom prikazan optimalni obilazak.

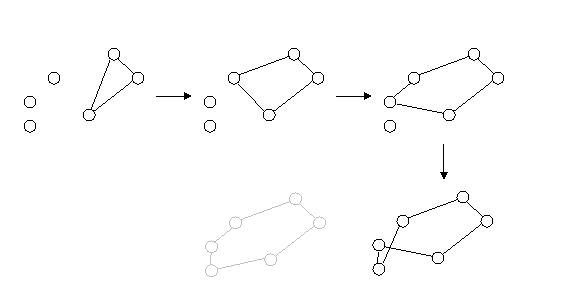
Slika 4.4. Rad heuristike ubacivanjem gradova

Opisane heuristike nazivaju se konstrukcijske (constructive) zato jer rješenje grade malo-pomalo od ničega. Iz tog su razloga primijenjive na inicijalizaciju populacije u genetskom algoritmu – o tome nešto kasnije. Druga grupa heuristika su heuristike iterativnim poboljšanjima (iterative improvement).

Croes je 1958. predložio tzv. 2-opt heuristiku za rješavanje problema trgovačkog putnika. Ona uzima postojeći obilazak gradova i pretražuje sve nesusjedne parove bridova A-B i C-D sa svojstvom da je suma udaljenosti od grada A do grada B i udaljenosti od grada C do grada D veća od sume udaljenosti od grada A do grada C i udaljenosti od grada B do grada D. Kad nađe takav par bridova, u obilasku ih se obriše, a dodaju se bridovi A-C i B-D. Dobiveni obilazak uvijek ima manju ukupnu udaljenost budući da svi ostali bridovi ostaju nepromijenjeni, a novi par bridova imaju manju sumu udaljenosti od starog. Treba primijetiti da je složenost nalaženja svih bridova kod ove metode . Slika 4.5. prikazuje ovu heuristika na djelu – jasno se vidi kako ostatak obilaska ostaje nepromijenjen, dok se udaljenost smanjuje uslijed brisanja starih i dodavanja novih bridova.

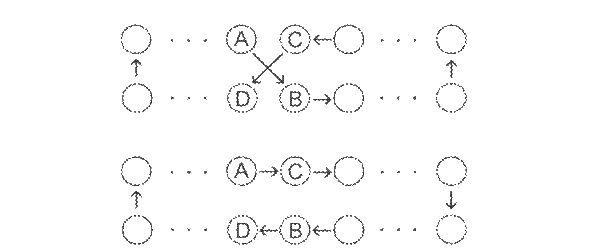
Slika 4.5. Rad 2-opt heuristike

3-opt heuristika radi na sličan način kao i 2-opt heuristika, međutim, ona odabire odabire tri nesusjedna brida A-B, C-D i E-F, te ih preuređuje tako da novonastali bridovi imaju manju sumu udaljenosti od starih. Postupak se potom ponavlja za sljedeću trojku bridova, sve dok više nije moguće naći takvu trojku bridova.

Općenito, postoje k-opt heuristike koje uzimaju bridova i obavljaju ranije opisani postupak. Treba napomenuti da ove heuristike ne vode nužno do optimalnog obilaska, a da je to uvjetovano i redoslijedom odabira k-torki bridova.

Naposljetku, Lin-Kernighan heuristika je jedna od najboljih dosad razvijenih heuristika. Ona iz danog obilaska briše jedan brid, čime nastaje jednostavni put[11]. Jedan od krajeva puta se spaja s nekim od unutarnjih vrhova, a pripadni brid briše. Pritom definiramo sumu dobitka (gain sum) kao zbroj svih obrisanih bridova umanjen za zbroj svih dodanih bridova. Ova dodaj/briši operacija se ponavlja sve dok je suma dobitka pozitivna i postoji još neobrisanih bridova. Pri svakoj dodaj/briši operaciji dobiveni se put spaja u obilazak, te se obilazak pamti ako mu je ukupna udaljenost manja od najbolje dosad viđene. Na kraju se odabire onaj obilazak čija je ukupna udaljenost bila najmanja.

Slika 4.6. Dodaj/briši operacija Lin-Kernighan metode

4.1.3. Primjene problema trgovačkog putnika

Problem trgovačkog putnika je općenita platforma za proučavanje niza metoda koje se mogu primijeniti na širok skup kombinatornih problema. Međutim, i problem trgovačkog putnika sam za sebe ima širok niz primjena [33]. Jedna od prvih primjena bilo je raspoređivanje puteva školskih autobusa koji su vozili djecu, te je poslužila kao motivacija Merrilu Floodu, pioniru u proučavanju TSP-a, za daljnje istraživanje. Sljedeća primjena TSP-a 1940ih odnosila se na transport poljoprivredne opreme, i dovela je do matematičkih istraživanja Mahalanobisa u Bengalu i Jessena u Iowi. Još davno se metodologija rješavanja TSP-a koristila za djelotvorno raspoređivanje kovanica po telefonskim govornicama diljem gradova. U novije vrijeme TSP-om se modelira raspoređivanje servisnih posjeta, dovoženje hrane osobama koje su nepokretne, usmjeravanje transportnih kamiona, itd.

Jednostavnost modela ovog problema dovela je i do njegove primjene na drugim područjima. Klasičan primjer za to je raspored bušenja rupa na tiskanoj pločici. Stroj koji obavlja bušenje rupa mora obići veliki broj mjesta na pločici da bi obavio bušenje. Ako se kao funkcija udaljenosti definira utrošak energije ili vrijeme za micanje glave stroja od jednog do drugog mjesta, onda je cilj taj utrošak ili to vrijeme što više smanjiti – naći obilazak čiji su utrošak ili potrebno vrijeme najmanji. U industriji ovo može višestruko smanjiti troškove proizvodnje. Sličan primjer je raspored pomicanja glave stroja koja otiskuje spojeve na tiskanoj pločici.

Grupa istraživača iz Houstona i sa sveučilišta Brigham Young koristili su ulančanu Lin-Kernighan metodu kako bi optimirali redoslijed udaljenih nebeskih tijela koja bi trebalo slikati u okviru NASA-inog Starlight svemirskog programa. Cilj je bio minimizirati utrošak goriva pri manevrima usmjeravanja dvaju satelita. Ovdje su gradovi bili nebeska tijela koja treba snimiti, a udaljenost između njih utrošak goriva.

Proizvođači poluvodičke tehnologije koristili su metode za rješavanje TSP-a kako bi optimirali testne puteve (scan chains) na integriranom krugu s ciljem što manjeg utroška energije i bržeg rada čipa.

Da TSP ima primjenu i u bioinformatici pokazuje činjenica da je grupa istraživača iz AT&T laboratorija koristila metodologiju rješavanja TSP-a kako bi pronašla najkraći DNA niz dobiven ugrađivanjem DNA nizova (koji se mogu preklapati) iz unaprijed određenog skupa. Istraživači iz američkog Nacionalnog instituta za zdravlje koristili su TSP u svrhu konstruiranja radijacijskih mapa kao dio rada na sekvenciranju genoma.

Bell Telecommunications Research koristio je znanje o TSP-u kao alat za dizajniranje optičkih mreža. Problem trgovačkog putnika se tu vidi u dizajniranju tzv. SONET prstenova koji omogućavaju komunikaciju kroz niz mjesta organiziranih u prsten uz najmanje troškove. U slučaju da veza na nekom mjestu pukne, promet je moguće preusmjeriti u suprotnom smjeru prstena.

Postoji i mnogo drugih kombinatornih problema za koje se može pokazati da su ekvivalentni problemu trgovačkog putnika. Jedan od njih je raspoređivanje poslova na jednom stroju (one-machine scheduling) – problem kod kojeg je poslova nužno naći raspored poslova jednom stroju uz najmanji trošak. Cijena svakog posla ne ovisi samo o prethodnom poslu, već i o rednom broju u rasporedu.

Problem trgovačkog putnika ima mnogo primjena i ovdje su navedene samo neke od njih. Postoji još niz primjera u kojima se TSP pojavljuje kao potproblem - npr. problem usmjeravanja vozila (vehicle routing problem), kao i niz problema koji se mogu svesti na TSP.

4.2. Genetski algoritmi za TSP

Za rješavanje problema trgovačkog putnika korištene su dvije inačice genetskog algoritma – turnirski genetski algoritam (TGA) i generacijski genetski algoritam (GGA). Ulaz svakog od genetskog algoritma je opis problema – popis svih gradova i njihovih koordinata (čime su definirane i međusobne udaljenosti pojedinih gradova, budući da se radi o euklidskom problemu trgovačkog putnika). Izlaz svakog od algoritama je ukupan broj obavljenih iteracija (ili generacija), najjeftiniji nađeni obilazak i njegova cijena. U nastavku su opisane obje inačice.

4.2.1. Implementacija TGA

Korišten je standardni genetski algoritam s turnirskom eliminacijom, a za prikaz rješenja odabran je permutacijski prikaz rješenja. Svako je rješenje prikazano kao niz brojeva od do u kojem se nijedan broj ne ponavlja. Kao što je ranije napomenuto, ovakav prikaz vodi do višestrukih mogućnosti prikazivanja jednog te istog elementa iz prostora rješenja (npr. permutacije i predstavljaju isti obilazak gradova). Ovaj bi se problem mogao riješiti tako da se mjesto jednog od gradova u permutaciji unaprijed odredi, međutim, uz pametan izbor operatora križanja i operatora mutacije, ovaj se problem može zanemariti. Uostalom, višestrukost prikaza jednog te istog rješenja raste linearno s veličinom problema, dok veličina prostora rješenja raste faktorijelno. Ono što je, doduše, bitno za ovakav prikaz je da implementacija operatora križanja i operatora mutacije vodi računa o tome da su permutacije u biti cikličke – u tom smislu, pojam podniz permutacije označava i one nizove unutar permutacije koji, primjerice, počinju sa zadnjih članom permutacije, a završavaju s prvim.

Evaluacijska funkcija je određena sumom udaljenosti između susjednih gradova u permutaciji, s napomenom da se toj sumi dodaje i udaljenost zadnjeg grada u permutaciji od prvog, jer se traže optimalni obilasci. Vrijednost evaluacijske funkcije moguće je odrediti izravno prolaskom kroz pojedinu permutaciju.

Algoritam započinje inicijalizacijom populacije. Početni skup jedinki gradi se nasumično – ne koristi se nikakva heuristika za inicijalizaciju populacije. Pri stvaranju inicijalne populacije, svako od rješenja se ujedno i evaluira. Potom se obavlja glavni dio algoritma sve dok ne istekne unaprijed zadani broj iteracija, ili dok se ne nađe rješenje s unaprijed zadanom očekivanom cijenom. U svakoj iteraciji koristi se turnirska eliminacija na sljedeći način. Slučajnim odabirom izabire se unaprijed zadani broj jedinki. Ovaj broj zove se veličina turnira (tournament size). Dobiveni skup jedinki naziva se turnirski bazen (tournament pool). Potom se pronalazi unaprijed određeni broj najlošijih jedinki u turnirskom bazenu, te se one iz njega izbacuju (otud i naziv turnirska eliminacija). Taj unaprijed određeni broj jedinki koje se izbacuju zove se pritisak (pressure). Pritisak je bilo koji cijeli broj od do veličine turnira umanjene za jedan. Preostale jedinke u turnirskom bazenu slučajnim se odabirom grupiraju u parove i od njih se primjenom operatora križanja grade jednike djeca. Na svako dobiveno dijete se s unaprijed određenom vjerojatnošću primijenjuje operator mutacije. Naposljetku se evaluacijskom funkcijom svakom djetetu pridruži određena cijena. Ovaj se postupak ponavlja sve dok se ne ispuni jedan od dva ranije navedena uvjeta.

4.2.2. Implementacija GGA

Generacijski genetski algoritam može raditi u eliminacijskom ili selekcijskom načinu rada. Eliminacijski način radi tako da u svakoj generaciji iz populacije izbaci određeni postotak jedinki, te izbačene nadomjesti novim jedinkama koje se dobivaju rekombinacijom preostalih. Selekcijski način radi tako da u svakoj generaciji iz trenutne populacije odabire određeni postotak rješenja za narednu generaciju, pr čemu se ista rješenja mogu ponoviti više puta. Nakon toga se populacija za narednu generaciju do kraja popunjava rekombinacijom izabranih rješenja. Nadalje, u oba slučaja generacijski genetski algoritam može primijeniti ili ne primijeniti elitizam. Elitizmom se u svakoj generaciji očuva najbolje nađeno rješenje – na način da se nakon eliminacije ili selekcije najbolje rješenje naprosto ugradi u novu populaciju ako već nije u njoj.

Generacijski genetski algoritam također koristi prikaz rješenja permutacijom. Evaluacijska funkcija definirana je kao i kod TGA – zbrajanjem udaljenosti između uzastopnih gradova u permutaciji.

Kao i TGA, algoritam inicijalizira populaciju stvaranjem slučajnih jedinki, prateći pritom srednju vrijednost evaluacijske funkcije kod svih jedinki, kao i najbolju jedinku. Potom u svakoj generaciji obavlja sljedeći postupak. Najprije izračunava standardnu devijaciju vrijednosti evaluacijske funkcije koja će kasnije biti potrebna za Goldbergovo sigma skaliranje, opisano u 2. poglavlju.

U slučaju da algoritam radi u selekcijskom načinu, za selekciju rješenja za sljedeću generaciju koristi se stohastički univerzalni algoritam za uzorkovanje, poboljšanje algoritma kotača ruleta opisano u 2. poglavlju. Kotač ruleta gradi se tako da bolja rješenja dobivaju veći dio na kotaču ruleta. Najprije se izračuna pomak (bias) prema formuli (4.3), pri čemu je srednja vrijednost evaluacijske funkcije, je standardna devijacija evaluacijske funkcije, a je konstanta čiju je vrijednost postavljena na .

(4.3)

Potom se svakoj jedinki na kotaču ruleta dodjeljuje vrijednost pomaka umanjenog za vrijednost evaluacijske funkcije te jedinke. Ako je ta vrijednost negativna, ona se postavlja na nulu. Vrijednost će biti negativna onda kad je vrijednost evaluacijske funkcije prevelika, odnosno, jedinka je loša.

U slučaju da algoritam radi u eliminacijskom načinu, za eliminaciju lošijih rješenja koristi se algoritam kotača ruleta. Pritom se vrijednosti na kotaču ruleta postavljaju tako da s većom vjerojatnošću budu eliminirane loše jedinke. Pomak se sad računa prema formuli (4.4). Svakoj se jedinki dodijeljuje vrijednost evaluacijske funkcije umanjena za pomak. Ako je ta vrijednost negativna, uslijed visoke vrijednosti evaluacijske funkcije, vrijednost se postavlja na nulu – izrazito dobre jedinke neće biti eliminirane.

(4.4)

Potom se obavlja selekcija ili eliminacija, ovisno o načinu rada. Broj jedniki koje ulaze iz trenutne generacije u sljedeću određen je unaprijed zadanim parametrom algoritma koji se naziva selekcijski pritisak (selection pressure). Jedinke koje su preživjele, ili koje su izabrane za sljedeću generaciju, smještaju se u bazen za rekombinaciju (mating pool). U slučaju korištenja elitizma, najbolja se jedinka također dodaje u bazen za rekombinaciju na slučajnu poziciju. Rekombinacijom se iz preživjelih jedinki populacija popunjava do izvorne veličine. Na svako stvoreno dijete se s određenom vjerojatnošću primijenjuje mutacija. Svakom djetetu odredi se vrijednost evaluacijske funkcije. Naposljetku se prije ulaska u sljedeću generaciju izračunava srednja vrijednost evaluacijske funkcije u populaciji.

4.2.3. Operatori mutacije i križanja

Operatori križanja uglavnom imaju manji utjecaj na svojstva i konvergenciju genetskog algoritma, nego što je to slučaj s operatorima mutacije. Međutim, postoje neke razlike u ponašanju različitih operatora križanja, i one su opisane u ovom odjeljku.

Korišteno je rubno križanje (EX), križanje u poretku (OX), djelomično mapirano križanje (PMX), kružno križanje (CX), pohlepno križanje podobilascima (GSX) i križanje u jednoj točki s djelomičnim očuvanjem (1-PPP). Navedeni operatori križanja opisani su u 2. poglavlju.

Prije svega, treba primijetiti da je problem trgovačkog putnika problem kod kojeg je informacija očuvana u susjedstvu elemenata permutacije (adjacency type problem). To znači da se očekuje da će u većini slučajeva za njega bolje raditi i operatori osmišljeni za takve probleme, a to su PMX i EX. U stvarnosti se, ipak, pokazalo da ovo ovisi od inačice do inačice problema, kao što ćemo vidjeti kasnije.

Operator križanja koji se gotovo uvijek pokazao kao najlošiji za problem trgovačkog putnika je kružno križanje, koje je zamišljeno da očuva koliko je god moguće informacije o apsolutnoj poziciji elemenata. Sjetimo se, kružno križanje u roditeljima traži cikluse – podskupove elemenata koji se nalaze upareni s elementima istog podskupa kad se roditelji postave jedan uz drugog. S druge strane, sjetimo se da je odabrani prikaz rješenja permutacija rednih brojeva gradova, što, kao što je ranije napomenuto, znači da postoji više različitih prikaza za isti obilazak gradova. Dobar operator križanja bi ovo trebao uzeti u obzir.

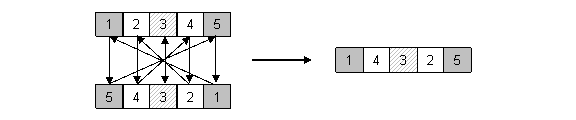
Slika 4.7. Primjer kružnog križanja

Promotrimo, međutim, rezultat kružnog križanja za roditelje i , dvije jedinke koje predstavljaju isti obilazak, za slučaj metričkog TSP-a. Slika 4.7. prikazuje rad kružnog križanja – nalaženje tri ciklusa i stvaranje djeteta naizmjeničnim odabirom ciklusa iz jednog i drugog roditelja. Jasno se vidi da dobiveno dijete više ne predstavlja isti obilazak.

Može se nagađati da iz gore navedenih razloga kružno križanje daje najlošija svojstva u slučaju problema trgovačkog putnika. Korisno je svojstvo svakog operatora da za potpuno iste roditelje vraća dijete potpuno jednako roditeljima, i takav se operator naziva konzervativnim [2].

Definicija 4.3 Operator križanja je konzervativan (conservative) ili čist (pure) ako za potpuno jednaki par roditelja uvijek daje dijete identično roditeljima.

Lako je primijetiti da operator kružnog križanja zaista i je konzervativan. Međutim, mi od operatora križanja tražimo da za jedinke roditelje koje predstavljaju isti obilazak vrate dijete koje predstavlja isti obilazak, što je veći zahtjev na operator. Pomnija analiza pokazala bi da i ostali operatori ne poštuju ovo svojstvo u cjelosti, međutim, ostali operatori su uglavnom stohastički. Križanje u poretku, primjerice, može za segment koji se preslikava odabrati čitavog jednog roditelja, što znači da postoje slučajevi u kojima ono poštuje gore navedeni zahtjev. Kružno križanje nema ovo svojstvo. Drugi bi, dakle, razlog nešto lošijih rezultata ovog operatora mogao imati veze s činjenicom da je ovo deterministički operator – uz isti par roditelja, on uvijek vraća isto dijete.

Operatori koji su posebno zamišljeni za ovu vrstu problema su rubno križanje i djelomično mapirano križanje. Za inačice problema s velikim brojem gradova najbolje se ponašalo rubno križanje. Razlog ovome je što rubno križanje posebno vodi pažnju o tome da se iskoristi informacija o susjedstvu elemenata.

Operatori mutacije imaju velik utjecaj na rad genetskog algoritma, i njegova se svojstva mogu značajno poboljšati pametnim izborom mutacije. Za dobar operator mutacije bitna je i veličina promjene koju on unosi u jedinku. Eksperimentima se može pokazati da operatori koji dovode do manje promjene vrijednosti evaluacijske funkcije jedinke, ujedno i daju bolja svojstva genetskom algoritmu. Dobar primjer takvog operatora je mutacija obrtanjem, budući da ona dovodi do promjene vrijednosti evaluacijske funkcije kod jedinke samo na rubnim dijelovima segmenta kojem se redoslijed elemenata obrće – sjetimo se, kod TSP-a je informacija sadržana u susjedstvu elemenata. Kontraprimjer je mutacija premetanjem, koja dovodi do velikih promjena u genotipu, te doprinosi lošem radu genetskog algoritma.

Postoji još jedno bitno svojstvo operatora mutacije, a to je da oni utječu na povezanost prostora rješenja. Npr. mutacija obrtanjem od permutacije može stvoriti permutaciju . Navedene permutacije su u prostoru rješenja susjedne s obzirom na mutaciju obrtanjem. U slučaju mutacije zamjenom, navedene su permutacije također susjedne. Međutim, s obzirom na mutaciju ubacivanjem, ove permutacije nisu susjedne – ubacivanje je nužno primijeniti dva puta uzastopno da bi se od prve permutacije dobila druga. Definiran je pojam globalnog i lokalnog optimuma [2].

Definicija 4.4 Globalni optimum je element prostora rješenja sa svojstvom da je vrijednost njegove evaluacijske funkcije manja (ili u slučaju funkcije prikladnosti, tj. maksimizacijskih problema, veća) od vrijednosti svih ostalih elemenata u prostoru rješenja. Lokalni optimum je element prostora rješenja sa svojstvom da nijedan niz mutacija tog elementa ne može imati isključivo padajuće vrijednosti evaluacijske funkcije (ili rastuće, u slučaju funkcije prikladnosti).

Treba napomenuti da ono što je lokalni optimum za jedan operator mutacije, ne mora biti lokalni optimum za drugi – razlog tome su razlike u povezanosti prostora rješenja koju uvjetuju različiti operatori mutacije. Eksperimenti jasno pokazuju da genetski algoritam završava u različitim lokalnim optimuma uz korištenje različitih operatora mutacije. Ova je činjenica iskorištena u drugim implementacijama genetskog algoritma koji rješava TSP, opisanim u kasnijim poglavljima.

Korišteni operatori mutacije su zamjena, premetanje, obrtanje, ubacivanje, posmak, višestruki posmak, zamjena segmenata, dvostruko obrtanje, te dva nova operatora specifična za problem trgovačkog putnika – 2-opt operator i pohlepni posmak (GShift).

Treba napomenuti da se svi navedeni operatori križanja i mutacije mogu implementirati uz linearnu prostornu i vremensku složenost. Neke od njih moguće je implementirati i uz konstantnu prostornu složenost.

4.2.4. 2-opt operator

Inspirirani radom Sengokua i Yoshihare [29], razvijen je u okviru ovog rada jedan novi operator mutacije specifičan za problem trgovačkog putnika. Nazvan je 2-opt operator, jer se u svom načinu rada oslanja na 2-opt heuristiku opisanu ranije. Sličan su operator razvili i Sengoku i Yoshihara. Njihov je operator radio tako da provjeri sve parove bridova jedinke i napravi zamjenu tamo gdje je moguće smanjiti cijenu obilaska, baš poput 2-opt metode. Zbog kvadratne složenosti, nastojalo se ovo izbjeći, pa je razvijen novi operator. Slika 4.8. prikazuje pseudokod 2-opt operatora.

Slika 4.8. Pseudokod 2-opt operatora

Iz pseudokoda se jasno vidi da 2-opt operator zapravo obavlja jednu iteraciju 2-opt metode. On odabire jedan brid i uspoređuje ga sa svim ostalima u nadi da će biti moguće smanjiti cijenu obilaska zamjenom bridova. Bitno je primijetiti da se usporedba s ostalim bridovima obilaska uvijek obavlja počevši od nasumičnog brida u obilasku. Ovo je važno zbog stohastičke prirode operatora – da je npr. uvijek započeto s usporedbom brida AB s njemu narednim bridom, tad bi se uvijek obavljala zamjena s istim bridom EF za koji je moguće smanjiti cijenu obilaska. Ovo je neželjeno ponašanje, jer doprinosi zaglavljivanju u lokalnim optimumima. Ideja je da se različite jedinke približavaju različitim lokalnim optimumima, kako bi se očuvao diverzitet populacije i kasnije rekombinacijom iz lokalnih optimuma pobjeglo.

Ako 2-opt ne uspije zamjenom elemenata bridova smanjiti cijenu obilaska, on naprosto obavlja zamjenu dva nasumična elementa u permutaciji. Da ovo ne radi, naprosto bi završio u svom lokalnom optimumu. Na ovaj način obavlja mutaciju koja najvjerojatnije neće poboljšati cijenu obilaska, ali donosi raznolikost u populaciju, što se može pokazati korisnim.

Treba primijetiti i da ovaj način rada 2-opt operatora ima linearnu složenost u ovisnosti o veličini problema (broju gradova). Ovo je svojstvo korisno za probleme s velikim brojem gradova.

Kasnije će biti pokazano da se od svih klasičnih operatora mutacije najbolje ponaša mutacija obrtanjem. Razlog tome je njena sličnost s 2-opt operatorom. Kad 2-opt operator nađe par bridova čijom zamjenom može smanjiti cijenu obilaska, on naprosto obrće redoslijed elemenata između ta dva brida. Mutacija obrtanjem također obrće elemente, ali podniz elemenata koje obrće odabire slučajno, a ne ciljano, kao 2-opt operator. Iz tog razloga genetski algoritam koji koristi 2-opt operator puno brže konvergira k rješenju, ali mutacija obrtanjem ne zaostaje mnogo za njim.

4.2.5. GShift operator

Pohlepni posmak (GShift) radi slično kao i mutacija posmakom. On nasumičnim odabirom izabire podniz elemenata. Potom traži element izvan tog podniza koji je bliži jednom od krajeva ovog podniza, nego što je to njegov trenutni susjed. Kao i 2-opt operator, ovu potragu ne počinje od susjeda, već od nasumičnog elementa u obilasku. Ako nađe takav element, tad odabrani podniz posmiče duž permutacije dok jedan kraj podniza i nađeni element ne postanu susjedni. Ako u tome ne uspije, naprosto odabire nasumično mjesto za posmak, kao što to čini i mutacija posmakom. Slika 4.9. prikazuje njegov rad.

Slika 4.9. Pohlepni posmak

Svojstva ovog operatora pokazala su se boljim od onih klasičnog operatora posmaka, kao što ćemo vidjeti kasnije tijekom rada.

4.3. Eksperimentalni rezultati (TGA)

U ovom ćemo odjeljku opisati eksperimente koji su obavljeni nad turnirskim genetskim algoritmom. Najprije su opisane inačice problema trgovačkog putnika nad kojima su obavljena mjerenja – definirano je nekoliko naših tipova problema, a neki su preuzeti iz drugih radova. Nakon toga su proučeni skupovi parametara genetskog algoritma nad kojima su obavljena mjerenja. Zbog raznolikosti pojedinih inačica, bit će pokazano da ti skupovi nisu sasvim isti za svaku inačicu problema. Naposljetku, prikazani su rezultati ispitivanja, te je dan njihov komentar.

4.3.1. Inačice problema trgovačkog putnika

Korišteno je deset različitih inačica problema i nad njima su obavljena mjerenja. Neki od njih definirani su za potrebe ovog rada, a neki postojeći su preuzeti. Veličine tih problema iznose od do gradova. Tablica 4.1 prikazuje opis korištenih problema.

Tablica 4.1 Ispitni problemi

Ime problema	Veličina problema (u broju gradova)	Duljina najkraćeg poznatog obilaska	Problem preuzet
Spiral50	50	1690	Ne
st70	70	675	Da
kroA100	100	21282	Da
Spiral100	100	1742	Ne
lin105	105	14379	Da
kroA200	200	29368	Da
Spiral250	250	1739	Ne
Multicircular500	500	3687	Ne
rat575	575	6773	Da
pcb1173	1173	56892	Da

Problemi s prefiksom Spiral imaju gradovi posložene u spiralu. Slika 4.10. prikazuje jedan primjer takvog problema i optimalni obilazak tako posloženih gradova. Ostali problemi iz ove skupine izgledaju slično, uz nešto gušću raspodjelu gradova.

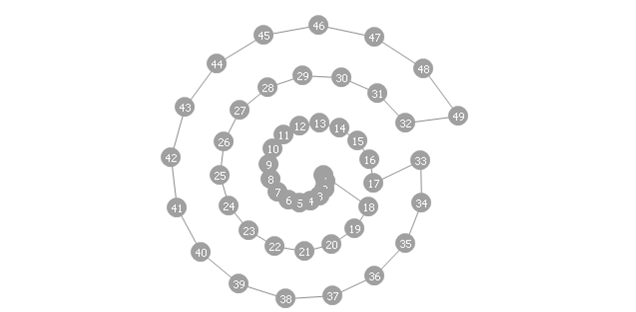
Slika 4.10. Rješenje problema Spiral50

Problem Multicircular500 je još jedan problem koji je definiran za potrebe eksperimentiranja. Gradovi su kod njega posloženi u 3 kružnice. Optimalni obilazak sastoji se od obilaska gradova na unutarnjoj kružnici, prelaska na srednju kružnicu i potom na vanjsku, obilaska gradova na vanjskoj kružnici, prelaska na srednju kružnicu i obilaska gradova na njoj, te povratka na unutarnju kružnicu.

Slika 4.11. Jedno od optimalnih rješenja problema Multicircular500

Problemi st70, kroA100, lin105 i kroA200 imaju nešto manji broj gradova, ali su interesantni zbog velikog broja lokalnih optimuma, i stoga korisni za proučavanje rada genetskog algoritma na njima. Slika 4.12. prikazuje probleme kroA100 i kroA200.

Slika 4.12. Rješenja problema kroA100 i kroA200

Naposljetku, problemi rat575 i pcb1173 imaju velik broj gradova, i posebno su pogodni za mjerenja. Kod manjih inačica problema trgovačkog putnika problematično je što brzina nalaženja rješenja dosta varira budući da se radi o stohastičkom algoritmu, pa rezultati mjerenja nisu toliko pouzdani – ponovno mjerenje često daje nešto drukčije rezultate. Kod većih problema, približavanje rješenju je ujednačenije, pa se na ovakvim problemima i bolje vide svojstva algoritma. Na kraju krajeva, na većim inačicama problema algoritam bi i trebao pokazati svoja dobra svojstva. Slika 4.13. prikazuje rješenje problema pcb1173, poznatog pod nazivom Drilling problem.

Slika 4.13. Rješenje problema pcb1173

4.3.2. Skupovi parametara za mjerenja

U okviru ispitivanja turnirskog genetskog algoritma obavljene su četiri vrste mjerenja. Prije svega, uspoređivane su djelotvornosti različitih operatora mutacije. Pritom je za operator križanja korišteno križanje u poretku, vjerojatnost mutacije je postavljena na , veličinu turnira na , a pritisak na . Tablica 4.2 prikazuje detalje za pojedine probleme.

Tablica 4.2 Vrijednosti parametara za operatore mutacije

Ime problema	Veličina populacije	Broj iteracija	Broj mjerenja
Spiral50, st70, kroA100, Spiral100, lin105, Spiral250	200	1000000	60
kroA200	200	1000000	40
Multicircular500	100	1500000	40
rat575	100	1000000	20
pcb1173	100	1500000	8

Sljedeća vrsta mjerenja odnosila se na usporedbu djelotvornosti različitih operatora križanja. Korišteni operator mutacije pritom je bila mutacija obrtanjem, vjerojatnost mutacije je bila , veličina turnira , a pritisak . Tablica 4.3 prikazuje ostale korištene vrijednosti parametara ovisno o inačici problema. Kao i kod operatora mutacije, za veće inačice problema neki su parametri prilagođeni, kako bi se ostvarila bolja konvergencija algoritma.

Tablica 4.3 Vrijednosti parametara za operatore križanja

Ime problema	Veličina populacije	Broj iteracija	Broj mjerenja
Spiral50, st70, kroA100, Spiral100, lin105, Spiral250	200	1000000	60
kroA200	200	1000000	40
rat575	200	1000000	20
Multicircular500	200	1000000	25
pcb1173	100	1500000	8

Trećom vrstom mjerenja tražena je ovisnost između veličine populacije, vjerojatnosti mutacije i broja obavljenih iteracija. Veličina turnira postavljena je na , a pritisak na . Korišteni operator mutacije bilo je obrtanje, a za operator križanja izabrano je križanje u poretku (OX) i križanje u jednoj točki s djelomičnom očuvanjem (1-PPP). Tablica 4.4 prikazuje korištene vrijednosti parametara.

Tablica 4.4 Vrijednosti za ispitivanje međuovisnosti parametara

Ime problema	Veličina populacije	Vjerojatnost mutacije	Broj iteracija	Križanje	Broj mjerenja
st70, Spiral50	20, 50, 100, 200	0.05, 0.1, 0.3, 0.5	50000, 100000, 200000, 400000	1-PPP	60
kroA100, kroA200	50	0.1, 0.3, 0.5, 0.7, 0.9, 0.95, 0.99	10000 do 400000 uz korak 40000	OX	60
Spiral250	20, 50, 100, 200	0.1 do 0.9 uz korak 0.2	50000, 100000, 200000, 400000	1-PPP	20
Multicircular500	50	0.1 do 0.9 uz korak 0.2	100000, 200000, 500000	OX	12
rat575	10, 20, 50	0.1 do 0.9 uz korak 0.2	100000, 200000, 500000	OX	12
pcb1173	50	0.1 do 0.9 uz korak 0.2	200000, 500000, 1000000	OX	6

Naposljetku, četvrtom vrstom mjerenja proučavano je ponašanje turnirskog genetskog algoritma koji koristi 2-opt operator mutacije. Ovo je mjerenje obavljeno na problemu pcb1173. Pritom je korišteno križanje u poretku, veličina populacije bila je , veličina turnira , pritisak , vjerojatnost mutacije mijenjana je od do u koracima od , a broj iteracija od do u koracima od . Napravljena su pritom mjerenja.

Za sve četiri vrste mjerenja praćena izlazna vrijednost bila je cijena najboljeg nađenog obilaska – u obzir se uzimala srednja vrijednost nakon više mjerenja. Alternativa je bila pratiti broj potrebnih iteracija da bi se dostigla neka unaprijed određena cijena, međutim, utvrđeno je da ova vrijednost ima veće rasipanje nego dostignuta cijena nakon unaprijed određenog broja iteracija, i iz tog razloga je izbjegnuta.

4.3.3. Rezultati i komentar eksperimenata

U ovom su odjeljku prikazani rezultati sve četiri vrste mjerenja. Prikazani su grafovi na kojima se vide odnosi između različitih operatora i različitih vrijednosti parametara.

Operatori rekombinacije. Kao što je spomenuto, operatori rekombinacije imaju manji utjecaj na rad genetskog algoritma nego operatori mutacije. Međutim, korisno ih je usporediti i odrediti koji operator za većinu inačica problema daje najbolje rezultate. Očekivano je da će to biti rubno križanje, s obzirom da je ono posebno osmišljeno da čuva informaciju u susjedstvu elemenata (kao susjedni element u djetetu postavlja najprije onaj koji je zadnje dodanom elementu susjedan u oba roditelja, a tek onda onaj susjedan u tek jednom od roditelja). Slika 4.14. prikazuje rad operatora križanja na manjim inačicama problema trgovačkog putnika (slijeva nadesno, red po red). Kao što se može vidjeti s grafova, razlike u cijeni najboljeg nađenog obilaska nisu velike – operatori križanja ne igraju veliku ulogu. Međutim, ono što se također može primijetiti je opetovana prednost križanja u jednoj točki s djelomičnim očuvanjem. Za manje probleme ovaj je operator očito veoma dobar. Dodatno, u većini mjerenja kružno se križanje, kao što je ranije nagoviješteno i objašnjeno, pokazalo kao najlošiji operator križanja.

Slika 4.15. prikazuje rad operatora križanja za veće inačice problema trgovačkog putnika. Kao što je ranije napomenuto, a što se sad i jasnije vidi s grafova, veće su inačice problema pogodnije za mjerenja, jer imaju manje rasipanje vrijednosti – dostignuta cijena konzistentnija je iz mjerenja u mjerenje. Oblici grafova su konzistentniji kako se ide prema većim inačicama problema i sve više poprimaju svoj karakteristični oblik, a može se primijetiti da je, sukladno očekivanjima, najbolji operator križanja upravo rubno križanje. Uvjerljivo najlošije je, kao i ranije, kružno križanje.

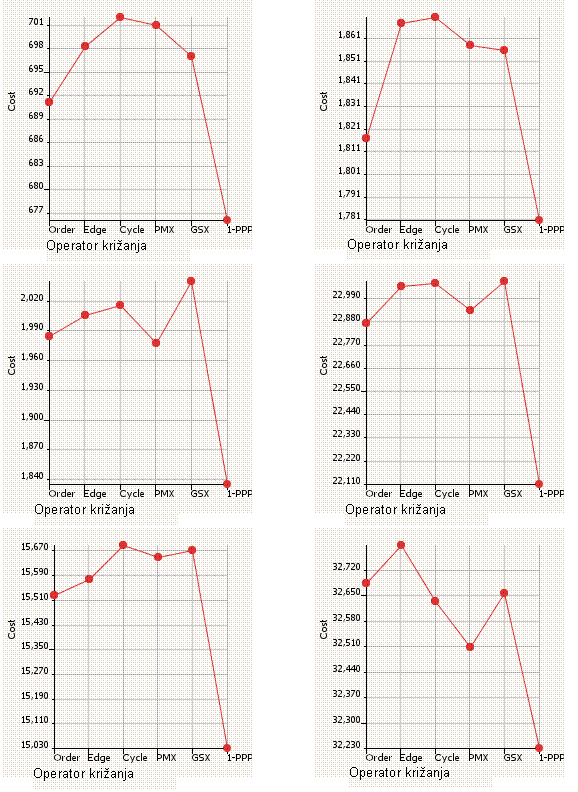
Slika 4.14. Djelotvornost operatora križanja za st70, Spiral50, Spiral100, kroA100, lin105 i kroA200 (manje je bolje)

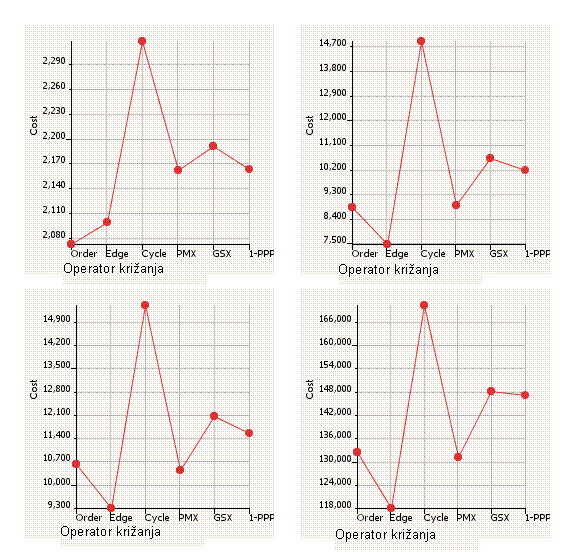
Slika 4.15. Djelotvornost operatora križanja za Spiral250, Multicircular500, rat575 i pcb1173 (manje je bolje)

Operatori mutacije. Kao i kod operatora križanja, za manje se inačice problema teže da naslutiti koji je operator najbolji. Slika 4.16. prikazuje tipične primjere – bitku za pobjedu vode 2-opt, pohlepni posmak i dvostruko obrtanje. Slika 4.17. pokazuje sličnu situaciju na ostalim manjim inačicama problema, međutim, sad mjesto najboljeg operatora napadaju i obrtanje, posmak i višestruki posmak. Iz ovoga je nejasno kako toliko hvaljeni 2-opt operator može biti toliko dobar – razlog tome je što je za manje inačice problema dan dovoljan broj iteracija i lošijim operatorima da nađu rješenje. U svakom slučaju, mutacija zamjenom i mutacija premetanjem daju konzistentno loše rezultate.

Slika 4.18. prikazuje rad operatora mutacije na većim inačicama problema. Kao i kod križanja, tek se ovdje pojavljuju karakteristični oblici grafova. Ovdje je trijumf 2-opt operatora jasno vidljiv, a za petama su mu pohlepni posmak i njemu srodna mutacija obrtanjem.

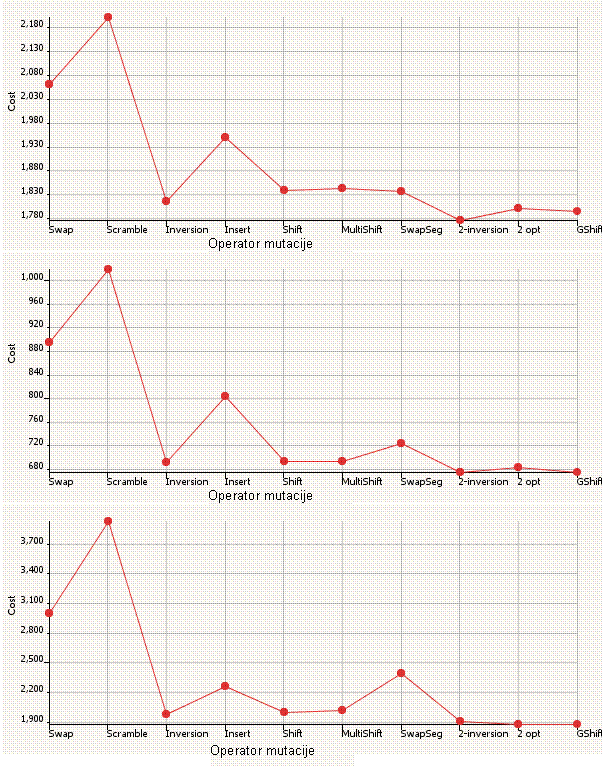
Slika 4.16. Djelotvornost operatora mutacije za Spiral50, st70 i Spiral100 (manje je bolje)

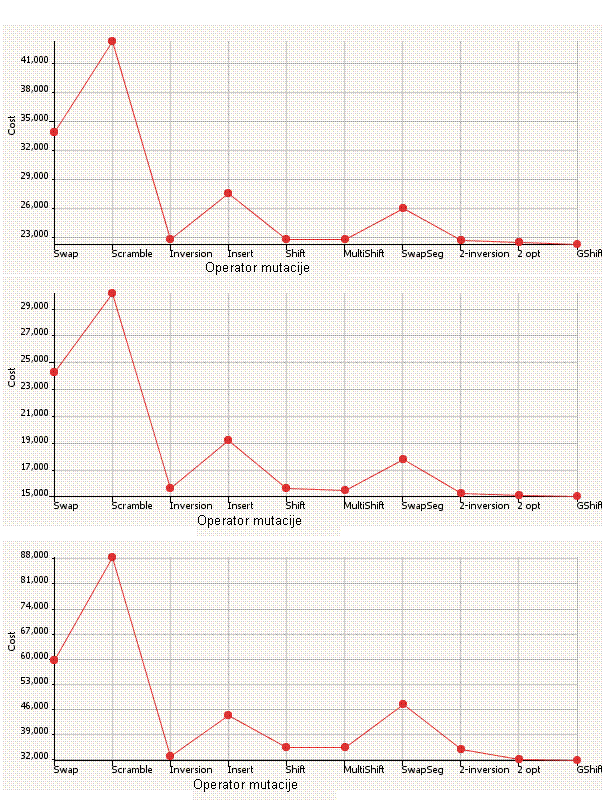
Slika 4.17. Djelotvornost operatora mutacije za kroA100, lin105 i kroA200 (manje je bolje)

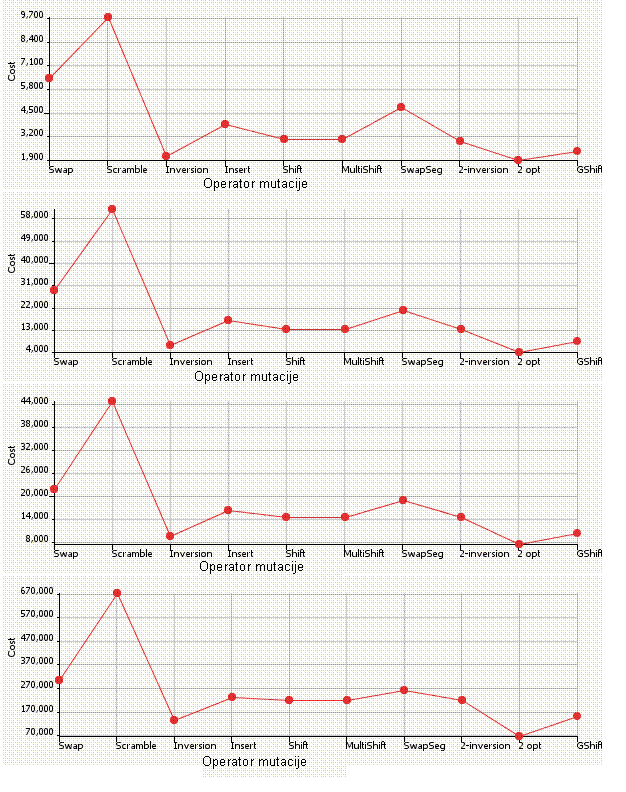
Slika 4.18. Djelotvornost operatora mutacije za Spiral250, Multicircular500, rat575 i pcb1173 (manje je bolje)

Razlozi lošeg ponašanja mutacije premetanjem opisani su ranije – pokazuje se da svojstvo povezanosti čitavog prostora rješenja nije dobro, barem ne za ovaj tip problema. Što se tiče mutacije zamjenom, može se nagađati da povezuje elemente prostora rješenja na način koji vodi do postojanja velikog broja lokalnih optimuma. Objašnjenje može biti sljedeće: u radu genetskog algoritma koji rješava problem trgovačkog putnika, lako se može zamijetiti postojanje podnizova u trenutno najboljem obilasku takvih da su oni već optimalni i ne treba ih mijenjati, već naprosto čitave pomicati po permutaciji. Mutacija zamjenom za ovo naprosto nije sposobna – ona takve već optimalne segmente mora pomicati element po element, čime u velikoj većini slučaja ujedno i povećava cijenu obilaska. Prema ranijoj definiciji, ovo predstavlja upravo lokalni optimum u prostoru rješenja, jer je potrebno obaviti niz mutacija, a ne jednu, kako bi se prikladnost jedinke povećala. Uostalom, treba primijetiti da svi ostali operatori (pa čak i mutacija ubacivanjem!) koji rade relativno dobro, rade upravo s čitavim segmentima, a ne s pojedinačnim elementima.

Vjerojatnost mutacije, veličina populacije i broj iteracija. Posebno velik broj mjerenja obavljen je u ovom eksperimentu, stoga nisu prikazani svi dobiveni grafovi, već samo neki. Slika 4.19. prikazuje kako cijena najboljeg dobivenog obilaska ovisi o vjerojatnosti mutacije za problem kroA100. Prikazane su tri krivulje, i može se sukladno očekivanjima primijetiti da je ova krivulja niže za veći broj iteracija. Nadalje, sa slike se očituje da optimalna vrijednost vjerojatnosti mutacije nije neovisna o broju obavljenih iteracija. Ako se obavi veći broj iteracija, optimalna vrijednost vjerojatnosti mutacije je veća. Može se pretpostaviti da je razlog tome što jednom kad se algoritam, nakon većeg broja obavljenih iteracija, približi rješenju, a populacija konvergira, za stvaranje novih jedinki odgovorna je pretežno mutacija, pa veća vjerojatnost mutacije povećava i vjerojatnost nalaženja boljeg rješenja.

Na istoj se slici vidi i ovisnost cijene najboljeg nađenog obilaska o broju učinjenih iteracija. Ovo je dobro poznata krivulja s karakterističnim koljenom na početku grafa, i ne razlikuje se mnogo od inačice do inačice problema, stoga je prikazana samo za ovaj problem. Na grafu je prikazana familija krivulja, od kojih koljeno najniže ima ona s vjerojatnošću mutacije .

Problem Spiral250 ima nešto veći broj gradova i pogodan je za eksperimente. Slika 4.20. prikazuje ovisnost cijene najboljeg obilaska o vjerojatnosti mutacije za familije krivulja kod kojih se na jednom grafu mijenja broj iteracija, a na drugom veličina populacije. Vidi se da je za male populacije optimalna vrijednost vjerojatnosti mutacije nešto viša (oko za veličinu populacije ). Naime, kod malih populacija mutacija igra veću ulogu, radi unošenja novog genetskog materijala u populaciju, dok veće populacije imaju i veću količinu genetskog materijala same po sebi, pa je optimalna vrijednost vjerojatnosti mutacije nešto niža.

Interesantno je promatrati vezu između cijene najboljeg obilaska i veličine populacije. Slika 4.21. prikazuje kako je u slučaju manjeg broja iteracija algoritma bolja što manja populacija. Međutim, kako broj iteracija raste, cijena najboljeg obilaska kod većih populacija postaje sličnija ovoj kod manjih – krivulja je manje nakošena. Manje populacije brže dovode do rješenja, međutim, kod njih postoji veća vjerojatnost zaglavljivanja algoritma u lokalnom optimumu.

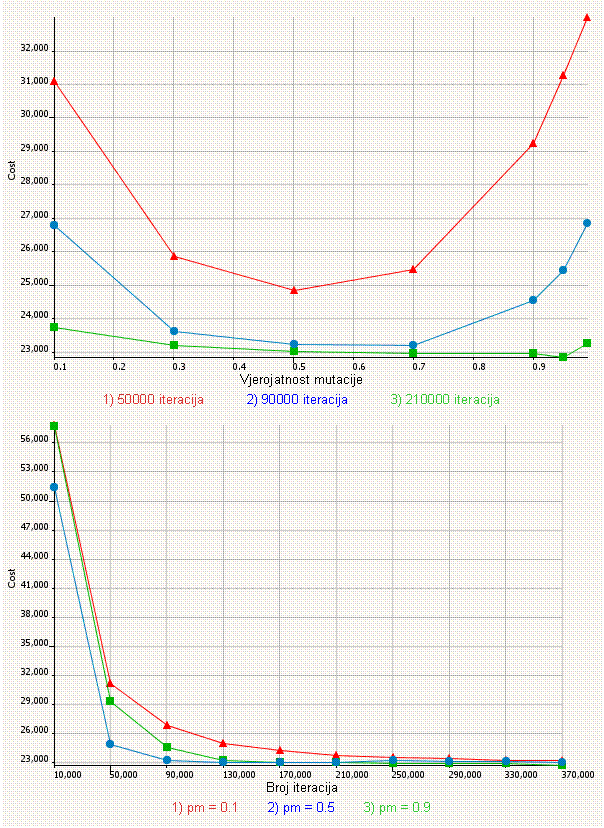
Slika 4.19. Ovisnost cijene o vjerojatnosti mutacije i broju iteracija za kroA100

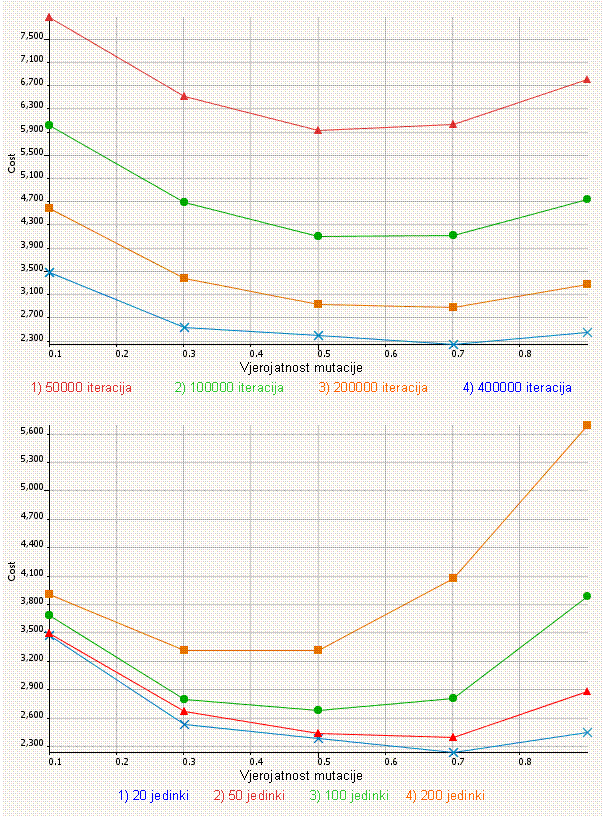
Slika 4.20. Ovisnost cijene o vjerojatnosti mutacije za Spiral250

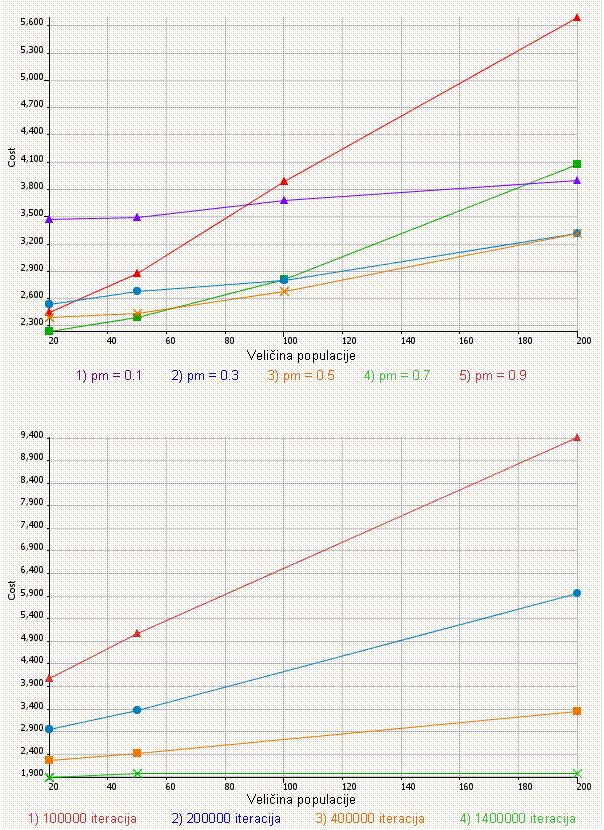
Slika 4.21. Ovisnost cijene o veličini populacije za Spiral250

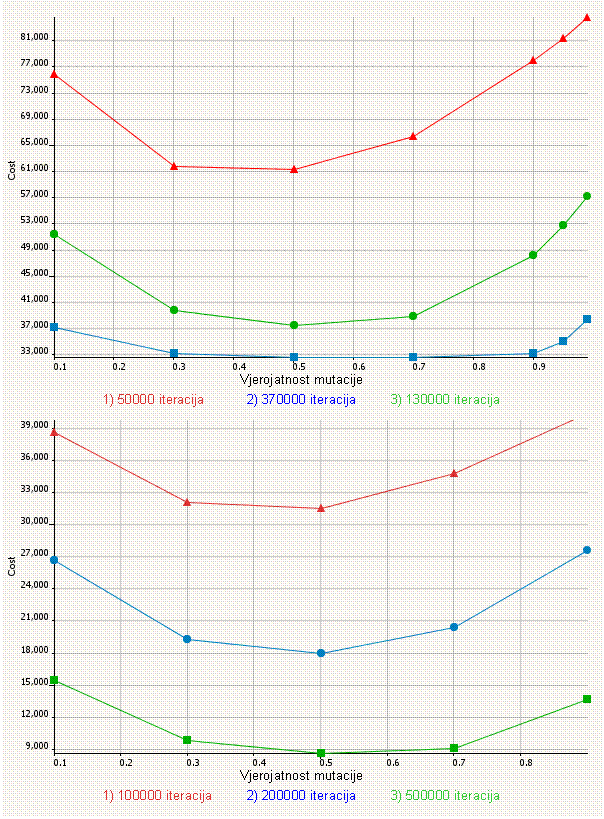
Slika 4.22. Ovisnost cijene o vjerojatnosti mutacije za kroA200 i Multicircular500

Slika 4.23. Ovisnost cijene o vjerojatnosti mutacije za rat575 i pcb1173

Može se primijetiti da je za većinu problema optimalna vrijednost vjerojatnosti mutacije između i . Ovo, naravno, ovisi i o ostalim parametrima genetskog algoritma – veći broj iteracija uvjetuje i veću optimalnu vjerojatnost mutacije. Slika 4.23. prikazuje primjer za ovo – kod problema pcb1173 za iteracija optimalna je vrijednost vjerojatnosti mutacije oko . Međutim, za iteracija, optimalna vjerojatnost mutacije je oko .

Slika 4.25. prikazuje ovisnost cijene o veličini populacije i vjerojatnosti mutacije redom za probleme kroA100, kroA200, Spiral250, MultiCircular500, rat575 i pcb1173.

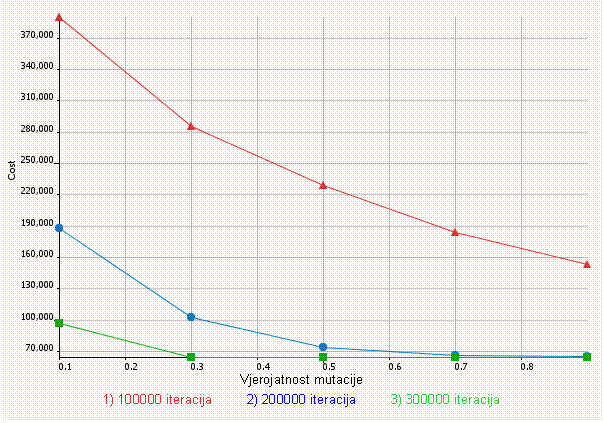
Slika 4.24. Ovisnost cijene o vjerojatnosti mutacije kod 2-opt operatora

Vjerojatnost mutacije za 2-opt operator. Kako se u slučaju 2-opt operatora radi o heurističkom operatoru koji je osmišljen specifično za ovaj problem, i koji većini jedinki povećava vrijednost evaluacijske funkcije, isplatilo se proučiti koje su optimalne vrijednosti za vjerojatnost mutacije u pripadnom genetskom algoritmu. Pokazalo se da za njega optimalne vrijednosti ne leže na sredini oko , već se nalaze oko , što se moglo i očekivati. Naime, skoro svaka primjena 2-opt operatora dovodi do povećanja kvalitete jedinke, stoga algoritam uvijek brže nalazi rješenje ako se 2-opt češće koristi. Slika 4.24. prikazuje navedenu ovisnost.

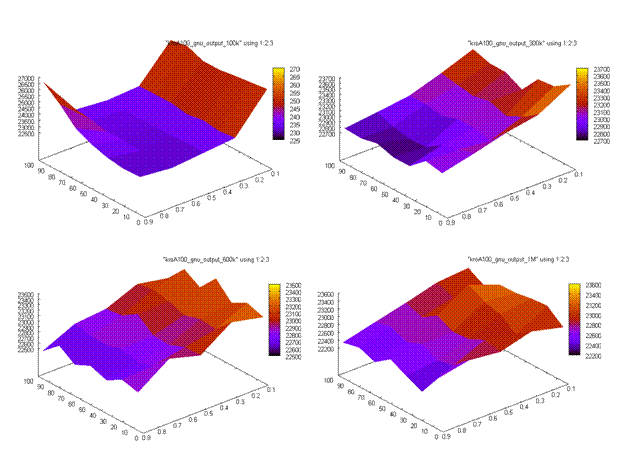
Slika 4.25. Ovisnost cijene o veličini populacije i vjerojatnosti mutacije za kroA100

Slika 4.25. prikazuje ovisnost cijene najboljeg pronađenog obilaska o veličini populacije i vjerojatnosti mutacije, redom za broj iteracija , , i iteracija. Prikaz je, zbog dvije ulazne varijable, trodimenzionalan, pa optimalni skup parametara nalazimo na onoj točki plohe u kojoj se nalazi minimum. Na prvoj se slici vidi da se najmanja cijena obilaska nalazi za izrazito male populacije, i visoke vjerojatnosti mutacije. Međutim, uz nešto veći broj iteracija, može se primijetiti da algoritam uz malu veličinu populacije redovito zaglavi u lokalnom optimumu.

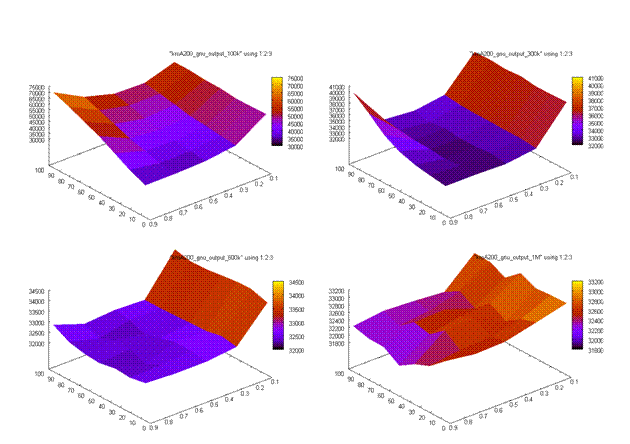
Slika 4.26. Ovisnost cijene o veličini populacije i vjerojatnosti mutacije za kroA200

Slika 4.26. prikazuje istu ovisnost za problem kroA200. Pri manjem broju iteracija je ponašanje algoritma slično kao i za kroA100. Uz nešto veći broj iteracija, opet se može primijetiti da pretraga za male veličine populacija zastaje u lokalnom optimumu. Optimalni skup parametara za 100 tisuća iteracija nalazimo kod populacije veličine 5 i vjerojatnosti mutacije između 0.5 i 0.7, dok je za 1 milijun obavljenih iteracija optimalni skup parametara pri veličini populacije 50 i vjerojatnost mutacije 0.9.

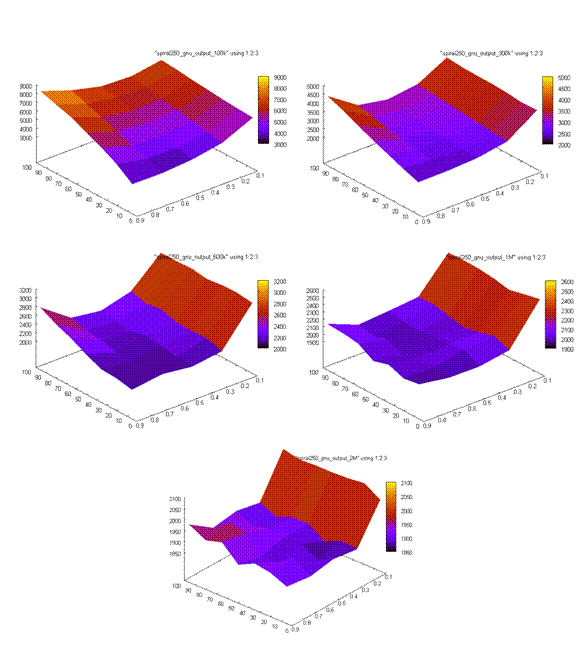
Slika 4.27. Ovisnost cijene o veličini populacije i vjerojatnosti mutacije za Spiral250

Za probleme Spiral250 i rat575 najbolje su rezultati postignuti uz najmanju veličinu populacije i visoku vjerojatnost mutacije. Uz veći broj iteracija može se pokazati da uz male populacije pretraga zastaje u lokalnom optimumu zbog preuranjene konvergencije, kao što je to slučaj kod manjih inačica problema. Slika 4.27. prikazuje prijašnju ovisnost za problem Spiral250. Jasno se nazire slično ponašanje algoritma kao i ranije – za manji broj iteracija pogodnije su manje populacije i visoka vjerojatnost mutacije, dok je kod većeg broja iteracija pogodnije imati veće populacije radi izbjegavanja preuranjene konvergencije. Za slučaj 2 milijuna iteracija (posljednji graf), optimalni skup parametara ima veličinu populacije 35, a vjerojatnost mutacije 0.3. Sve ovo navodi na zaključak da je optimalni skup parametara specifičan ne samo za konkretan problem koji se rješava genetskim algoritmom, već i za inačicu problema.

Kod problema rat575 ustanovljeno je da je za 500 tisuća, 1,5 milijuna i 2,5 milijuna iteracija najbolji skup parametara onaj s minimalnom veličinom populacije i visokom vjerojatnošću mutacije. Kako se radi o inačici problema s velikim brojem gradova, tek bi uz puno veći broj iteracija dobili neki drugi optimalni skup, kao što je to slučaj kod manjih inačica problema.

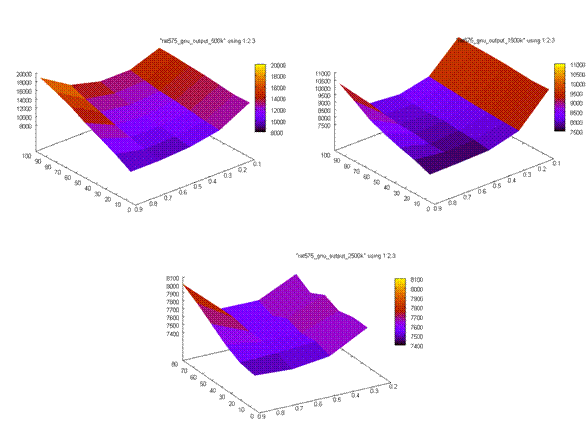
Slika 4.28. Ovisnost cijene o veličini populacije i vjerojatnosti mutacije za rat575

5. Primjena adaptivnog genetskog algoritma

U ovom je poglavlju opisan adaptivni turnirski genetski algoritam (ATGA) i objašnjeno je zašto on u dosta slučaja daje bolje rezultate od običnog turnirskog genetskog algoritma. Potom su navedene tvrdnje opravdane eksperimentalnim rezultatima.

5.1. Adaptivni turnirski genetski algoritam (ATGA)

Adaptivni turnirski genetski algoritam je prilagodba turnirskog genetskog algoritma opisanog u 4. poglavlju. On radi na potpuno isti način kao i TGA, s razlikom da po isteku određenog broja iteracija obavlja promjenu vrijednosti nekih parametara. U 3. smo poglavlju vidjeli pregršt metoda za promjenu vrijednosti parametara, i utvrdili da nije praktično koristiti više od nekoliko navedenih metoda. U ovom radu koncentrirali smo se na promjenu vrijednosti parametara vezanih uz mutaciju.

5.1.1. Krajolik funkcije prikladnosti

U slučaju problema kod kojih je prikaz rješenja dan realnim vektorom, nije teško zamisliti krajolik funkcije prikladnosti (fitness landscape). Svakom je vektoru pridružena neka vrijednost funkcije prikladnosti, te na taj način nastaje krajolik funkcije prikladnosti, te globalni i lokalni optimumi. U slučaju prikaza rješenja permutacijom, krajolik funkcije prikladnosti više nije tako intuitivan pojam. Definiran je, stoga, krajolik funkcije prikladnosti.

Definicija 5.1 Krajolik funkcije prikladnosti za prikaz rješenja permutacijom je graf čiji skup vrhova određuju sve smislene permutacije, a čiji su bridovi svi oni bridovi između vrha A i vrha B takvi da je iz permutacije predstavljene vrhom A moguće mutacijom dobiti permutaciju predstavljenu vrhom B i obratno.

Smislene permutacije pritom označavaju sve permutacije koje zaista predstavljaju neko rješenje. U slučaju problema trgovačkog putnika, ovo su sve permutacije od elemenata, no to općenito ne mora biti tako za svaki problem. Nadalje, iz navedene se definicije može zamijetiti da je krajolik funkcije prikladnosti uvjetovan operatorom mutacije – kao što je u 4. poglavlju objašnjeno da operator mutacije uvjetuje povezanost prostora rješenja. U skladu s definicijom iz 4. poglavlja, lokalni optimum u prostoru rješenja je rješenje kojem prikladnost nije moguće poboljšati isključivo jednom bilo kojom mutacijom. Iz ove je definicije jasno da je lokalni optimum u krajoliku funkcije prikladnosti vrh kojem svi susjedi imaju nižu vrijednost funkcije prikladnosti. Kako neki drugi operator mutacije ne mora imati iste susjede, tako taj vrh ne mora ni biti lokalni optimum.

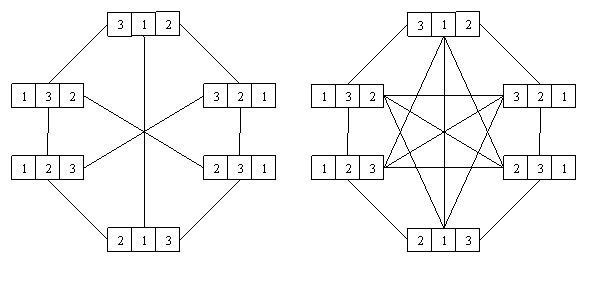
Slika 5.1. Povezanost permutacija reda 3 za mutacije zamjenom i premetanjem

Slika 5.1. prikazuje primjer povezanosti za mutacije zamjenom i premetanjem za permutacije reda 3. Na lijevom grafu su susjedni vrhovi oni čije se permutacije mogu dobiti jedna iz druge zamjenom pozicija pojedinačnih elemenata. Na desnom su grafu svi vrhovi susjedni, budući da je premetanjem elemenata jedne permutacije moguće dobiti bilo koju drugu permutaciju. Za permutacije viših redova grafovi su mnogo veći. Već za permutacije reda 5 pripadni bi graf imao 120 vrhova. Kad bi se željelo prikazati krajolik funkcije prikladnosti kao graf u trodimenzionalnom prostoru kod kojeg visina pojedinog vrha ilustrira vrijednost njegove funkcije prikladnosti, dobila bi se veoma zamršena i nejasna sliku. Dan je stoga samo umjetnički prikaz krajolika funkcije prikladnosti. Slika 5.2. prikazuje jedan mogući primjer dijela krajolika prikladnosti. Na prvoj slici dan je krajolik za jedan operator mutacije, te se jasno nazire da je vrh zdesna lokalni optimum. Međutim, neki drugi operator mutacije daje drugačiju povezanost vrhova, pa na desnoj slici isti vrh više nije lokalni optimum, jer ima susjeda čija je prikladnost veća od njegove vlastite.

Slika 5.2. Umjetnički prikaz krajolika funkcije prikladnosti

Jednom kad pretraživanje zaglavi u lokalnom optimumu, potrebno je obaviti točno određeni niz mutacija kako bi se došlo do vrha s većom vrijednošću funkcije prikladnosti. S obzirom da pritom nastaju jedinke niže kvalitete, velika je vjerojatnost da će te jedinke biti eliminirane, te da niz mutacija koji vodi do jedinke veće prikladnosti neće biti uspješno obavljen. Međutim, promjenom krajolika funkcije prikladnosti, moguće je trenutno se naći u vrhu koji više nije lokalni optimum. Zaključak svega ovoga je da mudra i pravovremena promjena operatora mutacije može dovesti do bijega iz lokalnog optimuma.

5.1.2. Efekt kombinacije mutacije posmakom i mutacije obrtanjem

Tvrdnje iznesene u prethodnom odjeljku trebalo bi opravdati konkretnim primjerima. Potrebno je naći takvu kombinaciju operatora mutacije da lokalni optimumi jednog operatora nisu lokalni optimumi za drugi operator. Ovo, naravno, ovisi i o konkretnoj inačici problema, pa bi trebalo naći takav par operatora da ovo vrijedi barem za dosta inačica problema.

Proučavajući lokalne optimume u kojima završava pretraga za MultiCircular tipove problema opisane ranije, uz korištenje mutacije obrtanjem, otkriven je takav par operatora. Slika 5.3. prikazuje primjer globalnog i lokalnog optimuma za mutaciju obrtanjem. Da bi se pobjeglo iz lokalnog optimuma (za obrtanje) prikazanog zdesna, potrebno je obaviti više od jedne mutacije obrtanjem. Za neki drugi operator ovo ne mora biti lokalni optimum. Pokazalo se da je taj operator upravo mutacija posmakom.

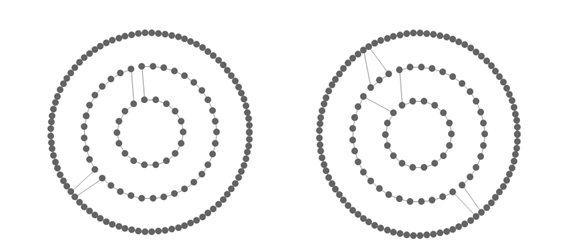
Slika 5.3. Primjer globalnog i lokalnog optimuma za mutaciju obrtanjem

Slika 5.4. prikazuje još jedan lokalni optimum za ovaj tip problema. Permutacija koja se nalazi slijeva, dobivena uz korištenje mutacije obrtanjem, predstavlja taj lokalni optimum. Zdesna je prikazana nova permutacija nakon posmaka elemenata . Novonastali bridovi otisnuti su masno. Osim što novodobivena permutacija ima očito manju cijenu, može se primijetiti da jednostavno obrtanje elemenata dovodi do permutacije s još manjom cijenom. Obje su permutacije raspisane ispod njihovih slika.

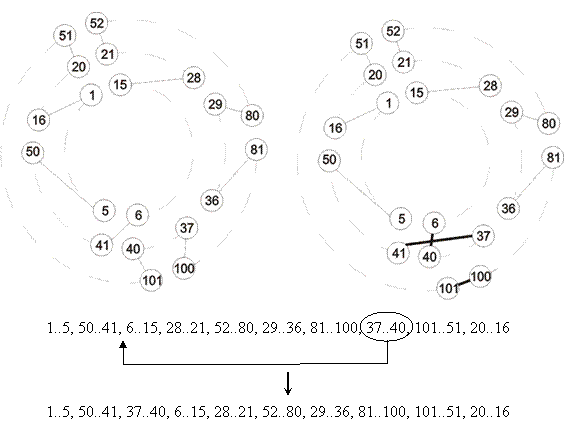
Slika 5.4. Primjena mutacije posmakom Multicircular tip problema

Navedeni primjer ukazao je na mogućnost da su mutacija obrtanjem i mutacija posmakom par operatora koji dobro surađuju. Ostaje otvoreno pitanje da li je ovaj tandem operatora dobar i za ostale inačice problema trgovačkog putnika.

U adaptivnoj inačici turnirskog genetskog algoritma iskorišteno je ovo promatranje, što se pokazalo korisnim. Kombinacija više operatora, uz njihovu pravovremenu izmjenu, povećava djelotvornost genetskog algoritma. Kombinacija navedenog para operatora pokazala se posebno dobrom, kao što ćemo vidjeti kasnije.

5.1.3. Korištene adaptivne metode

U adaptivnom turnirskom genetskom algoritmu korišteno je više adaptivnih mehanizama, od kojih su se neki pokazali više, a drugi manje djelotvornima. Neki samo lagano smanjuju broj iteracija potreban za dostizanje rješenja, dok drugi omogućavaju lakši bijeg iz lokalnih optimuma. Korištene adaptivne metode orijentirane su na promjenu vrijednosti vjerojatnosti mutacije, te na promjenu korištenih operatora mutacije. Za sve metode koristi se unaprijed definirani parametar nazvan perioda adaptacije (adaptation period). Ovaj parametar određuje broj iteracija koji mora proteći prije nego što se obavi neka prilagodba.

Variranje vjerojatnosti mutacije (mutation probability varying). Ova metoda prati broj iteracija koji je protekao od zadnjeg povećavanja prikladnosti najbolje jedinke u populaciji. Ako je taj broj veći od periode adaptacije, vjerojatnost mutacije se uveća za unaprijed definiranu vrijednost parametra nazvanog povećanje vjerojatnosti mutacije (mutation probabiliy increase), a vrijednost brojača se postavlja na nulu. S druge strane, ako je broj iteracija od povećanja prikladnosti najboljeg rješenja u populaciji jednak nuli, ili, drugim riječima, ako je upravo nađeno bolje rješenje, tad se vjerojatnost mutacije umanjuje za osmerostruko uvećanu vrijednost povećanja vjerojatnosti mutacije. Pritom vrijedi pravilo da vjerojatnost mutacije ne smije biti manja od inicijalne ni veća od . Na ovaj način se vjerojatnost mutacije povećava ako pretraga zaglavi u lokalnom optimumu, a smanjuje u slučaju da pretraga napreduje.

Prilagodljiva izmjena operatora (adaptive operator cycling). Ova se metoda oslanja na unaprijed definiranu listu operatora mutacije za zamjenu. Tijekom svog rada izmijenjuje operatore mutacije definirane na toj listi, a to čini stohastički na temelju njihove uspješnosti.

Prilagodljiva izmjena operatora pokreće se kad vrijednost posebnog brojača iteracija postane veća od perioda adaptacije, uz uvjet da je u međuvremenu obavljena barem jedna mutacija. Potom se izračunava omjer broja uspješnih i ukupnog broja mutacija , pri čemu se uspješnom mutacijom smatra ona nakon čije primjene se prikladnost jedinke povećala. Nakon toga se izračunava vjerojatnost promjene operatora mutacije prema formuli (5.1).

(5.1)

Analizom navedene formule može se utvrditi da će vjerojatnost zamjene operatora biti u slučaju da nijedna mutacija nije bila uspješna, a u slučaju da su sve obavljene mutacije bile uspješne. Slika 5.5. prikazuje oblik funkcije vjerojatnosti promjene operatora mutacije u ovisnosti o omjeru uspješnosti mutacija.

Slika 5.5. Ovisnost vjerojatnosti promjene operatora o omjeru uspješnih mutacija

Statistika operatora mutacije (mutation operator statistics). Ovaj mehanizam prati uspješnost svakog pojedinog operatora na listi operatora mutacija, koristeći sve operatore istovremeno na način da o operatoru mutacije koji će se koristiti odlučuje neposredno prije obavljanja mutacije i to na temelju njegove uspješnosti naspram uspješnosti ostalih operatora. Konkretno, svakom od operatora pridjeljuje neku vjerojatnost da on bude odabran, te je na početku ta vjerojatnost jednaka za sve operatore. Potom, po isteku perioda adaptacije, ova metoda računa omjer uspješnosti mutacija svakom od operatora, te mu dodaje slučajnu vrijednost prema formuli (5.2).

(5.2)

Potom svakom od operatora dodjeljuje vjerojatnost da bude izabran prema formuli (5.3).

(5.3)

Razlog korištenja slučajne vrijednosti je da se izbjegne da neki od operatora trajno dobije vjerojatnost odabira . U tom slučaju bi se uzelo da mu je i omjer uspješnosti također jednak nuli, pa operator više ne bi imao prilike da bude ponovno korišten kasnije tijekom pretrage, kad bi opet mogao postati koristan.

Migracije populacija (population migrations). Naposljetku, migracije populacija je adaptivna metoda koja radi nešto drugačije od ostalih dosad opisanih. Ona radi na način da evoluira odvojene populacije jedinki, koristeći u svakoj samo jedan od unaprijed definiranih operatora mutacije. Nakon isteka perioda adaptacije, unaprijed definirani broj slučajnih jedinki se odabire iz svake od populacije, stavlja u bazen za migraciju (migration pool), te se sve te jedinke slučajnim odabirom raspoređuje između populacija. Nažalost, ova se metoda pokazalo prilično lošom, budući da dovodi do preuranjene konvergencije. Naime, čim se neko visokokvalitetno rješenje iz neke populacije nađe u nekoj manje kvalitetnoj populaciji, takvo rješenje brzo preuzme čitavu populaciju.

5.2. Eksperimentalni rezultati

U ovom su odjeljku prikazani dobiveni eksperimentalni rezultati. Također je pokazano da opisani mehanizmi adaptacije parametara pospješuju rad genetskog algoritma.

5.2.1. Skupovi parametara za mjerenja

Mjerenja su obavljena nad četiri vrste problema – kroA100, kroA200, Spiral250 i Multicircular500. Korištena je troturnirsku eliminaciju, operator križanja je bilo križanje u poretku, a početni operator mutacije bila je mutacija obrtanjem. Vjerojatnost mutacije postavljena je na , a period adaptacije iznosio je . Tablica 4.1. prikazuje vrijednosti ostalih parametara, koje su se mijenjale od problema do problema.

Tablica 5.1 Korištene vrijednosti parametara za pojedine probleme

Naziv problema	Veličina populacije	Broj iteracija	Korišteni operatori mutacije	Broj mjerenja
kroA100	100	200k, 500k, 1000k, 1500k	Posmak, obrtanje	20
kroA200	100	400k, 1000k, 2000k	Posmak, obrtanje	20
Spiral250	100	200k, 500k, 1000k, 1500k	Posmak, obrtanje, zamjena segmenata	20
Multicircular500	50	400k, 1000k, 2000k	Posmak, obrtanje	10

5.2.2. Rezultati i komentar

Kod svih je inačica problema mjerena dobivena cijena u ovisnosti o broju obavljenih iteracija algoritma. Iz dobivenih ovisnosti jasno se moglo analizirati uspješnost pojedinih adaptivnih metoda, te ih usporediti s neadaptivnom inačicom algoritma.

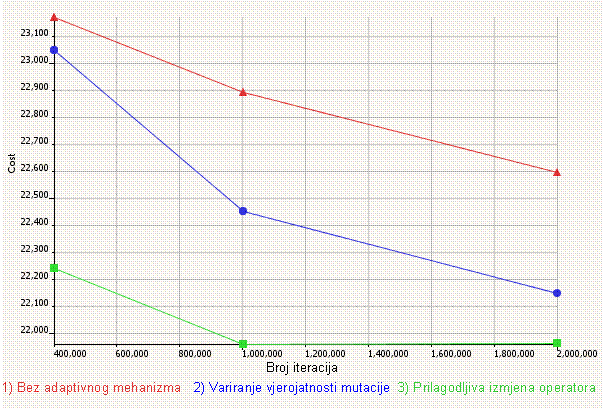
Slika 5.6. Ovisnost cijene najboljeg obilaska o broju iteracija za kroA100

Slika 5.6. prikazuje navedenu ovisnost za problem kroA100. Uspješnost metode prilagodljive izmjene operatora je ovdje očita – već nakon iteracija ova metoda svojom djelotvornošću nadilazi variranje vjerojatnosti mutacije, kao i neadaptivnu inačicu algoritma. Slika 5.7. prikazuje istu ovisnost za problem kroA200, kod kojeg se nakon iteracija prilagodljiva izmjena operatora nije iskazala kao prije, međutim, nakon iteracija, razlika je itekako vidljiva. Kod ove inačice problema variranje vjerojatnosti mutacije nije dalo dobre rezultate, te se pokazalo lošijim od neadaptivne inačice algoritma.

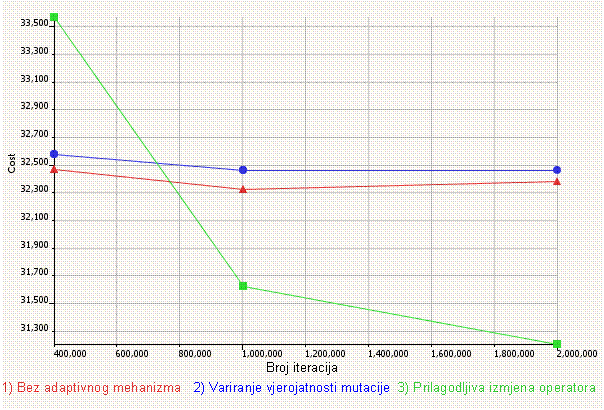
Slika 5.7. Ovisnost cijene najboljeg obilaska o broju iteracija za kroA200

Slika 5.8. prikazuje ovisnost cijene o broju iteracija za Spiral250. Radi preglednosti, dana su dva grafa, te je na jednom moguće usporediti rad variranja vjerojatnosti mutacije, prilagodljive izmjene operatora i neadaptivne inačice, dok je na drugom moguće usporediti statistiku operatora, migraciju populacija i neadaptivnu inačicu. Može se zamijetiti da iako sve adaptivne metode za najveći korišteni broj iteracija kod ove inačice problema nadmašuju običnu neadaptivnu inačicu algoritma, statistika operatora i migracija populacija ne nadmašuju neadaptivnu inačicu kroz dobar dio pretrage. Naime, sve opisane adaptivne metode imaju veću vjerojatnost bijega iz lokalnih optimuma koji se javljaju pri kraju pretrage kad je populacija dobrim dijelom već izkonvergirala, što objašnjava veći uspjeh adaptivnih metoda nakon većeg broja iteracija. Međutim, u početku pretrage kad se još nije naišlo na lokalne optimume, opisani mehanizmi samo usporavaju pretragu. Korištenje više od jedne vrste operatora mutacije umjesto jednog koji najbrže vodi do rješenja je dobar primjer za to.

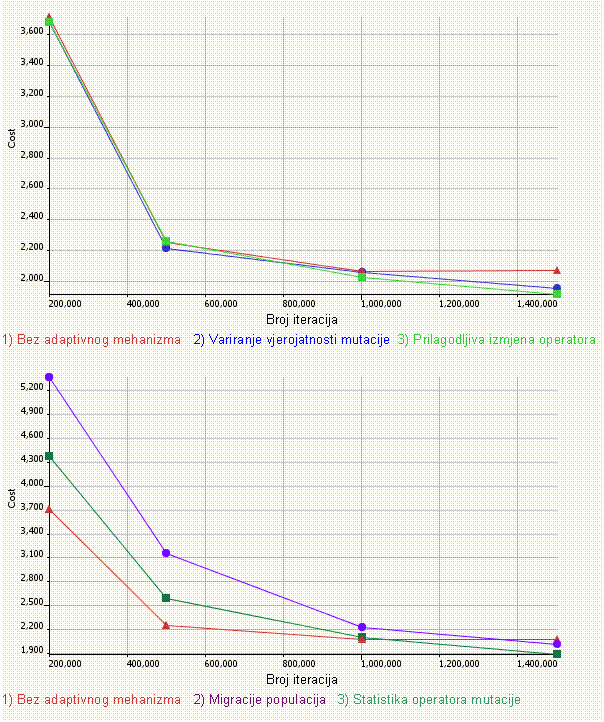
Slika 5.8. Ovisnost cijene najboljeg obilaska o broju iteracija za Spiral250

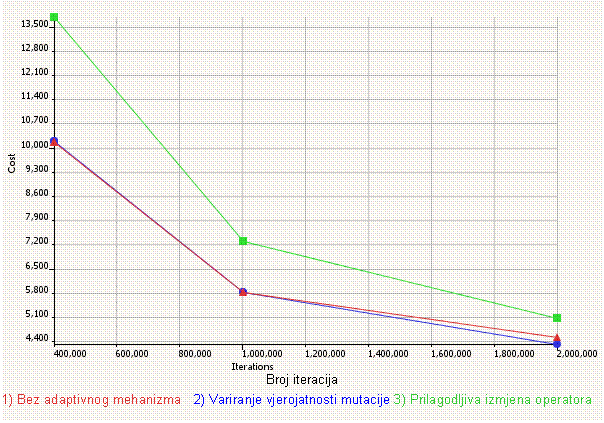
Slika 5.9. Ovisnost cijene najboljeg obilaska o broju iteracija za Multicircular500

Kod problema Multicircular500 većina se adaptivnih mehanizama pokazala manje uspješnom. Tek za 4·10⁶ iteracija je adaptivna izmjena operatora mutacije nadmašila neadaptivnu inačicu algoritma. Slika 5.9. prikazuje ovisnost cijene o broju iteracije, te se na njoj jasno vidi da prilagodljiva izmjena operatora daje lošije rezultate. Uz iste argumente kao i kod problema Spiral250, variranje vjerojatnosti mutacije pri kraju pretrage daje bolje rezultate od neadaptivne inačice, budući da povećana vjerojatnost mutacije daje bolje izglede za bijeg iz lokalnih optimuma.

Iz navedenih eksperimenata može se zaključiti da opisane adaptivne metode nisu u jednakoj mjeri uspješne za sve inačice problema. Nadalje, prava kombinacija operatora mutacije je nešto što također ovisi o inačici problema. Kao dobar tandem operatora mutacije za većinu primjera pokazali su se posmak i obrtanje.

6. Zaključak

U okviru ovog znanstveno-istraživačkog rada proučen je niz operatora za permutacijske probleme i nađen optimalni skup parametara za genetski algoritam koji rješava problem trgovačkog putnika. Razvijeno je više novih operatora mutacije, od kojih valja spomenuti operator posmaka i 2-opt operator. 2-opt operator se temelji na 2-opt heuristici i specifičan je za problem trgovačkog putnika, pa kao takav uvelike poboljšava svojstva genetskog algoritma. Time je pokazano da operatori koji u radu koriste znanje iz domene problema rade bolje od onih koji su osmišljeni za širu klasu permutacijskih problema. Operator posmaka nije djelotvoran poput mutacije obrtanjem, no genetski algoritam s njime radi bolje nego s mutacijom zamjene, mutacijom premetanjem i mutacijom ubacivanjem. Ipak, njegova se uloga očituje u kombinaciji s drugim operatorima, kao što su mutacija obrtanjem i 2-opt operator. Korištene adaptivne metode koje kombiniraju više operatora mutacije oslanjaju se na operator posmaka, i od svih poznatih operatora, čini se da najbolje rade upravo uz njega.

Korištene adaptivne metode oslanjaju se na mjerenje djelotvornosti pojedinih operatora mutacije i na detekciju pojave lokalnog optimuma. Variranje vjerojatnosti mutacije i prilagodljiva izmjena operatora oslanjaju se na detekciju pojave lokalnog optimuma, a prilagodljiva izmjena operatora s većom vjerojatnošću zamjenjuje operator čija je djelotvornost manja. Statistika operatora mutacije se također oslanja na djelotvornost pojedinog operatora mutacije, dajući prednost operatorima s većim brojem uspješnih mutacija.

Uveden je pojam krajolika funkcije prikladnosti za permutacijske probleme, pojam susjedstva za permutacije i pojam lokalnog optimuma. Pokazujući da se svi ti pojmovi temelje na korištenom operatoru mutacije, ponuđeno je teoretsko objašnjenje zašto bi pravovremena promjena operatora mutacije mogla imati pozitivan učinak na rad genetskog algoritma.

Naposljetku, eksperimentalni rezultati bili su pozitivni – adaptivne metode koje se temelje na promjeni operatora mutacije, ili na korištenju većeg broja istih ubrzale su rad genetskog algoritma i povećale vjerojatnost bijega iz lokalnog optimuma. U slučaju većeg broja gradova (iznad 500), adaptivni mehanizmi su se pokazali manje djelotvornima. Bio je potreban veći broj iteracija kako bi nadmašili neadaptivnu inačicu algoritma.

Ovaj rad otvara i čitav niz pitanja. Prije svega, 2-opt operator bi trebalo usporediti sa sličnim operatorom kojeg predlažu Sengoku i Yoshihara [29], te zaključiti o tome koji je djelotvorniji. Također, trebalo bi istražiti nove operatore mutacije i odrediti one koji dobro rade zajedno.

7. Literatura

[1] G. Eiben, J. Smith 2003. Introduction to Evolutionary Computing

[1] D. Ashlock 2005. Evolutionary Computation for Modelling and Optimization

[2] X. Yao, Y. Liu 1997. Fast Evolution Strategies

[3] A. E. Eiben, R. Hinterding, Z. Michalewicz 1999. Parameter Control In Evolutionary Algorithms

[4] K. Chellapilla, D. B. Fogel 2001. Evolving an Expert Checkers Player Without Using Human Expertise

[5] A. E. Eiben, Zs. Ruttkay 1996. Self-Adaptivity for Constraint Satisfaction: Learning Penalty Functions

[6] J. A. Joines, C. R. Houck 1994. On the Use of Non-Stationary Penalty Functions to Solve Nonlinear Constrained Optimization Problems with GA’s

[7] Z. Michalewicz, N. F. Attia 1994. Evolutionary Optimization of Constrained Problems

[8] J. C. Bean, A. B. Hadj-Alouane 1993. A Dual Genetic Algorithm for Bounded Integer Programs

[9] A. E. Eiben, J. K. van der Hauw 1997. Adaptive Penalties for Evolutionary Graph Coloring

[10] S. Yang 2002. Adaptive Crossover in Genetic Algorithms Using Statistics Mechanism

[11] A. E. Eiben, I. G. S.-Kuyper, B. A. Thijssen 1997. Competing Crossovers in an Adaptive GA Framework

[12] S. J. Louis, G. J. E. Rawlins 1991. Designer Genetic Algorithms: Genetic Algorithms in Structure Design

[13] K. Vekaria, C. Clack 1998. Selective Crossover in Genetic Algorithms: An Empirical Study

[14] K. Vekaria, C. Clack 1999. Biases Introduced by Adaptive Recombination Operators

[15] W. M. Spears 1995. Adapting Crossover in Evolutionary Algorithms

[16] J. E. Smith, T. C. Fogarty 1995. An Adaptive Poly-Parental Recombination Strategy

[17] J. E. Smith, T. C. Fogarty 1996. Adaptively Parametrised Evolutionary Systems: Self-Adaptive Recombination and Mutation in a Genetic Algorithm

[18] T. Bäck, D. B. Fogel, Z. Michalewicz 2000. Evolutionary Computation I

[19] D. Thierens 2002. Adaptive Mutation Rate Control Schemes in Genetic Algorithms

[20] D. Jakobović 1998. Adaptive Genetic Operators in Elimination Genetic Algorithm

[21] D. Jakobović, M. Golub 1999. Adaptive Genetic Algorithm

[22] T. P. Runarsson, X. Yao 2000. Stochastic Ranking for Constrained Evolutionary Optimization

[23] P. D. Surry, N. J. Radcliffe 1997. The COMOGA method: Constrained Optimisation by Multi-Objective Genetic Algorithms

[24] F. G. Lobo, C. F. Lima 2005. A Review of Adaptive Population Sizing Schemes in Genetic Algorithms

[25] J. Arabas, Z. Michalewicz, J. Mulawka 1994. GAVaPS – a Genetic Algorithm with Varying Population Size

[26] D. S.-Voosen, H. Mühlenbein 1994. Strategy Adaptation by Competing Subpopulations

[27] K. A. De Jong, W. M. Spears 1989. Using Genetic Algorithms to Solve NP-Complete Problems

[28] H. Sengoku, I. Yoshihara 1998. A Fast TSP Solver Using GA on JAVA

[29] H. Mauch 2004. Closest Substring Problem – Results from an Evolutionary Algorithm

[30] G. Laporte 2006. A Short History of the Traveling Salesman Problem

[31] G. Gutin, A. Yeo, A. Zverovich 2002. Traveling Salesman Should Not Be Greedy: Domination Analysis of Greedy-type Heuristics for the TSP

[32] The Traveling Salesman Problem (http://www.tsp.gatech.edu/index.html)

[1] Vrijednost iz skupa u kojem postoji poredak

[4] Distribucija kod koje je vjerojatnost pojave svake od vrijednosti jednaka.

[5] Vidi No Free Lunch teorem. Navedeni teorem zbog svog opsega nije razmatran u okviru ovog rada.

[6] Ovdje se ne misli na generaciju u radu genetskog algoritma, već na jedan poziv čitavog genetskog algoritma.

[7] Naziv je posuđen iz terminologije simuliranog kaljenja (simulated annealing), odakle autori i vuku inspiraciju za Genocop II.

[8] Izraz lošija označava veću vrijednost u slučaju minimizacijskih problema, a manju u slučaju maksimizacijskih problema.

[9] Yang pretpostavlja bitovni prikaz. Moguće poopćenje moglo bi se sastojati od traženja srednje vrijednosti alele u populaciji, te određivanju parametra za aritmetičku rekombinaciju na temelju udaljenosti od srednje vrijednosti.

[10] Misli se na povlačenje nasumične vrijednosti iz intervala [0, 1] gdje je prag za odluku 0.5.

[11] Jednostavni put (simple path) je niz vrhova u grafu takav da se nijedan vrh ne ponavlja