2.2 Algoritmi putanje
Algoritmi putanje su oni metaheuristički algoritmi koji u svakom koraku izabiru samo jedno (trenutno) rješenje. Ime su dobili po tome što se ovakvim načinom opisuje putanja u prostoru pretrage rješenja. Algoritmi putanje opisani u ovom podpoglavlju su: pohlepni algoritam, lokalno pretraživanje, algoritam simuliranog kaljenja, tabu pretraživanje i pretraživanje promjenjivom okolinom.
2.2.1 Pohlepni algoriatm
Jedan od najjednostavnijih heurističkih algoritama je pohlepni algoritam (Greedy Algorithm). Traženje optimalnog rješenja može biti eksponencijalne složenosti, a pohlepni algoritam smanjujući prostor pretraživanja, smanjuje i samu složenost. Naime, pohlepni pristup nas u svakom trenutku usmjeruje na trenutno najbolje rješenje, ne uzimajući u obzir da nas to ne mora voditi k globalnom optimumu. Zbog toga, pohlepni algoritam ne mora uvijek naći optimalno rješenje, ali je znatno brži od drugih algoritama.
Primjer 2.1.
Trgovac koji koristi pohlepni algoritam
Tipičan primjer na kojem se ilustrira pohlepni algoritam (zasnovan na pohlepnom pristupu) je povrat ostatka (novca) prilikom kupnje. Kupac je platio neki proizvod s novčanicom većom nego je proizvod koštao i sada mu trgovac treba vratiti određenu sumu novca S. Neka trgovac pri tome ima kod sebe puno novčanica N1, N2, N3 i N4 (N1>N2>N3>N4=1) i neka može odjednom staviti u ruke kupcu samo jednu novčanicu. Trgovcu se žuri (jer je red u trgovini jako velik) i u interesu mu je što prije vratiti ostatak kupcu. Budući da je trgovac obrazovan, on zna za pohlepni algoritam i koristi ga. Trgovac čini:
1. stavlja najveću novčanicu koja ne prelazi sumu S
2. od sume S oduzima vrijednost te novčanice i suma S poprima vrijednost dobivene razlike
3. ako je S jednako nula trgovac je vratio ostatak, inače se vraća na korak 1.
Izračunaj
ostatak S koji treba vratiti;
Dok
(N1 <= S) {
Stavi
novčanicu N1 u ruke kupcu;
S
= S - N1;
}
Dok
(N2 <= S) {
Stavi
novčanicu N2 u ruke kupcu;
S
= S - N2;
}
Dok
(N3 <= S) {
Stavi
novčanicu N3 u ruke kupcu;
S
= S - N3;
}
Dok
(N4 <= S) {
Stavi
novčanicu N4 u ruke kupcu;
S
= S - N4;
}
Obavi
ostale poslove;
Slika 2.2 Pseudokod trgovca
Ako trgovac treba vratiti 62 kn, a posjeduje novčanice od 50 kn, 10 kn, 5 kn i 1 kn, trgovac će vratiti ostatak sa jednom novčanicom od 50 kn, jednom od 10 kn i dvije novčanice od 1 kn. Ovakav pristup ne mora nužno voditi do najboljeg rješenja. Ako trgovac, primjerice, treba vratiti 15 kn, a ima novčanice od 11 kn, 5 kn i 1 kn, on će pohlepnim algoritmom vratiti ostatak jednom novčanicom od 11 kn i četiri novčanice od 1 kn, premda bi mu bilo brže vratiti ostatak sa tri novčanice od 5 kn.
Premda pohlepni
algoritam ne mora uvijek voditi globalnom optimumu, on može biti vrlo
koristan
u razmatranju NP-teških problema. Naime, pohlepni pristup
vodi do rješenja koje
sigurno predstavlja donju među (ogradu) globalnog maksimuma, ukoliko se
traži maksimum, odnosno gornju među globalnog minimuma, ukoliko se
traži
minimum. Kako se pohlepni algoritam brzo izvodi i daje ogradu
optimalnom
rješenju, on nam omogućava da drugim algoritmima smanjimo
prostor pretrage
rješenja.
Dodatna prednost pohlepne
strategije je da, čak i kada ne pronađe optimalno rješenje,
često vodi na novu strategiju razvoja algoritma koja rezultira
efikasnijim
rješenjem ili tehnikom koja brzo pronalazi dobru
aproksimaciju rješenja
(heuristika) [6]. Heuristika koju koristi pohlepni algoritam je
jednostavna:
pronađi najbolje trenutno rješenje i idi za njim. Valja
napomenuti da
postoje mnogi algoritmi koji su zasnovani na pohlepnom pristupu, pa
kada
govorimo o pohlepnom algoritmu, ustvari govorimo o skupini algoritama.
Postoje
problemi kod kojih je dokazano da pohlepni
algoritam daje optimalno rješenje. Jedan od tih problema je
i problem rasporeda
zadataka. Pitanje je kako rasporediti zadatke, a da prosječno vrijeme
završavanja zadatka bude minimalno. Neka su poslovi a1, a2,
a3 i a4, a njihova
vremena izvođenja redom dta1=10s, dta2=11s, dta3=5s i dta4=15s. Ako
poredamo
poslove redoslijedom a1, a2, a3 i a4 onda će vrijeme
završavanja poslova
(od početnog trenutka) biti redom t1=10s, t2=21s, t3=26s i t4=41s.
Prosječno vrijeme završavanja (od početnog trenutka) jednako
je
tp=24.5s. Sada preuredimo raspored tako da prvi poslovi budu oni s
manjim
vremenima trajanja, tj. da se poslovi obavljaju redom a3, a1, a2 i a4.
To je u
skladu s pohlepnim pristupom. Vremena završavanja će
iznositi redom t3=5s,
t1=15s, t2= 26s i t4=41, a prosječno vrijeme izvršavanja će
biti
tp=21.75s. Općenito se može dokazati da će prosječno vrijeme
završavanja biti najmanje ako najprije obavljamo najkraće
poslove (u
skladu s pohlepnim algoritmom). Ipak, valja pripaziti kada ovom
problemu
pristupamo pohlepnim algoritmom jer nemaju svi poslovi jednak prioritet
[3, 6,
7, 9].
2.2.2 Lokalno pretraživanje
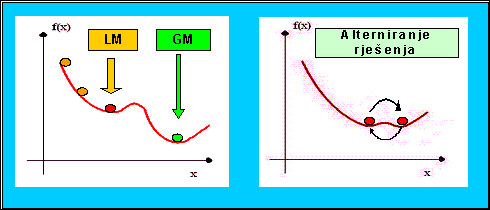
Kao i svi heuristički algoritmi, tako i lokalno pretraživanje (Local Search, LS) nastoji pronaći optimalno rješenje zadanog problema smanjujući prostor pretraživanja. LS možemo opisati u nekoliko koraka. Prvo se odabere rješenje i izmjeri se njegova vrijednost (ili valjanost; ovisno o problemu koji se promatra). Zatim se pretražuju susjedi od odabranog rješenja i u ovisnosti o njihovim vrijednostima se izabere najbolji. Susjedi su pri tome definirani ovisno o problemu koji se promatra. Sada se nizom iteracija nastoji doći do optimalnog rješenja. Trajanje algoritma je određeno brojem iteracija, bez obzira je li pronađeno rješenje, pa ga svrstavamo u nezavršne algoritme, kao i većinu metaheurističkih algoritama. Bitno je uočiti da algoritam zamjene sa najboljim susjedom može dovesti do neprestanog alterniranja dvaju susjeda u izboru rješenja, pa algoritam neće postići stabilizaciju u globalnom optimumu. Taj problem je moguće riješiti odabirom dobre funkcije cilja (funkcije transformacije trenutnog rješenja), tj. odabirom dovoljno velikog lokalnog prostora pretraživanja (odabirom dovoljno velikog broja susjeda ukoliko je moguće), ili malom preinakom algoritma. Dakako, ukoliko se podešava lokalni prostor pretrage, treba paziti da ne bude prevelik jer se može dogoditi da nam je odabir susjeda sveden na odabir slučajne varijable unutar prostora mogućih rješenja.
.
Primjer
2.2 Lokalno pretraživanje na
problemu SAT
Ilustrirajmo algoritam lokalnog pretraživanja na prvom problemu za kojeg je pokazano da je NP-potpun. To je problem zadovoljenja Booleove formule, a češće se označava sa SAT ( SAT(x) znači „x je propozicijska formula koja je istinita za neke Booleove vrijednosti”[10]). Potrebno je otkriti postoji li kombinacija vrijednosti varijabli (istina ili laž) da Booleova formula bude istinita. SAT spada u klasu NP-potpunih problema. Pogodno je Booleovu funkciju napisati u potpunom konjuktivnom obliku (produktu makstermi), te argumentima (varijablama) funkcije pridružiti binarni vektor. Taj vektor će predstavljati vrijednost argumenata funkcije (0-laž, 1-istina). Problem ćemo riješiti GSAT algoritmom. GSAT algoritam se sastoji od dvije petlje, jedna ugniježđena u drugoj. U prvoj petlji se nasumice odabire jedan binarni vektor, a sama petlja ima konačno mnogo iteracija. Druga petlja je ugniježđena u prvu i kroz konačno mnogo iteracija provjerava da li za binarni vektor
funkcija GSAT (funkcija *Booleova){
binarni_vektor t;
indeks p;
za (i = 1 do BROJ_POKUŠAJA) {
t=slučajno_odaberi();
za (j = 1 do BROJ_PROMJENA){
ako (Booleova(t)==istina) vrati t;
odredi indeks bita p čijom promjenom dobivamo
najveći broj istinitih makstermi;
t(p)=1-t(p);
}
}
vrati nisam našao zadovoljavajući vektor
}
Slika 2.4 Pseudokod GSAT-a
(određene vrijednosti literala) Booleova funkcija poprima vrijednost istine. Ako poprima, algoritam završava sa izvođenjem, a ako ne, mijenja se jedan od bitova binarnog vektora (vrijednost jednog literala) i to onaj čijom promjenom najveći broj makstermi poprima vrijednost istine. Pri tome se može i smanjiti broj istinitih makstermi. Algoritam završava pronalaženjem binarnog vektora za kojeg Booleov izraz poprima vrijednost istina ili prolaskom kroz obje petlje.
Da bi izbjegli pojavu zaglavljivanja u lokalnom optimumu, možemo za svaku makstermu uvesti oznaku težine koja će se povećavati unutar ugniježđene petlje dok god maksterma nema vrijednost istine za binarni vektor t [5]. Sada će se mijenjati onaj bit binarnog vektora t čijom je promjenom zbroj težina neistinitih makstermi najmanji [5, 10].
...
težine
mintermi w[2^broj_varijabli]={0};
...
ako
(Booleova(t)==istina) vrati t;
odredi indeks bita p čijom promjenom zbroj težina
neistinitih makstermi za bitovni vektor t je najmanji i uvećaj težine tih makstermi;
t(p)=1-t(p);
...
Slika 2.5 Poboljšani GSAT
2.2.3 Algoritam simuliranog kaljenja
Algoritam simuliranog kaljenja (Simulated Annealing, SA) jedan je od stohastičkih optimizacijskih algoritama, a razlikuje se od algoritama lokalnog pretraživanja po tome što omogućuje bijeg iz lokalnog optimuma. Algoritam je nastao po analogiji sa metalurškim kaljenjem, čiji je cilj oplemenjivanje metala tako da oni postanu čvršći. Ako želimo postići čvrstoću metala, potrebno je kristalnu rešetku metala pomjeriti tako da ima minimalnu potencijalnu energiju. U procesu metalurškog kaljenja metal se prvo zagrijava do visoke temperature, a potom se, nakon kraćeg zadržavanja na toj temperaturi, polagano hladi do sobne temperature. Prebrzo hlađenje bi moglo uzrokovati pucanje metala. Posljedica toga je da atomi metala nakon procesa kaljenja tvore pravilnu kristalnu rešetku. Time je postignut i energetski minimum kristalne rešetke.
U skladu s navedenim, SA će sadržavati parametar temperature, a funkciju kojoj želimo odrediti globalni optimum možemo promatrati kao energiju rešetke, ukoliko određujemo minimum, odnosno negativnu energiju rešetke, ukoliko određujemo maksimum. Algoritam počinje odabirom nekog početnog rješenja, a početna temperatura ima relativno veliku vrijednost. Postojeće rješenje se zamjenjuje sa boljim, ali se može zamijeniti i sa lošijim uz određenu vjerojatnost prihvaćanja [12]. Ta vjerojatnost se određuje odabirom slučajnog broja a iz intervala [0,1] i uvjeta da je a manje od exp(E(staro) – E(novo)/T), gdje je E(x) funkcija za koju se traži globalni minimum, a T temperatura. Ukoliko je izraz istinit novo rješenje se prihvaća. Ovo nam omogućava bijeg iz lokalnog minimuma. Isto tako, vjerojatnost da će biti odabrano lošije rješenje je veće kada je veća temperatura. To znači da je u početku prostor pretrage rješenja dosta velik i da se smanjuje padom temperature, a pri kraju procesa je usko lokaliziran. Ponašanje funkcije je uvelike određeno početnom vrijednosti temperature i njenom brzinom padanja. Najčešće temperatura opada eksponencijalno s parametrom a iz intervala 0<a<1 (a je blizak jedinici). Za premali a hlađenje je prebrzo (pucanje metala) i veća je vjerojatnost upada u lokalni optimum. Za preveliki a temperatura presporo pada, i zbog velike vjerojatnosti da se u početku zamjenjuju bolja rješenja s lošijim, algoritam ima svojstvo da nasumično pretražuje veliki prostor rješenja. To dodatno usporava rad, te se a nastoji odabrati da bude dovoljno velik, ali da temperatura pri kraju procesa bude niska. Time se rješenje pred kraj procesa stabilizira u lokalnom području. Zbog velike osjetljivosti na koeficijent a, posebnu pažnju valja obratiti njegovom odabiranju.
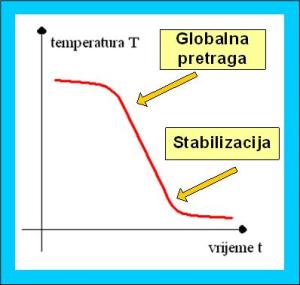
Slika 2.6 Globalna pretraga i stabilizacija kod SA-a
Primjer
2.3 Problem naprtnjače i SA
SA se može dobro opisati na problemu naprtnjače. Zamislimo vozača kamiona Matu koji ima osmeročlanu obitelj i koji svojim kamionom prevozi raznovrsnu robu zarađujući tako za život. Pitanje se postavlja kako će Mate najviše profitirati ako se zna da su svi predmeti različiti, svaki predmet ima određen profit i masu, te da njegov kamion ima ograničenu nosivost N. Mate zna za algoritam simuliranog kaljena, te pokušava konstruirati najbolje rješenje. On uzima polje nula i jedinica (polje x), koje mu označava koji će element uzeti, i dva polja od n elemenata: jedno da stavi profite pojedinih predmeta (polje p), a drugo da stavi mase pojedinih predmeta (polje t). Ovisno o vremenskim prilikama, on odabire početnu temperaturu i koeficijent a. Ukupni profit odabranih predmeta P i ukupna masa odabranih predmeta M se dobivaju po formulama (2.1).
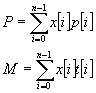
(2.1)
Pri odabiru polja x, Mate pazi da ukupna masa (M) nije veća od nosivosti (N), pa uzima u obzir samo rješenja koja zadovoljavaju taj uvjet. Isto tako, on je uočio da je zgodno imati varijablu koja pamti najbolju kombinaciju predmeta uopće (xnaj, Pmax). Naime, trenutno rješenje se nastoji „poboljšati”, ali moguće je i „pogoršanje”, pa on ovako dobiva najbolje rješenje od onih kombinacija koje je pregledao [11, 12].
funkcija
simuliranog_kaljenja(nosivost N, poc_temp T0, koef_alfa a){
temperatura
T=T0;
polje_odabira
x={0},y,xnaj={0};
polje_profita
p;
profit
Pmax=0,Ptr=0;
polje_masa
t;
ukupna_masa
M=0;
slucajna
v,r;
dopustivo
d;
za(i=0;
i<broj_iteracija; i++){
v =
slucajno_odaberi_iz_intervala_(0,n-1);
y=x;
y[v]=1-x[v];
ako(y[v]==1 i (M+t[v] > N)) d=laž;
inače d=istina;
ako(d==istina){
//zamjena s boljim
rješenjem
ako(y[v]==1){
x=y;
M+=t[v];
Ptr+=p[i]*x[i];
ako(Ptr
> Pmax) {
xnaj=x;
Pmax=Ptr;
}
}
//zamjena s gorim rješenjem
inače{
r=
slucajno_odaberi_iz_intervala_(0,1);
ako(r <
exp(-p[v]/T)){
x=y;
M-=t[v];
}
}
}
T=a*T;
}
vrati
xnaj;
}
Slika 2.7 Pseudokod SA-a za
problem naprtnjače
2.2.4 Tabu pretraživanje
Tabu pretraživanje (Tabu Search, TS) kombinira osnovni algoritam lokalnog pretraživanja sa kratkotrajnom memorijom koja mu omogućuje bijeg iz lokalnog optimuma i izbjegavanje alternacije dvaju rješenja[1]. Cilj je odrediti optimum zadane funkcije. U tu svrhu, algoritam koristi posebnu tabu listu koja služi kao kratkotrajna memorija. U njoj pamti rješenja odabrana unatrag nekoliko prethodnih koraka. Rješenja koja se nalaze u tabu listi se ne mogu pojaviti kao rješenje u sljedećem koraku. Time je definiran dopušteni skup rješenja u sljedećem koraku. Ponašanje algoritma ovisi o veličini tabu liste i veličina se podešava tako da ne bude premala, jer to može dovesti do cikličkog ponavljanja rješenja, niti prevelika, jer to može dovesti do znatnog usporenja algoritma. Kada se odredi novo rješenje, iz tabu liste se po principu FIFO (first in, first out) strukture izbacuje jedno rješenje i stavlja novo. Algoritam se obavlja dok god se ne zadovolji kriterij zaustavljanja ili se svako moguće rješenje nalazi u tabu listi. Ovako jednostavno definiran algoritam moguće je unaprijediti. Umjesto da se stavljaju rješenja u tabu listu, što često nije učinkovito zbog mogućeg zapisa rješenja, mogu se u tabu listu staviti samo atributi koji opisuju rješenje. Time se gube neke informacije o rješenju (jer različita rješenja mogu imati iste atribute), ali se dobiva na brzini i jednostavnosti pretrage i korištenja tabu liste.
Inicijaliziraj
tabu_lista;
Inicijaliziraj
x; //početno rješenje
Skup_rješenja
X=Ø;
Dok
(Zaustavni_kriterij != zadovoljen){
X={y|y
nije u tabu_lista ili
usisni_kriterij(y)==zadovoljen};
Ako(X
== Ø) izađi_iz_petlje;
x=odaberi_najbolji(X);
obnovi_tabu_listu();
obnovi_usisni_kriterij();
}
Slika 2.8 Pseudokod TS-a
Opis rješenja atributima može dovesti i do toga da se u sljedećim koracima ne mogu pojaviti rješenja koja imaju isti opis kao i rješenje odabrano u nekom od prethodnih koraka, a to može uzrokovati ispuštanjem dobrih rješenja. Da bi se to izbjeglo, uvodi se usisni kriterij koji omogućava da se rješenje pojavi premda ga tabu lista zabranjuje. Najčešće je usisni kriterij tako postavljen da se usisavaju ona rješenja koja su bolja od trenutno najboljeg.
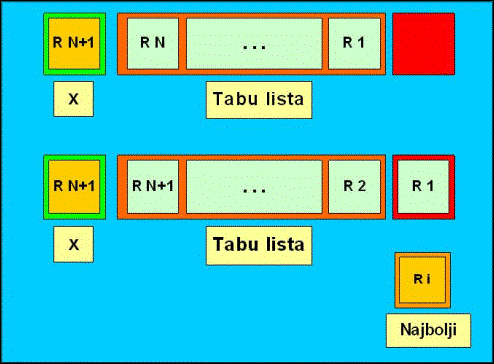
Slika 2.9 Ubacivanje u tabu
listu
Osim kratkotrajne memorije, algoritam može koristiti i dugotrajnu memoriju koja posjeduje informacije od početka djelovanja algoritma. Ona može koristiti algoritmu kao strateška potpora, a uglavnom je zasnovana na jednom od četiri principa: svježine, učestalosti, kvalitete i utjecaja [1]. Memorija zasnovana na principu svježine nam daje za svako rješenje (ili atribut) najbližu iteraciju u kojem je rješenje odabrano, dok nam memorija zasnovana na principu učestalosti daje za svako rješenje (ili atribut) broj njegova odabira. Memorija zasnovana na principu kvalitete nam omogućava da razlučimo potencijalno dobra rješenja od loših, a memorija zasnovana na principu utjecaja nam daje informacije o najkritičnijim odlukama.
Ovako definiran algoritam se vrlo lako može izmijeniti ili nadopuniti u cilju poboljšanja njegovih karakteristika, a dokaz tomu su i unaprijeđene varijante tabu pretraživanja poput robusnog tabu pretraživanja ili reaktivnog tabu pretraživanja [1, 2].
2.2.5 Pretraživanje promjenjivom okolinom
Pretraživanja promjenjivom okolinom (Variable Neighborhood Search,VNS) je metaheuristički algoritam koji se zasniva na promjeni okoline (susjedstva) prilikom traženja optimalnog rješenja. Postoje različite inačice algoritma, a sve su međusobno slične. Za sve varijante je karakteristično da prvo izaberu konačan skup susjednih struktura Nk(k=1,...,n) i generiraju početno rješenje r, a međusobno se razlikuju u načinu korištenja susjednih struktura prilikom pretrage prostora rješenja. Skup susjednih struktura se tipično odabire tako da vrijedi |N1| <...<|Nk|. U nastavku će se opisati najpoznatije inačice, a opisivanje započinjemo sa osnovnim VNS-om.
Osnovni VNS (Basic VNS, BVNS), kao i druge inačice, prvo izabere skup susjednih struktura i generira početno rješenje. Tijelo algoritma je ostvareno dvjema petljama. Vanjska petlja čini ciklus koji se prekida kada je zadovoljen zaustavni kriterij. Ugniježđena petlja traži optimalno rješenje kroz n susjedstava i u njoj razabiremo tri
Izaberi
skup susjedstva N[n];
Brojilo
k=1,...,n;
r=generiraj_rješenje();
dok(zaustavni_kriterij
!= zadovoljen){
k=1;
dok(k <= n){
r2=slučano_odaberi(N[k]);
r3=lokalno_pretraživanje(N[1],r2);
//f je funkcija koja se minimizira
ako(f(r3) < f(r)){
r=r3;
k=1;
}
inače k++;
}
}
Slika 2.10 Pseudokod BVNS-a
dijela. U prvom dijelu se slučajno odabire rješenje iz k-tog susjedstva, gdje je k brojilo koje ovisi o broju iteracija petlje i valjanosti odabranih rješenja iz prethodnih susjedstava. Drugi dio predstavlja lokalno pretraživanje po nekom od susjedstava, pri
čemu početno rješenje predstavlja rješenje generirano iz prvog dijela petlje. Lokalno pretraživanje se uglavnom provodi nad prvim susjedstvom, a čak se može stvoriti posebno susjedstvo koje se ne nalazi u skupu izabranih susjedstava i nad njime vršiti lokalno pretraživanje. Rješenje koje dobijemo lokalnim pretraživanjem u trećem dijelu uspoređuje se s dosad najboljim rješenjem, i ukoliko je optimalnije, izabire se kao najbolje. U suprotnome se prelazi na potragu za najboljim rješenjem uz pomoć sljedećeg susjedstva (brojilo k se uvećava).
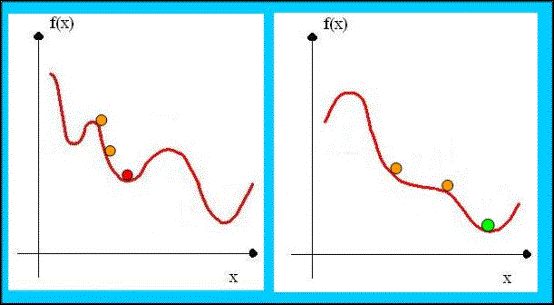
Slika 2.11 Pretraživanje po
različitim okolinama
Bitno je istaknuti da lokalni optimum u jednom susjedstvu ne znači nužno i lokalni optimum u drugom susjedstvu [13]. To nam unosi raznolikost u našu pretragu i donekle omogućava bijeg iz lokalnog optimuma. Bijeg iz lokalnog optimuma se zasniva na činjenici da dobro rješenje u jednom susjedstvu ne znači i dobro rješenje u drugom susjedstvu. To je posljedica različitih kardinalnosti susjedstava.
Umjesto da u k-tom koraku nasumično izabiremo rješenja iz k-tog susjedstva i provodimo lokalno pretraživanje nad samo jednim susjedstvom, možemo napraviti poboljšanje tako da pronađemo najboljeg susjeda od trenutnog rješenja u k-tom susjedstvu. Ova inačica algoritma se naziva spuštanje promjenjivom okolinom (Variable Neighborhood Descent, VND).
...
r2=pronađi_najboljeg_susjeda(N[k],r);
//f
je funkcija koja se minimizira
ako(f(r2)
< f(r)){
r=r3;
k=1;
}
inače
k++;
...
Slika 2.12 Pseudokod VND-a
U svrhu postizanja veće brzine, može nam poslužiti inačica algoritma poznata kao reducirano pretraživanje promjenjivom okolinom (Reduced VNS, RVNS). RVNS je isti kao i BVNS samo što nema lokalnog pretraživanja u svrhu poboljšanja slučajno izabranog rješenja iz susjedstva Nk. Vidimo da RVNS traži rješenje slučajno birajući rješenja iz različitih susjedstva. Činjenica da ne sadrži lokalno pretraživanje ga znatno ubrzava, ali je time dozvoljena veća učestalost pojave krivih rješenja.
Neka se rješenja traženog problema mogu rastaviti na komponente. Tada, u svakom koraku BVNS-a možemo svakom rješenju pridružiti točno k promjenjivih komponenti. Struktura susjedstva Nk izmijenjenog algoritma je jasno definirana, a prilikom lokalnom pretraživanja mijenjamo samo promjenjive komponente. Takva inačica algoritma se naziva dekompozicijsko pretraživanje promjenjive okoline (Variable Neighborhood Decomposition Search, VNDS).
...
r2=slučano_odaberi(N[k]);
r3=lokalno_pretraživanje(N[1],r2,prom_komponente);
//f
je funkcija koja se minimizira
ako(f(r3)
< f(r)){
r=r3;
k=1;
}
inače
k++;
...
Slika 2.13
Pseudokod
VNDS-a
BVNS ne omogućava zamjenu rješenja r sa lošijim rješenjem r3. Ponekad bi ta zamjena mogla brže voditi do boljeg rješenja i vjerojatnijeg bijega iz lokalnog optimuma. Prihvaćanje lošijeg rješenja bi trebalo ovisiti o udaljenosti δ(r,r3) između r i r3, te o parametru α koji predstavlja važnost udaljenosti u ispitnom kriteriju. Izmijenimo li BVNS u skladu sa prethodnim razmatranjem dobivamo algoritam ukošenog pretraživanja promjenjivom okolinom (Skewed VNS, SVNS).
...
ako(f(r3)+
a*d(r,r3)< f(r)){
r=r3;
k=1;
}
inače
k++;
...
Slika 2.14
Pseudokod
SVNS-a
VNS skupina algoritama uspješno rješava kombinatorne probleme vezane uz kombinatornu strukturu graf [1, 2, 13].