Kako nam evolucija može pomoći pri potrazi za rješenjem pretraživanja? Odgovor na ovo pitanje predložen je u sedamdesetim godinama u obliku genetskih algoritama. Genetski algoritmi su grupa algoritama koji koriste evolucijske procese kako bi pronašli najbolje rješenje. Osnovna ideja je da se ograničen broj rješenja bori za opstanak i rekombinaciju uz stalno stvaranje novih rješenja. Ova ideja provodi se po uzoru na evoluciju u prirodi pa se rješenja mijenjaju i unaprjeđuju kroz generacije.

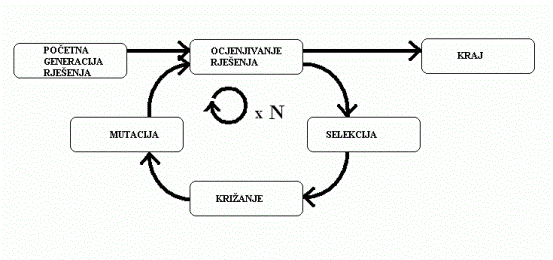
Slika 1.1 Shema genetskog algoritma

Na početku rada se odabere određen broj rješenja problema. Odabrana rješenja predstavljaju početnu generaciju rješenja i potom se poboljšavaju kroz niz generacija. U procesu rada algoritma rješenje se promatra kao jedinku. Pri stvaranju iduće generacije svaka se jedinka ocjenjuje i temeljem ocjena se biraju jedinke koje će se križati oponašajući tako prirodni proces reprodukcije. Neke jedinke prolaze i proces mutacije gdje se njihovi dijelovi nasumično mijenjaju kako bi se dobile jedinke s novim svojstvima koje roditelji nisu imali. Ponavljajući ovaj postupak kroz niz generacija dobivaju se sve bolja rješenja. Koliko će genetski algoritam i njegova rješenja biti dobri ovisi o načinu na koji su implementirani navedeni dijelovi.

Pojednostavljena svrha genetskog algoritma je pronalazak maksimuma određene funkcije uz zadane uvjete, primjerice traženje najviše geografske visine u određenom prostoru ili najniže cijene nekog procesa uz određene uvjete.

Genetski algoritmi predstavljaju alat za rješavanje optimizacijskih problema gdje je područje pretraživanja preveliko da bi se cijelo moglo istražiti. Rješavanje problema s par tisuća nepoznanica ili prostorno slaganje atoma primjeri su takvih pretraživanja. Kako neka od mogućih rješenja genetski algoritam ne provjeri slijedi da dobiveno rješenje ne mora nužno biti i najbolje moguće. U praktičnoj primjeni često nam nije važno dobiti najbolje, već dovoljno dobro rješenje, a tu su genetski algoritmi često uspješni.

Genetski algoritmi pri svom radu upotrebljavaju vrlo malo znanja koja su specifična za problem koji se rješava te mogu rješavati sve optimizacijske probleme pretraživanja, pa su oni općenit način pretraživanja. Specifična znanja za određeni problem izdvajaju se u funkciju u kojoj se ocjenjuje koliko je određeno rješenje dobro, ali se osnovni način potrage ne mijenja ovisno o parametrima problema. Zbog toga su ovi algoritmi dobar izbor kada treba pronalaziti rješenja uz promjenjive parametre, primjerice upravljanje robotom u promjenjivoj okolini [Mitchell, 1999]. Prednost ovakvog pristupa je što se najveći broj odluka pri rješavanju prepušta računalu: zadaju se uvjeti pretraživanja i način na koji se ocjenjuju rješenja i algoritam obavlja ostatak za nas. Ipak, kada postoji, potraga koja koristi specifična znanja o problemu općenito će dati bolje rezultate od genetskog algoritma.

Genetski algoritmi se koriste u različitim područjima za rješavanje problema koji prividno nemaju sličnosti: od slaganja aminokiselina tako da dobivena struktura bude najstabilnija moguća, teorije igara za pronalazak najpovoljnijih strategija pa do predviđanja prihoda na burzi temeljem prošlih podataka. Cilj je ovog rada objasniti osnove genetskog algoritma te pokazati načine njihove primjene na nekima od spomenutih problema. Detaljnije se razmatra problem prekrivanja površine na kojem se iznose mogućnosti implementacije, uspoređuju rezultati i navode parametri genetskog algoritma.

2. Opis genetskog algoritma

2.1 Prikaz rješenja

Darwin je prije više od stoljeća ustvrdio da se vrste prilagođavaju okolišu kroz evoluciju. Stoljeće nakon Darwina, otkrivena je struktura kromosoma u kojima su zapisana sva svojstva jedinke. Ako se genetski materijal usporedi s abecedom, tada su slova u genetskom materijalu dušične baze adenin(A), timin(T), citozin(C) i gvanin(G). Sva živa bića imaju na jednak način zapisan genetski kod ovim nizovima dušičnih baza. Od ovih su dušičnih baza građene aminokiseline, njih oko 20 koje preuzimaju ulogu riječi u zapisu genskog materijala. Aminokiseline se redaju u lance i njihov slijed određuje sva urođena svojstva jedinke. Ako su dušične baze slova evolucije, tada se aminokiseline mogu predstaviti kao riječi, a njihov niz kao potpuna knjiga o jedinki. U genetskom algoritmu rješenje postaje jedinka, a zapis rješenja mora se također prikazati u obliku sličnom prirodnom.

Neka je rješenje problema niz cijelih brojeva. Niz brojeva može se u računalu predstaviti cijelim brojevima, može se promatrati binarne zapise tih brojeva ili primjerice poredati brojeve i zapisivati samo udaljenosti među susjednim brojevima. Koje predstavljanje je bolje određeno je problemom koji se rješava.

Pri dizajniranju prikaza rješenja treba analizirati slijedeće:

Da li su sva moguća rješenja predstavljena kodiranjem? Ukoliko neka rješenja nisu predstavljena, ne mogu biti ni pronađena.
Kakav je utjecaj prikaza na genetske operatore? Različiti načini prikaza mogu utjecati na brzinu ili kvalitetu genetskih operatora. Križanje može donositi viši stupanj različitih rješenja, mutacije mogu stvarati više ili manje slične jedinke.
Postoje li moguća redundantna rješenja? Poželjno predstavljanje ne sadrži više istih predstavljanja jednog rješenja jer se na taj način troši više spremničkog prostora, a rad algoritma se može znatno usporiti. Razlikuju se jednoliko i nejednoliko redundantna predstavljanja. Jednolika predstavljanja sadrže u prosjeku isti broj dodatnih kodiranja rješenja i u praksi su se pokazala znatno boljima od nejednolikih [Rothlauf, 2006]. Važno svojstvo je i sličnost redundantnih rješenja. Sličnost rješenja može se formalno definirati i naravno ovisi o mjeri koju definiramo za skup prikaza. Prikazi koji su jednoliko redundantni i čija su rješenja slična pokazuju ista svojstva kao i neredundantni prikazi, primjerice mogu biti za faktor sporije. Ipak, redundantna rješenja ne moraju u svim slučajevima biti lošija. Moguće je da više predstavljanja donese korist pri mutaciji ili rekombinaciji. Priroda donekle koristi redundatno kodiranje jer strukturalno različiti geni mogu nositi jednaka svojstva za jedinku.
Kakvo je smještanje srodnih svojstava? Ako rješenje sadrži povezana svojstva treba razmotriti koliko su daleko ta svojstva u prikazu. Primjerice, neka rješenje sadrži svojstva a i b čija je povezanost važna za kvalitetu rješenja i neka je rješenje predstavljeno nizom, moguće binarnim. Pokazuje se da je za većinu problema poželjno da se svojstava a i b kodiraju na bliska mjesta unutar prikaza rješenja. Pri križanju se tako može osigurati visok stupanj povezanosti koji odražava stvarnu povezanost svojstava. Smještanje srodnih svojstava povezano je sa sličnosti redundantnih rješenja, ukoliko postoje. Ukoliko postoje redundantna rješenja i međusobno nisu slična tada pri mutaciji i križanju dobivamo visok stupanj novih rješenja.

2.1.1 Predstavljanje binarnim nizom

Binarni niz je najčešće upotrebljavano predstavljanje u upotrebi genetskog algoritma. Binarnim prikazom može se predstaviti cijeli broj, odsutnost ili prisutnost nekog faktora u rješenju ili diskretni položaj unutar nekog intervala. Binarno kodiranje s k bitova može kodirati 2^krazličitih rješenja. Za binarni prikaz b₀b₁…b_n i broj B vrijedi:

(2.1),(2.2)

Binarno kodiranje se može koristiti i pri traženju ekstrema funkcije jedne varijable na određenom intervalu. Interval se podijeli na jednakih 2^kdijelova i svaki binarni zapis predstavlja redom broj intervala.

Binarnim nizom mogu se predstavljati i polja binarnih brojeva. Polje se kodira na isti način kao u programskom jeziku C, redom se spremaju redci jedan za drugim. Ako polje ima M stupaca, element (i,j) se sprema na mjesto i*M+j u nizu. Pri ostvarivanju genetskih operatora treba imati na umu da susjedni bitovi ( primjerice bit gore ili dolje u polju ) ne moraju biti spremljeni na susjedna mjesta niza. Ako takvi bitovi imaju međuzavisnost koja je važna za rješenje potrebno je razmotriti genetske operatore koji će bitove razmatrati zajedno.

Za binarne nizove općenito se može reći da nisu redundantni i da kodiraju sve brojeve iz intervala [0, 2^k–1 ]. Ukoliko se kodira broj, treba primijetiti da vrijednost svakog bita nema jednaku važnost za rješenje. U primjeru traženju maksimuma funkcije jedne varijable, rješenja se može kodirati tako da interval potrage podijelimo na 2^k dijelova. Može se pretpostaviti da postoji određena korelacija između udaljenosti broja od maksimuma ( lokalnog ili globalnog ) i dobrote koju to rješenje nosi. Drugim riječima, promatrana funkcija trebala bi biti povezana ili s konačnim brojem prekida ako se očekuje da genetski algoritam bude efikasan. Unutar nekog područja trebalo bi vrijediti da rješenje bliže maksimumu ima veću nagradu. Promjena u najvažnijem bitu rješenja pomiče to rješenje za pola veličine intervala, dok promjena u najmanje važnom bitu daje minimalne pomake po intervalu. Važnost pojedinog bita u binarnom predstavljanju eksponencijalno pada. Zbog toga je razlika u nagradi koju rješenje dobiva kada se maksimumu približi prvim bitom očekivano veća od nagrade za zadnji bit. Može se pokazati da je očekivano ponašanje genetskog algoritma da će u ovom slučaju eksponencijalno sporije otkrivati manje važne bitove [Rothlauf, 2006].

Važno je svojstvo binarnih brojeva da imaju Hammingov skok. Hammingova udaljenost među binarnim nizovima je broj bitova na odgovarajućim mjestima koji se razlikuju. Npr. Hammingova udaljenost brojeva 13₁₀=1101₂ i 14₁₀=1110₂ je 2. Brojevi 31 i 32 se u vrijednosti razlikuju za 1, ali se njihovi binarni oblici 31₁₀=011111₂i 32₁₀=100000₂razlikuju u svim mjestima, pa je Hammingova udaljenost 6. Zbog toga u traženju rješenja križanjem i mutacijom ponekad teško otkrivamo susjedna rješenja. Ovaj nedostatak ispravlja Grayev kod.

2.1.2 Prikaz Grayevim kodom

Osnovna ideja Grayevog koda je da se brojevi koji se po vrijednosti razlikuju za jedan razlikuju na samo jednom mjestu i zapisu, tj. da je Hammingova udaljenost susjednih brojeva 1. Binarni broj kodira se u Grayev kako slijedi: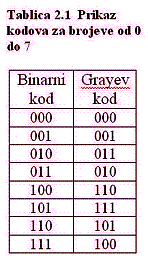

(2.3)

Pretvorba iz Grayevog u binarni kod je:

(2.4)

Praktična primjena pokazuje da u većini slučajeva nema bitne razlike između binarnog i Grayevog koda.

2.1.3 Broj s pomičnom točkom

Ponekad je najjednostavnije predstaviti rješenje kao broj s pomičnom točkom, primjerice ako je domena problema skup realnih brojeva. Realan broj zapisan je u računalu kao: predznak (1 bit), eksponent ( 8 bitova za jednostruku i 11 za dvostruku preciznost ) te frakcija ( 23 bita za jednostruku i 52 za dvostruku preciznost ).

Slika 2.1 Realan broj prema IEEE standardu

Ako se odabere ovaj način predstavljanja, treba napraviti posebne genetske operatore koji će djelovati na takvom zapisu.

Križanje daje realan broj koji je u intervalu čije granice određuju roditelji, ili u definiranoj blizini tog intervala. Mutacija može davati nasumičan broj unutar domene pretraživanja. Ipak, kako je za genetske algoritme domena obično jako velika, vjerojatnost da će takva mutacija dati korisno rješenje je vrlo mala. Zato se definira dinamički operator mutacije koji na počeku raspršuje rješenja po cijeloj domeni, a s napredovanjem eksponencijalno smanjuje raspršenje oko realnog broja kojeg se mutira. Više o dinamičkom operatoru mutacije reći će se i kasnije u poglavlju o primjeni genetskih algoritama. Kod mutacije posebnu pažnju treba posvetiti činjenici da su negativni eksponenti zastupljeni jednako kao i pozitivni, pa ako izaberemo eksponent nasumično, vjerojatnost je 50% da će on biti negativan i da će rješenje biti između –1 i 1. Zbog toga su poželjni drugačiji načini mutacije koji će biti uniformni.

Kao što je već rečeno za neke primjene binarne prikaze, važnost bitova u IEEE 754 prikazu realnog broja eksponencijalno pada k manje značajnim bitovima. To znači da se ispočetka maksimumu domene trebamo približavati najznačajnijim bitovima eksponenta i frakcije, a kasnije raditi fine pomake po manje značajnim bitovima. Ako je rješenje niz realnih brojeva, moguće je izdvojiti najznačajnije bitove frakcije u novi niz i postupno napredovanjem pretrage širiti taj niz, da bi on na kraju obuhvaćao sve bitove IEEE 754 prikaza na slici.

2.1.3 Graf i stablo

Grafovi se javljaju u velikom broju praktičnih problema kao što su povezivanje i simuliranje mreža, problem najkraćeg puta ili modeliranje međuzavisnosti jedinki.

Broj čvorova u grafu označava se s n. Broj bridova m, uz pretpostavku da nema višestrukih bridova među čvorovima je:

(2.5)

Najčešće predstavljanje grafa je poljem n*n gdje je (i,j) element polja 1 ako su čvorovi i i j povezani, a nula ako nisu. Može se uočiti da je dovoljno spremati i koristiti jednu polovicu polja ako graf nije usmjeren, jer je polje tada simetrično s obzirom na dijagonalu. Za ovaj oblik nije teško definirati genske operatore i svako moguće polje predstavlja jedan graf. Ako imamo više bridova među istim čvorovima ili usmjeren graf, još uvijek se može koristiti polje za prikaz grafa, tako da na mjestu (i,j) stoji broj bridova među i i j.

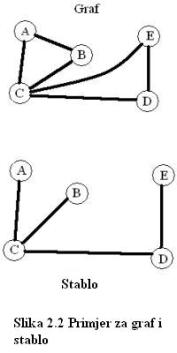Najvažniji poseban slučaj grafa je stablo. Stablo je povezan graf s n-1 bridova kod kojega između svaka dva čvora postoji samo jedan put.

Predstavljanje grafa je bitno lakše jer ne postoje dodatna ograničenja na povezanost i broj bridova, pa se ovdje razrađuje predstavljanje stabla. Zahtjevi koji se postavljaju pred predstavljanje stabla su:

Mora predstavljati sva moguća stabla s n čvorova. Za neke probleme ovo nije potrebno, no ovdje se razmatra općenit slučaj.
Ako postoje redundantna predstavljanja ona su jednoliko raspoređena po mogućim rješenjima.
Prikaz mora moći predstavljati samo stabla, ne i grafove. U suprotnom se velik dio rada može trošiti na provjeravanje svojstava stabla i eliminaciju grafova koji nisu stabla. Ukoliko genetski operatori generiraju grafove koji nisu stabla, dva su moguća pristupa: popraviti ih tako da iz grafa generiramo stablo ili ih kazniti odgovarajućom funkcijom ocjenjivanja.
Rekonstrukcija stabla iz odabranog predstavljanja mora biti brza. U funkciji ocjenjivanja najčešće se mora dekodirati stablo, a za velika drva neodgovarajuća složenost može znatno usporiti algoritam.

Postoji n^n-2 različitih stabala sa n čvorova. Za kodiranje stabla koriste se Prüferovi brojevi. Prüfer je 1912. dokazao da se svako stablo može bijektivno preslikati u niz ili broj od n-2 znamenki u bazi n.

Stupanj čvora definira se kao broj bridova kojim je čvor povezan s drugim čvorovima. U drvu stupanj čvora može biti od 1 do n-1. U primjeru sa slike 3, čvor C ima stupanj 4. Algoritam preslikavanja je jednostavan i koristi svojstvo da svako stablo ima barem dva čvora koji imaju stupanj 1. Označimo čvorove stabla proizvoljnim poretkom. Prüferov algoritam je:

Neka je i čvor stupnja 1 s najnižim brojem u stablu.
Jedini čvor s kojim je i povezan neka je j. Broj j dodaje se Prüferovom broju s desna.
Iz stabla se uklanja brid (i,j), a time se i čvor i.
Ponavlja se korake 1-3 dok ne ostanu dva čvora, tj. jedan brid.

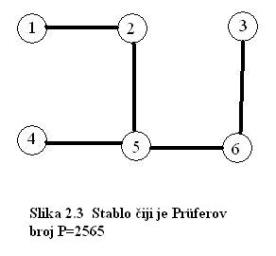
Provodi se algoritam na primjeru sa slike 1. Brojevima se označavaju čvorovi: A=1, B=2,…,E=5. Čvorovi stupnja 1 su {1,2,5}. Najniži broj među njima je 1, a njegov je susjed 3. Broj 3 dodaje se u Prüferov broj i uklanja brid (1,3). Sada su čvorovi stupnja jedan 2 i 5. Bira se broj 2 i u Prüferov niz dodajemo njegovog susjeda, broj 3. Prüferov niz je sada 33. Uklanjanjem brida (2,3) i čvor 3 postaje stupnja jedan. Bira se 3 i u Prüferov niz se dodaje njegova susjeda 4. Prüferov niz je 334. Preostala su dva čvora i jedan brid, algoritam je završio.

Nazovimo Prüferov broj P i uvedimo skup brojeva E. Inverzno preslikavanje iz Prüferovog niza u stablo je:

P se sastoji od n-2 znamenke. Sve znamenke od 1 do n koje se ne pojavljuju u P stavimo u skup E.
Neka je i najniži broj u E, a j prva lijeva znamenka Prüferovog niza. U drvo se dodaje brid (i,j).
Broj i se uklanja iz skupa E. Ako se j ne pojavljuje više nigdje u Prüferovom broju, broj j se dodaje u skup E. Broj j se uklanja sa početka Prüferovog broja.
Ponavljaju se koraci 2 i 3 dok u Prüferovom broju ima znamenaka. Kada nema, u skupu E su ostala dva broja, r i s. U stablo se dodaje brid (r,s).

Pojašnjava se rad algoritma na jednostavnom primjeru. Neka je Prüferov broj P=2565. U skupu E su brojevi {1,3,4}, jer se oni ne pojavljuju u broju P. Broj 1 je najniži među njima, a 2 je prva lijeva znamenka od P, pa se dodaje brid (1,2). Broj 1 se uklanja iz E i broj 2 iz P. Kako se 2 više ne pojavljuje u P, 2 se dodaje u E. Sada je E={2,3,4} i P=565. U stablo se dodaje brid (2,5). Broj 2 uklanjamo iz E i broj 5 iz P. Kako se 5 još jednom na samom kraju pojavljuje u P, ne dodaje se u E. Sada je E={3,4} i P=65. Dodaje se brid (3,6) i nakon njega (4,5). Sada smo uklonili sve znamenke od P, a u skupu E su znamenke 5 i 6. Dodaje se brid (5,6). Dobiven je graf sa slike 4.

Svojstva Prüferovog kodiranja zadovoljavaju sve spomenute zahtjeve iznesene za predstavljanje stabla kao rješenja genetskog algoritma. Treba još napomenuti da se algoritam realizira u složenosti O(n*log(n)) tako da se za operacije odabira najmanjeg elementa skupa E ili skupa čvorova stupnja 1 koristi prioritetni red (priority queue) ostvaren uz pomoć hrpe (heap) tako da umetanje i odabir imaju složenost O( log(n) ).

Nedostatak Prüferovog kodiranja je to što se slična stabla ne moraju kodirati na sličan način. Promjena u jednoj znamenci Prüferovog broja mogu sasvim izmijeniti izgled konačnog drva, pa se mutacijom i rekombinacijom dobiva visok stupanj lošijih rješenja. U praksi se pokazalo da su Prüferovi brojevi najpogodniji za stabla oblika zvijezde, gdje je jedan čvor povezan sa velikim brojem ostalih [Rothlauf, 2006].

Napomenimo kako je i stabla moguće kodirati kao polje bitova gdje bit označava prisutnost brida. Ovakvo predstavljanje omogućava i stvaranje grafova koji nisu stabla.

2.1.5 Automati

Automat je matematički model koji na temelju unaprijed određenih pravila i ulaza donosi odluke i daje povratnu informaciju, izlaz. Jednostavan primjer automata prikazuje se na slici 2.4. Ulaz ovog automata su dekadski brojevi, a izlaz je 1 ukoliko je zbroj do sada primljenih znamenaka djeljiv s 3 i 0 ukoliko nije. Početno stanje automata je 0. Automat treba tri stanja: ako se nalazi u prvom stanju zbroj do sada pristiglih znamenaka je 0, te 1 i 2 za ostala stanja prema nazivu. Stanje 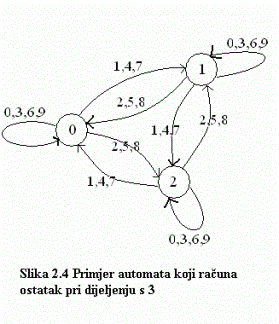automata nije varijabla programskog jezika, te se vrijednost samog stanja ne može mijenjati, već se informacija pohranjena u automatu određuje stanjem u kojem se automat trenutno nalazi. Primjerice, automat nema jednu varijablu u kojoj može pohraniti 0, 1 ili 2, već tri stanja, a pohranjena informacija ovisi u kojem od njih je automat trenutno.

Osnovna logika svakog automata je njegova funkcija prijelaza koja definira, s obzirom na trenutno stanje i ulaz, u koje novo stanje će prijeći automat i koji je mogući izlaz, pa funkcija prijelaza definira ponašanje automata. Pri predstavljanju automata u obliku pogodnom za genetski algoritam zapravo želimo kodirati funkciju prijelaza.

Pretpostavlja se, ne smanjujući općenitost, da automat ne daje poseban izlaz, već da se informacije dobivaju iz stanja u kojem se automat nalazi (Mooreov automat). Neka automat ima N stanja i S različitih ulaza. Funkcija stanja određuje novo stanje za svaku od N* S kombinacija trenutnog stanja i ulaza. Stanjima i ulazima pridjeljuju se brojevi od 1 do N, te od 1 do S. Pri predstavljanju funkcije prijelaza pravi se tablica N* S tako da na mjestu (i,j) zapišemo prijelaz u novo stanje iz stanja i e N uz ulaz j e S u binarnom obliku. Za svako stanje treba zapisati log₂N bitova, pa je veličina predstavljanja N* S ** log₂N. U tablici 2.2 dan je prikaz funkcije prijelaza za automat sa slike 2.4. Iz podebljanog elementa (2,3) zaključujemo: kada je automat u stanju 1 ( elementi tablice kreću od 1, a stanja od 0 i ulazi od 0) i ulaz je 2, automat prelazi u stanje 0=00₂. Napravljeno je kodiranje ulaznih znakova: kako su ulazni znakovi 0, 3, 6 i 9 međusobno jednaki za ponašanje automata svi su predstavljeni znakom 0. Isto vrijedi i za znakove 1={1,4,7} te 2={2,5,8}.

Operatori križanja i mutacije uvijek stvaraju tablicu koja predstavlja automat. Redundantna rješenja mogu se javiti kada postoje stanja koja nisu dohvatljiva, tj. u njih se ne može doći nijednim nizom ulaznih znakova. Automati se zajedno s genetskim algoritmima koriste u teoriji igara, o čemu će više riječi biti u dijelu o primjeni genetskih algoritama.

2.2 Funkcija ocjene

Funkcija ocjene svakom rješenju pridaje broj kojim ocjenjuje njegovu prilagođenost okolišu, tj. problemu koji se rješava. Još se naziva i funkcijom dobrote, funkcijom kazne ( ako je rezultat funkcije kazna koja se pridjeljuje svakom rješenju ) i funkcijom evaluacije.

Funkcija ocjene specifična je za svaki problem koji se rješava i ključna je za dobar rad algoritma budući da kontrolira nagrade koje će pojedina rješenja dobivati, pa tako i smjer evolucije.

S obzirom na povezanost približavanja najboljem rješenju i funkcije ocjene, probleme se može razvrstati u tri kategorije:

Pozitivno korelirani problemi za koje će funkcija ocjene dati višu nagradu onim rješenjima koja su bliža ili izgledom sličnija najboljem rješenju. Ovo svojstvo može vrijediti na cijeloj domeni ili na dijelovima domene za lokalne maksimume. Što je veća pozitivna korelacija problem je lakše rješiv. Ova vrsta problema pogodna je za genetske algoritme.
Nekorelirani problemi kod kojih nema povezanosti između bliskosti rješenja s optimumom i nagrade koju daje funkcija ocjene. Genetski algoritam ne može iskoristiti prikupljene informacije da bi procijenio položaj novog rješenja.
Negativno korelirani su problemi kod kojih će rješenje koje je bliže optimumu dati manju nagradu. Kako genetski algoritam napreduje u smjeru boljih rješenja ova vrsta problema najgori je slučaj za genetske algoritme. Primjer ovakvog problema je traženje najnižeg područja u golf terena, pri čemu je taj minimum rupica na vrhu brijega.

Prikaz triju slučajeva dan je na slici 2.5, gdje je globalni ili lokalni maksimum smješten u ishodište koordinatnog sustava. Slika je preuzeta iz [Rothlauf, 2006].

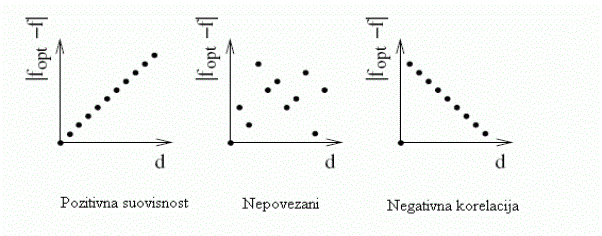
Slika 2.5 Korelacija blizine rješenja i nagrade koju rješenje dobiva u funkciji ocjene

2.3. Genetski operatori

2.3.1 Selekcija

Selekcija djeluje na čitavu populaciju i odabire jedinke koje će se eliminirati, odnosno one koje će se reproducirati i mutirati, te prenijeti u iduću generaciju. Pri selekciji i mutaciji treba biti pažljiv da se ne eliminira najbolje rješenje. Svojstvo genetskog algoritma da čuva najbolja rješenja naziva se elitizam.

Jednostavna selekcija bira iz trenutne generacije jedinke koje se prenose u iduću generaciju. Vjerojatnost prenošenja jedinke u iduću generaciju proporcionalna je njezinoj dobroti u odnosu na ukupnu dobrotu. Ako primjerice dobrota rješenja iznosi 5% od zbroja dobrota svih rješenja, tada je vjerojatnost prenošenja jedinke u novu generaciju pri svakom izboru 5%. Jedinka koja je jednom izabrana ima šansu ponovno biti izabrana, što znači da se u novoj generaciji mogu pojaviti duplikati. Jednostavnu selekciju možemo ostvariti tako da zbrojimo dobrote svih rješenja, neka je zbroj jednak D_u. Interval [0,1] podijelimo na D_udijelova i svakom rješenju pridijelimo podinterval proporcionalan njegovoj dobroti. Općenito se jednostavna selekcija provodi u vremenu O(n*log(n)), jer je se svaki izbor ostvaruje tako da se za broj izabran na sreću traži interval kojem broj pripada, što se ostvaruje u vremenu O(log(n)).

Selekcija sortiranjem obavlja se tako da se jedinke sortiraju po vrijednosti dobrote ( ili kazne ) i potom izabere određen broj najboljih jedinki. Ovakav postupak sortiranja dovodi do brze konvergencije prema lokalnim maksimumima. U svakom koraku gube se mogući vrijedni dijelovi manje loših rješenja.

Turnirska selekcija bira u svakom koraku k jedinki. Jedinke se uspoređuju međusobno i najbolja jedinka se izabere za daljnje djelovanje operatora križanja ili mutiranja, ili se jednostavno prenosi u sljedeću generaciju. Moguća je i turnirska eliminacija gdje se određen lošiji dio od k jedinki eliminira.

Eliminacijska selekcija eliminira dio lošijih rješenja i potom od preživjelih jedinki stvara nova rješenja koja nadomještaju eliminirana. Za eliminacijsku selekciju izračunava se kazna za svako rješenje i vjerojatnost eliminacije je proporcionalna kazni, slično kao kod jednostavne selekcije. Eliminirane jedinke ne mogu se ponovno eliminirati. Prednost eliminacijske selekcije nad jednostavnom selekcijom je što ne stvara istovjetna rješenja. Primjer eliminacijske selekcije dan je kasnije u problemu prekrivanja površine.

2.3.2 Križanje

Križanje je operator koje iz dviju jedinki stvara novu, poželjno sa svojstvima obaju ishodišnih jedinki. Dvije jedinke koje su sudjelovale u nastanku nove nazivamo roditeljima, a novu jedinku djetetom. Rješenje se u ovom dijelu teksta naziva jedinka ili kromosomom po uzoru na biološko križanje (crossover) kromosoma. Prije križanja moguće je provjeravati da li su roditelji jednaki. U tom slučaju i dijete će biti jednako roditeljima. Moguće rješenje za uklanjanje duplikata je u tom slučaju mutirati jednog od roditelja.

Križanje s jednom točkom prekida nasumično odabire točku unutar kromosoma i izmjenjuje dio nakon točke prekida sa drugim roditeljem. Nije svejedno da li se uvijek zamjenjuje dio nakon ili prije točke prekida. Primjerice, ako se uvijek zamjenjuje dio 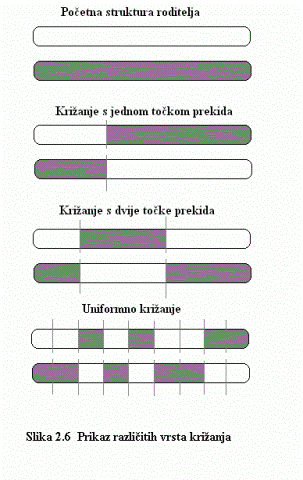nakon točke presjeka, dijete će uvijek imati početni dio od prvog roditelja. Rješenje je nasumično birati roditelje ( poredak nije važan ) ili nasumično odlučivati o tome koji dio se zamjenjuje. Križanje s dvije točke prekida također je često u praksi. Općenito križanje može biti s proizvoljno mnogo točaka prekida, dok je taj broj prekida manji od broja bitova.

Uniformno križanje za svaki dio (bit) kromosoma djeteta bira hoće li ga dijete naslijediti od prvog ili drugog roditelja. Najčešće je vjerojatnost nasljeđivanja od svakog roditelja jednaka, 50%, ali mogući su i pristupi u kojima vjerojatnost nasljeđivanja ovisi o funkciji ocjene za roditelje. Poluniformno križanje podvrsta je uniformnog križanja gdje se točno pola bitova koji se razlikuju u roditeljima zamjenjuju. Primijetimo da je poluniformno križanje slično uniformnom s vjerojatnošću 50%, ali nije identično.

2.3.3 Mutacija

Zadaća je operatora mutacije unošenje raznolikosti u populaciju. Kao i u biologiji, mutacije se u najvećem broju slučajeva neće pokazati kao poboljšanje, ali su ukupno ključne za napredovanje populacije i izbjegavanje lokalnih maksimuma. Naime, može se dogoditi da su sva rješenja populacije okupljena oko nekog lokalnog maksimuma i da se samo križanjem ne može napredovati u potrazi. Mutacija će neke jedinke preseliti van područja lokalnog maksimuma i pomoći genetskom algoritmu da pronađe globalni maksimum.

Jednostavna mutacija svaki dio (bit) kromosoma mijenja s određenom vjerojatnošću koja je parametar algoritma. Miješajuća mutacija zamjenjuje dijelove rješenja. Ukoliko se radi o binarnom prikazu, tada broj jedinica i nula ostaje isti. Ova mutacija ne dovodi do kvarenja rješenja u problemu trgovačkog putnika, gdje je važno da se element niza ne promijeni u neki koji u nizu već postoji, kako bi rješenje ostalo permutacija. Invertirajuća miješajuća mutacija dodatno invertira dijelove rješenja.

Parametar mutacije p_Mne mora biti konstantan tokom izvođenja, pa se tako u idućem poglavlju prikazuje algoritam koji koristi promjenjivu vrijednost parametra mutacije.

3. Primjena genetskih algoritama

3.1 Teorija igara

Najpoznatija i jedna od najranijih primjena genetskog algoritma u teoriji igara je ponavljana dilema zatvorenika. Politolozi, sociolozi i evolucijski biolozi proučavaju ovu igru jer na jednostavan način predstavlja problem suradnje. Genetske algoritme prvi je na igru primijenio Robert Axelrod.

Policija je privela dvojicu zatvorenika i ispituje ih odvojeno. Koji su mogući ishodi? Ako oba priznaju krivnju, oba će dobiti zatvorsku kaznu. Ukoliko jedan od njih prizna, a drugi to ne učini, onaj koji prizna dobiti će malu, a drugi veliku kaznu. Konačno, ukoliko oboje ne priznaju moguća je minimalna kazna. Ishodi se formaliziraju kroz tablicu 3. Element tablice daje nagradu za određeno ponašanje, pa će igrač koji će dobiti manju kaznu imati veću nagradu.

Strategiju za igru predstavlja se konačnim automatom koji odluku donosi na temelju prošlih igara. Automat pamti tri posljednje igre. Za svaku igru postoje 4 moguća ishoda, prikazana tablicom 3.1, pa je ukupan broj mogućih ishoda 64. Pojedina strategija definira što će zatvorenik napraviti za svaku prošle 64 situacije[1]. Kako su dvije mogućnosti za svaku situaciju ( priznati ili ne priznati ), prostor rješenja je 2⁶⁴. Taj prostor rješenja moguće je predstaviti nizom bitova.

Promatrajmo niz od 64 bita i jednu njegovu poziciju, primjerice poziciju 27. Binarni zapis broja 27₁₀ je 011011₂. Rastavimo taj niz na 3 dijela od 2 bita: 01-10-11. Neka svaki dio označava jednu od 3 prošle igre koje pamtimo. Ako 0 označava priznanje, a 1 da zatvorenik nije priznao, tada 01-10-11 možemo tumačiti ovako: prije 3 igre ja sam priznao (01-10-11), a protivnik nije (01-10-11). Prije dvije igre ja nisam priznao (01-10-11), a protivnik jest (01-10-11). Prošlu igru oboje nismo priznali.

Na poziciju 27 može se spremiti 0 ili 1, što će označiti da je uz navedene tri prošle igre strategija zatvorenika da prizna (0) ili ne prizna (1). Niz od 64 bita na ovaj način pokriva odgovor na sve moguće ishode 3 prošle igre, jer svaka pozicija u nizu predstavlja jednu od 64 mogućih kombinacija triju prošlih igara. Uz ovakav način kodiranja automata strategije jednostavno je napraviti genetske operatore. Kodiranje je neredundantno i ne postoji mogućnost stvaranja nizova koji ujedno nisu rješenje, tj. svaki niz je neka strategija igre.

Odabir dobrih strategija obavlja se turnirskom selekcijom: strategije međusobno igraju igru ograničen broj puta i dobrota strategije je ukupan broj sakupljenih nagrada.

Robert Axelrod koji je proveo istraživanje otkriva da je genetski algoritam kao najbolju strategiju pronašao tzv. srebreno pravilo: na početku surađuj, a tada svaki put odigraj ono što je protivnik odigrao u prošloj igri. Ova jednostavna strategija ranije je bila poznata kao optimalna, pobijedivši u prethodnim istraživanjima brojne složenije strategije [Holland, 2004].

3.2 Slaganje proteina

Genetski algoritmi s uspjehom su upotrebljeni za otkrivanje strukture proteina. Primjer uspješno konstruiranog proteina prikazan je na slici 3.1[2]. Uz dani niz aminokiselina problem se sastoji u pronalaženju strukture koja će imati najmanju potencijalnu energiju i time biti najstabilnija. Ukratko se iznosi rad [Schulze-Kremer, 2007] koji opisuje pristup rješavanju genetskim algoritmom.

Najjednostavnije kodiranje, predstavljanje položaja svakog dijela proteina s tri koordinate Kartezijevog sustava, nije se pokazalo uspješno jer omogućuje rješenja gdje su atomi preblizu ili predaleko. Odabrani prikaz je opisivanje položaja gradivnih blokova uz pomoć prostornog kuta i udaljenosti.

Funkcija cilja zahtijeva izračun potencijalne energije. Budući da bi točno izračunavanje potencijalne energije zahtijevalo prekompleksne matematičke izračune, koriste se iskustvene konstante da bi se dobila aproksimacija.

Operator mutacije zamjenjuje slučajno odabrani kut novim, tako da je novi kut vjerojatnije onaj koji se češće pojavljuje u sličnim gradivnim blokovima dosad analiziranih proteina. Mutacija se razmatra za svaki kut proteina zasebno i kontrolirana je parametrom koji je promjenjiv za vrijeme izvođenja programa. Manje promjene izdvojene su u operator varijacije, koji svaki kut može podesiti za manju vrijednost od 1^o, 5^o ili 10^o.

Križanje se provodi zasebno poslije mutacije i varijacije. Ovisno o promjenjivim parametrima odabire se križanje s dvije točke prekida ili uniformno križanje s vjerojatnošću 50% nasljeđivanja od svakog roditelja.

Kao što je već spomenuto, algoritam je promjenjivo parametriziran i parametri se mijenjaju tokom izvođenja tako da se u početku traže krupni pomaci prema boljem rješenju. Na počeku izvođenja dominantan je operator mutacije i veći pomaci varijacije (10^o), dok je pri kraju izvođenja dominantno križanje s dvije točke prekida i fino podešavanje kuta (1^o). Algoritam ima malu populaciju rješenja i velik broj izvođenja. Daljnja poboljšanja moguća su u funkciji ocjene koja će davati bolje ocjene stabilnosti proteina.

3.3 Problem trgovačkog putnika

Problem trgovačkog putnika je NP težak problem. NP kao klasa problema označava nepolinomnu složenost, tj. za njih nisu ne postoje efikasni algoritmi rješavanja. Problem trgovačkog putnika je za zadane gradove i udaljenosti među gradovima naći obilazak svih gradova tako da se svaki grad obiđe jednom i vrati u početni grad, a da prijeđeni put ( ili plaćena cijena putovanja ) bude najmanja moguća.

Rješenje je permutacija gradova koja se tumači tako da prvi element predstavlja prvi grad, drugi element idući grad itd. Predstavljanje permutacije moguće je u najjednostavnijem obliku kao niz brojeva, kao matrica susjedstva i kao permutacijska matrica. Matrica susjedstva kao rješenje problema sadrži veze među gradovima koji su uzastopni u rješenju. Primjerice, ako se iz grada 1 ide u grad 3, na mjestu (1,3) u matrici zapisujemo 1. Matrica permutacije kodira permutaciju tako da je u i-tom retku j-ti element 1 ako i samo ako je i-ti element permutacije j. Matrični prikazi svode se na binarne što pogoduje genetskim operatorima, ali njihov je nedostatak kvadratna ovisnost o broju gradova, što se može pokazati nepraktično u rješavanju problema s više tisuća gradova.

Funkcija ocjene rješenja se temelji na cijeni putovanja za svako rješenje, koja se jednostavno dobiva zbrajanjem cijena među svaka dva uzastopna grada koja rješenje posjećuje.

Prirodna selekcija pokazala se boljom od turnirske selekcije zbog brzine i jednostavnosti, dok turnirska selekcija daje rutu nešto bližu optimalnoj.

Više je povoljnih izbora za operator križanja. PMX (partially matched crossover) odabire dvije točke prekida na permutacijskom nizu oba rješenja i izmjenjuje sadržaj unutar točaka prekida. Posebno se pazi da u nastalim rješenjima nema ponavljajućih gradova, jer bi rješenje bilo nevaljalo. Dobrim se pokazalo GSX križanje (greedy subtour crossover) koje uzima svojstva oba roditelja i unosi određenu slučajnost, detaljnije opisano u ( Sengoku 1998).

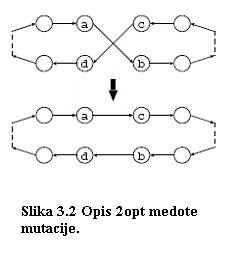
Za operator mutacije najbolja se pokazala 2opt metoda. Ova metoda radi tako da se izaberu dva para spojenih gradova, neka su nazvani AB i CD. Time se označava da su gradovi A i B, te C i D spojeni u ruti rješenja. Provjerava se da li se dobiva bolje rješenje ako se A spoji sa C i B sa D. Ukoliko je ta kombinacija bolja, ugrađuje se u rješenje. Metoda se prikazuje grafički na slici 3.2[3]. Problem ove metoda može biti zapinjanje u lokalnom minimumu.

Prikazani genetski algoritam uspješno savladava problem trgovačkog putnika za nekoliko stotina gradova.

3.4 Problem prekrivanja površine

U dvodimenzionalnom prostoru zadane su točke tako da svakoj točki pripada određena povezana površina. Potrebno je pronaći minimalan broj točaka tako da unija njihovih pripadajućih površina pokriva cijeli promatrani prostor. Zadatak je NP-težak, dakle ne može se riješiti u vremenu izvođenja koje bi bilo ograničeno polinomom. Iz definicije zadatka može se naslutiti eksponencijalnu složenost: mogu se pokušati sve kombinacije partitivnog skupa točaka, njih 2^N. Problem je ekvivalentan u sljedećim interpretacijama:

· Neka se promatra područje karte grada. Neka je moguće otvoriti uslužne objekte na samo određenim mjestima grada, tako da će svaki objekt usluživati kupce iz određenog geografskog prostora oko sebe. Koji je najmanji broj objekata koji se moraju otvoriti tako da svaki dio grada ima pripadajući bliski uslužni objekt?

· U auto-kampu se svjetiljke mogu postaviti samo na određene dijelove kako ne bi ometale promet i umanjivale prostor kampa. Koji je najbolji razmještaj takav da cijeli kamp bude osvijetljen?

· U izbornoj kampanji treba izabrati koje gradove posjetiti. Uz pretpostavku da će zainteresirani glasački iz bližeg područja posjetiti skup, koji je najbolji odabir gradova za turneju, tako da se osigura da kandidata čuju svi zainteresirani birači?

Općenitiji problem imao bi manje uvjete na dimenziju problema: dok je jednodimenzionalan problem trivijalan, trodimenzionalan problem je bitno teži. Pri rješavanju se pretpostavlja da je potrebno postaviti svjetiljke tako da osvjetljavaju čitav prostor, iako je čitav postupak jednak i za rješavanje ostalih varijanti problema. Ovdje je prikazano rješenje problema uz ograničenu veličinu početnog prostora i neka pojednostavljenja:

1. Prostor se predočava kvadratnom mrežom veličine 24x24 područja.

2. Svaka svjetiljka neka osvjetljava 8 susjednih područja ( od gore-lijevo do dole-desno ) i svoje područje, ukupno 9.

3. Svjetiljka može biti na bilo kojem mjestu promatranog područja.

Navedena pojednostavljenja ne mijenjaju algoritamsku složenost problema, već samo olakšavaju rad. Genetski algoritam napisan je objektno u jeziku C++ i u daljnjem tekstu se uz objašnjenje rada navode neki savjeti za implementaciju.

Za neke rasporede svjetiljki nije moguće prekriti cijelu promatranu površinu. Na samom početku program upali sve svjetiljke i provjerava da li su sva područja pokrivena. Ukoliko nisu, program prestaje s radom.

Ukoliko postoje svjetiljke koje jedine pokrivaju neko područje, one moraju biti upaljene u svakom valjanom rješenju. Takve svjetiljke se izdvajaju i u daljnjem toku rješavanja algoritam u svakom rješenju pali navedene svjetiljke, ukoliko nisu sve upaljene.

Prikaz rješenja

Rješenja se prirodno predstavljaju binarnim nizom duljine N, gdje je N broj svjetiljki. Naime, svaka svjetiljka može biti upaljena ili ugašena, a to je najjednostavnije prikazati binarnom znamenkom 0 ili 1. Osim niza bitova, za svako se rješenje pamti broj upaljenih svjetiljki, broj nepokrivenih područja te izračunata kazna, o čemu će više biti riječi u dijelu o funkciji ocjene i selekcije.

Rješenje je predstavljeno kao objekt koji osim varijabli sadrži i članske funkcije:

· Funkcija koja dekodira niz i broji nepokrivena područja te broj upaljenih svjetiljki

· Funkcija mutacije

· Operator AND nad nizom. Ovaj operator se koristi da bi se upalile svjetiljke koje moraju biti upaljene, kao što je prethodno objašnjeno. Dovoljno je takve svjetiljke spremiti u binarni niz te izvršiti AND nad tim nizom i svakim rješenjem.

· Operator jednakosti kojim provjeravamo jednakost dvaju rješenja.

· Operator usporedbe < kojim se leksikografski uspoređuju binarni nizove. Ovaj operator je potreban pri smještanju objekta u skup, kada se želi izbrojiti broj različitih rješenja ili izdvojiti jedinstvena.

Funkcija ocjene

Funkcija ocjene koristi već spomenutu člansku funkciju koja broji nepokrivena područja i broj upaljenih svjetiljki i temelji se na dodjeli kazne svakom rješenju. Kazna k = A*broj upaljenih svjetiljki + B*broj nepokrivenih područja. Kazna pojedinom rješenju sprema se u objekt koji predstavlja rješenje. Kako bi se izračunao broj nepokrivenih područja potrebno je dekodirati niz i obići čitavo područje pretraživanja za svako rješenje, pa je ovo najsporiji dio algoritma čija je složenost O(X*Y) gdje su X i Y veličine prostora koji treba osvijetliti.

Selekcija

Koristi se eliminacijska selekcija. Kako vrijednost kazne može biti velika u odnosu na razlike između najboljih i lošijih rješenja, prije same eliminacije obavlja se translacija kazni: od svih se kazni oduzima vrijednost najmanje kazne + konstanta K. Konstanta K određuje kaznu koje će imati i najbolje rješenje. Time i najbolja rješenja imaju mogućnost biti eliminirana. Ipak, najbolje do sada pronađeno rješenje pamti se kako bi se izbjegla mogućnost njegovog gubitka.

Vjerojatnost da će određeno rješenje biti eliminirano jednaka je relativnom iznosu translatirane kazne u odnosu na zbroj svih kazni. Primjerice, ako je kazna nekog rješenja 7, a zbroj svih kazni 70, tada je vjerojatnost 10% da će upravo to rješenje biti eliminirano. Broj eliminiranih rješenja zadaje se varijablom SELECT.

Križanje

Iz jedinki koje nisu eliminirane na sreću se biraju dvije jedinke čijim će se križanjem dobiti nova jedinka. Napisane su dvije funkcije križanja: križanje s jednom točkom prekida i uniformno križanje s vjerojatnošću nasljeđivanja 50% od svakog roditelja. U praksi se bitno boljom pokazalo uniformno križanje.

Pomoćne funkcije

Napisane su i dvije pomoćne funkcije:

funkcija koja ispisuje populaciju kao binarne nizove s dodatnim varijablama koje se pamte. Ova funkcija bila je od velike pomoći pri nastanku programa za uočavanje grešaka i sličnosti unutar populacija
funkcija koja ispisuje broj jedinstvenih rješenja unutar populacije i po potrebi uklanja redundantna. Funkcija je korisna pri analizi algoritma i populacije.

Parametri algoritma

Kao što je već spomenuto, algoritam se pri radu koristi konstantama čiju je vrijednost teško u potpunosti predvidjeti prije eksperimentalnog provjeravanja. U svrhu ispitivanja parametara napisan je pomoćni program koji je više od tisuću puta pokrenuo izvorni program s različitim parametrima. Pri tome je računat prosjek dobivenih rezultata iz 10 pokretanja za slabije kombinacije parametara, dok je za fino razlikovanje program pokrenut i do 100 puta s najboljim kombinacijama parametara. U trećem stupcu navedene su dobivene vrijednosti koje su se pokazale najboljima.

Tablica 3.2 Parametri genetskog algoritma u problemu prekrivanja površine.

Naziv parametra	Objašnjenje	Vrijednost	Ispitane mogućnosti
A	Koristi se u funkciji ocjene gdje se kazni dodaje A * broj upaljenih svjetiljki	1	1,2,3
B	Drugi faktor u izračunavanju kazne, kazna je jednaka A * broj upaljenih svjetiljki + B * broj nepokrivenih područja	2	1,2,3,5
K	Koristi se pri translaciji kazni i određuje najmanju kaznu, kaznu koju će imati najbolje rješenje	1	1,2,3,5
SELECT	Odabire koji dio rješenja će se eliminirati pri prelasku u novu generaciju i relativan je s obzirom na veličinu populacije	0.5	0.2, 0.3, 0.5, 0.7
MUTATION	Određuje vjerojatnost mutacije pojedinog bita. Najbolja vrijednost za mutaciju nije ista za sve testne primjere	0.003 i 0.0005	0.0002 0.001, 0.003, 0.005, 0.007
MUTCOEF	Ideja iza ovog koeficijenta je da ukoliko se određen broj generacija ne pronađe bolje rješenje, poveća MUTATION za određen faktor i tako dovede do raspršenijeg pretraživanja. Praktično ispitivanje pokazalo je da je najbolji izbor 1, tj. kada MUTCOEF nema utjecaja na povećanje mutacije.	1	0.9, 1.0, 1.1, 1.2
POPULATION	Veličina populacije	102	22, 42, 62, 102, 152, 202
RUNS	Broj generacija	5000

Primjer

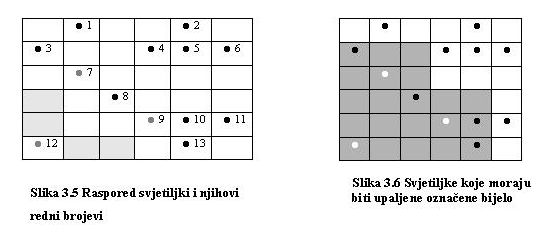
Na slici 3.5 prikazan je primjer polja veličine 6x6 s označenim pozicijama svjetiljki. Svjetiljke su označene brojevima. Ukupno je 13 svjetiljki, a kako svaka može biti upaljena i ugašena, broj mogućih kombinacija je 2¹³. Kako svaka svjetiljka pokriva prostor veličine 3x3 u čijem je središtu, može se primijetiti da su neka polja pokrivena sa samo jednom svjetiljkom, pa će ta svjetiljka u rješenju sigurno biti upaljena. To su svjetiljke 7,9 i 12, a pripadajuća polja koja jedino te svjetiljke pokrivaju su označena sivom bojom. Na slici 3.6 prikazane su spomenute svjetiljke upaljene i površine koje pokrivaju.

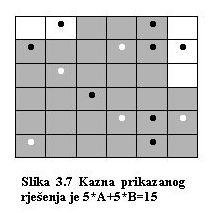
Na slici 3.7 prikazano je jedno moguće rješenje. Upaljene su svjetiljke s rednim brojevima 4,7,9,11 i 12. Kako se rješenja kodiraju binarno, ovo rješenje se prikazuje nizom u tablici 3.3.

Funkcija ocjene svakom rješenju daje kaznu u ovisnosti o broju upaljenih svjetiljki i broju nepokrivenih područja: kazna je jednaka A * broj upaljenih svjetiljki + B * broj nepokrivenih područja.

Ovdje je A=1 i B=2, pa je ukupna kazna 15.

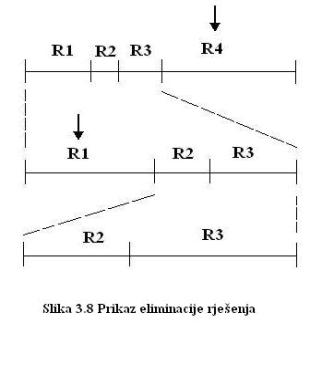
Na slici 3.8 prikazan je primjer eliminacijske selekcije. Prikazane kazne su 6,2,3 i 10 za rješenja R1, R2, R3 i R4, redom. U svakoj se generaciji eliminira određen broj rješenja tako da je vjerojatnost eliminacije jednaka udjelu kazne jedinke u ukupnom zbroju kazni. Eliminacija počinje stvaranjem intervala veličine jednake zbroju svih kazni, u ovom slučaju 21, i podjelom tog intervala na 4 podintervala veličine 6,2,3 i 10. Potom se nasumično (random) bira slučajan broj u cijelom intervalu i eliminira jedinka u čijem se podintervalu slučajan broj nalazi. U primjeru sa slike 3.8 prvo se eliminira jedinka R4. Od preostalih se podintervala stvara novi interval veličine 11 koji se podijeli na podintervale prema kaznama preostalih rješenja. Ponovno se bira slučajan broj koji ovaj put pada u podinterval pridružen R1, te se to rješenje eliminira i preostaju rješenja R2 i R3.

Na slikama 3.9 i 3.10 prikazano je križanje rješenja i rezultat. Pri križanju za svaki se bit bira s vjerojatnošću od 50% hoće li biti naslijeđen od prvog ili drugog rješenja.

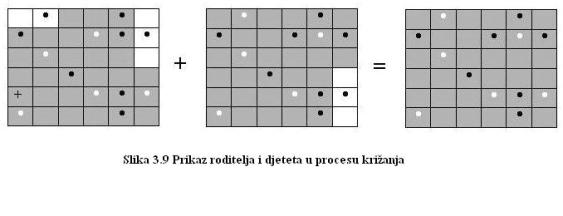
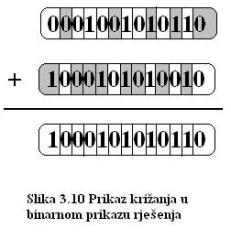
Kazna rješenja dobivenog procesom križanja je 6*A+0*B = 6. Ovo rješenje je ujedno i najbolje moguće za ovaj primjer. Može se primijetiti da postoji više jednako dobrih rješenja, pa je tako moguće u dobivenom rješenju ugasiti svjetiljku broj 11 i upaliti susjednu, broj 10, s istim učinkom.

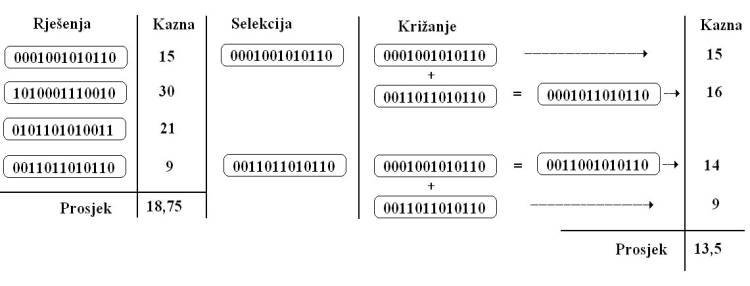
Slika 3.11. Prikaz dobivanja nove generacije iz početne

Genetski algoritam počet će svoj rad tako da nasumično odabere nizove od 13 bitova koji će postati početna generacija. Primjer jedne generacije genetskog algoritma dan je na slici 3.11. Odabrana je generacija od 4 rješenja. Svako rješenje se ocjenjuje i u svakoj se generaciji vrši selekcija kako je prikazano. Nakon selekcije, rješenja se križaju toliko puta koliko je jedinki eliminirano, kako bi veličina populacije rješenja bila stalna. U ovom jednostavnom prikazu nije pokazana mutacija rješenja. Dobivena je nova generacija rješenja čija je prosječna kazna manja od početne. Broj ponavljanja procesa je parametar programa.

Rezultati

Programski kod i testni primjeri korišteni za ispitivanje algoritma nalaze se u datoteci: Izvorni_kod_i_testni_primjeri.zip.

Prvi test primjer na kojem je algoritam detaljno ispitan sadrži 75 svjetiljki, pa je prostor pretraživanja 2⁷⁵. Optimalno rješenje za ovaj testni primjer je 33, a dobiveni rezultat je prosječno 33.325 na više od 50 pokretanja. 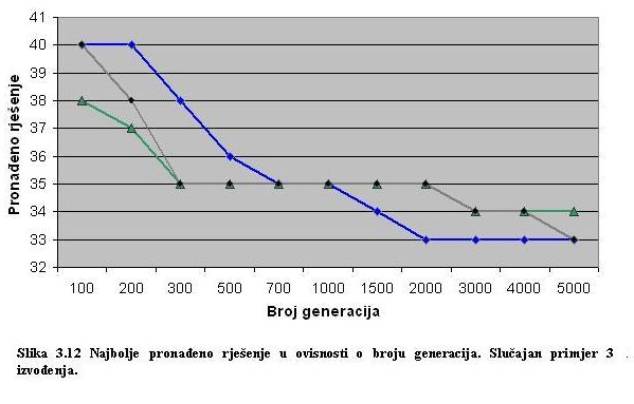Treba naglasiti kako je broj generacija ograničen na 5000, što na testnom računalu ( AMD Barton 2500+, 512 MB RAM, Linux Fedora 4 ), uz populaciju od 100 rješenja predstavlja vrijeme izvođenja od oko 5 sekundi. Na slici 3.12 prikazano je postupno pronalaženje rješenja u ovisnosti o napredovanju algoritma kroz generacije za tri test izvođenja. Skok sa 40 na 35 događa se unutar 700 generacija, a daljnje napredovanje je sve teže.

Drugi test primjer sadrži 246 svjetiljki. Optimalno rješenje za ovaj test problem je upaljenih 120 svjetiljki. Dobiveni rezultat je 122.8 na 10 izvođenja, uz parametre navedene u tablici 3.2. Povećanjem broja generacija ne dobiva se znatno na poboljšanju rješenja.

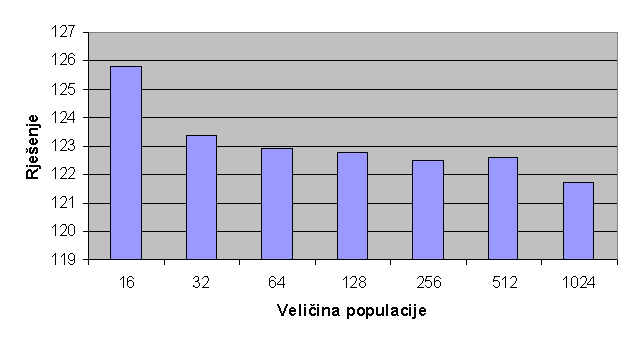
Slika 3.13 Odnos rješenja i veličine populacije

Najveći test primjer sadrži 416 svjetiljki. Najbolje rješenje koje je postigao genetski algoritam je 235 upaljenih svjetiljki. Na standardnim postavkama kao i u prva dva testna primjera, uz populaciju od 100 jedinki i 5000 generacija, algoritam u prosjeku pronalazi rješenje 239.

Usporedba GA s drugim rješenjima

Nakon predstavljenih rezultata može se postaviti pitanje: koliko je GA dobar u usporedbi s drugim rješenjima? Osim GA, napisana su još tri rješenja:

1. Rješenje koje slijeva na desno pamti moguće konfiguracije upaljenih svjetiljki. Rješenje je programski i algoritamski zahtijevno i njegov opis izlazi iz sadržaja ovog rada. Prostorna složenost iznosi , gdje je f zlatni rez (1.612…), a N broj područja koje treba osvijetliti. Vremenska složenost je . Obje složenosti su eksponencijalne i ovaj program radi za prva dva testna primjera, dok je treći testni primjer prevelik. Program pronalazi rješenje drugog testnog primjera za manje od 1 sekunde.

2. Pohlepno rješenje. Ovo rješenje redom slijeva na desno provjerava područja i za svako neosvijetljeno pronađe krajnje desnu svjetiljku koju upali. Rješenje je veoma brzo (N*log N).

3. Rješenje nasumičnim (random) gašenjem. Na početku se sve svjetiljke upale i potom se nasumično pokušavaju ugasiti svjetiljke. One koje se mogu ugasiti, ostaju ugašene.

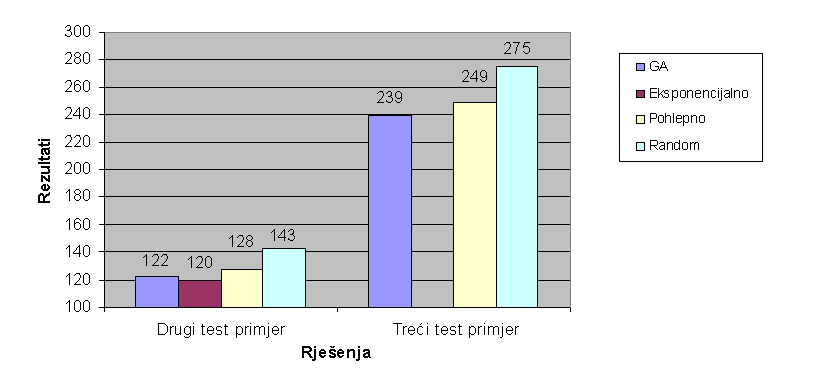
Slika 3.14 Usporedba GA s drugim algoritmima

Rezultati testiranja različitih rješenja prikazani su na slici 3.14. Zanimljivo je razmatrati najveći testni primjer. Nasumično rješenje daje daleko najlošije rezultate. Pohlepni algoritam dobra je alternativa s obzirom na jednostavnost i značajno ubrzanje. Genetski algoritam daje najbolje rezultate. Rezultate treba promatrati znajući da je bolja rješenja eksponencijalno teže pronaći što se više približava optimalnom rješenju, tako da je puno lakše ostvariti skok sa rezultata 275 na 249, nego skok s 249 na 239. Ovaj test primjer je prevelik za eksponencijalno rješenje.

Završna zapažanja

Za uspješnu primjenu genetskih algoritama ključni su izbor operatora i parametri algoritma. Često se najbolje kombinacije ne mogu predvidjeti prije same praktične provjere. Nekoliko opažanja je moguće izdvojiti:

Povećanje populacije ne dovodi nužno do boljih rješenja. Genetski algoritam pronalazi u prosjeku jednako dobra rješenja na drugom testnom primjeru za populacije veličine 100 i 200
Povećanje broja generacija donosi sve manja poboljšanja u rezultantnim rješenjima. Bolja rješenja je sve teže pronaći.
Najbolji koeficijent mutacije ne mora biti jednak za sve veličine rješenja. Za prvi test primjer najbolji je koeficijent mutacije 0.003, a za drugi test primjer koeficijent 0.0005. Umnožak koeficijenta mutacije i veličine rješenja u oba rješenja je približno jednak.
Križanje s jednom točkom prekida bitno je lošije od uniformnog križanja za ovaj problem. Prosjek rješenja penje se s 33.3 na preko 40 ako se ovim križanjem zamijeni uniformno.

4. Zaključak

Genetski algoritmi predstavljaju izrazito moćan i jednostavan alat za rješavanje teških rješenja potrage. Jednostavan možemo reći zbog toga što genetski algoritmi općenito ne zahtijevaju visok stupanj specijaliziranog znanja vezanog uz problem koji se rješava, iako takva znanja mogu unaprijediti algoritam.

Jedan od najtežih dijelova za dizajn genetskog algoritma je dobro predstavljanje rješenja. Najčešći je oblik predstavljanje binarnim nizom jer se takvim oblikom brzo radi sa strojnim instrukcijama i blizak je načinu na koji priroda “kodira” gene, pa se lako implementiraju genetski operatori. Ipak, za svaki problem može se izabrati i drugo predstavljanje koje je prirodno za problem, primjerice predstavljanje rješenja stablom ili konačnim automatom. Za svako od tih rješenja treba s obzirom na uvjete problema osmisliti genetske operatore.

Izbor genetskih operatora nije uvijek lagan zadatak. Ponekad nije moguće unaprijed predvidjeti utjecaj odabira pojedinog operatora na brzinu konvergencije rješenja, pa se mora implementirati više operatora i eksperimentalno utvrditi njihov utjecaj. Drugi parametri, kao što su veličina populacije i funkcija kazne, također se podešavaju na temelju ponašanja programa u praksi.

Problem je kandidat za rješavanje genetskim algoritmom ako:

· ima preveliki prostor rješenja da bi se cijeli mogao pretražiti

· ako uz optimalno rješenje postoje i druga rješenja za koja se na neki način može procijeniti koliko su dobra

· ako je nejasno kako bi se problem mogao riješiti koristeći znanja specifična za problem

U problemu prekrivanja površine genetskim algoritmom je riješen optimizacijski problem pronalaska najjeftinijeg prekrivanja površine od 2²⁴⁶mogućnosti. Ključni čimbenici algoritma su odabir operatora križanja i odabir koeficijenta mutacije. Pokazalo se da su rezultati bitno lošiji ako je koeficijent mutacije dva puta veći od optimalnog, a tek nešto lošiji za dva puta manji. Parametri koji utječu na brzinu rada su veličina populacije i broj generacija. Analizom veličine populacije, broja generacije i dobivenih rješenja odabrana je optimalna veličina populacije, a za bolje rezultate se predlaže povećanje broja generacija.

Genetski algoritmi se uspješno upotrebljavaju za rješavanje velikog broja različitih optimizacijskih rješenja. Njihova efikasnost ovisi o parametrima čije se optimalne vrijednosti određuju u praksi.

5. Literatura

[1] Golub, Marin. “Genetski algoritam: dio prvi”, verzija 2.3

Dostupno na adresi: http://www.zemris.fer.hr/~golub/ga/ga_skripta1.pdf

Datum posljednje izmjene: 27. rujna 2004., datum pristupa 25. travnja 2007.

[2] Mitchell, Melanie. “An introduction to genetic algorithms”, prvo izdanje

Massachusetts, MIT Press, 1999.

[3] Rothlauf, Franz. “Representations for genetic algorithms”, drugo izdanje

Berlin, Springer, 2006.

[4] Holland, John H., “Genetic algorithms”

Dostupno na adresi: http://www.econ.iastate.edu/tesfatsi/holland.GAIntro.htm

Datum nastanka: 14.ožujka 2005, datum pristupa 27. travnja 2007

[5] Marks, Robert E., “Playing games with genetic algorithms”

Dostupno na adresi: http://www.agsm.edu.au/~bobm/papers/shu.html

Datum nastanka: veljača 2000., datum pristupa: 14. travnja 2007

[6] Sengoku, Hiroaki, Yoshihara, Ikuo, “A Fast TSP Solver Using GA on JAVA”

Dostupno na adresi: www.gcd.org/sengoku/docs/arob98.pdf

Datum nastanka: 1998., datum pristupa: 28. travnja 2007

[7] Lovrečić, Vedran, “Genetski algoritam u primjeni”

Dostupno na adresi: http://www.zemris.fer.hr/~golub/ga/studenti/lovrecic/Genetski%20algoritam%20u%20primjeni.htm,

Seminarski rad, Fakultet Elektrotehnike i Računarstva, Zagreb, rujan 2005.

[8] Schulze-Kremer, Steffen, “Genetic Algorithms and Protein Folding”

Dostupno na adresi: http://www.techfak.uni-bielefeld.de/bcd/Curric/ProtEn/proten.html

Datum nastanka: 25. siječnja 2007, datum pristupa: 20. travnja 2007

[9] Wikipedia, “Crossover (genetic algorithm)”

Dostupno na adresi: http://en.wikipedia.org/wiki/Crossover_%28genetic_algorithm%29

Wikipedia, The Free Encyclopedia. Datum zadnje izmjene: 09. travnja 2007,

Datum pristupa: 28. travnja 2007.

[10] Fink, Thomas, «Protein folding»

Dostupno na adresi: http://www.tcm.phy.cam.ac.uk/~tmf20/PHYSICS/thesis/node12.html

Godina nastanka: 1998., datum pristupa 30.travnja 2007.

6. Sažetak

U prvom dijelu rada opisuju se genetski algoritmi. Naglasak je stavljen na predstavljanje rješenja, odnosno prilagođavanje problema genetskom algoritmu. Pokazani su načini predstavljanja binarnim nizom, realnim brojem, predstavljanje grafova i automata. Dan je pregled najčešće korištenih genetskih operatora.

U drugom dijelu opisuju se neke primjene genetskih algoritama. Pokazuje se kako su genetski algoritmi korišteni za određivanje optimalne strategije u teoriji igara, predviđanju strukture proteina i rješavanju problema trgovačkog putnika. Detaljnije se obrađuje problem prekrivanja površine na čijem se primjeru objašnjavaju parametri genetskog algoritma i njihovo praktično određivanje.

Zaključuje se kako su genetski algoritmi uz neke uvjete na problem moćan alat za rješavanje optimizacijskih problema pretraživanja.

[1] Za potpuno definiranu strategiju trebamo dodatne odluke za početak igre kada ne postoje već odigrane igre, ali to zbog jednostavnosti nećemo razmatrati.