Prva laboratorijska vježba iz Dubokog učenja

Gradijenti višeslojnih mreža, uvod u PyTorch, potpuno povezani duboki modeli, studija slučaja: MNIST

Predmet ove vježbe su unaprijedni duboki modeli za klasifikaciju. Pokazat ćemo da se ti modeli mogu promatrati ili kao višeslojne unaprijedne neuronske mreže ili kao produbljeni logistički modeli koje smo upoznali u nultoj vježbi. Oba pogleda vode na istu programsku izvedbu koja se temelji na optimiranju izglednosti parametara modela. Kako bismo olakšali razvoj i ubrzali eksperimentiranje, proučit ćemo mogućnost automatske diferencijacije koju danas nude brojni programski okviri za numeričku optimizaciju. Posebnu pažnju poklonit ćemo PyTorchu kao jednom od najčešće korištenih alata te kategorije.

Cilj vježbe je razviti sedam modula: data, fcann2, pt_linreg, pt_logreg, pt_deep, ksvm_wrap, i mnist_shootout. Modul data će biti nadograđena verzija istoimenog modula iz nulte vježbe. Modul fcann2 će sadržavati implementaciju dvoslojnog potpuno povezanog modela temeljenog na NumPyjevim primitivima. Organizacijski i izvedbeno, taj modul bi trebao biti vrlo sličan modulu logreg iz nulte vježbe. Moduli pt_linreg, pt_linreg i pt_deep implementirat će tri algoritma strojnog učenja u okviru PyTorch. Modul ksvm_wrap će umatati klasifikator s jezgrenim ugrađivanjem i potpornim vektorima izveden u modulu sklearn.svm biblioteke scikit-learn te omogućiti usporedbu s klasifikatorima temeljenima na dubokom učenju. Konačno, modul mnist_shootout će usporediti performansu do tada razvijenih klasifikatora na skupu podataka MNIST.

0a. Uvodne napomene o dubokim modelima

Duboki modeli strojnog učenja temelje se na apstraktnim reprezentacijama podataka do kojih dolazimo slijedom naučenih nelinearnih transformacija. U ovoj i sljedećoj vježbi razmatramo duboke modele koji su diskriminativni i unaprijedni. Diskriminativni model za dani podatak \(\mathbf{x}\) na izlazu izravno generira uvjetnu vjerojatnost zavisne varijable \(P(Y|\mathbf{X})\). Diskriminativne modele tipično koristimo kad na raspolaganju imamo označene podatke prikladne za nadzirano učenje. U unaprijednom modelu tok informacija je jednosmjeran što znači da (među)rezultati obrade ne mogu biti spojeni unatrag prema izlazu. Osnovni diskriminativni duboki model jest višeslojna unaprijedna neuronska mreža.

Umjetne neuronske mreže

Umjetne neuronske mreže su model strojnog učenja kojeg izražavamo usmjerenim grafom skalarnih procesnih jedinica koje nazivamo umjetnim neuronima. Jedan od važnih ciljeva razvoja neuronskih mreža je postavljanje računskog modela biološkog učenja odnosno razumijevanje mehanizama učenja u mozgu živog bića. Iako je vrlo srodno neuronskim mrežama, duboko učenje nema ambiciju modelirati biološke procese, nego proučava učenje kompozicijskih modela od praktičnog značaja koji mogu i ne moraju imati biološku interpretaciju.

Umjetni neuroni tipično provode afinu redukciju ulaznog vektora, što možemo sažeto prikazati izrazom \( f(\mathbf{w}^\top\mathbf{x}+b) \). Pri tome vektor \( \mathbf{x} \) predstavlja ulazne varijable, vektor \( \mathbf{w} \) i skalar \( b \) predstavljaju slobodne parametre koji se optimiraju postupkom učenja, dok \( f \) predstavlja tzv. prijenosnu funkciju umjetnog neurona. Uloga prijenosne funkcije je da u model unese nelinearnost. Ako za \( f \) odaberemo funkciju softmax, umjetni neuron će provoditi višerazrednu logističku regresiju. Ako za \( f \) odaberemo sigmoidalnu funkciju \( σ(s)=e^s/(1+e^s) \), umjetni neuron će provoditi binarnu logističku regresiju. Zbog boljeg učenja dubokih modela, sigmoidu danas istiskuje zglobnica (engl. rectified linear unit, ReLU) \( f(s) = \mathrm{ReLU}(s) = \max(0, s) \) .

Višeslojne unaprijedne mreže

Neuronska mreža s jednim ulaznim slojem, sofmaksom na izlazu, i gubitkom koji maksimizira izglednost parametara ekvivalentna je logističkoj regresiji. Međutim, na ovom kolegiju proučavamo "produbljene" modele koje dobivamo kad između ulaza i izlaza logističke regresije dodamo jednu ili više nelinearnih transformacija. Među njima, posebnu klasu čine unaprijedni modeli u kojima ne postoje povratne veze među neuronima. Takve modele možemo predstaviti acikličkim usmjerenim grafom gdje čvorovi odgovaraju neuronima, dok lukovi modeliraju povezanost neurona. Poput logističke regresije, unaprijedne duboke modele najčešće učimo gradijentnim spustom koji optimira izglednost predviđanja modela. Suprotno od logističke regresije, funkcija gubitka dubokih modela nije konveksna, što znači da ne postoji garancija da ćemo naći globalni optimum.

U ovoj vježbi posebno će nam biti zanimljive višeslojne mreže s potpuno povezanim slojevima. U takvim mrežama neurone možemo organizirati u slojeve \( S_k \) za koje vrijedi da neuroni sloja \( k \) na svojim ulazima primaju sve neurone sloja \( k-1 \). Za razliku od logističke regresije, višeslojni modeli mogu modelirati nelinearnu decizijsku granicu, ali po cijeni nekonveksne funkcije cilja.

U posljednje vrijeme popularno je, umjesto pojedinih neurona, čitav sloj promatrati kao kompoziciju linearnog i nelinearnog koraka obrade. Ako se dogovorimo da prijenosna funkcija vektorskog operanda odgovara konkatenaciji prijenosnih funkcija komponenata, dolazimo do sljedećeg sažetog zapisa k-tog sloja unaprijedne potpuno povezane mreže sa zglobnom aktivacijom:

\( \mathbf{s_k} = \mathbf{W_k}\cdot\mathbf{h_{k-1}} + \mathbf{b_k} \\ \mathbf{h_k} = \mathrm{ReLU}(\mathbf{s_k}) \)

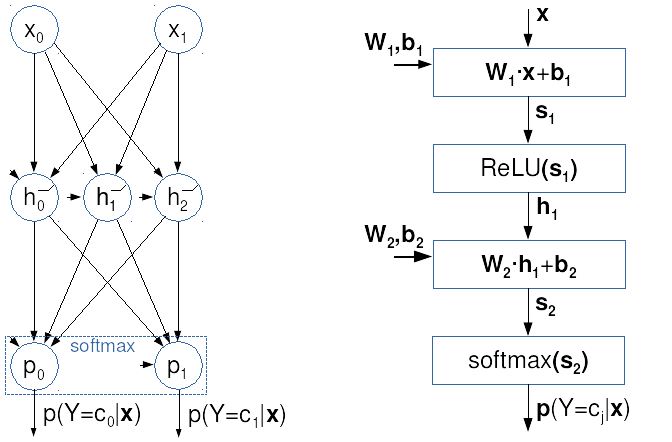
Sljedeća ilustracija prikazuje dva pogleda na istu potpuno povezanu unaprijednu mrežu. Na lijevoj strani je klasični prikaz gdje krugovi odgovaraju neuronima sa skalarnim izlazom i zglobnom prijenosnom funkcijom. Na desnoj strani je vektorizirani računski graf kojeg ćemo koristiti u ovom kolegiju: data

Gradijenti u dvoslojnom potpuno povezanom modelu

Razmotrimo sada kako bismo odredili gradijente u prethodno prikazanom primjeru dvoslojnog potpuno povezanog modela. Izrazimo klasifikacijski model vektorskim jednadžbama:

\( \mathbf{s_1} = \mathbf{W_1} \cdot \mathbf{x} + \mathbf{b_1} \\ \mathbf{h_1} = \mathrm{ReLU}(\mathbf{s_1}) \\ \mathbf{s_2} = \mathbf{W_2} \cdot \mathbf{h_1} + \mathbf{b_2} \\ P(Y|\mathbf{x}) = \mathrm{softmax}(\mathbf{s_2}) . \)

Naša funkcija gubitka biti će prosjek negativne log-izglednosti modela preko svih podataka:

\( L(\mathbf{W_1},\mathbf{b_1}, \mathbf{W_2},\mathbf{b_2}| \mathbf{X}, \mathbf{y}) = -\frac{1}{N} \sum_i \log P(Y=y_i|\mathbf{x}_i) \)

Vidimo da funkcija gubitka u podatku \( \mathbf{x}_i \) odgovara kompoziciji većeg broja jednostavnijih funkcija. Gubitak \(L\) ovisi o vjerojatnostima \(P\) koje ovise o linearnoj klasifikacijskoj mjeri drugog sloja \(\mathbf{s_2}\) koja ovisi o skrivenom sloju \(\mathbf{h_1}\) i parametrima \(\mathbf{W_2}\) i \(\mathbf{b_2}\). Skriveni sloj \(\mathbf{h_1}\) ovisi o svojoj linearnoj mjeri \(\mathbf{s_1}\), koja konačno ovisi o parametrima \(\mathbf{W_1}\) i \(\mathbf{b_1}\) te podatcima \(\mathbf{x}\). Stoga gradijente gubitka obzirom na parametre određujemo ulančavanjem. Parcijalne derivacije gubitka po j-tim retcima \( \mathbf{W_2} \) i \( \mathbf{b_2} \) biti će vrlo slične onom što smo imali u višerazrednoj logističkoj regresiji. U obzir ćemo uzeti algebarsku strukturu problema, tj. da vrijedi: \( \partial {s_2}_{ij}/ \partial \mathbf{W_2}_{k:} = \partial {s_2}_{ij}/ \partial \mathbf{b_2}_{k:} = 0, \; \forall k \neq j \; . \) Da bismo postigli kompaktniji zapis k-ti redak matrice \(\mathbf{W_2}\) označit ćemo kao \(\mathbf{W_2}_{k:}\). Nadalje, rezultat ćemo izraziti uz pomoć matrice aposteriornih vjerojatnosti \(\mathbf{P}\) te matrice vektorski kodiranih oznaka \(\mathbf{Y'}\) koje smo uveli u nultoj vježbi. Na kraju dobivamo sljedeće izraze:

\( \frac{∂L_i}{∂\mathbf{W_2}_{j:}} = \frac{∂L_i}{∂{s_2}_{ij}} \cdot \frac{∂{s_2}_{ij}}{∂\mathbf{W_2}_{j:}} = ({P}_{ij} - {Y'}_{ij}) \cdot \mathbf{h_1}_i^\top \; , \\ \frac{∂L_i}{∂b_{2j}} = \frac{∂L_i}{∂\mathbf{s_2}_{ij}} \cdot \frac{∂\mathbf{s_2}_{ij}}{∂b_{2j}} = ({P}_{ij} - {Y'}_{ij}) \; . \)

Put do gradijenata po \(\mathbf{W_1}\) i \(\mathbf{b_1}\) nešto je složeniji, jer gradijente treba propagirati preko svih komponenata drugog sloja. Međutim, to propagiranje nije komplicirano jer Jakobijan linearnog sloja odgovara matrici težina, dok je Jakobijan zglobnice dijagonalna matrica koja na dijagonali ima nule i jedinice ovisno o predznaku odgovarajuće komponente prvog sloja. Kad konačno dođemo do linearne mjere prvog sloja, možemo iskoristiti izvode koje smo bili dobili u drugom sloju. Ovisnost linearne klasifikacijske mjere drugog sloja o parametrima drugog sloja posve je jednaka ovisnosti linearne mjere prvog sloja o parametrima prvog sloja. Stoga su analitički izrazi parcijalnih derivacija \(\partial \mathbf{s}_1/\partial \mathbf{W_1}\) vrlo slični odgovarajućim izrazima u drugom sloju:

\( \frac{∂L_i}{∂\mathbf{s_1}_{i}} = \frac{∂L_i}{∂\mathbf{s_2}_i} \cdot \frac{∂\mathbf{s_2}_i}{∂\mathbf{h_1}_{i}} \cdot \frac{∂\mathbf{h_1}_{i}}{∂\mathbf{s_1}_{i}} \cdot = (\mathbf{P}_{i:} - \mathbf{Y'}_{i:}) \cdot \mathbf{W_2} \cdot \mathrm{diag}([\![s_{1i:}>0]\!]) \;, \\ \frac{∂L_i}{∂\mathbf{W_1}_{j:}} = \frac{∂L_i}{∂{s_1}_{ij}} \frac{∂\mathbf{s_1}_{ij}}{∂\mathbf{W_1}_{j:}} = \frac{∂L_i}{∂{s_1}_{ij}} \mathbf{x_i}^\top \;, \\ \frac{∂L_i}{∂b_{1j}} = \frac{∂L_i}{∂{s_1}_{ij}} \frac{∂\mathbf{s_1}_{ij}}{∂{b_1}_{j}} = \frac{∂L_i}{∂{s_1}_{ij}} \)

U nastavku ćemo termin gradijent koristiti i za parcijalnu derivaciju gubitka po parametrima kao i za pojedine dijelove tog vektora. Točno značenje moći će se pogoditi iz konteksta. Jednaka konvencija koristi se i u znanstvenoj literaturi. Tako će se izraz četiri gradijenta, odnositi na lijeve strane gore navedene četiri jednadžbe.

Ovdje valja primijetiti kako naša ambicija nije brzo izračunati pojedine gradijente za pojedine podatke. Naprotiv, naš cilj je brzo izračunati sve gradijente za sve podatke oslanjanjem na optimirane biblioteke matrične algebre. S obzirom na to da najveći doprinos brzini možemo ostvariti memorijskim optimizacijama, model trebamo izraziti matričnim operacijama koje djeluju nad svim podatcima. Stoga ćemo, kao i kod logističke regresije gradijente svakog sloja računati odjednom za sve retke parametara i za sve podatke.

Međutim, za razliku od logističke regresije, u dubokim mrežama moramo donijeti odluku o redoslijedu računanja gradijenata (npr. hoćemo li prije računati \(\frac{∂L_i}{∂\mathbf{b_1}}\) ili \(\frac{∂L_i}{∂\mathbf{b_2}}\)). Putokaz za rješavanje tog rebusa daje nam algoritam širenja unatrag.

Računanje gradijenata širenjem unatrag

U prikazanim jednadžbama možemo uočiti jednu specifičnost dubokih modela: vidimo da se parcijalna derivacija \( \frac{∂L_i}{∂\mathbf{s_2}_i} \) javlja u sva četiri gradijenta po parametrima funkcije gubitka. Tu specifičnost možemo iskoristiti kako bismo do željenih gradijenata došli uz minimalni računski napor. Parcijalne derivacije funkcije cilja po čvorovima računskog grafa nećemo morati računati više od jednom ako ih budemo računali unatrag, od izlaza prema ulazu mreže. Taj jednostavni ali vrlo efikasni pristup formalizira algoritam širenja unatrag (engl. backprop).

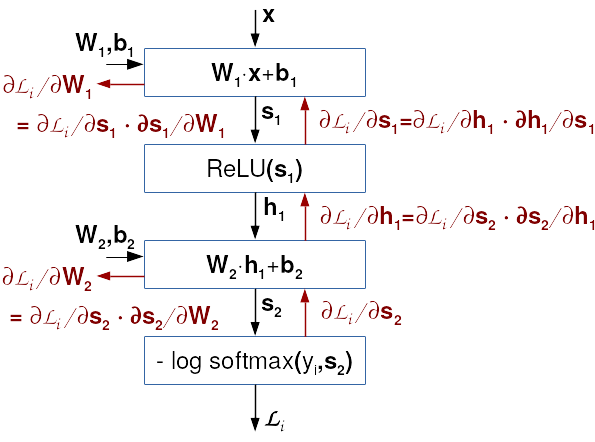
Postupak širenja pogreške unatrag prikazali smo na sljedećoj slici. Crne strelice prikazuju evaluiranje modela i računanje gubitka u zadanom podatku (tzv. unaprijedni prolaz, engl. forward pass). Crvene strelice prikazuju postupno računanje gradijenata prema algoritmu širenja unatrag (tzv. unatražni prolaz, engl. backward pass).

data

Sad se čini da su nam poznate sve komponente rješenja našeg problema. Znamo kako računati gradijente s obzirom na pojedine parametre, kao i kojim redoslijedom to obaviti. Međutim, htjeli bismo prije kraja još jednom naglasiti dva netrivijalna detalja. Prvi detalj je petlja po podatcima. Ako želimo uživati prednosti optimiranih biblioteka i izbjeći iteriranje u Pythonu, onda svaki pojedini gradijent trebamo odjednom izračunati za sve podatke. Ako imamo 100000 podataka, prvo ćemo izračunati 100000 redaka matrice \( \mathbf{G}_\mathbf{s_2} = [ (\frac{∂L_i}{∂\mathbf{s_2}_{i}})_{i=1}^N ] \), zatim 100000 redaka matrice \( \mathbf{G}_\mathbf{h_1} = [ (\frac{∂L_i}{∂\mathbf{h_1}_{i}})_{i=1}^N ] \), itd. Ovakav pristup je vrlo neobičan za inženjere koji su navikli sve pisati u vlastitom aranžmanu, jer strahovito povećava memorijske zahtjeve postupka. Međutim, tu cijenu moramo platiti, jer u suprotnom naš algoritam ne bismo mogli izraziti optimiranim lego-kockicama za matrične operacije pa bi nam učenje bilo sporije za nekoliko redova veličine.

Drugi detalj je računanje gradijenata težina. Ovdje vam preporučamo da umjesto odvojenog računanja gradijenata po retcima težina (kao što sugeriraju gore navedene jednadžbe) koristite pristup kojeg smo u nultoj vježbi pokazali na logističkoj regresiji (isp. odjeljak 0d uvodne vježbe). Naime, nije previše teško pokazati da se kompletna matrica gradijenata (koja se u iteraciji gradijentnog spusta naprosto dodaje matrici težina) može izraziti jednostavnim matričnim umnoškom. Gradijente težina u k-tom sloju \(\mathrm{grad}(\mathbf{W_k}) \) dobivamo množenjem transponirane matrice gradijenata gubitka po linearnoj mjeri k-tog sloja u svim podatcima \(\mathbf{G}_\mathbf{s_k}\) s matricom svih ulaza u k-ti sloj \(\mathbf{H}_{k-1}\). Na sličan način računamo i sve gradijente po komponentama pomaka k-tog sloja. Ovdje nam umjesto matričnog množenja treba zbrajanje stupaca matrice \(\mathbf{G}_\mathbf{s_k}\), a za to možemo koristiti funkciju np.sum.

U konkretnom primjeru naše dvoslojne mreže, imali bismo sljedeći redoslijed računanja parcijalnih derivacija funkcije gubitka:

  1. gradijenti gubitka obzirom na linearnu mjeru drugog sloja u svim podatcima:
  2. gradijenti gubitka obzirom na parametre drugog sloja
  3. gradijenti gubitka obzirom na nelinearni izlaz prvog sloja u svim podatcima:
  4. gradijent gubitka obzirom na linearnu mjeru prvog sloja u svim podatcima:
  5. gradijenti gubitka obzirom na parametre prvog sloja:
Izbjeljivanje podataka i inicijalizacija parametara

Kod modela učenih s gradijentnim spustom početna inicijalizacija parametara predstavlja jako važnu odluku. Kod latentnih slojeva aktiviranih zglobnicom, aktivacije moraju biti centrirane oko nule tako da zglobnica dođe do izražaja. Primjerice, kad bi svi ulazi bili pozitivni i kad bi sve težine bile pozitivne, sve zglobnice bi bile propusne i učinak sloja bio bi u potpunosti linearan. To ne može biti dobro jer je kombinacija linearnih transformacija ponovo linearna transformacija, a znamo da linearne transformacije imaju puno manji kapacitet od duboke kompozicije nelinearnih transformacija. Pouka ove rasprave jest da će učenje dubokog modela dobro napredovati ako:

0b. Uvodne napomene o PyTorchu

PyTorch je biblioteka otvorenog koda za oblikovanje metoda strojnog učenja s naglaskom na sljedeće ključne mogućnosti:

Iako postoje i drugi slični alati (TensorFlow, MXNet, ...), PyTorch je trenutno najpopularniji među istraživačima, pogodan je i za početnike zbog čiste organizacije i dobre dokumentacije.

PyTorch podržava različite operacijske sustave. Za strojno učenje općenito najviše podrške ima i najažurniji je Linux. Najsvježije informacije o PyTorchu možete naći na službenim stranicama.

Ilustrirajmo zadavanje programa u PyTorchu na jednostavnom primjeru: 

import torch
# definiranje operacije
def f(x, a, b):   
    return a * x + b

# definiranje varijabli i izgradnja dinamičnog 
# računskog grafa s unaprijednim prolazom
a = torch.tensor(5., requires_grad=True)
b = torch.tensor(8., requires_grad=True)
x = torch.tensor(2.)
y = f(x, a, b)
s = a ** 2

# unatražni prolaz koji računa gradijent 
# po svim tenzorima zadanim s requires_grad=True
y.backward()
s.backward()               # gradijent se akumulira
assert x.grad is None      # pytorch ne računa gradijente po x
assert a.grad == x + 2 * a # dy/da + ds/da
assert b.grad == 1         # dy/db + ds/db

# ispis rezultata
print(f"y={y}, g_a={a.grad}, g_b={b.grad}")

Prvi dio prikazanog primjera definira običnu funkciju u Pythonu. Povratna vrijednost te funkcije transparentno će se uklopiti u računski graf PyTorcha.

Drugi dio primjera stvara objekte a, b i x tipa torch.Tensor koji će odgovarati listovima računskog grafa. Tenzori a i b imaju atribut requires_grad=True, što znači da če za njih PyTorch pri automatskom unatražnom prolazu izračunati gradijent. Pozivanje operacija *, + i ** stvara nove objekta tipa torch.Tensor koji su također čvorovi računskog grafa. Dalje ćemo objekte tipa torch.Tensor nazivati tenzorima. PyTorch pri izračunavanju vrijednosti čvorova računskog grafa pamti sve međurezultate koji su potrebni za računanje gradijenta. Detalje određuje algoritam za automatsku diferencijaciju kojeg možemo skraćeno zvati autograd.

Treći dio primjera računa gradijente s obzirom na čvorove y i s pozivima metode backward. Autograd provodi unatražnu propagaciju sve do a i b te tako računa njihov gradijent. Višestruki pozivi metode backward akumuliraju gradijente u atributu grad svakog od tenzora deklariranih s requires_grad=True. Primijetite da slijed poziva y.backward(); s.backward() postiže isti učinak kao i (y + s).backward().

Atribut grad također je primjerak razreda torch.Tensor, ali je najčešće odvojen od računskog grafa u kojem je njegov matični tenzor. Računanje viših derivacija možemo postići pozivanjem metode backward s argumentom create_graph=True, čime se traži da u računski graf uđu i derivacije tenzora.

Ako želimo iznova izračunati gradijent (npr. za neki drugi x), onda moramo poništiti postojeći gradijent kako bismo izbjegli akumuliranje. To možemo postići brisanjem atributa grad postavljanjem npr. a.grad=None.

Ako nam za neki proračun ne treba izračun gradijenta, dobro je izraziti ga u tijelu upravitelja konteksta torch.no_grad() koji isključuje Autograd (tada se PyTorch ponaša kao NumPy). Ovdje je primjer procedure koja računa konfuzijsku matricu na temelju vektora indeksa točnih oznaka y_true i predikcija y_pred te vraća konfuzijsku matricu dimenzija class_count×class_count. 

import torch.nn.functional as F

def multiclass_confusion_matrix(y_true, y_pred, class_count):
  with torch.no_grad():
    y_pred = F.one_hot(y_pred, class_count)
    cm = torch.zeros([class_count] * 2, dtype=torch.int64, device=y_true.device)
    for c in range(class_count):
      cm[c, :] = y_pred[y_true == c, :].sum(0)
    return cm

Ovaj primjer pokazuje da PyTorch omogućuje kopiranje tenzora (i izračuna) između različitih platformi/uređaja primjenom opcionalnog argumenta device, koji primaju sve funkcije PyTorcha koje stvaraju nove tenzore. Primijetite da pri tome tip podatka možemo zadati primjenom opcionalnog argumenta dtype. Umjesto pokazanog poziva funkcije torch.zeros mogli bismo navesti i eksplicitnu konverziju torch.zeros([class_count] * 2).to(dtype=torch.int64, device=y_true.device), koja bi dala jednak rezultat, ali bi prouzročila nepotrebno stvaranje jednog privremenog tenzora. Tipične vrijednosti argumenta device su torch.device('cpu') (glavni procesor i memorija) ili torch.device('cuda:0') (prvi GPU pod platformom CUDA). Uređaj možemo zadati i znakovnim nizom: device='cpu' ili device='cuda:0'.

Više informacija možete naći u službenoj dokumentaciji PyTorcha.

0c. Primjena PyTorcha u strojnom učenju

Program koji koristi PyTorch tipično sadrži sljedeće komponente:

  1. model predstavljen objektom tipa izvedenog iz torch.nn.Module koji tipično sadrži druge module s parametrima,
  2. procedure za učitavanje i obradu ulaznih podataka,
  3. petlju učenja.

Procedure za učitavanje i obradu podataka tipično uključuju:

  1. skup podataka – obično objekt tipa izvedenog iz torch.utils.data.Dataset
  2. komponente za predobradu podataka na procesoru,
  3. komponente za uzorkovanje podataka tj. određivanje redoslijeda učitavanja (torch.utils.data.Sampler),
  4. komponentu za paralelno učitavanje i predobradu podataka (torch.utils.data.DataLoader).

Elementi algoritma učenja tipično uključuju:

  1. procedure za inicijalizaciju parametara,
  2. funkciju gubitka,
  3. optimizacijski algoritam – obično objekt tipa izvedenog iz torch.optim.Optimizer,
  4. petlju za učenje koja pribavlja podatke, računa gradijente gubitka te primjenjuje korak optimizacije koji ažurira parametre.

Sljedeći kod prikazuje primjer modela koji obavlja afinu transformaciju: 

import torch

class Affine(torch.nn.Module):
  def __init__(self, in_features, out_features):
    super().__init__()
    self.out_features = out_features
    self.linear = torch.nn.Linear(in_features, out_features, bias=False)
    self.bias = torch.nn.Parameter(torch.zeros(out_features))

  def forward(self, input):
    return self.linear(input) + self.bias

Prikazani primjer sadrži podmodel tipa torch.nn.Linear (koji već sam po sebi podržava pomak, ali to radi primjera ne koristimo) i parametar tipa torch.nn.Parameter. Tip torch.nn.Parameter je izveden iz torch.Tensor i uglavnom služi za razlikovanje parametara od drugih tenzora (atribut requires_grad podrazumijevano se postavlja na True). Razred torch.nn.Module definira metode koje vraćaju iteratore po modulima (modules), po podmodulima (children), parametrima (parameters) itd. Metode s prefiksom named_ vraćaju parove imena (putova) i objekata, kao što pokazuje sljedeći primjer: 

>>> affine = Affine(3, 4)
>>> print(list(affine.named_parameters()))
[('bias',
  Parameter containing:
  tensor([0.000, 0.000, 0.000], requires_grad=True)),
 ('linear.weight',
  Parameter containing:
  tensor([[-0.2684,  0.2126, -0.4430],
          [ 0.3446, -0.2018, -0.4346],
          [-0.4756, -0.3453,  0.1401],
          [ 0.3257,  0.0911, -0.1267]], requires_grad=True))]

Module obično oblikujemo tako da mogu raditi nad mini-grupama podataka. Primjerice, poziv affine(torch.randn(5, 3)) rezultira tenzorom dimenzija (5, 4), pri čemu torch.randn(5, 3) stvara matricu slučajnih normalno distribuiranih elemenata.

Više o modulima se može naći u službenoj dokumentaciji. Različite procedure za inicijalizaciju parametara su u paketu torch.nn.init.

Sljedeći primjer demonstrira osnove učitavanja podataka: 

import numpy as np
import torch
from torch.utils.data import DataLoader

dataset = [(torch.randn(4, 4), torch.randint(5, size=())) for _ in range(25)]
dataset = [(x.numpy(), y.numpy()) for x, y in dataset]
loader = DataLoader(dataset, batch_size=8, shuffle=False, 
                    num_workers=0, collate_fn=None, drop_last=False)
for x, y in loader:
  print(x.shape, y.shape)

Primjer prvo generira slučajan skup od 25 slučajnih parova matrica 4x4 i skalara. Podatci se iz demonstrativnih razloga bez kopiranja prebacuju u tip numpy.ndarray pozivanjem metode numpy. Skup podataka predaje se konstruktoru razreda DataLoader čiji primjerak ostvaruje iteriranje po mini-grupama. Slijede neki bitniji argumenti koje prima konstruktor. Argument batch_size je veličina mini-grupe. Argument shuffle je logička vrijednost koja određuje hoće li se prije svakog prolaza odabrati nasumični redoslijed. Argument num_workers je broj paralelnih procesa za učitavanje podataka. Argument collate_fn je funkcija koja iz pojedinih podataka slaže mini-grupe. U podrazumijevanom slučaju collate_fn=None poziva se funkcija torch.as_tensor, što NumPyjev niz bez kopiranja pretvara u torch.Tensor. Argument drop_last je Booleova vrijednost koja određuje hoće li se ispustiti zadnja mini-grupa ako je preostalo manje ods batch_size elemenata za zadnu mini-grupu. U prikazanom slučaju program će 3 puta ispisati torch.Size([8, 4, 4]) torch.Size([8]) i jednom torch.Size([1, 4, 4]) torch.Size([1]). Više o učitavanju podataka se može naći u službenoj dokumentaciji.

Sljedeća procedura opisuje primjer iteracije kod nadziranog učenja: 

def supervised_training_step(ctx, x, y):
  ctx.model.train()  # postavljanje modela u stanje za učenje
  output = ctx.model(x)  # unaprijedni prolaz
  loss = ctx.loss(output, y).mean()  # izračun gubitka

  ctx.optimizer.zero_grad()  # postavljanje gradijenta u 0
  loss.backward()  # unatražni prolaz
  ctx.optimizer.step()  # primjena koraka optimizacije

ctx je pristupni objekt koji obuhvaća model model, funkciju gubitka loss i optimizacijski algoritam optimizer. x i y su ulazna i izlazna mini-grupa. Prvo se model postavlja u stanje za učenje jer može sadržavati module kao što su dropout ili normalizacija po podacima koji se pri učenju različito ponašaju nego kod evaluacije. Zatim se u unaprijednom prolazu računaju izlaz modela i srednji gubitak na mini-grupi. Nakon toga slijedi korak optimizacije. Objekt optimizer je tipa izvedenog iz torch.optim.Optimizer te referencira parametre.

Ovako izgleda jednostavan primjer stvaranja optimizatora: 

from torch.optim import SGD
optimizer = SGD(model.parameters(), lr=1e-2, weight_decay=1e-4)

Osnovni argumenti su parametri i veličina optimizacijskog koraka lr. Radi efikasnosti, PyTorch nudi mogućnost provođenja L2 regularizacije izravno u optimizatoru. Zbog toga se u konstruktoru pojavljuje argument weight_decay. Glavne metode optimizatora su zero_grad i step. Metodu zero_grad treba pozvati prije svakog računanja gradijenta ako ga ne želimo akumulirati. Metoda step izvršava korak optimizacije. U slučaju gradijentnog spusta, ta metoda umanjuje sve parametre za odgovarajući gradijent pomnožen veličinom koraka. Više o optimizatorima se može naći u službenoj dokumentaciji.

1. Generiranje linearno nerazdvojivih podataka

Rješenje ove vježbe slobodno preuzmite ovdje: data.py.

U dosadašnjim eksperimentima logistička regresija je postizala iznimno dobre klasifikacijske rezultate. To nije nikakvo čudo jer se pokazuje da aposteriorna vjerojatnost razreda podataka generiranih Gaussovim razdiobama s dijeljenom kovarijancom odgovara upravo sigmoidi afino transformiranih podataka. Istina, u našim smo eksperimentima mrvicu odstupili od teoretskih pretpostavki (naši razredi su imali različite kovarijance), ali rezultati pokazuju da to odstupanje nije bilo presudno. Sada ćemo situaciju malo otežati na način da pozitivne i negativne podatke generiramo nešto složenijim generativnim modelom.

Upute:

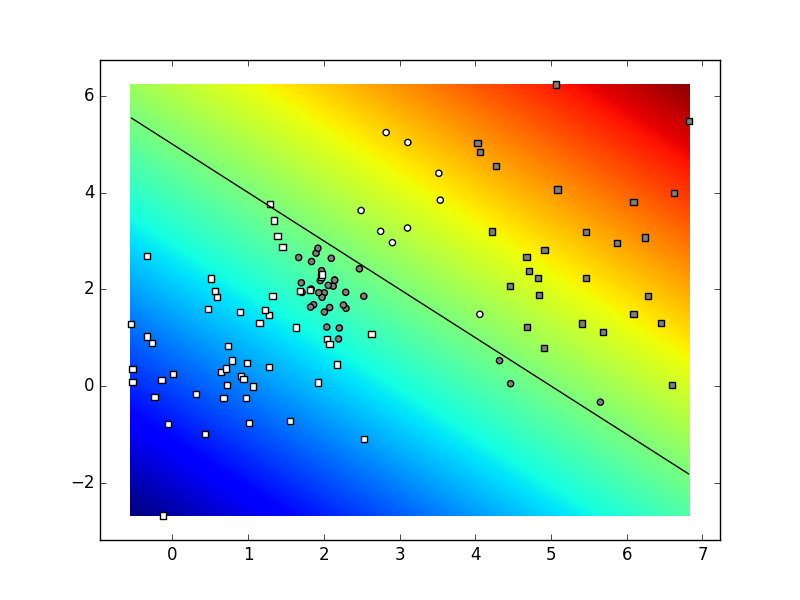
Izvedite potprogram sample_gmm_2d te ga ispitajte uz pomoć prethodno razvijenih potprograma za crtanje (graph_surface i graph_data). Ovisno o parametrima i stanju generatora slučajnih brojeva, vaš rezultat mogao bi izgledati kao na sljedećoj slici. Naši parametri bili su K=4, C=2, N=30.

data

Ako je rezultat izvođenja prihvatljiv, pohranite kod u datoteku data.py.

2. Višeslojna klasifikacija u NumPyju (20% bodova)

Oblikujte i izvedite modul fcann2 za rad s probabilističkim klasifikacijskim modelom s jednim skrivenim slojem prema uputama iz odjeljka 0a. Neka organizacija vašeg koda bude sukladna organizaciji modula logreg iz prethodne vježbe. Napišite metode fcann2_train, fcann2_classify. Isprobajte njihov rad na umjetnom skupu 2D podataka dvaju razreda dobivenih iz Gaussove mješavine od 6 komponenata.

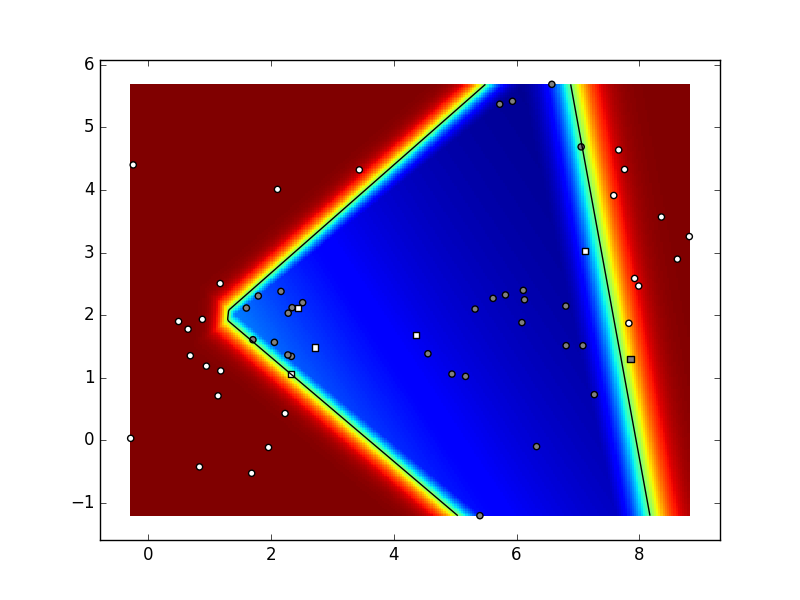
Ovisno o parametrima i stanju generatora slučajnih brojeva, vaš rezultat mogao bi izgledati kao na sljedećoj slici. Naši parametri bili su: K=6, C=2, N=10, param_niter=1e5, param_delta=0.05, param_lambda=1e-3 (koeficijent regularizacije), dimenzija skrivenog sloja: 5.

data

Ako je rezultat prihvatljiv, pohranite kod u datoteku fcann2.py.

3. Linearna regresija u PyTorchu (10% bodova)

Jednostavan primjer implementacije algoritma strojnog učenja u PyTorchu prikazat ćemo na potpunom primjeru optimizacijskog postupka za određivanje parametara pravca y = a * x + b koji prolazi kroz točke (1,3) i (2,5). 

import torch
import torch.nn as nn
import torch.optim as optim


## Definicija računskog grafa
# podaci i parametri, inicijalizacija parametara
a = torch.randn(1, requires_grad=True)
b = torch.randn(1, requires_grad=True)

X = torch.tensor([1, 2])
Y = torch.tensor([3, 5])

# optimizacijski postupak: gradijentni spust
optimizer = optim.SGD([a, b], lr=0.1)

for i in range(100):
    # afin regresijski model
    Y_ = a*X + b

    diff = (Y-Y_)

    # kvadratni gubitak
    loss = torch.sum(diff**2)

    # računanje gradijenata
    loss.backward()

    # korak optimizacije
    optimizer.step()

    # Postavljanje gradijenata na nulu
    optimizer.zero_grad()

    print(f'step: {i}, loss:{loss}, Y_:{Y_}, a:{a}, b {b}')

Zadatci:

Ako je rezultat prihvatljiv, pohranite kod u datoteku pt_linreg.py.

4. Logistička regresija u PyTorchu (20% bodova)

U ovom zadatku ćemo postupak logističke regresije izvesti uz pomoć PyTorcha. Dobiveni kod će biti oko dvostruko kraći od "ručnog rada" koji je bio predmet nulte vježbe. Glavne prednosti PyTorcha su u tome što ne moramo izvoditi gradijente te što se dobiveni program bez ikakvih izmjena može izvršavati na moćnim grafičkim karticama. Te prednosti će se pokazati presudnima kod velikih modela sa stotinama milijuna slobodnih parametara (kod malih modela procesori opće namjene mogu biti brži od grafičkih procesora zbog dugotrajnog prebacivanja podataka).

U PyTorchu model obično izražavamo nasljeđivanjem osnovnog razreda torch.nn.Module. Pritom je potrebno definirati konstruktor i funkciju forward koja predstavlja unaprijedni prolaz kroz model. Tenzore koji predstavljaju parametre modela kao atribute tipa torch.nn.Parameter. To nam omogučava jednostavan pristup parametrima modela korištenjem funkcije torch.nn.Module.parameters(). Modul za učenje logističke regresije bi mogao izgledati ovako: 

class PTLogreg(nn.Module):
  def __init__(self, D, C):
    """Arguments:
       - D: dimensions of each datapoint 
       - C: number of classes
    """

    # inicijalizirati parametre (koristite nn.Parameter):
    # imena mogu biti self.W, self.b
    # ...

  def forward(self, X):
    # unaprijedni prolaz modela: izračunati vjerojatnosti
    #   koristiti: torch.mm, torch.softmax
    # ...

  def get_loss(self, X, Yoh_):
    # formulacija gubitka
    #   koristiti: torch.log, torch.exp, torch.sum
    #   pripaziti na numerički preljev i podljev
    # ...


def train(model, X, Yoh_, param_niter, param_delta):
  """Arguments:
     - X: model inputs [NxD], type: torch.Tensor
     - Yoh_: ground truth [NxC], type: torch.Tensor
     - param_niter: number of training iterations
     - param_delta: learning rate
  """
  
  # inicijalizacija optimizatora
  # ...

  # petlja učenja
  # ispisujte gubitak tijekom učenja
  # ...


def eval(model, X):
  """Arguments:
     - model: type: PTLogreg
     - X: actual datapoints [NxD], type: np.array
     Returns: predicted class probabilites [NxC], type: np.array
  """
  # ulaz je potrebno pretvoriti u torch.Tensor
  # izlaze je potrebno pretvoriti u numpy.array
  # koristite torch.Tensor.detach() i torch.Tensor.numpy()

Primijetite da, za razliku od prethodne vježbe, točne oznake razreda podataka za učenje sada nazivamo Yoh_ umjesto Y_. Razlog tome je što unakrsnu entropiju lakše izražavamo kad su oznake smještene u matrici gdje retci odgovaraju podatcima, a stupci razredima (tzv. one-hot notacija). Ako podatak x_i odgovara razredu c_j, onda vrijedi Yoh_[i,j] = 1 te Yoh_[i,k] = 0 za k!=j ("one hot"). Podsjetimo se, tako organizirane oznake razreda u ranijim matematičkim izrazima nazivali smo matricom vektorski kodiranih oznaka \(\mathbf{Y'}\).

Struktura ispitnog programa bila bi vrlo slična ispitnim programima iz prethodne vježbe: 

if __name__ == "__main__":
  # inicijaliziraj generatore slučajnih brojeva
  np.random.seed(100)

  # instanciraj podatke X i labele Yoh_

  # definiraj model:
  ptlr = PTLogreg(X.shape[1], Yoh_.shape[1])

  # nauči parametre (X i Yoh_ moraju biti tipa torch.Tensor):
  train(ptlr, X, Yoh_, 1000, 0.5)

  # dohvati vjerojatnosti na skupu za učenje
  probs = eval(ptlr, X)

  # ispiši performansu (preciznost i odziv po razredima)

  # iscrtaj rezultate, decizijsku plohu

Zadatci:

Ako je rezultat izvođenja prihvatljiv, pohranite kod u datoteku pt_logreg.py.

5. Konfigurabilni duboki modeli u PyTorchu (20% bodova)

Naš sljedeći zadatak je proširiti izvedbu logističke regresije na način da omogućimo jednostavno zadavanje potpuno povezanih modela proizvoljne dubine. Nazovimo naš novi razred PTDeep. Neka sučelje tog razreda bude posve identično sučelju razreda PTLogreg, osim što ćemo u konstruktoru umjesto dimenzionalnosti podataka i broja razreda zadati listu cijelih brojeva koji će određivati broj neurona u svakom sloju. Dodatno, u konstruktoru ćemo zadati i aktivacijsku funkciju za skrivene slojeve dubokog modela. Nulti element te konfiguracijske liste određuje dimenzionalnost podataka, dok njen posljednji element (na rednom broju n-1) odgovara broju razreda. Elementi konfiguracije na indeksima od 1 do n-2 (ako postoje) sadržavaju brojeve neurona u skrivenim slojevima. Tako konfiguracija [2, 3] odgovara logističkoj regresiji dvodimenzionalnih podataka u tri razreda. Konfiguracija [2,5,3] odgovara modelu s jednim skrivenim slojem h koji se sastoji od 5 neurona: 

h = f (X * W_1 + b_1)
probs = softmax(h * W_2 + b_2)

U posljednjem primjeru dimenzije čvorova grafa trebaju biti kako slijedi (upitnici označavaju nepoznatu brojnost skupa podataka na kojem primijenjujemo model): 

  X     ... [?, 2]
  W_1   ... [2, 5]
  b_1   ... [1, 5]
  h_1   ... [?, 5]
  W_2   ... [5, 3]
  b_2   ... [1, 3]
  probs ... [?, 3]

Implementacija razreda PTDeep bit će vrlo slična implementaciji razreda PTLogreg. U konstruktoru moramo inicijalizirati matrice težina i vektora pomaka. S obzirom na to da broj slojeva može biti različit, matrice težina i vektore pomaka trebat će smjestiti u liste (nazovimo ih self.weights i self.biases). Slično kao u prethodnom zadatku, kako bismo iskoristili sve mogućnosti nadrazreda torch.nn.Module atribut koji predstavlja listu parametara treba biti tipa torch.nn.ParameterList, dok članovi te kolekcije trebaju biti tipa torch.nn.Parameter. Nelinearnost u skrivenim slojevima možete izraziti uz pomoć funkcija torch.relu, torch.sigmoid odnosno torch.tanh.

Napomena: PyTorch sadrži i razrede za potpuno povezani sloj torch.nn.Linear i unaprijedni model zadan nizom slojeva torch.nn.Sequential. Ipak, iz edukativnih razloga zadatak ćemo riješiti na već opisani način. Znatiželjni dodatno mogu zadatak riješiti korištenjem gotovih razreda.

Zadatci:

Ovisno o parametrima i stanju generatora slučajnih brojeva, vaš rezultat mogao bi izgledati kao na sljedećoj animaciji (naši parametri bili su: K=6, C=2, N=10, param_niter=1e4, param_delta=0.1, param_lambda=1e-4 (koeficijent regularizacije), config=[2, 10, 10, 2], ReLU).

data

Ako je rezultat izvođenja prihvatljiv, vaš kod pohranite u datoteku pt_deep.py.

6. Usporedba s jezgrenim SVM-om (10% bodova)

Podsjetite se na svojstva jezgrenog SVM-a (model, gubitak, optimizacija) te pročitajte dokumentaciju modula svm biblioteke scikit-learn. Oblikujte razred KSVMWrap kao tanki omotač oko modula sklearn.svm kojeg ćemo moći primijeniti na našim dvodimenzionalnim podatcima. S obzirom na to da će omotač biti jednostavan, učenje možemo provesti iz konstruktora dok predikciju razreda, dohvat klasifikacijskih mjera (potrebne za prosječnu preciznost) i dohvat potpornih vektora možemo izvesti u metodama. Neka sučelje razreda bude kako slijedi: 

'''
Metode:
  __init__(self, X, Y_, param_svm_c=1, param_svm_gamma='auto'):
    Konstruira omotač i uči RBF SVM klasifikator
    X, Y_:           podatci i točni indeksi razreda
    param_svm_c:     relativni značaj podatkovne cijene
    param_svm_gamma: širina RBF jezgre

  predict(self, X)
    Predviđa i vraća indekse razreda podataka X

  get_scores(self, X):
    Vraća klasifikacijske mjere
    (engl. classification scores) podataka X;
    ovo će vam trebati za računanje prosječne preciznosti.

  support
    Indeksi podataka koji su odabrani za potporne vektore
'''

Zadatci:

data

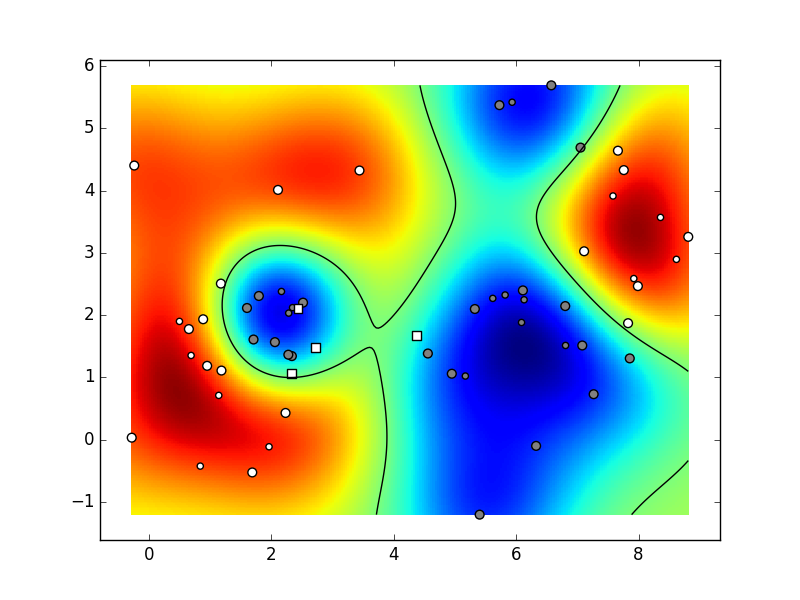
Ako je rezultat izvođenja prihvatljiv, pohranite kod u datoteku ksvm_wrap.py.

7. Studija slučaja: MNIST (20% bodova)

U dosadašnjim vježbama naučene modele nismo evaluirali na nezavisnom skupu za testiranje. Takvi eksperimenti ne bi nužno otkrili generalizacijski potencijal algoritama, jer se generativni modeli stvarnih podataka ne moraju moći opisati Gaussovim razdiobama. Zato ćemo se u ovoj vježbi posvetiti generalizacijskoj performansi na stvarnom skupu podataka MNIST.

MNIST predstavlja skup slika rukom pisanih znamenki od 0 do 9. Svaka znamenka predstavljena je slikom dimenzija 28x28 piksela. MNIST sadrži 60000 slika u skupu za učenje, i 10000 slika u skupu za testiranje. MNIST možemo jednostavno učitati sljedećim kodom: 

import torch
import torchvision

dataset_root = '/tmp/mnist'  # change this to your preference
mnist_train = torchvision.datasets.MNIST(dataset_root, train=True, download=True)
mnist_test = torchvision.datasets.MNIST(dataset_root, train=False, download=True)

x_train, y_train = mnist_train.data, mnist_train.targets
x_test, y_test = mnist_test.data, mnist_test.targets
x_train, x_test = x_train.float().div_(255.0), x_test.float().div_(255.0)
Ovaj pristup za preuzimanje podatkovnog skupa MNIST ponekad će završiti greškom 503. Ako se to dogodi, predlažemo sljedeću alternativnu proceduru:
  1. ručno downloadati MNIST s alternativnih stranica
  2. postaviti dataset_root na kazalo koje sadrži kazalo MNIST
  3. instancirati skup za učenje:
  4. jednako za skup za testiranje.

Sada su skupovi slika i indeksi razreda predstavljeni PyTorchevim tenzorima x_train, y_train, x_test i y_test. Do dimenzija podataka i broja razreda možemo doći jednostavnim propitivanjem oblika tih matrica. 

N = x_train.shape[0]
D = x_train.shape[1] * x_train.shape[2]
C = y_train.max().add_(1).item()

Pojedinačne slike možemo prikazati pozivom funkcije plt.imshow pri čemu preporučamo koristiti argument cmap = plt.get_cmap('gray').

Zadatci:

Ako je rezultat izvođenja prihvatljiv, pohranite kod u datoteku mnist_shootout.py.

8. Normalizacija po podatcima (bonus)

Proučite postupak normalizacije po grupi (engl. batch normalization) za potpuno povezane modele. Proširite duboki klasifikator iz zadatka 5 kodom koji normalizira izlaz linearnog dijela svakog skrivenog sloja tako da za tekuću grupu ima sredinu nula i jediničnu varijancu. Pripazite na to da parametre normalizacije valja mijenjati samo prilikom učenja. Usporedite dobivenu performansu s performansom osnovnih dubokih modela. Proučite probleme koji se mogu javiti pri učenju modela s normalizacijskim slojevima.

Za sve bodove potrebno je razviti vlastitu implementaciju, a ne koristiti torch.nn.BatchNorm1d.