Gotovo svaki računalni sustav upravlja s više aktivnosti koje se često odvijaju paralelno. Najjednostavnije ostvarenje upravljanja takvim sustavom jest da se za svaku nadgledanu aktivnost koristi po jedan proces ili dretva [1]. Aktivnosti u istom sustavu mogu dijeliti ista sredstva, ali pristup tim sredstvima treba nekako kontrolirati, tj. sinkronizirati, zbog mogućih problema pri istovremenom korištenju. „Istovremeni“ pristup može biti stvarno istovremeni u višeprocesorskim sustavima, dok je kod jednoprocesorskih sustava on samo prividno istovremen a nastaje zbog unaprijed nepredvidljivog raspoređivanja dretvi na jednom procesoru. Problem ispravne sinkronizacije općenito je vrlo složen i često je uzrok neočekivanim ispadima različitih programa. Jedan primjer koji može ilustrirati složenost problema je događaj koji se dogodio u upravljačkom sustavu robotske letjelice „Mars Pathfinder“ za vrijeme njene misije na Marsu [2]. Iako se takvi sustavi vrlo rigorozno ispituju napravljen je previd određenih mogućih stanja dretvi u sustavu, koja su se upravo i dogodila, te je sustav do dijagnosticiranja i ispravljanja tih grešaka bio neupotrebljiv.
Za ostvarenje kontrole pristupa sredstvima koriste se funkcije operacijskih sustava, takozvane funkcije sinkronizacije. Iako se sinkronizacija može obavljati s pomoću velikog broja mehanizama operacijskog sustava, najčešće korišteni mehanizmi sinkronizacije su semafori i monitori, detaljnije objašnjeni u nastavku.
Najčešće korišteni mehanizam sinkronizacije su semafori. Oni se mogu koristiti kao mehanizam međusobnog isključivanja – binarni semafori, ili kao brojila proizvoljnih sredstava ili događaja – opći semafori. Uz svaki se semafor veže vrijednost semafora. Za binarni su to vrijednosti „prolazan“ ili „neprolazan“, češće označavano s 1 i 0. Opći semafor može imati više vrijednosti. S obzirom na razne izvedbe općih semafora, u ovom radu koristit će se semafor koji može poprimiti samo nenegativne vrijednosti, što je najčešće korišten oblik semafora [7].
Jezgrine funkcije za rad sa semaforom su [1]:
• ČekajBSem(i), PostaviBSem(i) za binarni semafor te
• ČekajOSem(j), PostaviOSem(j) za opći, gdje indeksi i i j označavaju o kojem se semaforu radi.
Ukratko, funkcije s prefiksom „čekaj“ će pokušati smanjiti vrijednost semafora za 1 a da njegova vrijednost ne postane negativna, a funkcije „postavi“ povećavaju vrijednost semafora za 1. Izuzetak je funkcija PostaviBSem(i) koja ne smije dopustiti da se vrijednost semafora poveća iznad 1. U praktičnim ostvarenjima binarnog semafora može se umjesto vrijednosti 1 uzeti najveća vrijednost koju semafor može poprimiti (npr. MAXSHORT) te na taj način osigurati da semafor ima samo dvije vrijednosti, 0 koja je neprolazna i najveću moguću (MAXSHORT), koja označava prolaznu vrijednost.
Drugi, konceptualno drukčiji mehanizam sinkronizacije su monitori. Monitori su zapravo skup funkcija (monitorskih funkcija) s posebnim svojstvima, koje su ostvarene s pomoću funkcija jezgre operacijskog sustava.
Za svaki monitor uvijek vrijedi sljedeće: ukoliko je neka dretva aktivna u nekoj od funkcija koje pripadaju dotičnom monitoru (odnosno, za dretvu se kaže da je unutar monitora), svim ostalim dretvama nije dopušten ulazak u monitorsku funkciju. Poziv monitorske funkcije zaustavit će pozivajuću dretvu, ako se trenutno neka druga dretva već nalazi u monitoru. Kako u pojedinoj monitorskoj funkciji može biti uvijek aktivna samo jedna dretva, ona može pristupati nekim dijeljenim podacima, mijenjati te podatke, ispitivati uvjete koji su toj ili nekoj drugoj dretvi potrebni za nastavak rada. Kada dretva unutar monitorske funkcije ustanovi da joj uvjeti za nastavak rada nisu ispunjeni tada koristeći posebne jezgrine funkcije dretva se svrstava u red čekanja (red uvjeta). Pritom privremeno izlazi iz monitora i time omogućava da neka druga dretva uđe u monitor. U redu čekanja dretva će biti dok joj neka druga dretva, posebnom jezgrinom funkcijom, ne signalizira da može nastaviti s radom. S obzirom na nekoliko mogućih ostvarenja monitora, u ovom radu će se koristiti ostvarenje koje se i najčešće ostvaruje u operacijskim sustavima [8] iako će se funkcije nazvati slično onima korištenim u [1] (samo su imena slična s funkcijama u [1], ne i ponašanje!).
Jezgrine funkcije za ostvarenje monitora označavat će se sa:
• Uđi_u_monitor(m),
• Izađi_iz_monitora(m),
• Uvrsti_u_red_uvjeta(m, k),
• Oslobodi_iz_reda_uvjeta(m, k).
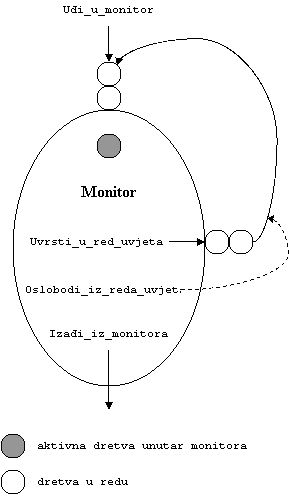
Prve dvije funkcije služe dretvi za ulazak i izlazak iz monitorske funkcije, dok zadnje dvije blokiraju dretvu kada prethodno izračunati uvjeti za nastavak rada nisu ispunjeni, te za oslobađanje jedne dretve iz reda čekanja. Sve osim prve funkcije u ispravnom korištenju moraju se pozvati jedino unutar monitorske funkcije, tj. nakon poziva Uđi_u_monitor(m) kako je to i prikazano na slijedećoj slici.

Iako se monitorske funkcije nazivaju funkcijama one to ne moraju izričito i biti, već to može biti i samo dio programa u jednoj funkciji, za koji vrijedi da je prva naredba ulazak u monitor, a zadnja izlazak iz njega. Funkcija za stavljanje dretve u red čekanja osim blokiranja pozivajuće dretve istovremeno i oslobađa monitor, tj. privremeno izlazi iz monitora, kako bi neka druga dretva mogla ući u monitor i pritom eventualno ispuniti uvjete na koje prva dretva čeka te joj i signalizirati da može nastaviti s radom. Međutim, kako se ne bi dogodilo da tada obje dretve budu unutar monitora, dretva koja je oslobođena iz reda uvjeta ne nastavlja odmah s radom već mora ponovo „ući“ u monitor. U nekom jednostavnijem ostvarenju jezgrina funkcija Uvrsti_u_red_uvjeta mogla bi se sastojati od dva djela. U prvom dijelu se oslobađa monitor i pozivajuća se dretva premješta u zadani red čekanja. Nakon što joj neka druga dretva signalizira da može nastaviti s radom funkcijom Oslobodi_iz_reda_uvjeta, u drugom dijelu funkcije Uvrsti_u_red_uvjeta dretva treba ponovo ući u monitor. Zapravo, u ostvarenju funkcije Oslobodi_iz_reda_uvjeta može se prva dretva iz zadanog reda odmah premjestiti u red u kojem dretve čekaju na ulazak u monitor, a ne u red pripravnih dretvi, pa bi ovaj drugi dio funkcije Uvrsti_u_red_uvjeta bio nepotreban.
Ostali mehanizmi sinkronizacije koje pružaju operacijski sustavi, kao što su to komunikacija porukama, cjevovodima, datotekama i slično neće se razmatrati u ovom radu jer je njihova primarna namjena razmjena podataka među dretvama, a ne sama sinkronizacija.
„Problem pušača cigareta“ predstavio je Patil [3] kako bi ukazao na problem sinkronizacije korištenjem semafora. U ovom radu koristi se isti problem, ali različito rješenje radi ilustracije nekih problema sa semaforima.
U ovom slučaju sustav se sastoji od tri dretve koje predstavljaju pušače te jedne dretve trgovca. Svaki od „pušača“ ima kod sebe u neograničenoj količini jedan od tri sastojka potrebnih da se napravi i zapali cigareta: papir, duhan ili šibice. Svaki pušač ima različiti sastojak, tj. jedan ima samo papir, drugi duhan i treći samo šibice. Trgovac ima sve tri komponente u neograničenim količinama. Trgovac nasumice odabire dvije različite komponente, stavlja ih na stol te signalizira pušačima da su sastojci na stolu. Jedino pušač kojemu nedostaju sastojci stavljeni na stol, smije uzeti oba sastojka, signalizirati trgovcu te potom saviti cigaretu i popušiti ju. Trgovac tada stavlja nova dva sastojka na stol i postupak se ponavlja.
Prilikom rješavanja problema treba prvo uočiti da je postupak stavljanja sastojaka na stol i njihovo uzimanje kritični odsječak kojeg treba zaštititi. Budući samo trgovac stavlja sastojke na stol, problema sa stavljanjem nema, ali bi dretvama pušača trebalo zabraniti da gledaju na stol dok trgovac nešto ne postavi. Kada na stolu nešto ima, pušači bi, u općem slučaju, trebali provjeravati pojedinačno, kako se ne bi dogodilo da istovremeno pokušaju uzeti sastojke sa stola.
Najjednostavnije rješenje je zaštititi svaki sastojak na stolu s jednim binarnim semaforom. Trgovac bi tada nakon postavljanja dva sastojka na stol postavio ta dva semafora i čekao da se stol isprazni. Svaki od pušača čeka na dva sastojka, pa s dva uzastopna poziva funkcije ČekajBSem čeka na dodjelu oba sastojka. Opis dretvi koje simuliraju rad trgovca i pušača prikazan je pseudokôdom u nastavku.
dretva Trgovac() {
ponavljaj {
(s1, s2) = odaberi_dva_različita_sastojka
PostaviBSem(s1)
PostaviBSem(s2)
ČekajBSem(stol)
} do ZAUVIJEK
}
dretva Pušač(p) {
(r1, r2) = sastojci_koje_pušač_nema(p)
ponavljaj {
ČekajBSem(r1)
ČekajBSem(r2)
PostaviBSem(stol)
smotaj_zapali_puši()
} do ZAUVIJEK
}
Već i jednostavnija analiza navedenog koda pokazat će da se u takvom sustavu može dogoditi potpuni zastoj, situacija u kojoj niti jedna dretva ne može nastaviti s radom zbog zahtjeva za nekim sredstvom koji je zauzet od strane neke druge dretve. Naime, može se dogoditi da jedan pušač uzme jedan sastojak, a drugi pušač drugi sastojak, tj. svaki od njih prođe prvi poziv funkcije ČekajBSem(r1), budući za svakog od njih r1 može štititi drugi sastojak. Drugi poziv ČekajBSem(r2) uzrokovat će blokiranje tih dretvi. Trgovac neće staviti nove sastojke jer mu nitko neće signalizirati da je stol prazan te tako svi stoje.
U nekakvom pokušaju popravljanja ovog rješenja moglo bi se dodatnim varijablama označavati stanje stola te bi npr. dretva pušača nakon prolaska jednog semafora (dobivanja jednog sastojka) ažurirala stanje na stolu. Ako bi stol bio prazan tada bi signalizirala dretvi trgovca i prije nego ta dretva ima na raspolaganju oba sastojka. To, međutim, nije rješenje zadanog problema, u kojem se očekuje da nakon što trgovac stavi dva sastojka na stol jedan od pušača zajamčeno može smotati i zapaliti cigaretu.
Rješenje koje koristi samo semafore nije dobro, ako na raspolaganju stoje samo navedene funkcije za rad sa semaforima. Postojanje tog problema je davno uočeno te su ubrzo u jezgru dodane i funkcije koje mogu obaviti nekoliko operacija nad skupom semafora i to nedjeljivo: ako se bilo koja operacija ne može obaviti, neće se obaviti niti jedna. Tako bi se gornji problem riješio kada bi umjesto dva uzastopna poziva funkcije ČekajBSem imali samo jednu funkciju koja bi zauzela oba sredstva odjednom ili niti jedno, ako je samo jedno na raspolaganju.
Uz pretpostavku da jezgrine funkcije koje mogu obavljati više operacija nad skupom semafora nisu dostupne, jedno od mogućih rješenja za zadani problem bila bi dodjela jednog semafora skupu sredstava. Tako bi mogli za svaku kombinaciju sastojaka {(papir, duhan), (papir, šibice), (duhan, šibice)} imati po jedan binarni semafor. Svaki pušač bi čekao na samo jedan binarni semafor, a trgovac bi postavljao samo jedan od tri, ovisno o tome koje je sastojke odabrao i stavio na stol. Ovo je rješenje najprikladnije za zadani problem i ako se želi rješenje za njega tada dalje ne treba tražiti. Međutim, ovo rješenje pretpostavlja da trgovac posjeduje znanje o tome koji semafor povezati s odgovarajućim parom sastojaka. Stvarni problemi koji se rješavaju u praksi raspolažu s više sredstava kod kojih to nije jednostavno ili nije uopće moguće načiniti. Zato je u nastavku traženo drugo rješenje koje bi moglo biti primjenjivo na cijelu klasu sličnih problema.
Slijedeće rješenje pretpostavlja da se osim semafora mogu koristiti i neke pomoćne varijable koje će označavati stanje sredstava (sastojke na stolu). Pomoćne varijable moraju biti u dijelu spremnika koje je dohvatljivo svim dretvama u sustavu (npr. zajednički spremnički prostor za dretve različitih procesa ili globalne varijable za dretve unutar istog procesa). Ideja je da se dretvama pušača jednoj po jednoj omogući uvid u sadržaj stola. Dretva koja na stolu nađe oba sastojka, uzeti će sastojke i signalizirati trgovcu da stavi dva nova sastojka, dok će dretva, koja ne pronađe odgovarajuće sastojke, stol prepustiti drugoj dretvi, a sama ponovno ući u red za pregled stola. Rješenje koje koristi navedena svojstva prikazano je u nastavku.
dretva Trgovac() {
ponavljaj {
(s1, s2) = odaberi_dva_različita_sastojka
stavi_sastojke_na_stol(s1, s2)
PostaviBSem(stol_pun)
ČekajBSem(stol_prazan)
} do ZAUVIJEK
}
dretva Pušač(p) {
(r1, r2) = sastojci_koje_pušač_nema(p)
ponavljaj {
ČekajBSem(stol_pun)
ako (na_stolu_sastojci(r1, r2) = DA ) {
uzmi_sastojke(r1, r2)
PostaviBSem(stol_prazan)
smotaj_zapali_puši()
} inače {
PostaviBSem(stol_pun)
}
} do ZAUVIJEK
}
Pomoćne varijable (koje moraju biti dohvatljive svim dretvama) koriste se u pomoćnim funkcijama te one nisu izravno prisutne u pseudokôdu. Ako su u početnom stanju pri pokretanju dretvi oba binarna semafora neprolazna, trgovac stavlja sastojke na stol, pušači redom provjeravaju sadržaj stola te dretva koja ima treći sastojak uzima sastojke sa stola, signalizira trgovcu, i postupak se ponavlja. Na prvi pogled sve izgleda ispravno. Međutim, zamislimo slijedeći slijed događaja u sustavu:
trgovac stavlja dva sastojka na stol,
jedan pušač uzima sastojke i signalizira trgovcu,
trgovac na stol stavlja opet iste sastojke.
Budući je trgovac i drugi puta stavio iste sastojke na stol, ponovno ih jedino isti pušač može uzeti. Pušač koji je uzeo sastojke potom prelazi u stanje „pušenja“ i u tom stanju može ostati određeno vrijeme (u rješenju nije navedeno koliko dugo). Preostala će dva pušača cijelo to vrijeme naizmjence ispitivati sadržaj stola iako se on neće mijenjati dok god prvi pušač ponovo ne uzme sastojke sa stola. Iako se koriste semafori, u ovom se rješenju u nekim mogućim stanjima sustava pojavljuje takozvano „radno čekanje“. Dretve koje nemaju uvjete za nastavak rada i dalje opterećuju sustav neprestanim provjerama stanja sustava. Iako se takvo stanje javlja rijetko u normalnom radu sustava, takvo rješenje općenito nije prihvatljivo.
Mnogo ozbiljniji problem može nastati ako dretve pušača nemaju isti prioritet, a redovi binarnih semafora su prioritetno organizirani. U takvom se sustavu može dogoditi da upravo pušač s najmanjim prioritetom ima treći sastojak, ali on nikada neće pristupiti stolu jer se druga dva pušača s većim prioritetom u tome izmjenjuju. U takvom slučaju opet govorimo o potpunom zastoju iako se zapravo dvije dretve neprestano izmjenjuju u ispitivanju sadržaja stola, ali niti jedna zapravo ne napreduje.
Rješenje kojim možemo otkloniti gornja dva problema, je da svaki pušač čeka na svom binarnom semaforu, a trgovac pri stavljanju novih sastojaka postavlja sve semafore. Pušač će tada samo jednom pogledati što ima na stolu, dok će u slijedećem pokušaju biti blokiran dok god trgovac ne stavi nove sastojke.
dretva Trgovac() {
ponavljaj {
(s1, s2) = odaberi_dva_različita_sastojka
stavi_sastojke_na_stol(s1, s2)
PostaviBSem(p1)
PostaviBSem(p2)
PostaviBSem(p3)
ČekajBSem(stol_prazan)
} do ZAUVIJEK
}
dretva Pušač(p) {
(r1, r2) = sastojci_koje_pušač_nema(p)
ponavljaj {
ČekajBSem(p)
ako (na_stolu_sastojci(r1, r2) = DA ) {
uzmi_sastojke(r1, r2)
PostaviBSem(stol_prazan)
smotaj_zapali_puši()
}
} do ZAUVIJEK
}
Rješenje je slično već spomenutom kada se za dva sredstva koristi isti semafor. Ipak, razlika je u tome što dretva trgovca ne mora uspostavljati vezu između sastojaka i dretvi pušača već im svima javlja da su novi sastojci na stolu. Pušači pregledavaju sadržaj stola pomoću varijabli koje označavaju stanje na stolu, a ne izravno korištenjem vrijednosti semafora. Zbog toga je ovaj pristup nešto općenitiji i primjenjiviji na više slučajeva. U ovom rješenju se može dogoditi da više pušača istovremeno gleda sadržaj stola, što je za konkretni slučaj i dozvoljeno. Kada to ne bi smjeli raditi bilo bi potrebno koristiti dodatni binarni semafor. Samom konstrukcijom ovo rješenje jako podsjeća na rješenja s monitorima, koji su i napravljeni da rješavaju složene probleme sinkronizacije.
Opći semafori se koriste kao brojila događaja ili slobodnih sredstava. Kod „problema proizvođača i potrošača“ koji komuniciraju preko ograničenog među-spremnika, jedan opći semafor broji prazna mjesta u međuspremniku, a drugi puna. Proizvođač čeka na prvi semafor, tj. na prazno mjesto, a potrošač na drugi semafor, tj. na barem jedno popunjeno mjesto. Početna vrijednost prvog semafora treba odgovarati broju poruka koje stanu u međuspremnik, dok je početna vrijednost drugog semafora nula, jer je u početku međuspremnik prazan.
Drugi problem sinkronizacije koji se često javlja, a koji se rješava općim semaforom, jest problem barijere [5]. Treba sinkronizirati skupinu aktivnosti (dretvi) tako da sve aktivnosti dretvi stignu do odgovarajuće točke prije nego bilo koja od njih ide dalje. Jednostavan primjer za taj problem može biti ukrcavanje skijaša u kabinu žičare. Može se zahtijevati da se kabina pokreće tek kada se napuni do posljednjeg mjesta. Jedan on mogućih rješenja tog problema prikazan je u nastavku.
dretva skijaš () {
ČekajOSem(ulaz)
ČekajBSem(k)
br++
ako je (br < N) {
PostaviBSem(k)
ČekajOSem(prolaz)
ČekajBSem(k)
}
br--
ako je (br > 0) {
PostaviOSem(prolaz)
} inače {
*pokreni kabinu*
za i=1 do N {
PostaviOSem(ulaz)
}
}
PostaviBSem(k)
*vožnja žičarom i silazak na vrhu*
}
Početna vrijednost semafora ulaz treba biti jednaka broju mjesta u kabini, tj. broju N, dok je početna vrijednost semafora prolaz nula. Potencijalni putnici žičarom moraju čekati na prazno mjesto kako bi ušli u kabinu. Vrijednost semafora ulaz je upravo jednaka broju praznih mjesta u kabini. Kada semafor dođe do vrijednosti nule putnici koji već nisu u kabini biti će blokirani na tom semaforu. Svi putnici koji uđu u kabinu, osim zadnjeg, biti će blokirani na semaforu prolaz gdje čekaju da se kabina napuni. Zadnji će putnik, vidjevši da je kabina puna, tj. varijabla br ima vrijednost jednaku N, početi oslobađati ostale putnike iz tog blokiranog stanja. Zadnji će putnik (zadnji koji je ušao u kabinu) samo jednom postaviti semafor prolaz . Putnik kojeg je oslobodio (tj. dretva) oslobodit će slijedećeg i tako sve dok se i zadnji ne oslobodi iz reda. Zadnji putnik oslobođen iz semafora prolaz „pokreće“ kabinu (ili signalizira operateru) te postavlja semafor ulaz na vrijednost N, jer je slijedeća kabina koja dolazi iza trenutne prazna. Predloženo rješenje daje svakom putniku „priliku“ da se upozna sa ostalim putnicima u istoj kabini, prije nego li kabina krene, odnosno prije početka punjenja slijedeće kabine. Ovakva prilika za obavljanje dodatnog posla može biti potrebna u različitim primjenama, a ne samo ovom hipotetskom primjeru. Ako ne postoji takav zahtjev, gornji algoritam se može pojednostaviti tako da zadnja dretva, tj. zadnji putnik koji ulazi u kabinu, pokreće kabinu, otpušta sve dretve u kabini koje čekaju na semaforu prolaz i postavlja semafor ulaz N puta. Binarni semafor k mora se koristiti da bi se spriječilo istovremenu promjenu varijable br .
Ponekad je potrebno semaforu povećati vrijednost za više od jedan. U prikazanom primjeru je to načinjeno korištenjem petlje u kojoj se vrijednost semafora povećava za jedan. Operacijski sustavi uglavnom imaju funkcije kojima je to moguće napraviti i sa samo jednom (jezgrinom) funkcijom. U Win32 okruženju [6] funkcija ReleaseSemaphore prima parametar lReleaseCount koji označava za koliko treba povećati vrijednost semafora. UNIX funkcija semop [7] omogućava istovremeno obavljanje više operacija nad skupom semafora. Svaka se operacija definira pomoću oznake semafora te cijelog broja koji označava operaciju koju treba obaviti. Ako je broj pozitivan, semafor se povećava, ako je negativan semafor se pokuša umanjiti za zadani broj, ali tako da vrijednost ne postane negativna.
U prethodnim primjerima semafori nisu bili dovoljni za sinkronizaciju, već su se koristile i dodatne pomoćne varijable. Što je problem složeniji to je semafor samo instrument ostvarenja osnovne sinkronizacije, dok se dodatne varijable koriste za utvrđivanje mogućnosti nastavka rada dretve. Sinkronizacija monitorom je korak u tom smjeru. Funkcije koje služe za ostvarenje monitora su po svojoj strukturi jednostavne gotovo kao i funkcije semafora, dok su istovremeno upravo građene da budu korištene kao pomoćne funkcije. Nastavak rada ili blokiranje svog rada dretva poduzima na temelju ispitivanja potrebnih uvjeta, a ne stanja monitora. Uostalom, monitor nema uz svoju strukturu podataka nikakvo stanje ili broj. Jedino što se za monitor mora dati razlučiti jest je li trenutno neka dretva unutar monitora ili nije. Upravo će to pokazati primjer rješenja sinkronizacije „problema starog mosta“.
Problem starog mosta [4] sastoji se u tome što treba sinkronizirati dretve koje predstavljaju automobile koji prelaze preko uskog starog mosta kao na sl. 2. Budući je most uzak, u istom trenutku auti ga smiju prelaziti samo u jednom smjeru. Kako je most star, na njemu istovremeno smije biti najviše tri automobila. Za rješenje problema moraju se koristiti dodatne varijable koje će označavati stanje sustava. Potrebno je pratiti u kojem smjeru trenutno voze automobili na mostu te koliko ih trenutno ima na mostu. Svaki automobil, kada želi prijeći preko mosta, mora pogledati ove dvije varijable i zaključiti smije li on na most. Provjera i mijenjanje varijabli stanja sustava je kritični odsječak i mora se zaštititi tako da se obavlja unutar monitora. Rješenje koje je zasnovano na rečenim pravilima prikazano je u nastavku.

dretva automobil () {
smjer = smjer_u_kojem_auto_ide
Kreni_na_most(smjer)
*prijeđi_most*
Siđi_s_mosta(smjer)
}
m-funkcija Kreni_na_most(smjer) {
Uđi_u_monitor(m)
dok je ( auti_most = 3 Ú (smjer ≠ smjer_most Ù auti_most > 0) ){
Uvrsti_u_red_uvjeta(m, smjer)
}
auti_most++
smjer_most = smjer
Izađi_iz_monitora(m)
}
m-funkcija Siđi_s_mosta(smjer) {
Uđi_u_monitor(m)
auti_most--
ako je (auti_most = 0) {
Oslobodi_iz_reda_uvjeta(m, 1-smjer)
Oslobodi_iz_reda_uvjeta(m, 1-smjer)
Oslobodi_iz_reda_uvjeta(m, 1-smjer)
} inače {
Oslobodi_iz_reda_uvjeta(m, smjer)
}
Izađi_iz_monitora(m)
}
Ú
- logička operacija ILI (|| u C-u)
Ù
- logička operacija I (&& u C-u)
Pri silasku auta s mosta potrebno je smanjiti broj automobila na mostu za jedan te potom propustiti slijedeći automobil ili više njih na most. Ukoliko je to bio zadnji automobil na mostu, moguće je da na prelazak mosta s druge strane čeka više automobila, pa im treba omogućiti prilaz mostu i to za najviše do tri takva auta, jer je to kapacitet mosta. Ukoliko automobil nije bio zadnji, propušta se slijedeći auto koji vozi u istom smjeru, ako takav postoji. Funkcija Oslobodi_iz_reda_uvjeta ne mijenja stanje sustava, ako u redu čekanja koji se kao parametar daje funkciji nema dretvi. Zato se ona može pozvati i bez prethodne provjere broja dretvi u tom redu. Uz pretpostavku da varijabla smjer može imati vrijednost 0 ili 1, auti za smjer 0 čekat će u redu uvjeta (m, 0), dok će auti za smjer 1 čekati u redu (m, 1). Varijabla smjer se ne mijenja kada automobil silazi s mosta jer se ona postavlja samo kada automobil prilazi mostu.
Analizom predloženog rješenja može se ustanoviti da se sinkronizacija obavlja ispravno. Ne dopušta se vožnja više od tri automobila na mostu, svi auti na mostu voze u istom smjeru, a kada jedan siđe drugi će moći na most samo ukoliko ide u istom smjeru. Ako automobil ne može na most, on će stati u red uvjeta i neće opterećivati sustav, tj. ne postoji radno čekanje. Također ne postoji situacija koja može izazvati potpuni zastoj.
Međutim, kada bi promatrali kako se sustav ponaša kroz dulje vremensko razdoblje, uvidjeli bi neke moguće neželjene pojave. Moguće je da u nekom trenutku iz smjera u kojem automobili upravo prelaze most dođe navala automobila. Prema predloženom algoritmu, automobili sa suprotne strane neće biti u mogućnosti doći na most dok god automobili iz trenutnog smjera vožnje prelaze most. Budući to u ovom slučaju može potrajati, neki automobili mogu jako dugo čekati na prelazak mosta. Teorijski se čekanje može produžiti u beskonačnost, tj. neki automobili nikada neće preći most. Ovaj problem se naziva „izgladnjivanjem“ po uzoru na istu pojavu kod sinkronizacije pet filozofa [1].
Rješavanje problema izgladnjivanja, tj. uvođenje nekakve pravednosti u raspodjelu raspoloživih sredstava, vrlo je složen problem. Problemu treba oprezno pristupiti kako bi se novim rješenjem, koje će nužno biti složenije, ne izazovu neželjene posljedice, kao što je to potpuni zastoj ili radno čekanje ili pojava stanja u sustavu koje je sinkronizacija trebala onemogućiti.
Za problem starog mosta treba najprije definirati pojam izgladnjivanja, tj. je li ono vremenski ili nekako drukčije određeno. Ako se želi postići da auti ne čekaju više od nekog unaprijed zadanog vremena, treba za svaki dolazak automobila pamtiti vrijeme dolaska, a automobile svrstavati u redove uvjeta organizirane po redu prispijeća. Svaki bi automobil prije pristupa mostu prvo trebao provjeriti prvi auto s druge strane mosta i njegovo vrijeme čekanja te tek ako ustanovi da tamo nema nikoga ili postoji automobil koji može još čekati, može provjeriti ostale uvjete. Ovakvo rješenje s vremenima zahtijevalo bi složenu strukturu podataka (liste) te neće biti dalje razmatrano u ovom radu.
Postoje i jednostavniji načini rješavanja navedenog problema. Moguće je ograničiti ili duljinu reda s jedne strane mosta ili broj automobila koji su prešli preko mosta dok je s druge strane čekao automobil.
Prvi pristup s pokušajem ograničavanja duljine reda s jedne strane mosta u nekim slučajevima neće riješiti problem izgladnjivanja. Tako primjerice auti s one strane mosta na kojoj postoji red kraći od zadanog mogu i dalje beskonačno čekati na prelazak mosta, ako na tu stranu više ne prilaze automobili te se nikada neće dostići granica koja bi automobilima sa suprotne strane spriječila prelazak mosta. S druge strane, ovakav pristup može i dovesti do potpunog zastoja, ako se s obje strane stvori red automobila veći od dozvoljenog.
Drugi pristup, kod kojeg se ograničava broj prelazaka u jednom smjeru dok s druge strane čekaju automobili, jako podsjeća na semafore na križanjima. Oni, istina, rade na vremenskoj osnovi, ali i dalje propuštaju skupinu automobila u jednom smjeru, te potom drugu skupinu u drugom smjeru. Za ostvarenje takve sinkronizacije bit će potrebne dodatne varijable koje će označavati stanje sustava. Za sustav će biti potrebno definirati koliko se automobila u nekom trenutku nalazi sa svake strane, u kojem se smjeru kreću automobili preko mosta te koliko je automobila prošlo preko mosta u tom smjeru dok je s druge strane čekao barem jedan automobil. Svaki će automobil prije prelaska mosta najprije gledati u kojem smjeru se vozi na mostu. Ako se vozi u njegovu smjeru, provjerava postoji li automobil koji čeka na prelazak u suprotnom smjeru i koliko je automobila prešlo preko mosta dok je on čekao. Ako je taj broj manji od neke zadane vrijednosti, tek tada auto može na most u slučaju da se na mostu nalazi manje od tri automobila. U svakom drugom slučaju automobil, tj. dretva kojom ga simuliramo, ulazi u red čekanja. Nakon što je automobil krenuo na most potrebno je provjeriti je li to prvi automobil u tom smjeru jer on u tom slučaju mora brojila prelaska postaviti na nulu. Prilikom silaska s mosta potrebno je povećati broj automobila koji su prešli preko mosta u tom smjeru, ali samo ako s druge strane postoji red. Potom treba ispitati stanje sustava. Ako je to bio zadnji automobil u tom smjeru, tada je potrebno propustiti aute u suprotnom smjeru. Inače treba propustiti slijedeći automobil u istom smjeru. Sve navedeno ugrađeno je u slijedeće rješenje.
dretva automobil () {
smjer = smjer_u_kojem_auto_ide
Kreni_na_most(smjer)
*prijeđi_most*
Siđi_s_mosta(smjer)
}
m-funkcija Kreni_na_most(smjer) {
Uđi_u_monitor(m)
čeka[smjer]++
dok je ((smjer ≠ smjer_most Ù auti_most > 0) Ú prošlo[smjer] > MAX Ú auti_most = 3 ) {
Uvrsti_u_red_uvjeta(m, smjer)
}
auti_most++
ako je (smjer ≠ smjer_most) {
prošlo[1-smjer] = 0
prošlo[smjer] = 0 // ovo zapravo i nije potrebno jer već je u nuli
smjer_most = smjer
}
čeka[smjer]--
Izađi_iz_monitora(m)
}
m-funkcija Siđi_s_mosta(smjer) {
Uđi_u_monitor(m)
auti_most--
ako je (čeka[1-smjer] > 0) {
prošlo[smjer]++
}
ako je (auti_most = 0) {
Oslobodi_iz_reda_uvjeta(m, 1-smjer)
Oslobodi_iz_reda_uvjeta(m, 1-smjer)
Oslobodi_iz_reda_uvjeta(m, 1-smjer)
} inače {
Oslobodi_iz_reda_uvjeta(m, smjer)
}
Izađi_iz_monitora(m)
}
Prikazano rješenje nije znatno složenije od prethodnog i lako je pratiti slijed odlučivanja koje mora napraviti svaki automobil.
Monitor se najčešće koristi za složene slučajeve sinkronizacije gdje se na mnogo lakši i razumljiviji način rješava problem sinkronizacije nego sa semaforima. Jedan od školskih primjera takvih problema je problem pet filozofa [1]. Semafori su u ovom slučaju potpuno neprikladni, dok je rješenje s monitorima vrlo jednostavno i razumljivo.
Problem sinkronizacije sustava dretvi je složen problem. Pri rješavanju problema uvijek treba krenuti od pravila koja se u zadanom sustavu moraju poštivati. Rješavanje problema najčešće je iterativan postupak u kojem se rješenje dobiveno u prethodnom koraku analizira te se poboljšava u slijedećem. Poboljšanja se najčešće odnose na otklanjanje nekih problema uočenih u prethodnom rješenju. Druga poboljšanja mogu biti usmjerena na pojednostavljenje. Jednostavno rješenje je mnogo bolje od složenog jer se takvo rješenje lakše analizira i lakše uočavaju potencijalni problemi. Jednostavno rješenje se uz mnogo manje truda može prilagoditi nekim novim uvjetima.
Za svako od predloženih rješenja u ovom radu dano je podrobno objašnjenje problema koji se mogu pojaviti u sustavu. Problemi na koje je potrebno paziti pri korištenju algoritama sinkronizacije mogu se svrstati u nekoliko kategorija.
Prvo i osnovno, algoritam mora poštivati pravila koja su unaprijed utvrđena za zadani sustav, odnosno, ne smije dopustiti da se sustav nađe u nedozvoljenom stanju.
Drugo, algoritam mora omogućiti normalni rad sustava i ne smije dovesti do stanja potpunog zastoja. Potpuni zastoj može se manifestirati u dva oblika. U prvom su sve dretve blokirane na pozivima jezgrinih funkcija s kojima se sinkronizacija obavlja (npr. semaforima). U ovom se obliku potpuni zastoj javlja u prvom pokušaju sinkronizacije problema pušača cigareta. Drugi oblik dopušta da neke dretve nisu blokirane na tim pozivima, ali se vrte u petlji iz koje ne mogu izaći i nastaviti s korisnim radom.
Treći problem sinkronizacije na koji treba pripaziti jest radno čekanje. Iako se sinkronizacija može obaviti i bez jezgrinih funkcija, one se ipak koriste kako bi se rasteretio sustav. Dretva koja ne može nastaviti s radom treba biti blokirana i prepustiti procesor pripravnim dretvama, a ne u petlji nanovo provjeravati uvjete za nastavak rada. U algoritmima u kojima se koriste jezgrine funkcije može se također pojaviti oblik radnog čekanja, kao što je to pokazano u primjeru „problema pušača cigareta“.
Slijedeći problem na koji treba pripaziti jest problem izgladnjivanja. Problem se manifestira na način da se nekoj dretvi može uskratiti korištenje pojedinog sredstva na neodređeno dugo vrijeme. Uzrok tome mogu biti nove dretve u sustavu koje prilikom zahtjeva za sredstvima pronalaze potrebna sredstva slobodnim. Problem se javlja u sustavima u kojima dretve za nastavak rada trebaju više od jednog sredstva ili je uvjet koji mora biti zadovoljen za nastavak njihova rada sačinjen od nekoliko poduvjeta. Primjer u kojemu se pojavljuje izgladnjivanje je prvo rješenje za „problem starog mosta“. Budući je problem prilično jednostavan, moglo se naći i relativno jednostavno rješenje koje izbjegava izgladnjivanje. U općem slučaju rješavanje problema izgladnjivanja može biti znatno teže te može zahtijevati i dodatne složene podatkovne strukture za prikladno rješenje.
[1] L. Budin, “Operacijski sustavi – predavanja”, 2003.
[2] M. Jones, “What really happened on Mars?”, http://research.microsoft.com/~mbj/Mars_Pathfinder/
[3] D.L. Parnas, “On a Solution to the Cigarette Smoker's Problem,” Comm. of the ACM, Vol 18, No 3, March 1975.
[4] Synchronization Problems, http://inst.eecs.berkeley.edu/~cs162/fa06/handouts/synch-problems.html
[5] http://en.wikipedia.org/wiki/Barrier_(computer_science)
[6] (Win32) Synchronization Functions, http://msdn2.micro-soft.com/en-us/library/ms686360.aspx
[7] (UNIX) Semaphore facility, http://www.opengroup.org/onlinepubs/007908799/xsh/syssem.h.html
[8] (POSIX) threads, http://www.opengroup.org/onlinepubs/-007908799/xsh/pthread.h.html