
Matematička podloga
Matematička podloga
Kao ulazne podatke koristimo 3D modele koji mogu doći iz raznih izvora. Jedina nama bitna razlika između modela istog lica s različitim izrazima jest njihova topologija. Postoji mnogo načina za dobivanje 3D modela ljudskog lica. Većina tih metoda izvlači model iz fotografija i to metodama sličnim kloniranju izraza lica. Rezultati tih metoda su modeli s jednakim topologijama. 3D model možemo dobiti i pomoću 3D uzorkovanja, a onda modeli raznih izraza lica neće imati međusobno odgovarajuće topologije. Budući da je metoda 3D uzorkovanja skupa i ne daje rezultate na razini drugih metoda teško ćemo naići na 3D model istog lica sa različitom topologijom. U slijedećem poglavlju ćemo pokazati metodu interpolacije razasutih točaka za primjenu na modelima sa različitim topologijama.
Primjeri istih modela sa različitim topologijama:


Slika 2.1 3D modeli sa različitim topologijama
Interpolacija na modelu sa različitom topologijom
Za slučaj da ulazni modeli nemaju jednaku topologiju moramo pronaći način realizacije preslikavanja izraza. Najpogodnija metoda za primjenu na takvom problemu je interpolacija razasutih podataka. Da bi tu tehnologiju mogli primijeniti, na 3D modelima lica moramo označiti tzv. karakteristične točke. Karakteristične točke su točke 3D modela koje posjeduju određen značaj u izrazu lica. O broju karakterističnih točaka ovisi kvaliteta interpolacije. Na slici 2.2 vidimo primjer karakterističnih točaka lica.

Slika 2.2 3D model lica sa označenim karakterističnim točkama
Postoji izvorni skup točaka S. U skupu S postoji n<|S| točaka si' za
koje je definirano n vektora pomaka. Te točke ćemo smjestiti u skup S'.
Također postoji ciljni skup točaka T u kojem su sadržane točke pomaknute
u smjeru i za iznos vektora pomaka koji im je pridružen. Cilj nam je dobiti
vektore pomaka za sve ostale točke i to u ovisnosti o zadanim vektorima
pomaka. Takav razmještaj točaka u prostoru je cilj interpolacije razasutih
podataka. Na slici 2.3 vidimo takvu početnu situaciju.
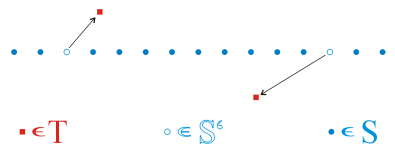
Slika 2.3 Stanje prije interpolacije: Početni vektori pomaka
Točke iz skupa S (plave točke) interpolacijom razasutih točaka želimo porazmjestiti u prostoru tako da ti pomaci budu u ovisnosti o točkama iz skupa T (crvene točke). Bijele točke sa plavim obrubom su točke iz skupa S za koje je definiran vektor pomaka. Rezultat kakav želimo je na slici 2.4.
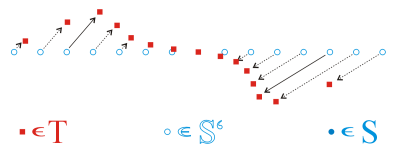
Slika 2.4 Stanje poslije interpolacije: Točke interpolirane u ovisnosti o početnim vektorima pomaka
Kao što se vidi na slici želimo sve točke iz skupa S interpolirati u ovisnosti
o točkama iz skupa T i to tako da rezultat bude optimalan za primjenu
na točkama model ljudske glave.
Funkcija koju želimo dobiti (funkcija koju aproksimiramo) izgleda ovako:
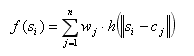 (2.1)
(2.1)
wj su težinski faktori. Oni su nam nepoznati i moramo ih odrediti na temelju
funkcije h(r). h(r) je proizvoljna funkcija i o njoj uvelike ovisi oblik
funkcije f. cj su centri radij-funkcije, u našem slučaju ti centri odgovaraju
točkama iz skupa S'. Postoji mnogo funkcija koje možemo izabrati kao našu
funkciju h(r), ali mi ćemo na temelju rada Ognjena Kosanovića [3] pretpostaviti
da nam najviše odgovara Gaussova funkcija jer je dobro upravljiva konstantom
C, te je prirodnog i glatkog oblika.
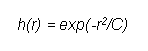 (2.2)
(2.2)
Ako raspišemo funkciju (2.1) dobit ćemo sustav n jednadžbi s n nepoznanica:
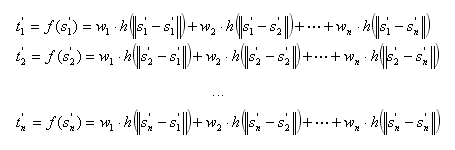 (2.3)
(2.3)
Što u matričnom obliku izgleda ovako:
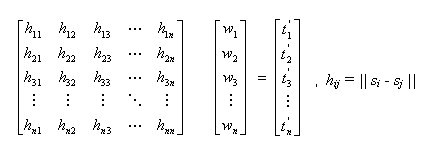 (2.4)
(2.4)
Taj sustav možemo riješiti metodom LUP dekompozicije. LUP dekompozicija
je ustvari L\U dekompozicija s pivotiranjem po stupcima da bi se izbjeglo
dijeljenje s nulom. Ako imamo sustav:
![]() (2.5)
(2.5)
Tada matricu A možemo zamijeniti sa L U:
![]() (2.6)
(2.6)
Sada možemo pisati:
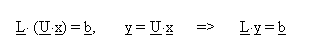 (2.7)
(2.7)
Vektore y
i x dobijamo unaprijednom, odnosno unatražnom supstitucijom:
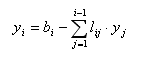 (2.8)
(2.8)
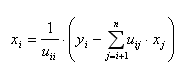 (2.9)
(2.9)
Time smo dobili matematičko oruđe potrebno za rješavanje sustava (2.3),
a time i interpolaciju željenih točaka. Preostaje nam samo u praksi isprobati
kako se promjenom konstante radij funkcije C mijenjaju rezultati interpolacije.
Interpolacija na modelima sa jednakom topologijom
Za interpolaciju
između modela sa jednakom topologijom matematika postaje mnogo jednostavnija.
Svaka točka na izvornom modelu ima svoj odgovarajući par na ciljnom modelu,
što znači da su nam vektori pomaka poznati za svaku točku. Zbog toga možemo
preskočiti metodu interpolacije razasutih podataka iz prošlog poglavlja.
Postoje dva skupa točaka: S kao izvorni i T kao ciljni. Ako želimo preslikati
dio izraza lica sa izvornog na ciljni model najjednostavnije bi bilo samo
preslikati točke dijela lica u ciljni skup točaka.
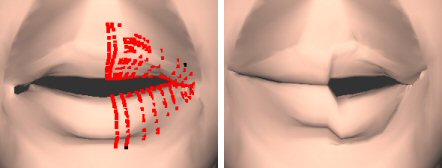
Slika 2.5 Lijevo je model sa označenim točkama, a desno izvorni model sa preslikanim točkama sa lijeve slike
Na slici
2.5 se vidi da takav pristup još nije dovoljno dobar i da moramo uvesti
još neke faktore da bi ciljni skup točaka tvorio model s prirodnim i glatkim
prijelazima. U tu svrhu uvodimo težine za svaku točku izvornog modela
koju preslikavamo. Težina točke određuje utjecaj izvorne točke na preslikanu
točku u ciljnom skupu.
(2.10)
Jednadžbom (2.10) postižemo linearnu interpolaciju između točaka si i ti uz pridodanu težinu vektoru pomaka (ti-si). ti' je interpolirana točka ciljnog modela.
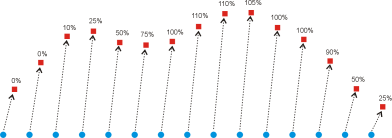
Slika 2.6 Situacija neposredno prije interpolacije: Vektori pomaka sa pripadajućim težinama
Na slici 2.6 vidimo dva skupa točaka. Crvene točke iz skupa S i plave točke iz skupa T. Točkama iz izvornog skupa S su pridružene težine. Težina točke u praksi označava postotak veličine originalnog vektora pomaka. Kada se postavi na više od 100% mogu se dobiti zanimljivi rezultati (slika 3.3, model sa 125% izraza smijeha).
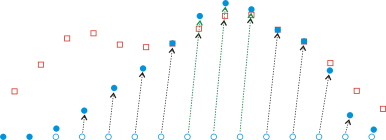
Slika 2.7 Nakon interpolacije: Plave točke iz skupa T pomaknute u smjeru vektora pomaka i uz primjenjene težine na svaki pripadajući vektor
Na slici 2.7 vidimo ciljni skup T (plave točke) nakon interpolacije sa težinama.
Budući da radimo kopiranje izraza sa više izvornih modela istovremeno moguće je označiti više točaka na istom predjelu lica. Za n izvornih modela se zasebno izvodi interpolacija nad označenim točkama i točke koje su interpolirane se stavljaju u listu za svaki model posebno (n lista točaka). Ciljnu sliku na kraju dobijemo kao aritmetičku sredinu svih ekvivalentnih interpoliranih točaka. Pseudokod funkcije za izračunavanje srednje vrijednosti:
deformiranaTočka[][] je polje u kojem su zapisane točke nakon interpolacije, a izvornaTočka[][] je polje sa zapisima točaka izvornih modela. Ako su odgovarajuće točke različite, deformiranu točku dodajemo u sumu iz koje računamo prosjek. ciljnaTočka[] je polje sa zapisom točaka neutralnog modela. Točke u tom zapisu zamjenjujemo sa prosjekom deformiranih točaka, ako deformirane točke postoje. Ako ne postoji deformirana točka ekvivalentna neutralnoj, onda ostaje točka neutralnog izraza.
za i=1 do brojTočaka
{
brojDeformiranih = 0
sumaDeformiranih = 0
za j=1 do brojModela {
ako deformiranaTočka[j,i] <> izvornaTočka[j,i] {
sumaDeformiranih = sumaDeformiranih + točka[j,i]
brojDeformiranih = brojDeformiranih + 1
}
}
ako brojDeformiranih <> 0 {
prosjekDeformiranih = sumaDeformiranih / brojDeformiranih
ciljnaTočka[i] = prosjekDeformiranih
}
}
Određivanje težine točaka u ovom slučaju riješeno je tako da je miš pretvoren u neku vrstu alata za bojanje (slično kao sprej u programima za crtanje). Korisnik mišem označava točke na modelu i to tako da one točke preko kojih se mišem pređe više puta imaju i veću težinu.
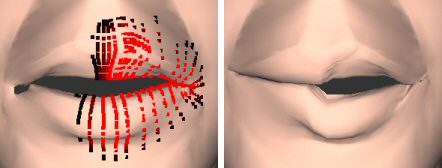
Slika 2.8 Lijevo je model prije interpolacije sa označenim točkama i težinama za svaku točku, a desno je izvorni model nakon primjene interpolacije
Na slici 2.8 se vide rezultati. Iako nisu savršeni, mnogo su bolji nego
na slici 2.5.