4. Ravnina, tijelo

4.1 Jednadžba ravnine

Ravnina je određena s tri nekolinearne točke

Dva su osnovna oblika jednadžbe ravnine: analitički oblik i parametarski oblik jednadžbe ravnine.

4.2 Analitički oblik jednadžbe ravnine

Analitički oblik jednadžbe ravnine je:

(uz h₁ = h₂ = h₃ = 1) vrijedi

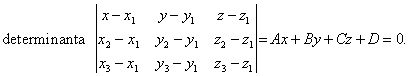(4.1)

Koeficijenti jednadžbe ravnine, u slučaju kada n točaka točno ili približno leži u ravnini, određeni su postupkom

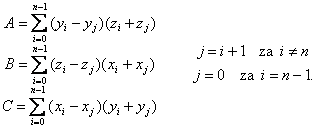, (4.2)

Za i-tu točku s koordinatama (x_i, y_i, z_i) koja leži u ravnini vrijedi:

,

što daje

.

Jednadžbu ravnine R možemo odrediti na osnovi tri točke, odnosno na osnovi tri skalarna produkta

,

odnosno u matričnom obliku:

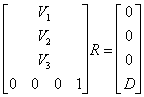
iz čega slijedi

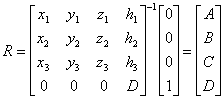(4.3)

gdje su A, B, C koeficijenti vektora normale na ravninu. U slučaju kada su tri promatrane točke kojima želimo odrediti ravninu kolinearne (leže na istom pravcu) rješenje nije jednoznačno. Ako je ravnina određena zadanim točkama koplanarna s ravninama xy, xz, yz, bit će potrebno posebno razmatranje i određivanje vektora normale ravnine (0 0 1), (0 1 0), (1 0 0).

Koeficijente A, B, C vektora normale na ravninu možemo odrediti i kao vektorski produkt dvaju vektora (V₂ - V₁) i vektora (V₃ - V₁):

(4.4)

gdje redoslijed vrhova određuje smjer vektora normale ravnine (prema «gore» ili «dolje»). Ova formula odgovara formuli (4.1).

4.3 Parametarski oblik jednadžbe ravnine

Parametarski oblik jednadžbe ravnine po koordinatama linearna je funkcija dvaju parametara u i w.

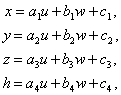(4.5)

Iz 4.5 slijedi matrični oblik

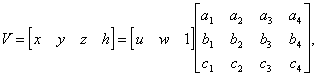(4.6)

odnosno

, (4.7)

gdje je K karakteristična matrica ravnine.

Ako se točkama V₁, V₂ i V₃ pridijeli vrijednost parametara

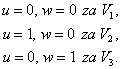
iz 4.6 i 4.7 slijedi

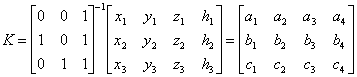(4.8)

4.4 Ispitivanje odnosa točke i ravnine

Skalarni produkt točke i ravnine (slično kao kod pravca i točke) određuje odnos točke i ravnine, pri tome po dogovoru vrijedi:

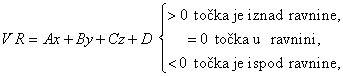(4.9)

4.5 Probodište pravca i ravnine

Probodište je zajednička točka V pravca P i ravnine R,

Na osnovi ova dva uvjeta možemo naći točku u kojoj parametarski zadan pravac probada analitički zadanu ravninu. Odredit ćemo parametar t za koji vrijedi da je točka pravca istovremeno i točka ravnine.

4.6 Zadavanje tijela

Tijelo je zadano geometrijskim i topološkim podacima. Geometrijski podaci su vrhovi, odnosno njihove koordinate. Topološke podatke čini povezanost vrhova, odnosno popisi koji određuju površinu, poligone i bridove, te pripadne vrhove. U ovom primjeru odabrana je organizacija prikazana na slici 4.1. Ovo je jedan od načina organizacije topoloških i geometrijskih podataka, no ovisno o daljnjim postupcima koji će biti načinjeni nad objektom, mogu se koristiti i drugačiji oblici pohranjivanja strukture podataka o objektu.

Trokuti su najčešće korišteni poligoni u opisu tijela zato što je ravnina određena s tri točke. Na primjer, kod tijela koje je zadano četverokutima, sve četiri točke ne leže nužno u ravnini, što može izazvati probleme.

Važno je strukturu podataka načiniti tako da je poznat redoslijed vrhova za pojedini poligon. Redoslijed vrhova možemo odabrati tako da bude u smjeru suprotno kazaljke na satu gledano izvan tijela. Redoslijed vrhova određuje orijentaciju normala poligona. Za neko tijelo normale svih poligona moraju biti usmjerene na isti način, na primjer sve u unutrašnjost tijela ili sve izvan tijela.

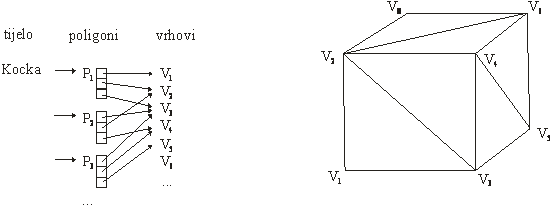
Slika 4.1. Tijelo i pripadna struktura podataka.

Tijelo se može sastojati i od površina različite boje. U tom slučaju se poligoni grupiraju u skupine istih svojstava.

Za primjer na slici 4.1. popis vrhova, tako da je redoslijed vrhova poligona u smjeru suprotno kazaljke na satu gledano izvan tijela, izgledao bi ovako:

Kocka: Podaci u datoteci za vrhove i poligone:

P₁ V₀ V₁ V₂ v 0.0 0.0 0.0 f 1 3 2

P₂ V₂ V₁ V₃ v 0.0 0.0 1.0 f 3 4 2

P₃ V₂ V₃ V₄ v 1.0 0.0 0.0 f 3 5 4

P₄ V₄ V₃ V₅ v 1.0 0.0 1.0 f 5 6 4

P₅ V₄ V₅ V₆ v 1.0 1.0 0.0 f 5 7 6

P₆ V₆ V₅ V₇ v 1.0 1.0 1.0 f 7 8 6

P₇ V₆ V₇ V₀ v 0.0 1.0 0.0 f 7 1 8

P₈ V₀ V₇ V₁ v 0.0 1.0 1.0 f 1 2 8

P₉ V₀ V₂ V₄ # komentar f 1 5 3

P₁₀ V₀ V₄ V₇ f 1 7 5

P₁₁ V₁ V₅ V₃ f 2 4 6

P₁₂ V₁ V₇ V₅ f 2 6 8

4.7 Orijentacija normale ravnine

Vektor normale n ravnine R može biti usmjeren

- u unutrašnjost tijela,

- izvan tijela.

Tri susjedna nekolinearna vrha V_i-1, V_i, V_i+1 u popisu vrhova poligona određuju koeficijente jednadžbe ravnine R,

(4.10)

a time i komponente vektora normale n na ravninu R

. (4.11)

Uz pretpostavke:

- redoslijed vrhova V_i-1, V_i, V_i+1 je u smjeru suprotno kazaljke na satu gledano izvan tijela

- srednji vrh je na konveksnom dijelu poligona (za trokute uvijek ispunjeno)

vektor normale n ravnine R usmjeren je izvan tijela.

4.8 Ispitivanje odnosa točke i konveksnog tijela

U slučaju kada se radi o konveksnom tijelu, te kada je vektor normale ravnine usmjeren izvan tijela, točka V je unutar tijela ako vrijedi

(4.12)

odnosno, točka V je izvan tijela ako vrijedi

(4.13)

Ako je tijelo konkavno tada se iz točke povlači zraka i određuje probodište zrake i stranice tijela. Ako je broj probodišta

- paran, točka je izvan tijela,

- neparan, točka je unutar tijela.

4.9 Zapisi poligonalnih objekata

Zapisivanje trodimenzijskih objekata obično je propisano specifikacijama proizvođača programske opreme. To su, na primjer, zapisi s ekstenzijom .3ds, .max, .dxf, .ply, .obj, .xgl, .stl, .wrl, .iges … . Ovisno o zapisu, zapisani mogu biti trokuti ili poligoni s više vrhova, grupe poligona, boje, teksture, normale u poligonima ili vrhovima, krivulje, površine, način konstrukcije objekata, podaci o sceni, izvori svjetla, podaci o animaciji i slično. U vježbi će biti korišten zapis .obj, odnosno dio tog zapisa.

4.10 Radni zadatak

Zadan je jednostavan primjer u kojem se koristi samo dio zapisa objekta Wavefront (.obj). Zapis sadrži popis vrhova i njihovih koordinata te popis poligona s pripadnim indeksima vrhova.

1. Iz datoteke učitati zadano tijelo (za primjer sa slike 4.1)

- u prvom prolazu izbrojiti broj vrhova i poligona (prvo slovo v, f ili #)

- načiniti alokaciju potrebnog memorijskog prostora

- učitati geometrijske i topološke podatke (vrhove i poligone)

- zadati koordinate ispitne točke V.

2. Odrediti A_i, B_i, C_i, D_i koeficijente jednadžbe ravnine, za svaki poligon tijela. Koristiti formulu 4.1. odnosno:

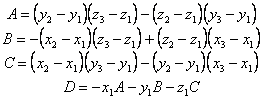
3. Za ispitnu točku V odrediti da li je unutar ili izvan konveksnog tijela. Koristiti uvjete 4.12, 4.13.