EO radno okruženje

2.1. Što su genetski algoritmi

Genetski algoritmi su heuristička metoda traženja rješenja. To znači da neće prvo rješenje koje će dati biti točno, nego će procjenjivati moguća rješenja te na temelju procjene odabrati ono najbolje. Da bi generirao moguća rješenja algoritam koristi evolucijske tehnike koje se susreću i u prirodi (selekcija, mutacija, križanje).
Rad genetskog algoritma može se jednostavno predočiti slikom :

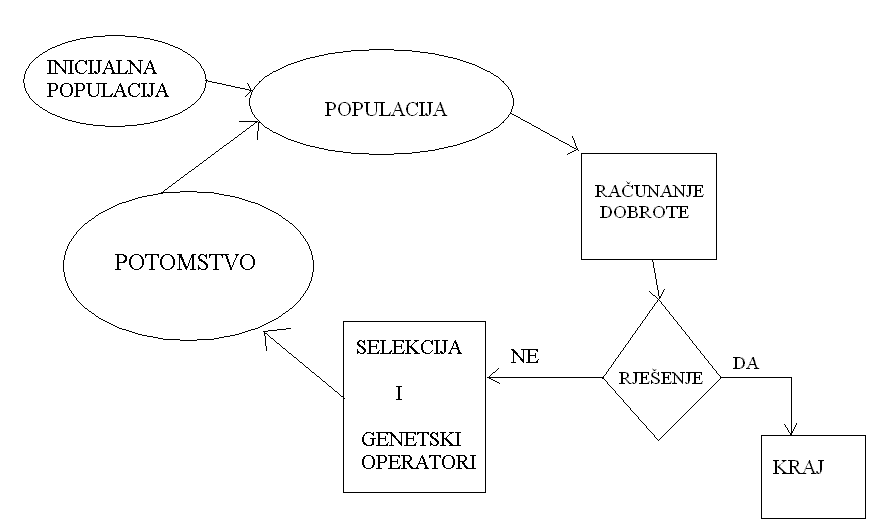
slika 1. rad genetskog algoritma

Kao što se vidi algoritam iz populacije traži rješenje računajući dobrotu jedinke. Ako niti jedna jedinka nije dovoljno dobra , tada se nad populacijom obavljaju genetski operatori i selekcija koji će genrirati novu populaciju.

2.2. Jedinka i populacija

U računalu možemo jedinku predstaviti kao niz bitova , niz cijelih ili realnih brojeva.Jedinke predstavljaju moguća rješenja zadanog problema.

Populacija je skup svih jedinki. Najčešće je tijekom izvođenja genetskog algoritma veličina populacije konstantna. Inicijalna populacija je prva populacija tj. populacija s kojom genetski algoritam počinje rad. Ona je najčešće slučajno generirana.

2.3. Funkcija dobrote

Najvažniji dio genetskih algoritama je funkcija dobrote (funkcija cilja), jer predstavlja ključ selekcije (određuje koje se jedinke odbacuju , a koje ostaju u populaciji) te također predstavlja sami problem koji se rješava. Zadatak funkcije dobrote je odrediti koliko je dobra pojedina jedinka. Što će dobrota biti veća to će jedinka imati veću vjerojatnost preživljavanja. Jedinke s manjom vrijednošću dobrote imati će manju vjerojatnost preživljavanja. Vjerojatnost će biti različita od 0 jer je time omogućeno da se algoritam ne zaustavi u nekom lokalnom maksimumu.

2.4. Unarni operatori (mutacija)

Mutacija je operator koji djeluje nad jednom jedinkom i kao rezultat daje izmijenjenu jedinku. Svrha mutacije je da ubaci novi genetski ''materijal'' u populaciju i tako onemogući zaustavljanje u prvom lokalnom optimumu koji se nađe. Vjerojatnost mutacije se postavlja na vrlo malu vrijednost (npr. 0.01) jer bi se u suprotnom genetski algoritam pretvorio u algoritam slučajne pretrage prostora rješenja. Postoji više vrsta mutacija ovisno o tipu jedinke nad kojom se mogu izvršavaju

Mutacija nad bitovima (jednostavna mutacija) :
Izvršava se nad jedinkom koja ima binarni prikaz. Parametar mutacije je vjerojatnost (p) da se određeni bit promijeni.

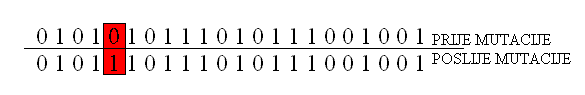
slika 2. jednostavna mutacija

Mutacija nad realnim brojevima :
Kada se bi jednostavna mutacija primjenjivala na jedinku koja je predstavljena kao realna vrijednost promjena jednog bita mogla bi dovesti do vrlo velike promjene vrijednosti jedinke. Budući da jedinka nosi informaciju kao realni broj takav slučaj nam nije koristan

Uniformna mutacija :

Pretpostavimo da je jedinka definirana kao niz realnih brojeva . Primjenom uniformne mutacije jedinka će prijeći u gdje su x_i i y_i elementi iz . Element y_i je uniformno izabran iz danog intervala tj. vjerojatnost biranja bilo kojeg broja iz tog intervala je konstantna.

Normalna mutacija :

Normalna mutacija je slična uniformnoj ali , biranje broja iz intervala ne podliježe uniformnoj razdiobi , nego normalnoj (Gaussovoj ) razdiobi pa je tako vjerojatnost pojavljivanja broja bliže rubu manja od ong bliže centru.

Mutacije nad permutacijama :

Ponekad je jedinka predstavljena kao permutacija određenog niza brojeva. Primjenom neke od gornje navedenih mutacija bi moglo uništiti to svojstvo (recimo dobijemo broj koji ne pripada zadanom nizu) pa ćemo definirati novu mutaciju

Swap (miješajuća) mutacija :
Ta mutacija je vrlo jednostavna i kao parametar ima broj zamjena u kromosomu :

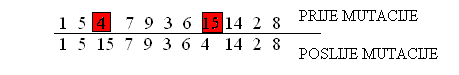
slika 3. miješajuća mutacija

2.5. Binarni operatori(križanje)

Križanje s jednom točkom prekida
Križanje s jednom točkom prekida je najjednostavniji oblik križanja. Uzimaju se dva roditelja te križanjem nastaje jedano ili dvoje djece. Algoritam križanja radi na vrlo jednostavnom principu : izabire se broj između [0, b-1] (b – broj bitova) te se na tom mjestu zamijene repovi roditelja ( rep – niz bitova desno od izabranog mjesta ).

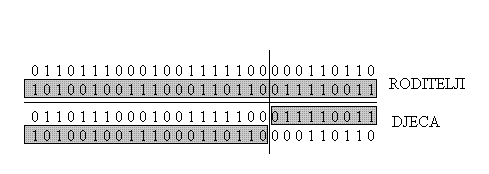
slika 4. križanje s jednom točkom prekida

Križanje s N točaka prekida
Križanje s N točaka prekida je prošireno križanje s jednom točkom prekida. Umjesto jedne točke izabire s N točaka .

Uniformno križanje
Uniformno križanje je križanje s b-1 točaka prekida. Vjerojatnost da dijete naslijedi svojstvo roditelja je 50 % (p=0.5).Također je moguće definirati poseban vektor koji će sadržavati za svaki bit posebnu vjerojatnost. Takava vrsta križanja se naziva p-uniformno križanje. U ovom slučaju nam vjerojatnost p ( koja može biti različita za pojedine bitove) govori kolika je vjerojatnost da bude nasljeđen bit od prvog roditelja.Ako prilikom križanja nastaju dva djeteta tada drugo djete nastaje na suprotan način od prvog (ovdje se ne može reći da je drugo dijete negacija prvog jer ako oba roditelja imaju isti bit tada će i djeca na tom mjestu imati isti bit ).

Segmentno križanje
Segmentno križanje je križanje kod kojeg se slučajno bira broj točaka i mjesto prekida .

2.6. Selekcija

Uloga selekcije u algoritmu je da sačuva dobre jedinke unutar populacije (i omogući operatorima da stvore još bolje) i da odbaci loše jedinke.

Jednostavna selekcija
Selekcija pojedine jedinke ovisi o njenoj dobroti tj. koliko je dobra pojedina jedinka u usporedbi s cijelom populacijom

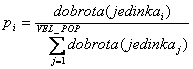
Nedostatci:
Ako postoje jedinke koje su puno bolje od ostatka , može se desiti da će preuzeti cijelu populaciju (prerana konvergencija ).
Kad sve jedinke imaju približno jednaku dobrotu selekcija se pretvara u uniformnu selekciju i dobrota u tom slučaju nema veliki značaj.
Ako je potrebno normalizirati dobrotu jedinki tada će se promijeniti vrijednosti vjerojatnosti svih jedinki i više neće biti isti uvjeti selekcije kao prije.

Turnirska selekcija
Parametar turnirske selekcije je broj k ( k>2) . Radi tako da iz populacije uzima slučajno k jedinki i od njih bira najbolju te ju seli u novu populaciju gdje će se vršiti genetski operatori . Selekciju određuje i vjerojatnost (p) da najbolja jedinka bude izabrana. Ako je p = 1 tada govorimo o determinističkoj turnirskoj selekciji , a ako je p < 1 tada govorimo o stohastičkoj turnirskoj selekciji.

Random selekcija
Turnirska selekcija s vrijednošću k=1 se pretvara u slučajnu selekciju. Takav tip selekcije daje najlošije rezultate i uglavnom se ne koristi.

2.7. Uvjet završetka

Uvjet završetka definira kraj izvođenja genetskog algoritma. Uvjet je najčešće maksimalan broj generacija koje algoritam smije dostići, no radi optimizacije izvođenja mogući su i drugačiji uvjeti , npr. kad dobrota jedinke dostigne određenu razinu ili kada ne dolazi do promjene u populaciji nakon nekoliko generacija.