Sadržaj

Program
Novosti u odnosu na verziju 1.0
Novosti u odnosu na verziju 1.1
Novosti u odnosu na verziju 1.2
Opis rada programa

Primjer1
Primjer2
Primjer3
Primjer4

Binarni operatori
Unarni operatori
Skraćeni unarni operatori
Ternarni
Logički operatori
Operatori komparacije

Program

Program je dostupan na ovom linku .

Novosti u odnosu na verziju 1.0

Uklonjen je glavni nedostatak programa te se sada može odjednom generirati više grafičkih prikaza. Postoji naredba (Drawing) koja stvara novu površinu za crtanje, i u kojoj se mogu raditi animacije i sl, neovisno o ostalim površinama za crtanje! Dodana je podrška za neizrazito upravljanje (FuzzyControlSystem). Napravljene su manje izmjene u dizajnu osnovnog prozora programa. Promijenjena je sintaksa DrawFunc naredbe, i uvedeno je grupiranje naredbi u blokove.

Novosti u odnosu na verziju 1.1

Dodano je još nekoliko novih funkcija, te je ispravljen bug koji se je provlačio od početka a odnosi se na neispravan prikaz crteža prilikom promjene dimenzija prozora. Od sada se ponovno iscrtavanje prozora može pokrenuti pritiskom na DESNU tipku miša bilo gdje u prozoru. Poboljšana je dojava pogrešaka. Sada se do opisa pogreške može doći pritiskom na gumb Pogreške (povratak na kod dobije se ponovnim pritiskom istog gumba).

Novosti u odnosu na verziju 1.2

Uvedena je podrška za zadavanje i treniranje percpetrona (Perceptron naredba) kao i podrška za zadavanje i treniranje višeslojnog perceptrona (MultiLayerPerceptron naredba) a ujedno i omogućeno automatsko kreiranje C source koda koji oponaša i trenira dotičnu mrežu perceptrona. Applet se učitava na donekle izmjenjen način tako da bi sada trebala funkcionirati i podrška za Java Swing tehnologiju što bi trebalo rezultirati iskorištavanjem naprednih mogučnosti koje FSIT nudi.

Opis rada programa

Program je namijenjen vizualizaciji osnovnih operacija sa neizrazitim skupovima, te animaciji utjecaja parametara na često korištene parametrarske norme. Program omogućava definiranje domena, neizrazitih skupova nad tim domenama, te kontrolu animacije, parametara i sl. Program je pisan u Javi, pa poruke o eventualnim pogreškama ispisuje na Java Console.

Evo jednostavnog primjera programa koji će demonstrirati neke mogućnosti. Program daje animirani prikaz djelovanja Hamacherove S norme (koja spada u parametrizirane binarne norme) na neizraziti skup koji je definiran trapeznom funkcijom pripadnosti (s parametrima [5,11,19,25]) te na neizraziti skup koji je definiran trokutastom funkcijom pripadnosti (s parametrima [15,25,35]) pri čemu se parametar Hamacherove S norme mijenja u rasponu od [0,10] u 30 koraka. Istovremeno je prikazano i djelovanje Hamacherove T norme na ista dva neizrazita skupa, ali uz jedan fiksiran parametar. Sve naredbe koje se koriste biti će objašnjene u nastavku, a potpun popis i način uporabe svih naredbi nalazi se u poglavlju POPIS NAREDBI I OPERATORA .

Program se upiše u polje za upis programa (može se koristiti i COPY/PASTE gornjeg primjera), i pritisne se gumb Obradi.

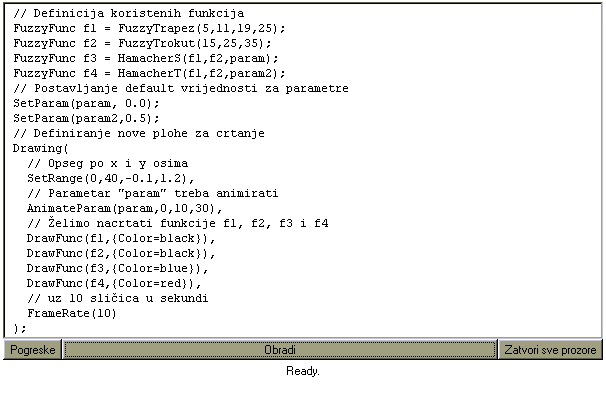
Rezultat je novi prozor u kojem je prikazana animacija:

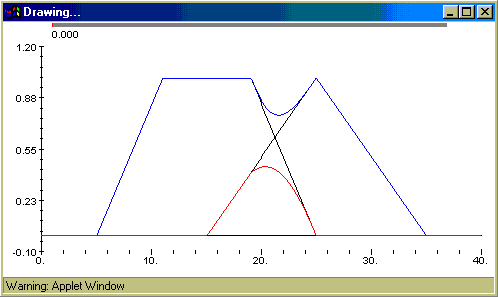
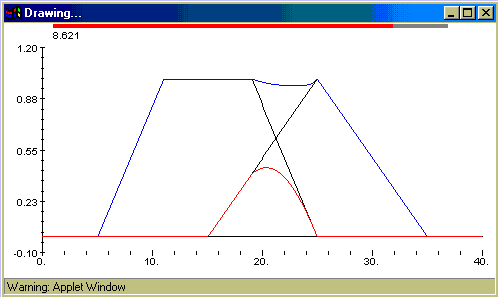
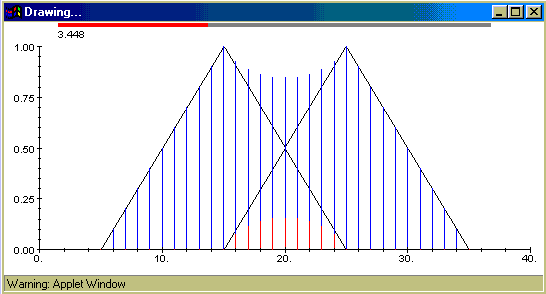
Uočite da je plavom bojom nacrtana funkcija koja se mijenja u ovisnosti o parametru. Pogledajmo jedan od ovih prikaza u malo krupnijem planu:

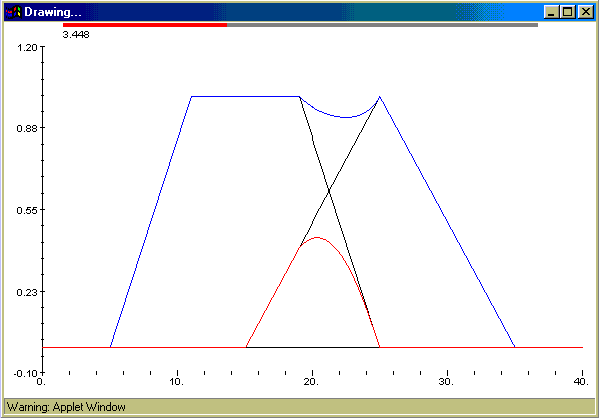
Slika se sastoji od jednog trapezoida (crno), jedne trokutaste funkcije (crno), njihove Hamacher unije (plavo) te njihovog Hamacher presjeka (crveno). Također su nacrtani pravci x=0 i y=0 (osi koordinatnog sustava). Na vrhu slike nalazi se indikator vrijednosti parametra (grafički i numerički). Pogledajmo sada koje su naredbe prethodnog programa odgovorne za ovakav prikaz.
Trapezoidna funkcija nastala je kao rezultat naredbe:

FuzzyFunc f1 = FuzzyTrapez(5,11,19,25);

Ovom naredbom definira se nova funkcija f1 koja predstavlja instancu trapezoidne funkcije. Sve definicije funkcija kojima se stvaraju funkcije pripadnosti započinju ključnom riječi FuzzyFunc, zatim slijedi jedinstveni naziv nove funkcije pa znak jednakosti, nakon čega dolazi izraz koji definira funkciju. Sada može doći definicija domene (ali nije nužno) na što ćemo se osvrnuti kasnije. Konačno mora doći točka-zarez koja završava definiciju.

Trokutasta funkcija također je rezultat slične naredbe koja se pokorava upravo opisanim pravilima:

FuzzyFunc f2 = FuzzyTrokut(15,25,35);

Ovime je stvorena funkcija f2 koja je jedna konkretna instanca trokutaste funkcije.

Program nadalje definira dvije nove funkcije f3 i f4 koje su rezultat spajanja funkcija f1 i f2 jednom od Hamacher normi za zadanim parametrom:

FuzzyFunc f3 = HamacherS(f1,f2,param);
FuzzyFunc f4 = HamacherT(f1,f2,param2);

Uočite da funkcija f3 koristi Hamacher S normu sa parametrom koji smo nazvali param, dok funkcija f4 koristi Hamacher T normu sa parametrom koji smo nazvali param2. Mogli smo obje funkcije napraviti ovisne o istom parametru (npr. param ), ali za potrebe primjera ovo smo namjerno razdvojili u dva parametra.

U programu sada slijedi naredba:

SetParam(param, 0.0);
SetParam(param2,0.5);

Svrha ovih naredbi je da parametar param veže na fiksnu zadanu vrijednost 0.0, a param2 veže na fiksnu zadanu vrijednost 0.5. Ovo će za posljedicu imati da sve funkcije koje su bile ovisne o parametru imenovanom nazivom param odnosno param2 sada koriste te zadanu vrijednost (osim ukoliko se ovo ne poništi drugom SetParam naredbom u nekom bloku). Kod nas se to odnosi na funkcije f3 i f4 koje će sada raditi uniju funkcija f1 i f2 Hamacher normom sa parametrom 0.0, odnosno presjek funkcija f1 i f2 Hamacher normom sa parametrom 0.5. Svi parametri moraju biti postavljeni na svoje default vrijednosti (dakle, za svaki parametar mora biti pozvana SetParam naredba izvan svih blokova; pojam bloka objašnjen je kasnije).

U programu dalje slijedi definicija jedne plohe za crtanje. Ovo se definira Drawing blokom. Opći oblik je:

Drawing(
...
);

Ova naredba definira jedan blok naredbi. Unutar bloka naredbe se odvajaju zarezom (a ne točka-zarezom). Unutar bloka dozvoljeno je pozvati naredbu SetParam i nanovo definirati vrijednost nekog parametra čime će se poništiti stara definicija. Isto tako unutar bloka dozvoljena je uporaba i novih naredbi koje se ne smiju koristiti izvan blokova: AnimateParam, SetRange , DrawFunc, SetTitle i FrameRate.

Naredbom:

SetRange(0,40,-0.1,1.2),

postavlja se raspon "prozora" koji će se iscrtavati. Ovime naređujemo iscrtavanje po x koordinati od 0 do 40, te po y koordinati od -0.1 do 1.2.

Slijedi naredba koja prikazu dodaje dinamiku:

AnimateParam(param,0,10,30),

Ova naredba rezultira animiranjem parametra param u rasponu od 0 do 10 u 30 koraka. Parametru se redom pridružuju vrijednosti iz linearno rastućeg niza od donje zadane granice do gornje zadane granice, te se vrši iscrtavanje zadanih funkcija, što rezultira animacijom (uočite da je u izvan svih blokova ovaj parametar postavljen na fiksnu vrijednost 0.0). Sada se može do kraja definirati uporaba parametara:

"Svi parametri koji su korišteni tijekom definicija funkcija moraju biti postavljeni na neku fiksnu vrijednost (SetParam) izvan svih blokova. Unutar Drawing bloka ti parametri mogu biti ili animirani (AnimateParam, i to samo jedan) ili postavljeni na neku novu fiksnu vrijednost uporabom funkcije SetParam, ukoliko se ne želi koristiti default vrijednost parametra. "

Inicijalno u programu oba su parametra fiksirana. U bloku za crtanje parametar param animiramo funkcijom AnimateParam a parametru param2 ostavljamo fiksnu vrijednosti koju se naslijedio iz SetParam poziva koji se nalazi izvan ovog bloka. Ovako napisan program rezultirao je animacijom funkcije f3 (jer ona koristi param), i statičnom funkcijom f4 (jer ona koristi param2 koji je fiksiran). Da smo funkcije f3 i f4 načinili ovisne o istom parametru (param ), tada bi obje funkcije bile animirane istovremeno!

Slijede naredbe koje definiraju koje će se funkcije iscrtavati, i kojom bojom:

DrawFunc(f1,{Color=black}),
DrawFunc(f2,{Color=black}),
DrawFunc(f3,{Color=blue}),
DrawFunc(f4,{Color=red}),

DrawFunc prima dva parametra: funkciju koju treba iscrtati, i skup opcija koje se primjenjuju na iscrtavanje te funkcije. Ovaj drugi parametar je opcionalan. Za sada podržane opcije su Color=naziv i PlotJoined=true ili false. Pojedine opcije odvajaju se zarezima, a značenje će biti navedeno u nastavku.

Poslijednja naredba programa je naredba kojom se definira koliko sličica u sekundi želimo:

FrameRate(10)

Ovime smo definirali da želimo 10 sličica u sekundi. Naravno, ovu naredbu treba uzeti sa rezervom. Naime, naredba postavlja "željeni" broj sličica u sekundi. No ukoliko iscrtavanje jedne sličice traje 500 ms, očito je da je nemoguće u jednoj sekundi iscrtati deset sličica. Stoga ovu naredbu treba shvatiti kao postavljanje gornje ograde, a ne stvarnih vrijednosti.

Pogledajmo sada sljedeći primjer.

FuzzyUniverse un1 = integer discrete {5,35,1}; FuzzyFunc f01 = FuzzyTrokut(5,15,25); FuzzyFunc f02 = FuzzyTrokut(15,25,35); FuzzyFunc f1 = FuzzyTrokut(5,15,25) @ un1; FuzzyFunc f2 = FuzzyTrokut(15,25,35) @ un1; FuzzyFunc f3 = HamacherS(f1,f2,param); FuzzyFunc f4 = HamacherT(f1,f2,param); SetParam(param,0.0); Drawing ( AnimateParam(param,0,10,30), DrawFunc(f01,{Color=black}), DrawFunc(f02,{Color=black}), DrawFunc(f3,{Color=blue}), DrawFunc(f4,{Color=red}), SetRange(0,40,0.0,1.0), FrameRate(10) );

Rezultat pokretanja primjera je prozor sa slijedećom animacijom:

Što se je sada dogodilo? Pogledamo li u program, uočiti ćemo jednu novu naredbu, i modifikaciju FuzzyFunc naredbe. Nova naredba je:

FuzzyUniverse un1 = integer discrete {5,35,1};

koja definira domenu pod nazivom un1, i to na slijedeći način: domeni un1 pripadaju svi cijeli brojevi između 5 i 35 (uključivo ili), i to počev od donje granice (5) sa korakom 1. Dakle, domena je definirana kao skup brojeva {5,5+1=6, 6+1=7, ..., 35}. Više o definicijama domena biti će riječi u nastavku.

Funkcije f1 i f2 definirane su nad domenom un1:

FuzzyFunc f1 = FuzzyTrokut(5,15,25) @ un1;
FuzzyFunc f2 = FuzzyTrokut(15,25,35) @ un1;

Dakle, kada želimo definirati domenu neke funkcije, tada u nastavku treba dodati @ ("AT") pa naziv skupa koji je prethodno definiran, ili se sada može direktno definirati domena. Npr. ispravno je i ovo:

FuzzyFunc f1 = FuzzyTrokut(5,15,25) @ integer discrete {5,35,1};

Gornji primjer je čak i spretniji ako definirate samo jednu funkciju.

Sve ostale naredbe programa poznate su otprije. Ovdje treba naglasiti dvije važne stvari:

• Ukoliko domenu ne definirate eksplicitno, tada se ta domenu automatski uzima skup realnih brojeva (beskonačan skup od minus do plus beskonačno).
• Ukoliko stvarate neki izraz koji koristi funkcije sa već definiranim domenama, tada stvoren izraz automatski nasljeđuje domenu.

FuzzyFunc f3 = HamacherS(f1,f2,param);
FuzzyFunc f4 = HamacherT(f1,f2,param);

Naime, iako f3 i f4 ne definiraju domene eksplicitno, one preuzimaju domene od podređenih funkcija f1 i f2, pa su tako i f3 i f4 definirane nad istim skupom un1.

Evo još jednom primjera:

FuzzyUniverse un1 = integer discrete {10,30,1}; FuzzyFunc f1 = Which( <=(x,10),0, &&(>(x,10),<=(x,20)),*(-(x,10),0.1), &&(>(x,20),<=(x,30)),-(1,*(-(x,20),0.1)), default,0 ) @ un1; Drawing ( DrawFunc(f1,{Color=black}), SetRange(0,40,0.0,1.0), FrameRate(10) );

Ovaj primjer donosi nam mnoštvo novosti. Radi lakše čitljivosti primjera, odmah treba napomenuti da su sve operacije implementirane kao funkcije, te koriste prefiks notaciju. Evo što je novoga. Funkcija f1 definira se po dijelovima ključnom riječi Which. Sintaksa je slijedeća: Which(uvjet1, izraz1, uvjet2, izraz2, ... ). Sve funkcije koje se definiraju ključnom riječi FuzzyFunc implicitno su funkcije jedne varijable; pristup do te varijable dobiva se pod imenom x. Pogledajmo sada što je zapravo definirano izrazom:

Which(
<=(x,10),0,
&&(>(x,10),<=(x,20)),*(-(x,10),0.1),
&&(>(x,20),<=(x,30)),-(1,*(-(x,20),0.1)),
default,0
)

tako da to prepišemo u malo intuitivniji infix oblik (napomena: ovo što slijedi nije ispravan program!):

Which(
IF( x <= 10 ) THEN RETURN 0;
ELSE IF( (x > 10) AND (x<=20) ) THEN RETURN (x-10)*0.1;
ELSE IF( (x > 20) AND (x<=30) ) THEN RETURN 1-((x-20)*0.1);
ELSE RETURN 0;
)

Dakle, početni izraz definira trokutastu funkciju:

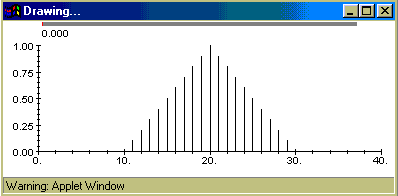
Prikaz funkcije je diskretiziran jer je u programu funkcija definirana nad diskretnim skupom. U funkciji Which uvjeti se ispituju slijedno, i funkcija će vratiti prvi izraz za koji je uvjet zadovoljen. Što se događa ukoliko uvjeti koji nas zanimaju nisu ispunjeni može se zadati ključnom riječi default , kao u prethodnom programu. No ovo znači da ako kao prvi uvjet stavite default, taj uvjet je uvjek ispunjen i funkcija će uvijek vratiti pripadajući izraz, te se ostali uvjeti koji su navedeni iza uopće neće ispitivati!

Evo odmah prilike da pogledamo što znači opcija PlotJoined=true DrawFunc naredbe. Uzmimo isti primjer kao i prethodni, i dodajmo novi blok za iscrtavanje koji ima modificirani poziv DrawFunc naredbe:

FuzzyUniverse un1 = integer discrete {10,30,1}; FuzzyFunc f1 = Which( <=(x,10),0, &&(>(x,10),<=(x,20)),*(-(x,10),0.1), &&(>(x,20),<=(x,30)),-(1,*(-(x,20),0.1)), default,0 ) @ un1; Drawing ( DrawFunc(f1,{Color=black}), SetRange(0,40,0.0,1.0), FrameRate(10), SetTitle("DrawFunc sa PlotJoined=false (default)") ); Drawing ( DrawFunc(f1,{Color=black,PlotJoined=true}), SetRange(0,40,0.0,1.0), FrameRate(10), SetTitle("DrawFunc sa PlotJoined=true") );

Rezultat je:

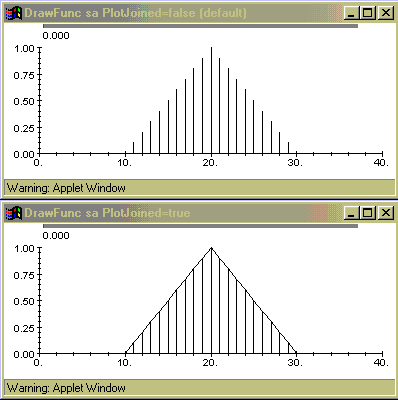
Prvi Drawing blok rezultirao je očekivanom slikom. Drugi Drawing blok zbog PlotJoined=true opcije prikazao je funkciju kao da je kontinuirana, zadržavajući pri tome i njezin diskretni prikaz.

Primjer 4.

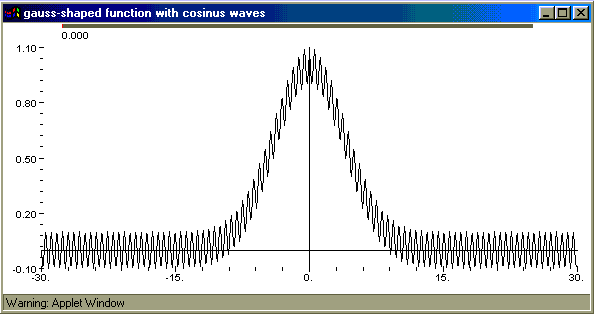
U nastavku je dan jedan jednostavan primjer koji pokazuje rad sa aritmetičkim funkcijama.

FuzzyFunc f = +(GaussShaped(x,0,4),*(0.1,Cos(*(x,10)))); Drawing( SetTitle("gauss-shaped function with cosinus waves"), SetRange(-30,30,-0.1,1.1), DrawFunc(f) );

Podrška za neizrazito upravljanje

Sustavi neizrazitog upravljanja definiraju se naredbom FuzzyControlSystem . Sintaksa je slijedeća:

FuzzyControlSystem naziv (
DefineVars( lista_ulaznih_varijabli ),
DefineVars( lista_izlaznih_varijabli ),
Rules(
Lista_pravila
),
identifikator_zaključivanja
);

Lista ulaznih varijabli i lista izlaznih varijabli je lista imena koja su odvojena zarezima i moraju biti međusobno različita. Lista pravila je lista poziva Rule funkcije koji su također odvojeni zarezima. Identifikator zaključivanja je broj koji određuje na koji se način izvodi zaključivanje o stvarnoj vrijednosti izalzne varijable, tj defazifikacija. Trenutno je podržan samo identifikator 1, koji određuje da se defazifikacija radi tako da se izvodi odsijecanje skupova iz TADA dijela pravila, radi se njihova unija (Zadehova), i zatim se računa CenterOfArea. Pravilo izvođenja pojedinih pravila je slijedeće: ukoliko se izvodi vrijednosti za izlaznu varijablu var1, tada se pale samo pravila koja definiraju tu varijablu. Sintaksa jednog pravila (Rule naredba) je slijedeća:

Rule(uvijet, naziv_izlazne_varijable, vrijednost_izlane_varijable )

Ukoliko je definiran neizraziti skup SKUP1 nad domenom M, i ukoliko je varijabla VAR definirana nad tom istom domenom, i ima neku zadanu vrijednost, tada se upit "koliko varijabla VAR pripada neizrazitom skupu SKUP" izvodi funkcijom ValueIn(SKUP,VAR). Na ovaj je način omogućena konstrukcija složenih upita u uvijetnom dijelu pravila. Npr.

FuzzyControlSystem sys1 ( DefineVars( brzina, smjer ), DefineVars( gas, okreni ), Rules( Rule( Min(ValueIn(brNULA,brzina),ValueIn(smjerKRIVI,smjer)), okreni, okretDA ), Rule( Max(Not(ValueIn(brNULA,brzina)),ValueIn(smjerPRAVI,smjer)), okreni, okretNE ), Rule( Not(ValueIn(smjerPRAVI,smjer)), gas, gasVELNEG ) ), 1 );

Ovo je isječak iz jednog sustava za upravljanje vozilom. Definiran je sustav neizrazitog upravljanja pod nazivom sys1. Definirane su ulazne varijable brzina i smjer, te izlazne varijable gas i okreni. Definirana su tri pravila.

1. AKO JE brzina = brNULA I smjer = smjerKRIVI TADA okreni = okretDA
2. AKO (nije (brzina = brNULA)) ILI smjer = smjerPRAVI TADA okreni = okretNE
3. AKO (nije (smjer = smjerPRAVI)) TADA gas = gasVELNEG

Na ovaj način može se definirati nekoliko sustava unutar jednog programa, jer se svi sustavi međusobno razlikuju po imenu. Međutim, unutar programa sustav se ne može "pokrenuti" direktno, već je razvijen mehanizam koji omogućava da se implementira posebna java klasa sa korisničke strane koja će zatim biti pokrenuta od strane FSIT-a i koja će moći komunicirati sa sustavima. Naime, svaka takva klasa mora implementirati slijedeće sučelje ExternalJavaCallClassI . Pri tome su još definirano druga sučelja poput FSITFuzzyControlSystemI i sl.

Ideja je slijedeća. FSIT podržava naredbu ExternalJavaCall koja ima sintaksu:

ExternalJavaCallnazivKlase;

Kada naiđe na tu naredbu, sustav će potražiti .class datoteku zadanog imena i učitati je. Ukoliko uspije, i ukoliko ta klasa implementira sučelje ExternalJavaCallClassI, tada će sustav pozvati člansku funkciju void Call(FSITI fsit) koja je implementirana u toj klasi. Program mora zapamtiti vrijednosti varijable fsit, i što prije vratiti kontrolu pozivatelju (ovo se može izvesti tako da se unutar tijela funkcija Call stvori nova nit koja će izvršavati zadatke te klase).

Program pojedinom sustavu za neizrazito upravljanje može pristupiti preko fsit.getFuzzyControlSystemByName("ime_sustava") . Ukoliko sustav nije definiran, rezultat će biti null. Inače će se dobiti referenca na sučelje FSITFuzzyControlSystemI.

Evo još u nekoliko rečenica odgovor na pitanje "Kako doći do rezultata"? Kada se dobije referenca na sučelje FSITFuzzyControlSystemI, potrebno je pozivima setVarValue postaviti vrijednosti u sve varijable koje su definirane kao ulazne za taj sustav (ukoliko se koriste za izvođenje pravila), te zatim pozvati funkciju getResultFor("naziv_izlazne_varijable") koja će uz prethodno postavljene ulazne vrijednosti izvesti vrijednost za traženu izlaznu varijablu. Ukoliko ima više izlaznih varijabli, biti će potrebno getResultFor pozvati onoliko puta koliko ima izlaznih varijabli.

Detaljniji opis postupka i prikaz svih sučelja može se pogledati na ovom linku .

Jedan kompletan primjer koji je uključen u FSIT program može se skinuti sa ovog linka .

RAD SA PERCEPTRONOM

Za simulaciju perceptrona koristi se Perceptron naredba (vidi detaljnije ). Lista podržanih perceptrona nalazi se na ovom linku . Jednostavni primjeri učenja perceptrona nalaze se na ovom linku .

RAD SA VIŠESLOJNIM PERCEPTRONOM

Za simulaciju ove mreže perceptrona koristi se MultiLayerPerceptron naredba (vidi detaljnije ).

Funkcije i sintaksa:
HamacherS(f1,f2,param)
HamacherT(f1,f2,param)
YagerS(f1,f2,param)
YagerT(f1,f2,param)
FrankS(f1,f2,param)
FrankT(f1,f2,param)
DuboisPradeS(f1,f2,param)
DuboisPradeT(f1,f2,param)
SugenoNot(f1)
YagerNot(f1)
ZadehS(f1,f2)
ZadehT(f1,f2)
ZadehNot(f1)
Max(f1,f2)
Min(f1,f2)
Not(f1)

FuzzyTrokut(a,b,c)
FuzzyTrapez(a,b,c,d)

Which(uvjet1,izraz1,uvjet2,izraz2,...) // opcionalno neki uvjet može biti ključna riječ default

Hamacher S i T, Yager S i T, Frank S i T te DuboisPrade S i T implementacije su istoimenih parametriziranih S i T normi. Ovo su binarne norme. Zadeh S i T implementacije su neparametriziranih Zadehovih S i T normi, te za njih vrijede identiteti koji su dani u nastavku. SugenoNot, YagerNot te ZadehNot implementacije su operacije negacije na način kako su to predložili Sugeno, Yager i Zadeh. Ovo su unarne operacije.

Funkcija Which omogućava da se definira funkcija po dijelovima. Uvjeti se evaluiraju redoslijedom kojim su navedeni, i prvi uvjet koji se izračuna kao istinit odrediti će vrijednost funkcije izrazom koji ga direktno slijedi. Umjesto uvjeta može se koristiti ključna riječ default što ima za posljedicu da se taj uvjet uvijek evaluira kao ispunjen.

Identiteti:
ZadehS == Min, ZadehT == Max, ZadehNot == Not == 1-x

Naredbe:
FuzzyFunc
SetParam
AnimateParam
SetRange
FrameRate
DrawFunc
FuzzyUniverse
SetAnimParamDecimals

Deklaracija nove funkcije:
FuzzyFunc FUNCNAME = funkcijski_izraz {@ [domain_definition | domain_name]};
{...} znači opcionalno, [a | b] znači obavezan izbor između "a" ili "b"

Postavljanje vrijednosti parametra "param":
SetParam(param,param_value);

Animacija parametra:
AnimateParam(param,min_value,max_value,number_of_steps);

Napomena: Samo unutar Drawing bloka!

Određivanje broja decimala animiranog parametra koji će se prikazivati:
SetAnimParamDecimals(number_of_decimals);
number_of_decimals mora biti nenegativan broj. Default vrijednost je 3.

Postavljanje koordinatnog sustava i granica iscrtavanja:
SetRange(x_min,x_max,y_min,y_max);

Napomena: Samo unutar Drawing bloka!

Postavljanje brzine animacije (broj sličica u sekundi):
FrameRate(x);

Napomena: Samo unutar Drawing bloka!

Iscrtavanje funkcije:
DrawFunc(func_name,{Color=color,PlotJoint=true});

Napomena: Samo unutar Drawing bloka!

Postavljanje naslova crteža:
SetTitle(naslov);

Napomena: Samo unutar Drawing bloka!

Boje:
white, red, green, blue, yellow, light_gray, dark_gray, gray, black, pink, orange, magenta, cyan

Aritmetički i logički operatori:

Konstante
PI .... pi, 3.14...
E .... e, 2.71...

Binarni operatori:
+ zbroj
- razlika
* umnozak
/ dijeljenje
^ potenciranje
Pow potenciranje
LogN logaritam po zadanoj bazi
ArcTanX računa kut na temelju koordinata točke

sintaksa je: NAZIV_OPERATORA ( ARG1, ARG2 )
npr.
+(f1,*(f2,f3))===>>> f1 + f2*f3
Pow(f1,3.) ===>>> f1 ^ 3
^(f1,3.) ===>>> f1 ^ 3
LogN(f1,3.) ===>>> logaritam od f1 po bazi 3.
ArcTanX(x,y) ===>>> izračun kuta na temelju x i y koordinate točke

Unarni operatori:
+ unarni plus
- unarni minus

sintaksa je: NAZIV_OPERATORA SLIJEDECI_IZRAZ
npr.
-f1
+f2
+(-f1,f2) ===>>> (-f1) + (f2)

Skraćeni unarni operatori:
Sqrt ... kvardatni korijen
Log .... logaritam po prirodnoj bazi (e)
Exp .... računa Pow(E,x)
Sin .... računa sinus kuta (kut u radijanima)
Cos .... računa kosinus kuta (kut u radijanima)
Tan .... računa tangens kuta (kut u radijanima)
ArcSin .... računa kuta iz sinusa (kut u radijanima)
ArcCos .... računa kuta iz kosinusa (kut u radijanima)
ArcTan .... računa kuta iz tangensa (kut u radijanima)
RadToDeg .... pretvorba kuta zadanog u radijanima u stupnjeve
DegToRad .... pretvorba kuta zadanog u stupnjevima u radijane

sintaksa je: NAZIV_OPERATORA(ARG)
npr.
Sqrt(f2)
Log(f1)

Ternarni:
Gauss(x,mi,sigma) ... mi=srednja vrijednost, sigma=standardna devijacija; standardna gaussova funkcija
GaussShaped(x,mi,sigma) ... mi=srednja vrijednost, sigma=standardna devijacija; gaussova funkcija bez skaliranja (max=1)

Logički operatori:
&& AND (binarni)
|| OR (binarni)
! NOT (unarni)

Operatori komparacije:
> veće
>= veće-jednako
< manje
<= manje-jednako
= jednako

sintaksa je: NAZIV_KOMPARATIVNOG_OPERATORA ( ARG1, ARG2 )
npr.
>=(f2,f3)===>>> f2 >= f3
&&(>=(f2,f1),<=(f2,f3)) ===>>> (f2 >= f1) AND (f2 <= f3)

Svi operatori izvedeni su kao funkcije, što znači da se npr.:
uvjet1 && uvjet2
piše kao:
&&(uvjet1,uvjet2)

Zadavanje domena:
FuzzyUniverse DOMAIN_NAME = domain_definiton;

Oblici domain_definition-a:
real enumerated {elem1,elem2,elem3,...,elemn};
real discrete {first_elem,last_elem,step};
real {lower_bound,upper_bound};
integer enumerated {elem1,elem2,elem3,...,elemn};
integer discrete {first_elem,last_elem,step};
integer {first_elem,last_elem,step};

Svi skupovi koji zadaju granice, umjesto neke od granica ili umjesto obje granice mogu koristiti ključnu riječ none kako bi odredili da nisu ograničeni sa tih strana. Npr.

integer discrete {-10,none,2};

određuje skup cijelih brojeva {-10,-8,-6,-4,-2,0,2,4,6,8,10,... +beskonačno}

Enumerirani skupovi omogućavaju zadavanje skupa navođenjem svih njegovih elemenata; npr. skup cijelih brojeva {1,3,8,15} može se zadati pomoću:
integer enumerated {1,3,8,15};

Uočite da je skup cijelih brojeva sam po sebi diskretan, pa integer i integer discrete imaju isto značenje!

Primjeri stvaranja domena:

FuzzyUniverse un1 = real enumerated {1.,2.,3.,4.,5.,6.,7.}; == {1,2,3,4,5,6,7}
FuzzyUniverse un2 = real discrete {0.,10.,2.}; == {0,2,4,6,8,10}
FuzzyUniverse un3 = real {1.,2.}; == [1,2]
FuzzyUniverse un4 = real discrete {1.,none,0.5}; == {1,1.5,2,2.5,3,3.5,... +beskonacno}

FuzzyUniverse un5 = integer enumerated {1,2,3,4,5,6,7}; == {1,2,3,4,5,6,7}
FuzzyUniverse un6 = integer discrete {0,10,2}; == {0,2,4,6,8,10}
FuzzyUniverse un7 = integer {1,4,1}; == {1,2,3,4}
FuzzyUniverse un8 = integer discrete {1,none,1}; == {1,2,3,4,5,6,... +beskonacno}

Autor programa je Marko Čupić, student na Fakultetu elektrotehnike i računarstva (FER). Sve eventualne pogreške u programu molimo javiti autoru na marcupic@netscape.net .