Na gornjem primjeru prikazan je preobražaj objekata u 2D prostoru. Uočljivo je kako početni i završni objekt imaju različite topologije. Početni objekt je kompaktan, dok je završni objekt isprekidan i rupičast. Prijelazi su vrlo prirodni i glatki.

Video sekvenca: cvijet_smajli.avi

U ovom primjeru izvršava se metamorfoza između objekata potpuno različitih struktura. Početni objekt ima oblik slova X, a završni oblik slova O. Klasičnim metodama bilo bi jako teško uspostaviti vezu između ova dva objekta, no ovdje se prijelazi dobivaju automatski, bez potrebe za posebnim definiranjem veza. Ako su objekti jako različiti, kao u ovom slučaju, dobiva se efekt kao da se prvi objekt polako topi, a onda se poneki preostali dijelovi spajaju u oblik drugog objekta.

Video sekvenca: x_o.avi

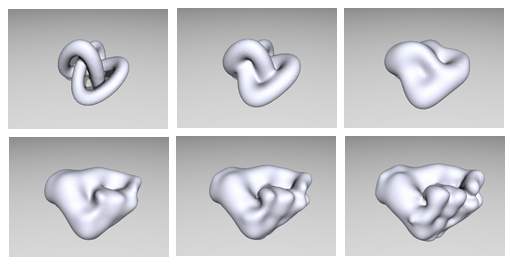
Iz primjera 3 se može vidjeti kako je metamorfoza u 3D prostoru, isto kao i u 2D prostoru, vrlo uspješna, čak i kod objekata različitih topologija. Za iscrtavanje objekata korišten je program POV-Ray.

Video sekvenca: knot_fist.avi

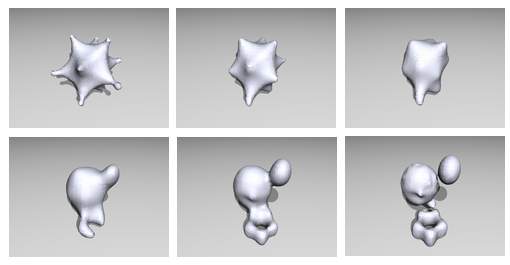
Primjer 4 je ekstreman primjer metamorfoze objekata s različitom topologijom. Krajnji objekt su zapravo tri potpuno nezavisna objekta ( dva kuglasta objekta i jedan torus ).

Video sekvenca: star_objects.avi

bunny_star.avi (potreban DivX 5.0 codec)
Za vizualizaciju je korišten POV-Ray.

cat_bunny.avi

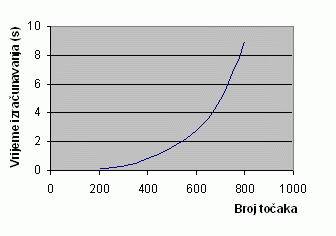
Dijagram 1 pokazuje prosječna vremena potrebna za rješavanje sustava, ovisno o broju definiranih točaka. Dijagram vrijedi i za 2D i za 3D prostor. Rješavanje sustava bit će otprilike jednako bez obzira na dimenziju jer se prelaskom u višu dimenziju dodaje zanemariv broj članova u sustav, te se ne povećava vrijeme izračunavanja. Iz dijagrama se može vidjeti kako povećavanjem broja točaka prilično naglo raste i vrijeme potrebno za rješavanje sustava. To je jedan od većih nedostataka ove metode. Sustav od 4000 točaka postaje praktički nerješiv, zbog dugotrajnosti izračunavanja

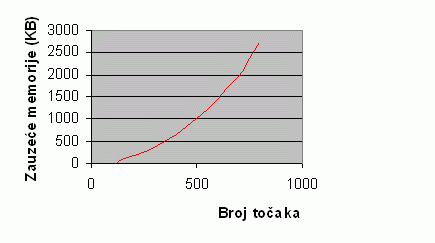
Najviše memorije troši se pri postavljanju matričnog sustava (3). Količina zauzete radne memorije raste kvadratno u odnosu na broj definiranih točaka i ovisi samo o broju točaka. Zapravo, postoji zanemarivo mala razlika u količini zauzete memorije između dva sustava s istim brojem točaka, ali koji se rješavaju u različitim dimenzijama. Npr. u 3D sustavu u matricu se dodaje i treća komponenta koordinate točke pa će ekvivalentno tome malo rasti i zauzeće memorije.

Uzmimo da se algoritam koristi za metamorfozu dva 3D objekta, s prosječnim brojem točaka 2500 (1250 rubnih točaka i 1250 točaka normale). Ukupan broj točaka će biti 5000. Matrica sustava će prema (3) imati (5000+1+4)^2 članova. Ako uzmemo da za zapis članova koristimo tip podatka float koji zauzima 4 byta, dobit ćemo ukupno zauzeće memorije od 100,200,100 bytova, odnosno otprilike 100 MB. U današnjim uvjetima ovakvo zauzeće memorije je prihvatljivo.