Nekoliko je jedinstvenih svojstava Yu-Kwokovog pristupa.
Permutacijom vrhova (u 2. koraku) i umetanjem
bitova vodenog iga u skupine tako permutiranih
vrhova (u 4. koraku) postignuto je da su podaci o
svakom pojedinom bitu distribuiran po različitim
dijelovima povrine objekta. Pored toga podaci o
vodenom igu u objekt se umeću promjenom duljine
niza vektora razapetih između pojedinih vrhova i
centra modela, a snaga s kojom se pojedini bit
umeće prilagođava se globalnim karakteristikama
modela, kao i lokalnim karakteristikama pojedinog
vrha. Na taj način ovako umetnuti vodeni ig
otporan je na moguće napade navedene u prvom
poglavlju.
To konkretno znači ovo: napadi poligonskom simplifikacijom,
zaglađivanjem objekta i premreavanjem mogu se
nakon postupka ponovnog uzorkovanja promatrati kao
podvrsta bijelog uma. Kako bi sustav bio to
otporniji na takvo unoenje uma, tijekom dohvata
vodenog iga koristi se vrijednost cijele skupine
razapetih vektora za dohvat jednog bita
informacije o vodenom igu. Napadi preslagivanjem
vrhova, nakon postupka ponovnog uzorkovanja nemaju
nikakav utjecaj na dohvat vodenog iga, dok za
obranu od napada lokalnim deformacijama i
operacijama odsijecanja sustav distribuira
informaciju o pojedinom bitu vodenog iga po
cijelom modelu. Napadi promjenom topologije modela
također nemaju nikakav utjecaj na dohvat naeg
vodenog iga budući da je vodeni ig skriven
unutar geometrijskih karakteristika objekta.
Kako bi se dodatno povećala robustnost ovakvog sustava za
umetanje vodenog iga parametri
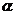 i M0ij u 4.
koraku kontroliraju snagu signala vodenog iga
koji se umeće. Takvim adaptivnim umetanjem vodenog
iga postignuto je da se vodeni ig u 3D objekt
moe umetnuti to neprimjetnije uz istovremeno
maksimalnu moguću snagu svakog pojedinog umetnutog
bita.
i M0ij u 4.
koraku kontroliraju snagu signala vodenog iga
koji se umeće. Takvim adaptivnim umetanjem vodenog
iga postignuto je da se vodeni ig u 3D objekt
moe umetnuti to neprimjetnije uz istovremeno
maksimalnu moguću snagu svakog pojedinog umetnutog
bita.
Postupak umetanja vodenog
iga odvija se na ovaj način:
1.
Zada se vodeni ig kao binarni niz
duine W=(w0, w1,...,wn-1);
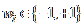 .
.
2.
Izmjeaj vrhove izvornog modela
prema zadanom koraku permutacije K:
V'=Permutiraj(V, K). Pri
tome Vo=(vo0,
vo1,...,voL-1)
predstavljaja vrhove izvornog modela, L
je broj vrhova modela a V'o =(v'o0,
v'o1,..., v'oL-1).
3.
Izaberi prvih S*N vrhova iz
skupa Vo' i podijeli ih u
N skupina V'oi=(v'oi0,
v'oi1, voi2,...,voS-1),
pri čemu je
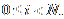 Svaka skupina sadri S
vrhova.
Svaka skupina sadri S
vrhova.
4.
Umetni po jedan bit vodenog iga u
svaku skupinu na ovaj način:
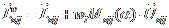 ,
,
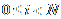 ,
,
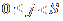 . Pri tome
. Pri tome
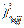 označava izvorni vektor
razapet između centra modela i j-tog
vrha i-te skupine,
označava izvorni vektor
razapet između centra modela i j-tog
vrha i-te skupine,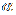 je parametar vodenog iga
koji određuje globalnu snagu umetnutog vodenog
iga, M0ij je parametar koji
određuje lokalnu snagu umetnutog iga i time
omogućuje da se snaga vodenog iga prilagođava
geometriji modela.
je parametar vodenog iga
koji određuje globalnu snagu umetnutog vodenog
iga, M0ij je parametar koji
određuje lokalnu snagu umetnutog iga i time
omogućuje da se snaga vodenog iga prilagođava
geometriji modela.
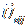 je jedinični vektor vektora
je jedinični vektor vektora
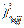 , dok je wi
i-ti bit vodenog iga.
, dok je wi
i-ti bit vodenog iga.
5.
Obnovi izvorni redoslijed vrhova
kakav je bio prije permutacije iz 2. koraka.
Postupak dohvata vodenog iga umetnutog na gore
opisani način prikazan je na odvija se na ovaj
način:
1.
Ako je 3D model koji se ispituje
translatiran, rotiran ili skaliran u odnosu na
na izvorni model, najprije je potrebno, takav
model dovesti na lokaciju i mjerilo u koje se
nalazi izvorni model. To se postie postupkom
registracije. Postoji nekoliko postupaka za
registraciju, od kojih su najpoznatiji oni
opisani u [Chen92] i [Besl92].
2.
U slučaju da je na modelu izvedena
neka od operacija koja mijenja topologiju mree,
kao to su poligonska simplifikacija,
odsijecanje, premreavanje i sl; nije moguće
izravno dohvatiti vodeni ig već je prethodno
potrebno iznova uzorkovati model.
3.
Kao i u koracima 2. i 3. postupka za
umetanje vodenog iga, i u postupku dohvata
vodenog iga potrebno je permutirati i
podijeliti u grupe vrhove izvornog modela kao i
modela iz kojeg se pokuava dohvatiti vodeni
ig. Tako se dobije N skupina vrhova V'oi=(v'oi0,
v'oi1, voi2,...,voiS-1)
izvornog modela i N skupina vrhova
Vdi'=(v'di1, vdi2,....,vdiS-1)
ispitivanog modela, pri čemu je
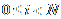 .
.
4.
Izračuna se razlika duljina između
vektora razapetih između pojedinih vrhova modela
i centra modela, pri čemu se za oba modela (i za
izvorni i za ispitivani) kao sredite modela
uzima sredite izvornog modela, to moemo
zapisati ovako: Doij=Ldoij
Looij pri čemu je
Looij duljina vektora
razapetog između centra izvornog modela i j-tog
vrha i-te skupine izvornog modela, dok je
Ldoij duljina
vektora razapetog između centra izvornog modela
i i j-tog vrha i-te skupine
ispitivanog modela.
5.
Svaka izračunata razlika duina
pomnoi se teinskim faktorom Woij
(o tome kako se taj faktor izračuna bit će
riječi u sljedećem poglavlju) te se izračunaju
sume razlika duina za svaku skupinu:
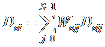
6.
Iz tako izračunatih suma skupina,
pročita se vodeni ig na način da je
|
wdi=sign(Doi),
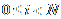 |
(4.1) |
7.
Izračuna se korelacija između
dohvaćenog vodenog iga i umetnutog vodenog iga
kako bi se procijenilo da li je traeni vodeni
ig prisutan u ispitivanom modelu. Koristi se
linearna korelacija između ta dva vodena iga:
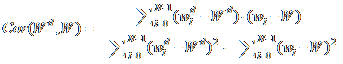 |
(4.2) |
Wd označava dohvaćeni vodeni ig, W
je umetnuti vodeni ig,
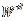 je srednja vrijednost od Wd,
je srednja vrijednost od Wd,
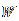 je srednja vrijednost od W,
a N je duina vodenog iga (odnosno broj bitova
iga). Ako izračunata korelacija prelazi
određeni prag ThrD, zaključujemo da
je vodeni ig prisutan u ispitivanom modelu.
je srednja vrijednost od W,
a N je duina vodenog iga (odnosno broj bitova
iga). Ako izračunata korelacija prelazi
određeni prag ThrD, zaključujemo da
je vodeni ig prisutan u ispitivanom modelu.