U ovom poglavlju bit će predstavljeni osnovni
algoritmi za vodene igove primjenjivi na 3D
objektima. Opisane algoritme predloili su 1997.
znanstvenici Ryutarou Ohbuchi, Hiroshi Masuda i
Masaki Aono iz IBMovog istraivačkog
laboratorija u Tokyu [Ohbuchi97]. Predloene
tehnike mogu se grubo podijeliti u dvije
skupine. Prvu skupinu čine metode koje djeluju
na geometriju mree trokuta, dok drugu skupinu
čini algoritam koji djeluje na topologiju mree
trokuta.
Metode koje djeluju na geometriju mree
poligona, naročito predloeni TVR (Tetrahedral
Volume Ratio) algoritam, ima gotovo
optimalna svojstva u pogledu kapaciteta i
brzine. Nedostaci su mu ranjivost na operacije
premreavanja i poligonsku simplifikaciju.
Metoda koje mijenjaju topologiju, u osnovi umeće
informaciju stvaranjem upljina u izvornoj
mrei.
Postoje dvije vrste atributa u poligonalnim mreama koje se
mogu mijenjati da bi se umetnuo vodeni ig. Prva
je geometrija i geometrijski primitivi
(npr. točke ili trokuti), dok je druga
topologija između tih primitiva.
Jedinice koje se mijenjaju (bilo geometrijske,
bilo topoloke) obično se nazivaju primitivima
umetanja (embedding primitives).
·
Geometrijski primitivi
umetanja
Geometrijske vrijednosti,
naročito koordinate vrhova, mogu se mijenjati
kako bi se u objekt umetnuo vodeni ig. Međutim,
takva informacija koja se umeće izravno u
promjenu poloaja koordinate je osjetljiva na
gotovo svaku geometrijsku transformaciju. Iz tog
je razloga bolje koristiti primitive koji su
invarijantni na određene skupine geometrijskih
transformacija. U nastavku je dan pregled
primitiva umetanja koji su invarijantni na
određenu skupinu geometrijskih transformacija:
1.
Primitivi
osjetljivi
na sve dole navedene transformacije :
a. Koordinata točke.
2. Primitivi invarijantni na
translaciju i rotaciju :
a. Duljina linije.
b. Povrina poligona.
c Volumen poliedra.
3. Primitivi invarijantni na
translaciju, rotaciju i uniformno skaliranje:
a. Dvije veličine koje definiraju skup
sličnih trokuta (npr. dva kuta).
b. Omjer povrina dva poligona.
4. Primitivi invarijantni na afine
transformacije
a. Omjer duljina dva
paralelna segmenta linije
b. Omjer volumena dva poliedra.
·
Topoloki primitivi umetanja
Vodeni ig moe biti umetnut u 3D objekt također i
promjenom na topologiji modela. Ovakva promjena
moe imati kao posljedicu i promjene u geometriji
(npr. promjenu poloaja vrhova), ali informacija
je umetnuta prvenstveno djelovanjem na topologiju.
U
praktičnoj primjeni za umetanje podatka u 3D
objekt potrebno je napraviti izmjene na velikom
broju primitiva umetanja kako bi se mogla
pohraniti dovoljna količina podataka za vodeni
ig.
Kao to je već u uvodu napomenuto problem kod 3D
objekata je taj da ne postoji nikakav implicitni
poredak tih primitiva, pa ih je prethodno potrebno
na neki način poredati. Za poligonalne 3D objekte
to je moguće učiniti na slijedeća dva načina:
1. Topoloko uređenje
Ovakvo uređenje zasniva se na svojstvu susjedstva,
kao to je susjedstvo vrhova, kako bi se poredali
primitivi umetanja. Topoloko uređenje primjenjivo
je i na topoloke i na geometrijske primitive
umetanja i otporno je na promjene izazvane
geometrijskim transformacijama ali naravno ne i na
one izazvane topolokim modifikacijama.
2. Kvantitativno uređenje
Ovakvo uređenje zasniva se na nejednakostima među
određenim veličinama primitiva umetanja (npr.
nejednakostima između volumena različitih
poliedara) kako bi se izvelo sortiranje tih
primitiva.
U
obje navedene metode često je neophodno zadati
početni uvjet (npr. prvi primitiv) kako bi se
omogućilo sortiranje. Naravno i sortiranje i
početni uvjet morali bi biti robustni na moguće
promjene poput geometrijskih transformacija, ili
će vodeni ig biti izgubljen.
Vrste uređenja primitiva moguće je podijeliti po
opsegu djelovanja na lokalna, globalna, i uređenje
po indeksu. Na slici 2-1 ilustrirane su sve tri
vrst sortiranja.
1.
Globalno uređenje
Kod ovakvog uređenja svi primitivi unutar objekta
u koji se eli umetnuti vodeni ig promatraju se
kao jedan skup.
2. Lokalno uređenje
Kod lokalnog uređenja primitivi se dijele u
nekoliko skupova i primitivi se sortiraju za svaki
skup pojedinačno
3. Uređenje po indeksu
Ovo uređenje vrlo je slično lokalnom uređenju, ali
se promatra vrlo mali podskup (dakle podskup od
svega nekoliko primitiva) koji se naziva MEP
(Macro-Embedding-Primitive).
Svakom MEPu pridruen je jedinstveni indeks koji
određuje redoslijed primitiva.

Slika 2-1.
Primjeri za (a) globalno, (b) lokalno i (c)
uređenje po indeksu [Ohbuchi97].
Globalno uređenje obično daje veći kapacitet
zapisa, međutim lokalno i uređenje po indeksu
omogućuju da se u isti poruka zapie u objekt
viestruko (u svaki podskup odnosno u svaki MEP)
čime je osigurana veća otpornost kod, primjerice,
odsijecanja dijela modela.
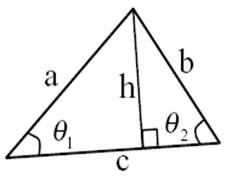
TSQ algoritam kao primitiv umetanja koristi dvije
veličine koje definiraju skup sličnih trokuta kako
bi umetnuo vodeni ig u 3D objekt predstavljen
mreom trokuta. Na slici 2-2 prikazan je jedan
takav par sličnih trokuta koji mogu biti određeni
skupom {b/a, h/c} ili skupom {Θ1,
Θ2}.
Kako bi odredio poredak primitiva, algoritam
koristi četvorke koje se sastoje od 4 susjedna
trokuta koji tvore konfiguraciju prikazanu na
slici 2-3. Svaka takva četvorka predstavlja jedan
MEP. U svakom MEPu pohranjene su četiri podatka {Marker,
Indeks, Podatak1, Podatak2}. Marker (M)
je par gore navedenih vrijednosti koji definira
MEP. Indeks (S) sadri redni broj MEPa, Podatak1 i
Podatak2 (D1 i D2) sadre podatke koji se umeću.
 |
 |
|
Slika 2-2. Primjer para veličina koji definira
skup sličnih trokuta. |
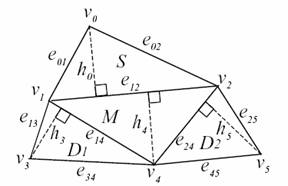
Slika 2-3 Primjer jednog MEPa. Vi
označava vrh, eij je duljina brida,
a hi je visina trokuta.
|
Svaki MEP je prema tome određen topologijom, dok
se MEPovi uređeni kvantitativno, prema rednom
broju indeksa.
TSQ algoritam ne
zahtijeva originalni 3D model za detekciju
vodenog iga, međutim zahtijeva par vrijednosti
koji definiraju trokute-markere. Vodeni ig
umetnut ovim postupkom otporan je odsijecanje
dijela objekta i na lokalne deformacije, budući
da je upotrijebljeno uređenje po indeksu pa se
vodeni ig redundantno umeće u 3D objekt. Vodeni
ig moe biti uniten globalnim deformacijama na
cijelom objektu ili opsenom izmjenom topologije
(primjerice premreavanjem).
TSQ algoritam umetanja vodenog iga odvija se u
ovim koracima:
(1) Obilazi se
ulazna mrea trokuta u potrazi za četvorkama
trokuta koje će biti upotrijebljene kao MEPovi.
Pri tome treba izbjegavati vrhove koji su već
upotrijebljeni za umetanje podataka ili koji su
zbog premalih dimenzija neprikladni za pohranu
podataka.
(2) Postavi vrijednost markera u centralni
trokut MEPa mijenjanjem njegovog skupa koji
definira slične trokute
{e14/e24,
h4/e12},
a to se postie promjenom koordinata vrhova v1,v2
i v4 za malne iznose (slika 2-3).
(3) Umetni
indeks i dva podatka u preostala tri trokuta
MEPa promjenom koordinata vrhova v0,
v3 i v5 koji nisu
zajednički s trokutom markerom. Indeks se umeće
u par {e02/e01, h0/e12},
a dva podatka umeću se parove {e13/e34,h3/e14}
i {e45/e25, h5/e24}.
Za svaki od ta tri trokuta algoritam prvo
mijenja omjer hi/eij tako
da prvo promijeni hi, a onda mijenja
eij/ekl zadravajući hi
konstantnim.
(4) Ponovi
korake (1) do (3) sve dok se ne umetnu svi
podaci.

Slika 2-4.
Vide se pojedinačni MEPovi. Svaki MEP sastoji se
od 4 trokuta u opisanoj konfiguraciji [Ohbuchi97].
U koracima (2) i
(3) promjene koordinata moraju biti izabrane tako
da omoguće zapis to veće količine podataka, a
takva promjena mora u isto vrijeme biti dovoljno
velika da bude otporna na unos uma u model i
dovoljno mala da ne narui vizualni izgled modela.
Uz zadanu mreu s umetnutim vodenim igom TSQ
algoritmom i uz zadani par vrijednosti koji
definiraju trokute-markere, postupak dohvata
vodenog iga odvija se u sljedećim koracima:
(1) Obilazi se uzlazna mrea trokuta u
potrazi za trokutom koji je označen markerom, čime
se locira MEP. Budući da je moguće da je objekt
mijenjan rezultat je probabilistički, odnosno u
nekim slučajevima moguća je pogreka.
(2) Pročitaj indeks i dva podatkovna
simbola iz odgovarajućih trokuta u MEPu.
(3) Ponovi korake (1) i (2) za sve trokute
markere u zadanoj mrei.
(4) Poredaj sve dohvaćene simbole prema
njihovim indeksima.
Jednostavan
postupak za oporavak od pogrene detekcije kod TSQ
algoritma sastoji se u tome da se ista poruka
zapie u objekt nekoliko puta, te se pri dohvatu
poruke zapisani simbol određuje po pravilu većine.
Vrijeme izvođenja
algoritma je otprilike proporcionalno broju
trokuta.
Primitiv umetanja kod TVR algoritma opisanog u
ovom dijelu je omjer volumena dva tetraedra.
Primitivi umetanja topoloki mogu biti uređeni
globalno ili lokalno. Algoritam ne zahtijeva
izvorni 3D model da bi dohvatio vodeni iga iz
objekta. Vodeni ig umetnut TVR algoritmom otporan
je na afine transformacije na objektu, ali će biti
uniten topolokim modifikacijama kao to su
premreavanje.
Jedna modifikacija TVR algoritma opisana na kraju
odjeljka je otporna i na odsijecanja i lokalne
transformacije, to je postignuto lokalnim
uređenjem primitiva umetanja i viestrukim
umetanjem iste poruke.
Osnovni problem kod nemodificiranog TVR algoritma je
pronalaenje globalnog jednodimenzijskog poretka
primitiva izmjene. Algoritam se odvija u sljedećim
koracima:
(1) Pronađi na ulaznoj mrei M razapinjuće stablo
vrhova Vt (engl. vertex tree),
uz zadane početne uvijete Ivt za
stablo Vt. Pretvori Vt
u niz trokuta Tris (triangle
sequence).
(2) Pretvori Tris u niz tetraedara Tets
(engl. tetrahedron sequence). Da
bi to učinili izračuna se zajednički vrh tetraedra
kao centroid koordinata prvih nekoliko trokuta
(primjerice prva tri). Upotrijebljeni trokuti
uklanjaju se iz niza, tako da njihove koordinate
ostaju nepromijenjene nakon umetanja vodenog iga.
(3) Pretvori Tets u niz omjera volumena Vrs
(engl. volume ratios sequence).
Da bi to učinili volumen jednog tetraedra iz niza
Tets (primjerice prvog)
izabere se kao zajednički nazivnik svih omjera, a
volumeni preostalih tetraedara upotrijebe se kao
brojnici.
(4) Umetni simbol u svaki omjer na način da se promijene koordinate
tetraedara iz brojnika. Promjena koordinata pri
umetanju tekućeg simbola ne smije interferirati s
promjenama nastalim prijanjim umetanjima
|

Slika 2-5. Trokuti
upotrijebljeni u TVR algoritmu su
potamnjeni. |
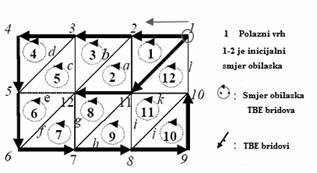
Slika 2-6. Prikazan je
primjer razapinjućeg stabla vrhova,
prikazani su elementi TBE liste, kao i
redoslijed dodavanja trokuta u Tris listu. |
Da bi generirali
stablo vrhova Vt obilazi se stablo uz
zadane početne uvijete Ivt zadane u obliku
para vrijednosti {početni vrh, početni smjer
obilaska}. U svakom vrhu, obilaskom
bridova u smjeru suprotnom od kazaljke na satu,
pronalazi se brid koji već nije u uvrten u Vt
i koji ne povezuje vrh s nekim vrhom koji je već
pokriven nekim drugim bridom iz Vt. Ako je
takav brid pronađen uvrsti se u Vt.
Na primjeru sa slike 2-6 razapinjuće stablo vrhova
ima korijen (i točku grananja) u vrhu označenom
brojem 1. Nakon prolaska kroz vrhove 1 do 10,
obilazak započinje ponovno iz vrha 1 i dodaju se
vrhovi 11 i 12.
Razapinjuće stablo Vt pretvara se u niz
trokuta formiranjem skupa bridova TBE
(Triangle Bounding Edge). Tbe je
inicijalno popunjen svim bridovima iz stabla
bridova Vt. Skup Tbe se popunjava na način
da se po razapinjućem stablu obilaze svi vrhovi,
te se u svakom vrhu u smjeru kazaljke na satu
trae svi susjedni bridovi. Svaki takav susjedan
brid dodaje se u skup Tbe, ako već nije u njemu.
Niz trokuta Tris je inicijalno prazan a
popunjava se sa odgovarajućim trokutom čim se sva
tri brida trokuta pojave u skupu Tbe.
U primjeru 2-6 bridovi (osim onih inicijalno
dodanih u skup Tbe, koji čine razapinjuće stablo)
označeni su abecedno prema redoslijedu uvrtavanja
u skup Tbe. Na istoj slici brojevima u kruićima
su označeni i trokuti prema redoslijedu dodavanja
u skup Tris.
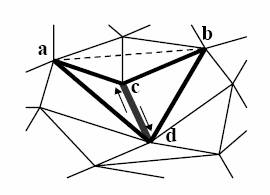
Slika 2-7.
Primjer računanja volumena a-b-c-d za brid c-d.
Slika pokazuje i dva moguća početna smjera
kretanja po bridu c-d.
TVR algoritam
umjesto početnog uvjeta zadanog u obliku {početni
vrh, početni smjer obilaska} prihvaća
početni uvjet zadan u obliku inicijalnog brida.
Kako bi izabrao inicijalni brid, algoritam
izračunava za svaki brid u modelu volumen
tetraedra formiranog od dva susjedna trokuta koji
dijele zadani brid (slika 2-7). Kao inicijalni
brid izabire se onaj kojem je volumen pripadajućeg
tetraedra najveći.
Ovaj postupak je
efikasan zato jer afine transformacije ne
naruavaju nejednakosti među volumenima tetraedara
(iako je potrebno naglasiti da je ovaj skup
tetraedara drugačiji od skupa tetraedara
upotrijebljenih za pohranu simbola u sam objekt).
Pri dohvatu
umetnutih simbola, ispravan početni brid se
pronalazi metodom pokuaja i pogreaka. Algoritam
isprobava vie potencijalnih početnih bridova dok
ne pronađe ispravan, unaprijed određen, početni
niz (lead-in symbol sequence). Ovo je
potrebno jer je moguće da zbog uma umetnutog u
objekt, brid sa s najvećim volumenom pripadnog
tetraedra ne bude ispravan početni brid.
Upotreba brida kao
početnog uvjeta ostavlja dva jednakovrijedna
moguća početna smjera za obilazak mree. Ova
dvoznačnost također se razrjeava metodom pokuaja
i pogreaka.
TVR algoritam dohvaća početni niz koristeći obje
mogućnosti, te izabire onaj smjer kojim se
ispravno dohvaća početni niz.
Vrijeme izvođenja
TVR algoritma je, slično kao i kod TSQ algoritma i
otprilike proporcionalno broju bridova.
Kao to je u uvodu
spomenuto vodeni igovi umetnuti TVR mogu se
učiniti, do određene mjere, otpornim na
odsijecanja i lokalne deformacije upotrebom
lokalnog uređenja primitiva (ili uređenja po
indeksu) te viestrukim umetanjem istog vodenog
iga u tako priređen model. Ova inačica algoritma
naziva se TVRC (engl. TVR Cluster) Kako bi
se stvorile odgovarajuće poddomene za lokalno
uređenje, algoritam jednostavno podijeli model na
nekoliko podskupova, odnosno na nekoliko
nepovezanih mrea trokuta. Granice takvih mrea
moraju imati zajedničke vrhove i bridove kako se
ne bi mogla uočiti mjesta diskontinuiteta.
|
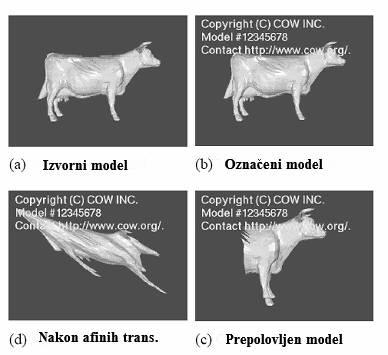
Na slici 2-8. prikazan
je model krave obiljeen ovako modificiranim
algoritmom. Poruka umetnuta u model ostala
je čitljiva nakon primjene vie uzastopnih
afinih transformacija, kao i u nekim
slučajevima u kojima je dio modela bio
odrezan.
|
TSPS algoritam odvaja (ljuti) određene zone iz ulazne
mree trokuta kako bi u model umetnuo vodeni
ig. Primitiv umetanja je susjedstvo para
trokuta u ulaznoj mrei, pri čemu svaki primitiv
kodira jedan bit vodenog iga (ulaznog niza
simbola). Na ovaj način definiran primitiv
implicitno određuje i njihov poredak. Budući da
TSPS algoritam radi s topolokim primitivom
umetanja, ovako umetnuti vodeni ig praktično je
otporan na bilo kakve geometrijske
transformacije. Viestrukim umetanjem istog
vodenog iga moe se učiniti otpornim i na
odsijecanja dijela modela. Pri dohvatu vodenog
iga iz markiranog modela, nije potreban
nemarkirani original.
Nedostatak ovog algoritma je relativno slaba iskoristivost
ulaznog modela.
Umetanje vodenog iga u model kod TSPS algoritma odvija se u
ovim koracima:
(1)
Odaberi u ulaznoj mrei M jedan
brid e i počevi od njega izradi zonu
trokuta S na ulaznoj mrei, koristeći
bitove iz ulazne poruke kako bi se odredila
spojnost među trokutima u toj zoni.
Kao to se na slici 2-9 vidi na ovaj način
građena zona trokuta ima na krajevima dva
slobodna brida koji se mogu poredati na način da
jedan označava 0 a drugi 1. To se moe
postići na način da se bridovi uvijek obilaze
ili u smjeru suprotnom kazaljci na satu ili u
smjeru kazaljke na satu, pri čemu prvi slobodan
brid na koji naiđemo označavamo s 0, a drugi s
1. Nakon to smo na ovaj način odredili
značenje pojedinog slobodnog brida moemo
odabrati slobodan brid na koji ćemo nadovezati
sljedeći trokut iz zone, zavisno o tome treba li
kodirati nulu ili jedinicu u ulaznom nizu
bitova.
(2)
Odvoji od ulazne mree M tako
stvorenu zonu S na način da se odcijepe
svi bridovi od M koji graniče sa S,
osim početnog brida e. Na ovaj način zona
S ostala je povezana s početnom mreom
M jedino zajedničkim početnim bridom. Kako
odvojena (oljutena) zona trokuta
prekriva cijelu rupu nastalu na ovaj način,
vodeni ig umetnut ovim algoritmom nije vizualno
uočljiv.
Mrea s umetnutim vodenim igom naziva se M+
mrea, a mrea M+
bez zone trokuta S naziva se
ablonska mrea (engl. stencil mesh)
R. Brid e slui kao početni uvjet za
dohvat vodenog iga, tj. zone trokuta S
(slika 2-12).

Slika 2-9. TSPS algoritam zapisuje vodeni ig u
spojnost zone trokuta S. Nakon takvog umetanja
zona S se odspaja od mree M a zadrava se samo
inicijalni brid e.
Na slici 2-10 prikazan je primjer zone trokuta koja počinje
bridom e i koja je nastala umetanjem ulaznog
niza bitova 10101101011 u slijed od 12
trokuta. Svaki bit ulaznog niza određuje u kojem
će se smjeru iriti mrea. Na taj način poruka,
koja bi se trebala umetnuti, mogla bi sgenrirati
zonu trokuta koja ne stane u ulazni model.
Primjerice za ulazni niz koji sadri veliki broj uzastopnih
nula ili jedinica zona trokuta bi se irila samo
u jednom smjeru i moglo bi se desiti da takva
mrea dođe do granica ulaznog modela (ili da se
kruno vrati na početak) prije nego li je
postala dovoljno velika da se umetnu svi
elementi ulaznog niza bitova. Da bi rijeili
ovaj problem oblik zone trokuta S moramo
prilagoditi ulaznom modelu dodavanjem posebnih
bitova, a i mjesto i smjer zone S treba biti
paljivo izabrano u modelu M. Posebno dodani
bitovi kojima prilagođavamo oblik zone S,
nazivaju se pokaznim simbolima (engl.
steering symbols). Pokazni simbol je bit
koji ne nosi nikakvu informaciju nego je umetnut
isključivo radi prilagodbe zone S proizvoljnom
obliku ulazne mree M.

Slika 2-10
Spojnost zone od 12 trokuta upotrijebljena je za
kodiranje niza od 11 bitova 101011010101.
Ti pokazni simboli isprepleteni su podatkovnim simbolima
(odnosno onima koji nose korisni sadraj u
vodenom igu). Nedostatak ovog pristupa je taj
to koritenje pokaznih simbola smanjuje
efektivni kapacitet ulaznog modela. Za izbor
najboljeg mjesta za umetanje zone trokuta S,
algoritam predviđa jednostavnu upotrebu
metode pokuaja i pogreaka.
Dohvat umetnute poruke izvodi se u ovim koracima:
(1)
Obilazi ulaznu mreu M+
dok ne pronađe brid s topolokim svojstvima koja
odgovaraju bridu koji započinje zonu trokuta,
poznate duljine, spojenu za ablonsku mreu
zajedničkim rubom.
(2) Obiđi zonu trokuta dok ne dođe do slobodnog kraja.
Slika 2-11 prikazuje primjer djelovanja TSPS algoritma na
mrei od 214 s koje je skinuta zona od 27 trokuta.
Od tih 27 trokuta 13 granica nosi podatkovne
bitove, a 13 pokazne bitove.
 |
 |
|
Slika 2-11 Zona trokuta koja se sastoji od 27
trokuta unutar mree od 215 trokuta. 13 bitova
je podatkovnih, 13 pokaznih. |
Slika 2-12 Mree M, M+,
R i zona trokuta S.
|
|