Redukcijski algoritmi
Redukcijski algoritmi rubova se koriste za rješavanje kartogramskih problema u raznim ponuđenim algoritmima. Očuvanje globalnog oblika je vrlo važno pri stvaranju prepoznatljivih kartograma. Korišteni redukcijski algoritam uzima to u obzir tako da pojednostavljuje globalne i unutarnje poligone na isti način.
Redukcija globalnog poligona
Ključno zapažanje je da važnosti vrhova poligona variraju u velikim omjerima. Vrhovi s kutovima blizu 180 stupnjeva i oni s kratkim rubovima nisu toliko značajni za oblik poligona dok oni s oštrim kutovima ili dugim rubovima imaju značajan učinak. Osnovna ideja algoritma redukcije globalnog poligona je da se ocijene važnosti svakog vrha prema tom kriteriju. Tada se iterativno manje važni vrhovi uklanjaju. Uklanjaju se samo oni vrhovi koji ne pripadaju većem broju poligona kako bi se održala topologija. Kako bi ostvarili algoritam redukcije prvo se definira notacija važnosti vrha na slijedeći način:
 , |
(1) |
gdje su 
i 
dva ruba vrha 
, a 
je funkcija koja vraća vrijednost važnosti kuta 
vrha 
. Funkcija važnosti 
je bitna jer različiti kutovi imaju drugačiji utjecaj na oblik poligona. Oštri kutovi i kutovi koji su blizu 90° su važniji za oblik poligona i funkcija važnosti zato dodjeljuje veće vrijednosti oštrim kutovima i manje vrijednosti tupim kutovima. U ovom algoritmu se koristi slijedeća funkcija:
 |
(2) |
Ona ima šiljke za 
i blizu je nule za 
. Domena funkcije je 
, a 
je odabran da bude 
. Slika 1 prikazuje težinsku funkciju važnosti kuta.
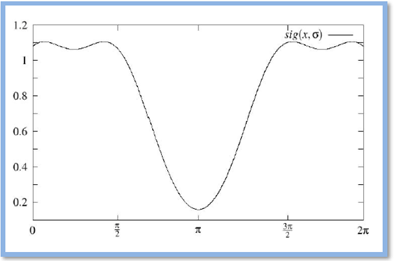
Slika 1: Težinska funkcija važnosti kuta.
Za ostvarenje algoritama redukcije vrhova globalnog poligona mora se definirati globalni poligon kao podskup vrhova iz P (skup ulaznih poligona koji označavaju regije karte). Za svaki poligon 
, dijelove globalnog poligona GP se može definirati kao:
 |
(3) |
Globalni poligon se definira kao 
. Algoritam za redukciju vrhova globalnog poligona je prikazan algoritmom 1. Može se vidjeti da se kao kandidati za uklanjanje razmatraju samo oni vrhovi koji ne pripadaju većem broju poligona (pogledati inicijalizaciju 
u algoritmu 1.) i uklanjaju se samo ako je izazvana razlika površina manja od zadane vrijednosti 
.
Algoritam 1: Algoritam redukcije vrhova globalnog poligona.
Redukcija vrhova unutarnjih poligona
Za redukciju unutarnjih vrhova može se ponovo koristiti algoritam korišten pri uklanjanju vrhova globalnog poligona uz drugačiju inicijalizaciju skupine vrhova
koje razmatramo za uklanjanje. Vrhovi koji pripadaju toj skupini su svi unutarnji vrhovi koji nisu spajajući odnosno oni koji pripadaju samo dvama poligonima.
Na slici 2 se vidi karta prije i nakon redukcije globalnih i unutarnjih vrhova.
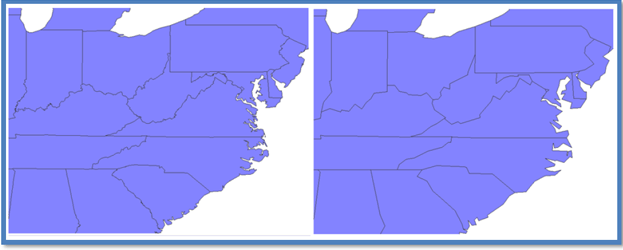
Slika 2: Primjer redukcijskog algoritma.