Osnova
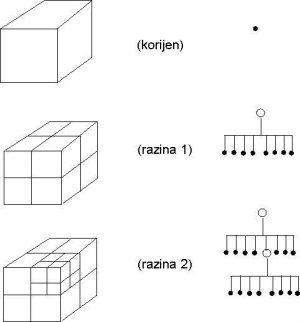
Oktalno stablo (engl. octree) je, kako i samo ime nalaže, stablasta struktura podataka. Svaki čvor se širi na osam elemenata koji mogu biti listovi ili daljnji čvorovi. Fizikalna aproksimacija oktalnog stabla je kocka koja obuhvaća cijeli prostor (zatvoreni sustav). Ta kocka predstavlja korijen stabla. Sljedeću razinu dobivamo podjelom kocke na osam jednakih dijelova kako je prikazano na slici. Svaka od novonastalih kocaka je korijen sljedeće razine ukoliko nastavimo s podjelom. U suprotnom predstavlja list trenutne razine.
Osnovna svrha oktalnog stabla je podjela prostora. Prostor se usitnjava podjelom stabla po razinama. Svaka razina označava veću podjelu i manju jedinicu prostora. Samim tim usitnjavanjem se smanjuje broj elemenata po jedinici prostora. Svaka kocka, bilo čvor ili list stabla, grupira susjedne elemente na tom dijelu prostora. Samim tim se smanjuje broj računanja međudjelovanja između pojedinih elemenata. Kao primjer toga se može uzeti kolizija.
Primjena kod kolizije
Osnovni i najjednostavniji algoritam računanja kolizije je uspoređivanje svakog elementa sa svakim. Kod malog broja elemenata algoritam daje dobre rezultate no kako složenost ovog algoritma raste eksponencijalno možemo zaključiti da kod praktičnih problema gdje broj elemenata iznosi nekoliko milijuna jedinki algoritam više nije ekonomičan.
Oktalna struktura nam ovdje pomaže. Kako smo već rekli osnovna zadaća oktalne strukture je podjela prostora na manje cjeline i grupiranje susjednih elemenata. Nemamo više potrebu za uspoređivanje svakog elementa sa svakim jer već na početku znamo da određeni elementi nisu dovoljno blizu jedan drugome da bi njihovo međudjelovanje bilo moguće.
U nekom idealnom slučaju podjele stablaste strukture dobili bismo potpuno izgrađeno stablo. To znači da bi cijeli prostor bio jednoliko usitnjen. U stvarnim situacijama nam to nije potrebno. Ne možemo očekivati da će elementi biti jednoliko raspršeni po prostoru. Na nekim mjestima će ih biti više dok ih na nekim neće biti uopće. Upravo zbog toga neke dijelove prostora, odnosno neke grane stabla ne trebamo dalje dijeliti dok nam je kod drugih podjela još uvijek potrebna. Ako imamo velik dio praznog prostora ili mali broj elemenata na nekom većem prostoru dovoljna nam je i jedna velika kocka koja će sve to obuhvatiti. Suprotno od toga ako je velik dio elemenata grupiran na malom prostoru taj će prostor zahtijevati veću odnosno sitniju podjelu.
Dodatni način raspodjele oktalnog stabla
Nakon što je podjela obavljena jedini elementi stabla koji nas konkretno zanimaju su listovi stabla. Čvorovi stabla nam služe samo pri pretrazi pojedinih elemenata i pri uvidu u odnose između kocaka. U pojedinim slučajevima moramo preciznije definirati podjelu prostora. Već smo rekli da jednaka razina podjele na cijelom prostoru nije dobra. U nekim slučajevima nam ni potpuno nepravilna podjela ne pomaže u dobivanju željenih rezultata. Ono što nam je potrebno je do određene razine polupravilna raspodjela prostora, tj. dodajemo određene uvjete pri čemu specificiramo da, npr, razlika razina raspodjele između dvije susjedne kocke ne smije biti veća od jedan.
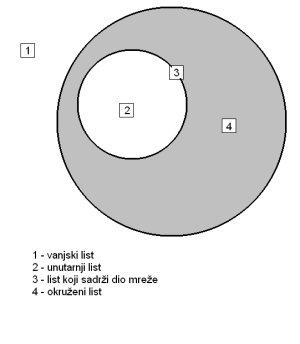
Ukoliko dijelimo prostor s nekom mrežom u sebi može se javiti potreba klasifikacije listova stabla. Kako smo rekli listovi stabla unutar sebe mogu, ali i ne moraju sadržavati elemente (u ovom slučaju dijelove mreže). S listovima koji sadrže nešto unutar sebe je sve jasno, ali ne i s onima koji obuhvaćaju prazan prostor. Njih možemo klasificirati u tri dodatne skupine: vanjski, unutarnji i okruženi. Vanjski je onaj koji se nalazi izvan mreže, unutarnji onaj koji se nalazi unutar mreže, a okruženi je onaj koji se nalazi izvan mreže, ali je njom okružen što je prikazano na slici.