Metode zasnovane na Lagrangeovim mrežama

Integracija po vremenu deformabilnih elemenata računski je zahtjevna operacija na objektima koji ima beskonačno mnogo točaka. Uvođenjem diskretizacije i primjenom numeričkih metoda mogu se dobiti vrlo dobre aproksimacije koje ne zahtijevaju toliko resursa.

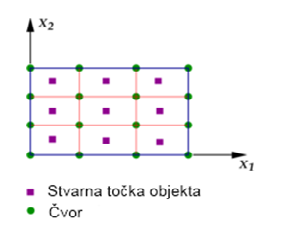
Lagrangeova mreža je zapravo rezultat metode diskretizacije tijela (engl. meshing). Metoda objekt podjeli u konačno mnogo elemenata, koji su obično predstavljeni nekim jednostavnim geometrijskim oblikom ili tijelom. Ti elementi se sastoje od čvorova i atributa. Čvorovi označavaju posebne točke elementa nad kojima se vrše vanjski utjecaji na objekt ili u kojima su elementi spojeni sa čvorovima drugih objekata. Atributi su zapravo svojstva materijala i stvarnih točaka koje opisuju objekt.

Slika 1. Primjer dvodimenzionalne Lagrangeova mreže



Metoda konačnih elemenata

Metoda konačnih elemenata je numerička metoda za rješavanje rubnih vrijednosti koja se temelji na fizičkoj diskretizaciji. Razmatrano područje dijeli se na konačni broj manjih područja, podskupova početnog područja, te ih nazivamo konačni elementi. Elementi su međusobno povezani u točkama koje nazivamo čvorovi. Za svaki element se pretpostavlja rješenje zadane diferencijalne jednadžbe. Diferencijalne jednadžbe imaju oblik interpolacijskih funkcija koje povezuju zavisne varijable s njihovim vrijednostima u čvorovima. Za svaki element se izvodi lokalni algebarskih jednadžbi čije su nepoznanice čvorne veličine. Nakon toga se odgovarajućim postupcima formira globalni sustav jednadžbi za cijeli diskretizirani model, u kojemu su nepoznanice čvorne vrijednosti svih elemenata diskretiziranog područja.

Razlikuju se jednodimenzijski, dvodimenzijski i trodimenzijski konačni elementi. Također, postoje elementi za rješavanje posebnih geometrijskih oblika poput pločastih i ljuskastih elemenata, no oni neće biti predstavljeni u ovom radu.

Korištenje metode konačnih elemenata, kao i mnoge druge numeričke metode, omogućuju izbjegavanje integriranja koje je računski vrlo zahtjevno, a ponekad i nemoguće izvesti eksplicitno. Ono što metodu konačnih elemenata čini vrlo povoljnim za probleme unutar računalne grafike je što se jednadžbe konačnih elemenata mogu zapisati u obliku velike matrice koja sadrži globalnu jednadžbu konačnih elemenata. Matrice su iznimno povoljne za implementaciju paralelizma, čijom primjenom rješavamo vječni problem računalne grafike, a to su resursi.


Metoda konačnih razlika

Metoda konačnih razlika je numerička metoda koja pomoću jednadžbi konačnih razlika aproksimira derivacije elemenata unutar diferencijalnih jednadžbi. Metoda se zasniva na aproksimaciji formule za derivaciju funkcije

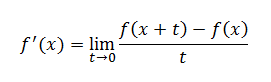
Vrijednost t se zamjenjuje proizvoljnim, dovoljno malim parametrom t te se dobiva aproksimacija zadana u


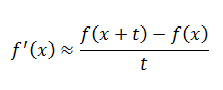
Metoda konačnih volumena

Metoda konačnih volumena je numerička metoda za aproksimaciju diferencijalnih jednadžbi pomoću jednadžbi na sličan način poput metode konačnih elemenata i metode konačnih razlika. Volumen se dijeli na velik broj manjih volumena koji okružuju svaki čvor na Lagrangeovoj mreži. Volumni integrali u parcijalnoj diferencijalnoj jednadžbi pretvoreni su u integrale po površini koristeći Gaussov teorem divergencije. Zatim se izračunavaju tokovi, primjerice energije ili sile iz jednog volumnog elementa u susjedni. Na temelju tokova mogu se odrediti vrijednosti čvorova. Metoda je povoljna za nedovoljno dobro strukturirane mreže, pa se često koristi pri izračunavanju problema kod dinamike fluida.


Metoda konačnih granica

Metoda konačnih granica je zanimljiva alternativa rješavanju diferencijalnih jednadžbi pomoću metode konačnih elemenata, kada se o elementima razgovara kao trodimenzionalnim entitetima. Umjesto da se element gleda kroz njegov volumen, slično kao i kod metode konačnih volumena, svi izračuni se obavljaju na površini elementa. Time se problem iz tri dimenzije spušta na problem dvije dimenzije. No, ovakav pristup moguć je samo za elemente koji se sastoje od homogenog materijala. Također, topološke promjene objekta, poput lomova, teško se implementiraju, odnosno zahtijevaju veće promjene u postojećem matematičkom modelu.