3D skeneri obično generiraju veliku količinu podataka o
geometriji i atributima objekta. Geometrijski
podaci opisuju oblik i dimenzije objekta, dok
atributi opisuju svojstva povrine kao to su
boja, koordinate tekstura, temperaturu i sl.
Vierezolucijski prikaz (ili analiza) efikasan
je način za predstavljanje skupa podataka pri
različitim razinama razlučivosti. U takvom
prikazu početni skup podataka rastavlja se u niz
aproksimacija i niz detalja. Svaka pojedina
aproksimacija predstavlja početni skup podataka
na pojedinoj razlučivosti. Skup detalja biljei
podatke izgubljene pri pojedinoj aproksimaciji.
Glavna prednost vierezolucijskog prikaza je
efikasnost u prikazu kao i računalna efikasnost.
Vierezolucijski prikaz viefunkcionalan je alat
i ima mnogobrojnu primjenu kao to su
kompresija, uklanjanje uma, editiranje i sl.
Algoritmi opisani u ovom poglavlju koriste progresivne
mree s ograničenim kolapsiranjem bridova za
frekvencijsku dekompoziciju. Ideju
vierezolucijskog prikaza pomoću progresivnih
mrea prvi put je predstavio Hugues Hoppe iz
Microsofta na Siggraphu '96 [Hoppe96].
Modeli u računalnoj grafici vrlo često su
prikazani upotrebom mree trokuta. Geometrijski
to je glatka linearna struktura koja se sastoji
od trokuta spojenih zajedničkim bridovima.
Detaljni modeli predstavljeni na ovaj način mogu
se sastojati od stotina tisuća trokuta, pa je
zbog njihove veličine takve modele vrlo
problematično i vremenski zahtjevno prikazivati
ili prenositi preko računalne mree.
U rjeavanju ovog problema Hoppes je predloio
takvu optimizaciju mree u kojoj bi se
proizvoljna mrea M pohranila kao mnogo
grublja mrea M0
zajedno s nizom od n zapis kako postepeno
poboljati mreu M0 točno do
razine početne mree M= Mn.
Svaki od tih zapisa sadri podatke povezane
podjelom vrhova (engl. vertex split),
elementarnom operacijom koja u mreu dodaje
jedan novi vrh. Takav prikaz naziva se
progresivna mrea (PM).
Moemo, prema tome, mreu M u PM
reprezentaciji zapisati kao niz mrea M0,
M1, M2,..., Mn
sve veće točnosti.
Da bi se proizvoljna mrea M pohranila u
progresivnom obliku, koristi se topoloka
transformacija koja se naziva kolapsom brida (edge
collapse).
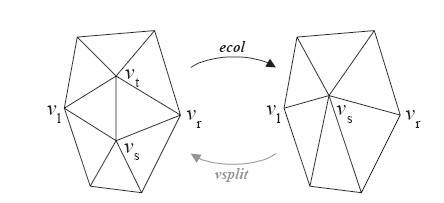
Slika 3-4.
Ilustracija
kolapsa brida.
Kao to se vidi na slici 3-4 transformacija
kolapsa brida ecol ({vs, vt}),
spaja dva susjedna vrha vs
i vt u
jedinstveni vrh vs.
vrh vt, a dva susjedna
trokuta {vs, vt, vl}
i {vt, vs, vr}
u toku procesa nestanu. Za novi, jedinstveni
vrh vs odredi se nova
lokacija. Prema tome inicijalnu mreu M =Mn
moemo pojednostaviti kroz niz od n
sukcesivnih kolapsa bridova:


Konkretan izbor redoslijeda kolapsa bridova
treba paljivo odabrati, kako bi aproksimacije u
pojedinim koracima (Mi, i<n)
bile to kvalitetnije.
Ključna činjenica je da je operacija kolapsa
brida reverzibilna. Inverzna operacija naziva se
podjela vrhova (vrh split), koja je
također prikazana na slici 3-4 podjela vrhova
vsplit(s,l,r,t,A) u blizinu
zajedničkog vrhova vs dodaje
novi vrh vt i dva nova trokuta
{vs, vt, vl}
i {vt, vs, vr}.
Ovakva transformacija također prepravlja
atribute mree u okolici transformacije (npr.
poziciju vrhova vs i
eventualne diskretne i skalarne atribute mree
kao to su normale, koordinate tekstura i sl.).
Sada
moemo prikazati mreu M kao jednostavnu
mreu M0 i niz od n vsplit
zapisa:

Oblik (M0,
{vsplit0,..., vsplitn-1})
naziva se progresivni oblik mree M.
Na slici 3-5 dan je
primjer PM zapisa jedne proizvoljne mree
M.

Slika 3-5. PM zapis proizvoljne mree M. Modeli
imaju (slijeva na desno) 150, 500, 1000 i 13500
trokuta.
Praun-Hoppeov algoritam
Osnovni uvjet da bi algoritam bio robustan, je
da se vodeni ig pohrani to dublje u sam
sadraj objekta. Ideja ovog algoritma je da uz
zadanu proizvoljnu mreu trokuta
v=(v1,...vn)T
i zadani vodeni ig
w=(w1...
wm)T
omogućimo da svaki od koeficijenata iz vodenog
iga wi
izazove mali pomak određenog podskupa
vrhova. Taj pomak postie se generalizacijom
opisane ideje rasprenog spektra. Za
svaki koeficijent wi vodenog
iga, konstruira se po jedna skalarna funkcija
baze
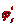 . Tijekom proces umetanja
vodenog, cilj je da se vrh vj
pomjeri za vektor proporcionalan s
wi
. Tijekom proces umetanja
vodenog, cilj je da se vrh vj
pomjeri za vektor proporcionalan s
wi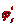 di,
pri čemu je di
vektor smjera pomaka, određen kao
normala iz vrha cj. Osnovni
problem je kako odrediti bazne funkcije
Φ=(φ1
φm).
di,
pri čemu je di
vektor smjera pomaka, određen kao
normala iz vrha cj. Osnovni
problem je kako odrediti bazne funkcije
Φ=(φ1
φm).
Da bi cjelokupni
ovakav model zatite vodenim igom bio robustan,
bazne funkcije Φ moraju korespondirati vizualno
značajnim odlikama modela, iz razloga opisanih u
uvodu u ovo poglavlje. Kao to je već rečeno,
kod 2D objekata to su DCT koeficijenti s
najvećom amplitudom.
Pristup s
progresivnim mreama previđa da se odredi m
kolapsa (odnosno m split operacija)
koji uzrokuju najvidljivije promjene na modelu,
odnosno najveću promjenu geometrije modela i te
promjene označimo kao najvanije. Za svaku takvu
promjenu definira se po jedna bazna funkcija s
područjem djelovanja na cijelom susjedstvu
pripadajućeg vrhova u mrei M. Tih m
baznih funkcija se tada upotrijebi za
umetanje vodenog iga od m članova.
Prvi korak
algoritma je da se zadana mrea M
pojednostavi prebacivanjem u PM prikaz,
primjenom niza ograničenih kolapsa bridova. U
svakoj takvoj operaciji po jedan brid se
pretvara u jednu od svojih krajnjih točaka, kao
to je prikazano na slici 3-6.
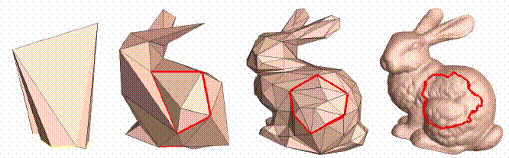
Slika 3-6. Prikazan je niz pojednostavljenja
modela upotrebom kolapsa bridova. Crvenim
obrubom prikazano je isto područje na modelima s
različitim brojem bridova.
Veličinu promjene modela h nastale u
pojedinoj operaciji podijele vrhova određujemo
na način da predvidimo lokaciju na kojoj bi se
mogao pojaviti novi vrh i onda izračunamo
veličinu proporcionalnu udaljenosti predviđene i
stvarne lokacije novog vrhova. Predviđenu
lokaciju računamo kao koordinate centroida
neposrednih susjeda vrhova koji se dijeli. Nakon
toga izračunamo normalu na trokut u kojem se
nalazila predviđena lokacija i konačno h
izračunamo kao skalarni produkt vektora normale
i vektora udaljenosti između predviđene i
stvarne lokacije.
Nakon to smo odredili m podjela vrhova s
najvećim h, moemo konstruirati m
pripadajućih baznih funkcija φi.
Budući da se koristi ograničeni kolaps bridova,
svaki vrh ci koji se počne
dijeliti u konačnici je povezan s skupom bridova
u izvornoj mrei M koji su nastali zbog
podijele tog vrhova i novih vrhova nastalih iz
njega.
Susjedstvo Bi
pripadajućeg vrhova ci određujemo
kao prsten rubova oko vrhova ci koji
se određuje tako da pratimo kako se ire
neposredni bridovi vrha ci
tijekom postupka:
 .
.
Na slici 3-6 crvenim rubom označeno je
susjedstvo vrha ci u pojedinim
koracima gore naznačenog postupka.
Susjedstva pojedinih baznih funkcija mogu se
preklapati, kao to je to vidljivo na slici 3-7
gdje prikazan model s 50 baznih funkcija.

Slika 3-7. susjedstva nad kojima su definirane
funkcije φi.
U svakom susjedstvu konstruira se radijalno
simetrična bazna funkcija. Za početak, mora se
odrediti funkcija radijusa
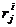 za svaki vrh vj,
takva da preslikava sredinji vrh ci
u 0, a vrhove s granice Bi u
1, dok između linearno raste. Preciznije, za
svaki vrh vj definiramo
funkciju preslikavanja u relativni radijus:
za svaki vrh vj,
takva da preslikava sredinji vrh ci
u 0, a vrhove s granice Bi u
1, dok između linearno raste. Preciznije, za
svaki vrh vj definiramo
funkciju preslikavanja u relativni radijus:
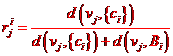
Pri tome je d(v, S) duljina
najkraćeg puta između vrha v i bilo kojeg
drugog vrha iz skupa S.
Udaljenosti d(vj, {ci})
i d(vj,Bi)
mogu se lagano izračunati primjenom
Dijkstrinog algoritma na bridove mree.
Dvije su bitne odlike vane kod konstrukcije
baznih funkcija. Kao prvo promjene izazvane na
3D objektu ne bi smjele biti vizualno uočljive i
kao drugo ne bi se smio mijenjati volumen
objekta (to bi značilo da se dio objekta
skalirao u nekom smjeru).
Kako su poligonalne mree i same po
sebi C0 kontinuiteta, nije
potrebno da bazna funkcija bude primjerice n
kontinuirana, ali iskustveno je utvrđeno da
ljudsko oko vrlo dobo zamjećuje diskontinuitete
derivacija, tako da funkcije koje nemaju barem C1
kontinuitet izazivaju vidljive distorzije na
modelu. Da bi se eliminirali te te
diskontinuitete moe se upotrijebiti polinom
trećeg stupnja
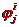 =2*r3-3*r3+1
koji ima oblik polucilindra (slika 3-8).
=2*r3-3*r3+1
koji ima oblik polucilindra (slika 3-8).
Kako je na početku postavljeno jo jedno
ograničenje da bazna funkcija ne smije mijenjati
volumen objekta, integral funkcije unutar
radijusa
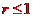 mora biti 0. To rezultira
funkcijom koja liči na sombrero. Da bi se takva
funkcija izgladila, postavljen je dodatni uvjet
da druga derivacija u vrhu bude 0, čime je
dobiven konačni oblik funkcije
mora biti 0. To rezultira
funkcijom koja liči na sombrero. Da bi se takva
funkcija izgladila, postavljen je dodatni uvjet
da druga derivacija u vrhu bude 0, čime je
dobiven konačni oblik funkcije
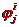 =-21*r5 + 45*r4
25*r3 +1. Sve tri
funkcije i njihovo djelovanje na vrhove unutar
relativnog radijusa r prikazane su na
slici 3-8.
=-21*r5 + 45*r4
25*r3 +1. Sve tri
funkcije i njihovo djelovanje na vrhove unutar
relativnog radijusa r prikazane su na
slici 3-8.
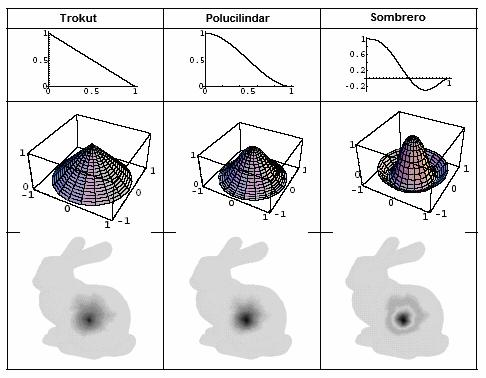
Slika 3-8 Moguće bazne funkcije i njihovo
djelovanje na model.
Slika 3-9. Pomak svakoj pojedinog vrha vj
određen je zajedničkim utjecajem svih baznih
funkcija unutar čijih se dosega nalazi vrh.
(odnosno ako su unutar relativnog radijusa
manjeg ili jednakog 1).
Svaka bazna funkcija mnoi se pripadnim koeficijentom wi
iz vodenog iga. Koeficijenti wi su
realni brojevi, dobiveni slučajno odabrani po
normalnoj razdiobi s srednjom vrijednoću 0 i
standardnim odstupanjem (varijancom) 1.
U matričnom zapisu,
umetanje vodenog iga moemo zapisati ovako (za
X koordinatu):
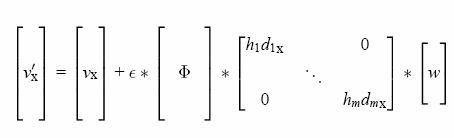
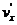 su X koordinate
dobivene nakon umetanja vodenog iga.
su X koordinate
dobivene nakon umetanja vodenog iga.
vx su X
koordinate vrha v u nemodificiranom
(izvornom) objektu.
ε je korisnički zadan parametar koji slui za
skaliranje energije vodenog iga.
Φ je n x m matrica čiji su stupci
skalarne funkcije φi
hidix
je m x m dijagonalna matrica čiji
su elementi X komponente vektora smjera di,
skalirane veličinom bazne funkcije hi
koja određuje veličinu utjecaja pojedine bazne
funkcije
w je vektor stupac vodenog iga
Ako konkateniramo matrice za sve prostorne
komponente (X,Y,Z) proces umetanja vodenog iga
moemo opisati matričnom jednadbom:
v' = v + B w
Izvorni model w, zajedno s vodenim
igom w¸ pohrani se na sigurno
mjesto, a dokument v'
sa umetnutim vodenim igom se objavi.
Prije nego to pokuamo dohvatiti vodeni ig iz
sumnjivog dokumenta, moramo obadva dokumenta
postaviti u isti koordinatni prostor (i prema
potrebi ponovno uzorkovati kako bi dobili model
s geometrijom modela koji ispitujemo i
topologijom naeg originalnog dokumenta).
Upotrebom istog skupa baznih funkcija tj. matrice B, iz gornje
jednadbe kojom je opisano umetanje vodenog iga
dobivamo :
B w*
=(v*-v)
Izraz na desnoj strani ove jednakosti opisuje pomak vrhova
sumnjivog modela u odnosu na na originalni
dokument. Rjeavanjem te jednadbe dobivamo
koeficijente w* koje
usporedimo s koeficijentima w naeg
pohranjenog vodenog iga.
KangKangov algoritam vrlo je sličan Praunovom modelu, ali se
bazira na Burt-Adelsonovoj piramidi. B-A piramida
je piramidalna shema koju su razvili Burt i
Adelson [Burt83] za saeto kodiranje slika, a
Guskov [Guskov99] ju je prilagodio mreama trokuta
definiranjem neuniformnog operatora relaksacije.
3D relaksacija povrine mree je operacija koja pomiče vrhove
3D mree kako bi minimizirala energetsku funkciju
takve mree. Ta operacija vrlo je često koritena
u postupcima zaglađivanja 3D modela, jer se
operatorom relaksacije minimizira zakrivljenost
mree i dobiva glatki objekt. U Burt-Adelsonovoj
mrenoj piramidi operator relaksacije koristi se
za konstrukciju neuniformne sheme kojom se
generiraju glatke aproksimacije izvorne mree.
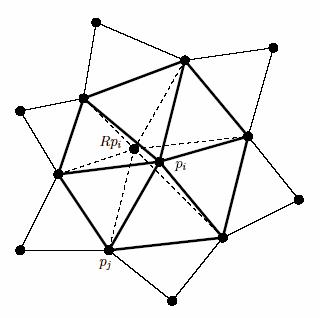
Slika 3-10. SOD relaksacija vrha pi.
Na slici se vidi izgled proirenog susjedstva vrha
pri operaciji SOD relaksacije.
Guskov je opisao neuniformni operator relaksacije koji
minimizira diferenciju drugog reda D2e
svakog brida e u mrei. Zbog toga
je uobičajeni naziv za ovu vrstu relaksacije SOD
(engl. second order differences)
relaksacija. Ako je poloaj vrha vi
zadan s pi = {x, y, z}
tada će poloaj relaksiranog vrha Rpi
biti izabran na način da je
|
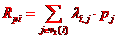 uz uz
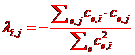
|
Pri tome je v2(i)
proireno prstenasto susjedstvo 1 reda oko vrha
vi kako je to prikazano na slici
3.10. 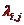 su teinski koeficijenti
operatora relaksacije, a koeficijenti
su teinski koeficijenti
operatora relaksacije, a koeficijenti
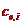 o poloaju vrha vi
o poloaju vrha vi

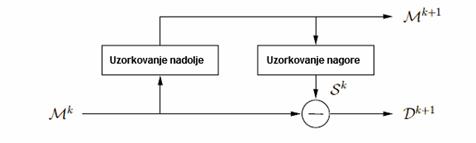
Slika 3-11. Vierezolucijski prikaz upotrebom
Burt-Adelsonove piramide
Vierezolucijska shema bazirana na
Burt-Adelsonovoj piramidi započinje od najfinije
mree M0 iz koje se računa
sekvenca mrea Mk (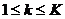 ) kao i razlika između mrea
Dk. Razina rezolucije određena je
parom (Mk, Dk),
osim za najfiniju mreu M0.
Dekompozicija se sastoji od 3 koraka:
) kao i razlika između mrea
Dk. Razina rezolucije određena je
parom (Mk, Dk),
osim za najfiniju mreu M0.
Dekompozicija se sastoji od 3 koraka:
-
Simplifikacija: U ovom koraku se
inicijalna mrea, uklanjanjem određenih vrhova,
uzorkuje nanie (engl. downsampling) u
grublju mreu Mk+1. Za grublju
mreu Mk+1 kaemo da je
aproksimacija inicijalne mree Mk.
-
Podjela: U ovom koraku se grublja
mrea Mk+1umetanjem prethodno
uklonjenih vrhova i relaksacijom svih vrhova
uzorkuje navie (engl. upsamling),
čime se dobiva aproksimacija Sk
inicijalne mree M0.
-
Izračun detalja: U ovom se
koraku proračunavaju razlike u mrei Mk
i mrei Sk čime se
dobivaju koeficjenti Dk+1
vezani za mreu Mk+1.
Detalji se računaju za svaki vrh mree Mk.
Rekonstrukcija se izvodi obrnutim izvođenjem
gornje sheme: započinjemo od grublje mree Mk+,
podijelimo ju i dodamo detalje Dk+1
kako bi rekonstuirali finiju mreu Mk.
Glavni korak ovakvog vierezolucijskog prikaza je uzorkovanje
nadolje kojim se iz mree izbacuje neovisni skup
vrhova (vrhova koji međusobno nisu povezani
zajedničkim bridom). Ovu metodu osmislio je
Kobbelt [Kobbelt98] za potrebe njegovog
vierazinskog algoritma zaglađivanja. Vrhovi koji
će biti maknuti nizom kolapsa bridova nazivaju se
neparni vrhovi. Kako bi se stvorila glatka
aproksimacija u svakom koraku se izvodi
relaksacija vrhova. Skup neparnih vrhova koji će
biti izbačeni moe se odrediti na različite
načine, ali se u konkretno slučaju koristi
Garlandova kvadratna metrika [Garland97], kojom se
zadravaju vizualno najuočljivija svojstva mree.
Sam postupak umetanja vodenog iga, nakon to je konstruirana
B-A piramida i odabrana grublja mrea eljenog
stupnja, sličan je metodi koju koristi Praun.
Glavna razlika je u tome to Praun et al.
najznačajnije komponente za umetanje vodenog iga
nalazi prateći niz kolapsa bridova i odabirući one
u kojima je poloaj novog vrha najtee
predvidjeti, dok se ovdje vodeni ig umeće izravno
u jednu od grubljih mrea iz B-A piramide, nakon
čega se piramida izvrće i rekonstruira se fina
mrea. Na taj način kod KangKangovog modela
energija umetnuta u vrhove grube mree iri se u
finijim mreama u svoju okolinu. Taj postupak
naziva se vierezolucijsko uređenje (engl.
multiresolution edit).