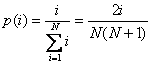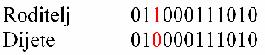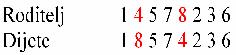Sadržaj
1.
Uvod
2.
Genetski
algoritmi
2.1.
Općenito o genetskim algoritmima
2.2.
Generiranje početne populacije
2.3.
Funkcija cilja (Fitness function)
2.4.
Selekcija
2.4.1.
Jednostavna selekcija
2.4.2.
Linearno sortirajuća selekcija
2.4.3.
K-turnirska selekcija
3.
Prikazi
rješenja
3.1.
Binarni
prikaz
3.2.
Prikaz
permutiranim nizom
3.3.
Matrični prikaz
4.
Genetski
operatori
4.1.
Križanje (Crossover)
4.1.1.
Križanje sa k točaka prekida
4.1.2.
PMX
križanje (Partially Matched Crossover)
4.1.3.
Pohlepno križanje (Greedy Crossover)
4.1.4.
GSX
križanje (Greedy Subtour Crossover)
4.2.
Mutacija
4.2.1.
Jednostavna mutacija
4.2.2.
Miješajuća mutacija
4.2.3.
Pohlepna zamjenska mutacija (Greedy Swap Mutacija)
4.2.4.
2opt
metoda
5.
Primjena
genetskih algoritama
5.1.
Problem
trgovačkog putnika
5.1.1.
Definicija problema
5.1.2.
Pokusi s parametrima
5.1.3.
Ovisnost vremena izvođenja i kvalitete rješenja o veličini populacije
5.1.4.
Ovisnost vremena izvođenja i kvalitete rješenja o vjerojatnosti križanja
5.1.5.
Ovisnost vremena izvođenja i kvalitete rješenja o vjerojatnosti mutacije
5.1.6.
Usporedba kombinacija selekcije, križanja i mutacije
5.2.
Problem
n-kraljica
5.2.1.
Definicija problema
5.2.2.
Pokusi s parametrima
5.2.3.
Ovisnost broja generacija o veličini populacije
5.2.4.
Ovisnost broja generacija o vjerojatnosti križanja
5.2.5.
Ovisnost broja generacija o vjerojatnosti mutacije
5.3.
Zanimljivi primjeri primjene genetskih algoritama
5.3.1.
Portretiranje osumnjičenika
5.3.2.
Sudoku
5.3.3.
Mastermind
6.
Zaključak
7.
Literatura
8.
Sažetak
Evolucija je
neprekidan proces u kojem se živa bića prilagođavaju uvjetima u kojima žive.
Njene temelje opisao je Charles Darwin u 19. stoljeću. U prirodi opstaju one
jedinke koje se najbolje uspijevaju prilagoditi novim uvjetima u okolini, a
one najslabije umiru. Ta neprekidna borba za opstanak naziva se prirodna
selekcija. Svaka se jedinka može opisati nizom svojstava. Jedinke s dobrim
svojstvima imaju veću mogućnost razmnožavanja te tako dobra svojstva imaju
veću mogućnost da se prenesu na slijedeću generaciju.
Svojstva svake jedinke
zapisana su u kromosomima. To su strukture koje nastaju zgušnjavanjem
kromatina za vrijeme stanične diobe, a izgrađene su od nakupina DNK (gena) i
bjelančevina. Strukturu kromosoma otkrili su Watson i Creek 1953. godine.
DNK se sastoji od dvije spiralne niti međusobno povezane dušičnim bazama.
Dušične baze su nositelji informacije u molekuli DNK.
Slika 1‑1
molekula DNK
Istražujući stanične
automate, doktor John Henry Holland (poznat kao otac genetskih algoritama) i
njegovi kolege na Michiganskom sveučilištu došli su na ideju kako bi
prirodne procese mogli iskoristiti u rješavanju nekih problema koje
standardne determinističke metode nisu mogle riješiti. Takvi programi koji
oponašaju evolucijske procese u prirodi nazvani su genetskim algoritmima.
Istraživanja na području
genetskih algoritama bila su uglavnom samo teoretska sve do sredine 80-ih
godina, kada je na Sveučilištu u Illinoisu održana Prva Međunarodna
Konferencija o Genetskim Algoritmima. Na sve veće zanimanje za genetske
algoritme utjecalo je pojačanje snage procesora i ostalih kompjuterskih
komponenti, što je omogućilo i sve veću praktičnu primjenu te metode.
Danas genetski algoritmi
imaju široku primjenu, no njihove mogućnosti još uvijek nisu do kraja
istražene. Mnoga istraživanja danas bave se optimiranjem genetskih
algoritama kako bi radili brže te kako bi njihova rješenja bila što točnija.
U ovom radu opisano je
načelo rada genetskih algoritama, operatori i parametri koji se koriste u
rješavanju problema. Na dva problema, za čije se rješavanje koriste genetski
algoritmi, vršenjem raznih pokusa pokazano je kako parametri utječu na
brzinu izvođenja i točnost rješenja.
Genetski algoritmi
pripadaju metodama usmjerenog slučajnog pretraživanja prostora rješenja (eng.
guided random search techniques). To je heuristička metoda optimiranja koja
imitira prirodni evolucijski proces i primjenjuje ga na apstraktne jedinke.
Snaga ovih algoritama, u odnosu na tradicionalne determinističke metode, je u
mogućnosti određivanja globalnog optimuma u prostoru s više lokalnih optimuma.
No, za razliku od determinističkih metoda, ova stohastička metoda ne garantira
pronalaženje globalnog optimuma.
U rješavanju problema genetskim
algoritmom postoje dva pristupa:
- prilagoditi problem
genetskom algoritmu
- prilagoditi genetski
algoritam problemu
Prilagođavanje genetskog
algoritma problemu najčešće se sastoji od odabira prikladnog prikaza rješenja te
definiranja genetskih operatora pogodnih za taj prikaz.
Problem koji se treba riješiti
predstavlja okolinu u kojoj živi neka populacija. Svaka jedinka (kromosom)
predstavlja potencijalno rješenje, a u računalu je prikazana nekom podatkovnom
strukturom, što je vrlo slično genetskoj šifri živog organizma. Svojstva jedinki
opisuju s ocjenom kvalitete koja se naziva dobrota jedinke, a govori nam koliko
je ta jedinka blizu traženog rješenja.
Na početku algoritma generira
se početna populacija jedinki. Zatim se odabire nekoliko jedinki iz populacije
(selekcija) te se na njih primjenjuju genetski operatori (križanje i mutacija).
Cijeli postupak se ponavlja dok se ne nađe optimalno rješenje ili dok nije
zadovoljen neki od uvjeta zaustavljanja algoritma. Neki od uvjeta zaustavljanja
algoritma mogu biti:
-
zadani broj iteracija (generacija)
-
dostignuta vrijednost funkcije cilja
-
broj iteracija bez poboljšanja
-
vremensko ograničenje

Slika 2‑1 Princip rada genetskih algoritama
Za rješavanje težih
optimizacijskih problema koriste se paralelni genetski algoritmi. Teži problemi
zahtijevaju velike populacije i duljine kromosoma, zbog čega postupak
optimiranja duže traje. U osnovnoj strukturi genetskog algoritma moguće je
izdvojiti neke dijelove koji se mogu izvršavati neovisno, pa je razvojem
višeprocesorskog računala stvorena mogućnost da se ti neovisni dijelovi
paraleliziraju. Time genetski algoritmi dobivaju na brzini.

Slika 2‑2
Postupak stvaranja genetskog algoritma
U daljnjem tekstu bit će opisane neke vrste prikaza
rješenja, selekcije, križanja i mutacije koje se često koriste u rješavanju
Problema trgovačkog putnika i Problema n-kraljica.
Najčešće se početna
populacija generira slučajnim odabirom rješenja iz domene, a moguće ju je
generirati i uniformno (sve jedinke su na početku jednake). Svaka od tih metoda
ima i neke nedostatke. Slučajnim odabirom rješenja može se dogoditi da su neka
rješenja nevaljana pa je potrebno posebno ispitivati uvjet valjanosti. Kod
uniformnog generiranja jedinki problem je u tome što je algoritam u prvih par
generacija neefikasan jer nema puno različitosti među jedinkama. Postoji još
jedna mogućnost generiranja populacije, a to je da se na početku usadi početno
rješenje dobiveno nekim drugim optimizacijskim algoritmom.
Funkcija cilja ili
funkcija dobrote je funkcija čija je uloga ocjenjivanje kvalitete pojedine
jedinke. Ona je ključ za proces selekcije. Što je jedinka kvalitetnija, to je
veća vjerojatnost da će preživjeti, i sudjelovati u križanju te tako stvoriti
potomstvo koje će naslijediti njene dobre gene. Funkcija dobrote treba dobro
odražavati problem koji se rješava pa se određivanje funkcije dobrote smatra
jednim od najvećih poteškoća prilikom definiranja problema i stvaranja algoritma
koji će ga rješavati.
Ukupna dobrota populacije D
definirana je formulom:
A prosječna dobrota populacije
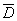 formulom:
formulom:
|
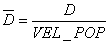 |
(2.2) |
Selekcija je
proces u kojem se odabiru jedinke koje će sudjelovati u reprodukciji i tako
prenijeti svoja svojstva na jedinke slijedeće generacije. Bolje jedinke trebaju
imati veću vjerojatnost razmnožavanja, no loše jedinke ne treba potpuno
isključiti jer i one mogu sadržavati neke dobre gene. Kako bi se najbolje
jedinka očuvala iz generacije u generaciju uvodi se postupak elitizma te se
najbolje jedinka prenosi u slijedeću generaciju nepromijenjena.
Prema načinu prenošenja
genetskog materijala boljih jedinki u slijedeću generaciju selekcije se dijele
na:
1.
generacijske selekcije
2.
eliminacijske selekcije
Generacijskom selekcijom
direktno se biraju bolje jedinke koje će kasnije sudjelovati u reprodukciji te
se kopiraju u novu populaciju (međupopulaciju). Kako je broj jedinki u
međupopulaciji manji od veličine populacije, najčešće se međupopulacija
popunjava duplikatima preživjelih jedinki. Na jedinke međupopulacije se
primjenjuju genetski operatori te se tako stvara nova generacija. Ova vrsta
selekcije ima dva nedostatka. Prvi nedostatak je stvaranje međupopulacije jer se
u radnom spremniku odjednom nalaze dvije populacije. Drugi nedostatak je
mogućnost pojave duplikata u slijedećoj iteraciji jer duplikati ne pridonose
kvaliteti dobivenog rješenja.
Kod eliminacijskih selekcija
briše se M jedinki s lošim svojstvima, a izbrisane jedinke se nadomještavaju
jedinkama koje se dobiju u reprodukciji. Parametar M se zove mortalitet. Ovom
selekcijom se uklanjaju oba nedostatka generacijske selekcije.
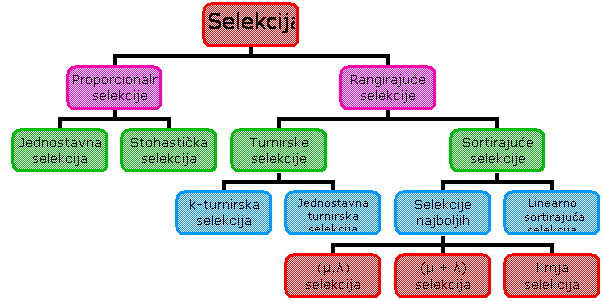
Prema načinu odabira jedinki
selekcije se dijele na:
- proporcionalne selekcije
- rangirajuće selekcije
Kod proporcionalnih selekcija
vjerojatnost selekcije ovisi o umnošku dobrote jedinke i prosječne dobrote
populacije, tj. vjerojatnost selekcije je proporcionalna s dobrotom jedinke.
Rangirajuće selekcije odabiru
jedinke s vjerojatnošću koja ovisi o položaju jedinke u poretku jedinki
sortiranih po dobroti. Ova vrsta selekcija dijeli se na turnirske i sortirajuće
selekcije.
Slika 2‑3 Vrste selekcija
Jednostavna
selekcija često se uspoređuje s kotačem ruleta. Vjerojatnost odabira pojedine
jedinke ovisi o njenoj dobroti.
Postupak selekcije provodi se u
4 koraka:
- izračunaju se dobrote svih
jedinki u populaciji
- izračuna se ukupna dobrota
populacije
- za svaku jedinku se
izračuna kumulativna dobrota prema izrazu:
|
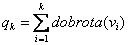 |
(2.3) |
tako da vjerojatnost selekcije za pojedinu jedinku iznosi pk:
|
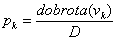 |
(2.4) |
- generira se slučajni
realni broj
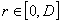 i
potraži se i-ti kromosom za koji vrijedi da je
i
potraži se i-ti kromosom za koji vrijedi da je
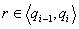 te
se taj kromosom prenosi u slijedeću generaciju.
te
se taj kromosom prenosi u slijedeću generaciju.

Slika 2‑4
Kumulativna dobrota qi i vjerojatnost selekcije jedinki pi
Jednostavna selekcija ima
nekoliko nedostataka. Budući da je vjerojatnost odabira proporcionalna dobroti
jedinke, funkcija dobrote ne smije poprimati negativne vrijednosti. Taj se
nedostatak rješava tako da se definira nova funkcija dobrote koja od vrijednosti
dobrote za svaku jedinku oduzme minimalnu vrijednost dobrote u cijeloj
populaciji. Nedostaci su još i mogućnost pojavljivanja duplikata i neefikasnost
kod malih razlika u dobroti jedinke.
Kod linearno
sortirajuće selekcije vjerojatnost odabira proporcionalna je poziciji jedinke u
poretku jedinki sortirani prema dobroti. Vjerojatnost selekcije računa se prema
formuli:
|
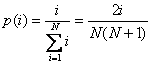 |
(2.5) |
(najbolja jedinka ima indeks N,
a najgora indeks 1)
K-turnirska
selekcija u svakom koraku s jednakom vjerojatnošću odabire k jedinki iz
populacije i od njih odabere najbolju koja će dalje sudjelovati u reprodukciji.
No, ova se vrsta selekcije najčešće koristi na drugi način. Od k izabranih
jedinki biraju se najbolje dvije i na njih se onda primjenjuju genetski
operatori. Prednost ove selekcije je u tome što se dobrota jedinke računa samo
za nove jedinke i nema potrebe za sortiranjem čime se znatno dobiva na brzini.
Druga prednost je mogućnost
paraleliziranja procesa selekcije i reprodukcije jer je moguće paralelno
izvoditi par turnirskih selekcija nad nekom populacijom.
Svi podaci koji
opisuju jedinku zapisani su u kromosomu. Kromosom može biti bilo kakva struktura
podataka koja opisuje sva potrebna svojstva. Način na koji su ti podaci kodirani
može jako utjecati na brzinu rada i točnost rješenja, pa je zbog toga bitno
odabrati strukturu podataka primjerenu za problem koji rješavamo. Za odabrani
prikaz rješenja potrebno je definirati i genetske operatore.
Postoji mnogo različitih načina
na koji se mogu kodirati podaci u kromosomu, te je svaki način prikladan za
određenu skupinu problema. Za problem optimiranja funkcija najčešće se koriste
binarni prikaz i prikaz realnim brojevima, a osim njih koriste se i nizovi
brojeva, polja, binarna stabla itd.
Prikaz binarnim
kodom najčešći je prikaz rješenja jer se u praksi pokazalo da daje najbolje
rezultate u većini problema u čijem se rješavanju koristi. Uz njega je vezana
većina teorije o genetskim algoritmima.
U binarnim prikazu kromosom je
prikazan nizom bitova i predstavlja binarnu vrijednost broja
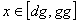 .
Duljina n binarnog broja označava broj bitova u binarnom broju i utječe
na preciznost. U vektor duljine n moguće je zapisati 2n
različitih kombinacija nula i jedinica, tj. bilo koji broj iz intervala [0,2n-1].
Vektor v(0) predstavlja broj x=dg, a vektor v(2n-1)
predstavlja vrijednost x=gg.
.
Duljina n binarnog broja označava broj bitova u binarnom broju i utječe
na preciznost. U vektor duljine n moguće je zapisati 2n
različitih kombinacija nula i jedinica, tj. bilo koji broj iz intervala [0,2n-1].
Vektor v(0) predstavlja broj x=dg, a vektor v(2n-1)
predstavlja vrijednost x=gg.
Binarni vektor v(b)=[Bn-1Bn-2...B1B0]
predstavlja binarni broj b:
|
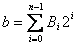 |
(3.1) |
Kodiranje realnog broja x iz
intervala [dg,gg] obavlja se prema formuli:
|
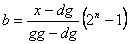 |
(3.2) |
A dekodiranje binarnog broja u
potencijalno rješenje prema formuli:
|
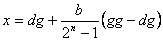 |
(3.3) |
Pri kodiranju brojeva binarnim
prikazom važno je odrediti preciznost rješenja. Neka je za neki interval [dg,gg]
zadana preciznost p (što znači da je rješenje x na točno p decimala). Tada za
preciznost p i duljinu kromosoma n mora vrijediti:
|
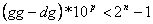 |
(3.4) |
Iz te formule može izvesti
izraz za minimalnu duljinu kromosoma potrebnu za neku određenu preciznost:
|
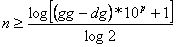 |
(3.5) |
Prikaz permutiranim
nizom koristi se i za rješavanje Problema trgovačkog putnika i N-kraljica. U
prikazu permutiranim nizom ulogu imaju i pozicija određenog broja u nizu i
vrijednost tog broja.
Kod Problema N-kraljica
pozicija broja u nizu označava stupac, a broj predstavlja redak u kojem se
kraljica nalazi, no moguće je i obrnuto.
Kod Problema trgovačkog putnika
pozicija broja označava kada će grad biti posjećen, a broj predstavlja koji je
to grad.
Ovaj prikaz vrlo je pogodan za
rješavanje oba problema jer se može lako provjeriti da li se neki broj u nizu
pojavljuje više puta, što je zabranjeno po definiciji problema. Isto tako, lako
se mogu zamijeniti neki brojevi u nizu ako je to potrebno, a da se ne utječe na
ostale brojeve.
Osim prikaza
permutiranim nizom u rješavanju problema trgovačkog putnika ili n-kraljica može
se koristiti i matrični prikaz.
Kod problema trgovačkog putnika
matrica koja se koristi za prikaz rješenja jest matrica susjedstva. Matrica je
veličine 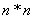 ,
gdje n predstavlja broj gradova. Matrica se gradi tako da se promatraju
parovi gradova. Ako postoji put iz nekog grada A u neki grad B tada je na mjestu
u matrici
,
gdje n predstavlja broj gradova. Matrica se gradi tako da se promatraju
parovi gradova. Ako postoji put iz nekog grada A u neki grad B tada je na mjestu
u matrici 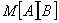 jedinica,
a inače je nula.
jedinica,
a inače je nula.
Kod problema n-kraljica indeksi
u matrici označavaju retke i stupce, a brojevi u matrici označavaju da li se
kraljica nalazi na tom položaju ili ne. Ako se kraljica nalazi na nekom mjestu
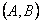 tada
je u matrici
tada
je u matrici 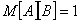 ,
a ako se ne nalazi tada je
,
a ako se ne nalazi tada je 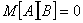 .
.
Matrični prikaz je dosta
kompleksan pa se zato češće upotrebljava prikaz permutiranim nizom.
Genetski operatori
mijenjaju genetski materijal jedinki. Oni djeluju tijekom reprodukcije u kojoj
sudjeluju jedinke koje su preživjele selekciju. Njihova zadaća je da stvore
potomstvo od odabrane populacije roditelja.
Prema načinu djelovanja
operatori se dijele na dvije skupine:
v
operatori višeg reda
v
operatori unarni
Operatori višeg reda djeluju
tako da kreiraju nove jedinke (djecu) kombinirajući genetski materijal
različitih jedinki (roditelja), a unarni operatori vrše slučajnu promjenu dijela
genetskog materijala pojedinačne jedinke.
Genetski operator
križanja je binarni operator koji imitira prirodni proces križanja. U tom
procesu sudjeluju dvije slučajno odabrane jedinke (roditelji). Miješanjem
njihovog genetskog materijala nastaje jedna ili dvije nove jedinke (djeca).
Operacija križanja provodi se sve dok novonastala populacija nije potpuno
popunjena jedinkama.
Kako se selekcijom odabiru
jedinke s dobrim svojstvima, nasljeđivanjem njihovog genetskog materijala djeca
bi također trebala imati dobra (ako ne i bolja) svojstva.
Postoji mnogo vrsta križanja, a
odabir neke od njih ovisi o prikazu rješenja koji se koristi u rješavanju
problema.
Križanje može biti
definirano s proizvoljnim brojem prekidnih točaka.
Najjednostavniji oblik
operatora križanja je križanje s jednom točkom prekida (one-point crossover).
Slučajno se odabere neka točka prekida unutar kromosoma oba roditelja (jednako
udaljena od početka oba roditelja), te se sadržaji kromosoma nakon te točke
zamijene. Time se dobivaju dva potomka.

Slika 4‑1
Križanje s jednom točkom prekida
Križanje s dvije točke prekida
(two-point crossover) obavlja se tako da se odaberu dvije točke prekida unutar
kromosoma koje su za oba roditelja jednake. Sadržaji kromosoma između te dvije
točke se mijenjaju i tako nastaju dva potomka.
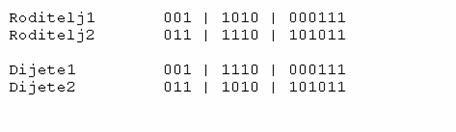
Slika 4‑2
Križanje s dvije točke prekida
Križanje s više točaka prekida
radi se na sličan način, a dijelovi između točaka prekida se naizmjence spajaju.
Krajnji oblik ovog načina križanja je uniformno križanje (uniform crossover) ili
križanje s n-1 prekidnih točaka (n je broj bitova). Prilikom ovog križanja
nastaje samo jedno dijete koje nasljeđuje pojedini gen od roditelja s fiksnom
vjerojatnošću od 0.5%. Ako se vjerojatnost nasljeđivanja razlikuje tada se
križanje naziva p-uniformno križanje. Parametar p određuje kolika je
vjerojatnost da se pojedini gen naslijedi od prvog roditelja, a vjerojatnost da
se naslijedi od drugog roditelja jednaka je 1-p.

Slika 4‑3
Uniformno križanje
U rješavanju nekih
problema, gdje se koristi prikaz rješenja permutiranim nizom, križanje sa jednom
ili više točaka nije dovoljno dobro. Kod takvog križanja, prilikom izmjene
genetskom materijala, velika je vjerojatnost da će se brojevi u nizu ponavljati,
a to nije dopušteno. Zbog toga se koristi križanje koje je vrlo slično križanju
s dvije točke prekida, ali dodatno rješava i problem jednakih brojeva. Takva
vrsta križanja naziva se PMX operator.
U prvom koraku provodi se
obično križanje s dvije točke prekida.

Slika 4‑4 Prvi
korak PMX križanja
U primjeru se vidi da niti
jedan potomak nije pravilan jer se brojevi u nizu ponavljaju. To se rješava tako
da se kromosom svakog djeteta najprije podijeli istim točkama prekida na 3
dijela. Prvi i treći dio su dijelovi koji su se kopirali od jednog roditelja, a
drugi dio je dijete naslijedilo od drugog roditelja. Nakon toga provjerava se da
li je neki broj iz prvog ili trećeg dijela jednak nekom broju u drugom dijelu.
Ako je, tada se taj broj zamjeni s brojem koji se kod prvog roditelja nalazi na
mjestu na kojem se kod djeteta nalazi broj u drugom dijelu za koji se vršilo
pretraživanje.
Na konkretnom primjeru, u prvom
potomku broj 1 pojavljuje se na pozicijama 1 i 5. Kako je broj 1 na poziciji 5
noviji, broj 1 na poziciji 1 zamjenjuje se brojem 8, koji se nalazi na poziciji
5 prije križanja. Sada se broj 8 nalazi na pozicijama 1 i 4, pa se broj 8 na
poziciji 1 zamijeni s brojem 3. Analogno se zamijene svi brojevi koji se u
kromosomima potomaka ponavljaju i dobiju se dva potomka koja zadovoljavaju
uvijete.

Slika 4‑5 Drugi
korak PMX križanja
U eksperimentima se pokazalo da
PMX križanje relativno brzo dolazi do rješenja bliskih optimumu, te populaciju
odvlači lokalnom optimumu, pa je teško doći do konačnog rješenja. Relativna
složenost ovog algoritma je još jedan problem ove vrste križanja. Usprkos tome,
PMX se vrlo često koristi za rješavanje problema n-kraljica.
Pohlepno križanje
koristi se kod rješavanja problema trgovačkog putnika, a bazira se na oponašanju
pohlepnog algoritma. Kod ovog križanja uzima se prvi grad iz jednog roditelja i
uspoređuju se gradovi u oba roditelja u koje se može doći iz izabranog grada.
Prilikom križanja nastaje jedan potomak u koji se kopira onaj slijed gradova
koji ima kraći put. Ako se grad već pojavio u djetetu tada se uzima neki drugi,
a ako je i taj već u djetetu tada se slučajno odabere neki još neodabrani grad.
GSX križanje
također se koristi kod rješavanja problema trgovačkog putnika. Kao kod
korištenja Pohlepnog križanja, slučajno se izabere jedan grad i u oba se
roditelja traži što je moguće dulji podskup gradova, koji su stazom povezani sa
izabranim gradom. Ako staza nije potpuna, tada se ostali gradovi dodaju
slučajnim redoslijedom. Ova vrsta križanja smatra se jednom od najefikasnijih u
rješavanju problema trgovačkog putnika jer se ovim križanjem najbolje čuva dobar
genetski materijal roditelja.
Mutacija je unarni
genetski operator koji se provodi za svaku jedinku generiranu operacijom
križanja, a rezultat mutacije je izmijenjena jedinka. Taj genetski operator
koristi se za dobivanje raznolikosti u populaciji i sprječava populaciju da
konvergira prema nekom lokalnom optimumu.
Vjerojatnost mutacije pm
je parametar koji određuje kolika je vjerojatnost da određeni gen neke jedinke
mutira. Taj broj mora biti u intervalu [0,1]. Ako vjerojatnost mutacije teži k
jedinici, tada će genetski algoritam slučajno pretraživati prostore rješenja.
Ukoliko vjerojatnost mutacije teži k nuli, tada postoji velika vjerojatnost da
će algoritam završiti u nekom od lokalnih optimuma.
Ako se ne koristi binarni
prikaz rješenja, tada vjerojatnost mutacije pojedinog gena nema smisla te se
definira vjerojatnost mutacije kromosoma pM koji se
računa formulom:
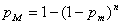 ,
gdje je n broj bitova u kromosomu.
,
gdje je n broj bitova u kromosomu.
Izbor vrste mutacije, koja će
se koristiti za rješavanja nekog problema, također ovisi o prikazu rješenja.
Kod binarnog
prikaza rješenja jednostavna mutacija djeluje tako da u slučajno odabranom
kromosomu invertira jedan slučajno odabrani bit.
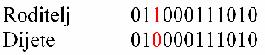
Slika 4‑ 6
Jednostavna mutacija (binarni prikaz rješenja)
Kako kod prikaza permutiranim
nizom ne smije doći do ponavljanja brojeva u nizu, ovakva mutacija nije pogodna.
Zbog toga jednostavna mutacija kod ovog prikaza slučajno izabere dva gena u
kromosomu i zamijeni njihova mjesta. Time se unosi raznolikost, a zadovoljen je
uvjet da se brojevi u nizu ne ponavljaju. Ova vrsta mutacije često se koristi
kod problema n-kraljica.
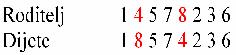
Slika 4‑7
Jednostavna mutacija (prikaz rješenja permutiranim nizom)
Miješajuća mutacija
slučajno odabere kromosom i dvije pozicije. Unutar te dvije pozicije izmiješaju
se ili invertiraju geni (invertirajuća miješajuća mutacija).
Potpuna miješajuća mutacija je
krajnji slučaj i kod nje se miješaju svi geni u kromosomu.
Pohlepna zamjenska
mutacija koristi se kod rješavanja problema trgovačkog putnika. Ova vrsta
mutacija jednaka je jednostavnoj mutaciji, no ima još jedan uvjet: do zamijene
gena u kromosomu dolazi samo ako je duljina staze u dobivenom kromosomu kraća od
duljine prije mutacije.
2opt metoda jedna
je od najpoznatijih metoda koji se koriste kod problema trgovačkog putnika. Ta
metoda odabire neku stazu unutar grafa i okreće poredak gradova u podstazi ako
se time dobiva kraća staza. Veliki problem 2opt metode je taj što može zapeti u
nekom lokalnom optimumu iz kojega, zbog načina usporedbe, više ne može izaći.
No, uz pravilno odabrane operatore križanja, koji će unijeti dovoljnu
raznolikost, ova mutacija postaje najefikasnija.
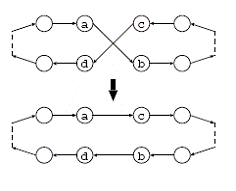
Slika 4‑8 2opt
mutacija
U početku su se
genetski algoritmi koristili većinom za rješavanje optimizacijskih problema, no
danas se oni koriste za rješavanje raznih klasa problema. Razlog tomu je to što
se genetski algoritmi mogu lako prilagoditi problemu. Ovi algoritmi našli su
svoju primjenu u organizaciji, kemiji, biologiji, neurologiji, tehnici itd…
Neke od problema u čijem se
rješavanju koriste genetski algoritmi su:
- automatizirani dizajn
- učenje kod neuronskih
mreža
- izračunavanje optimalnog
broja prijava mobilnih telefona baznim stanicama
- dijeljenje grafova
- problem raspoređivanja
procesa
- problem transporta
- razbijanje šifri
- dizajniranje sustava
opskrbe vodom
- učenje kretanja likova u
3D simuliranom svijetu
- dizajn univerzalnog motora
- sinteza CMOS operacijskih
pojačala
- itd…
Problem trgovačkog
putnika je problem kombinatrone optimizacije i pripada skupini NP-teških
problema. NP (ne-polinomijalni) problemi su problemi koje pomoću
determinističkih metoda nije moguće riješiti u polinomijalnom vremenu.. TSP je
jedan od problema koje je jednostavno formulirati, no nije jednostavno naći
kratki algoritam koji bi ga riješio.
Definicija tog problema je:
Zadana je mreža
gradova u kojoj su svaka dva grada međusobno povezana i zna se (najkraća)
udaljenost među njima. Trgovački putnik treba obići sve gradove i vratiti se
natrag u grad iz kojeg je krenuo tako da u svaki grad dođe samo jednom, a da pri
tome sveukupno prijeđe najkraću udaljenost.
Budući da je riječ o potpunom
grafu s n vrhova, ovaj problem ima 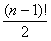 mogućih
rješenja. Zbog mogućeg broja rješenja potrebno je pronaći algoritam koji neće
provjeravati svako od rješenja već će nekom bržom metodom doći do onog
optimalnog. Zbog načina rada, genetski algoritmi su vrlo efikasni u rješavanju
ovog problema. Iako algoritam neće možda uvijek naći optimalno rješenje, raznim
pokusima je pokazano da se za čak 100 gradova skoro optimalno rješenje može
pronaći za manje od minutu. Kako je u praksi dovoljno pronaći rješenje koje je
blizu optimuma, ovaj algoritam je vrlo efikasan.
mogućih
rješenja. Zbog mogućeg broja rješenja potrebno je pronaći algoritam koji neće
provjeravati svako od rješenja već će nekom bržom metodom doći do onog
optimalnog. Zbog načina rada, genetski algoritmi su vrlo efikasni u rješavanju
ovog problema. Iako algoritam neće možda uvijek naći optimalno rješenje, raznim
pokusima je pokazano da se za čak 100 gradova skoro optimalno rješenje može
pronaći za manje od minutu. Kako je u praksi dovoljno pronaći rješenje koje je
blizu optimuma, ovaj algoritam je vrlo efikasan.
Već je spomenuto da se za prikaz
rješenja kod problem trgovačkog putnika najčešće koristi prikaz permutiranim
nizom u kojem brojevi u nizu označavaju redoslijed obilaska gradova.
Praktični dio ovog
rada je ispitivanje ponašanja genetskog algoritma u ovisnosti o parametrima koji
su mu zadani. U pokusima se promatralo vrijeme izvođenja algoritma i kvaliteta
rješenja (tj. duljina puta u rješenju). U programu koji se koristi u ovom
seminaru postoji mogućnost odabira prirodne i k-turnirske selekcije, GSX,
Pohlepnog i PMX križanja, te jednostavne, Pohlepne zamjenske i 2opt mutacije. U
svim pokusima uvjet završetka je 10 nepromijenjenih najboljih, ε je 0.00005, a
veličina turnira je 3. Podaci koji su prikazani u tablicama dobiveni su kao
prosječne vrijednosti 5 mjerenja.
Problem nad kojim su se vršili
pokusi je berlin52, jedan od standardnih problema za testiranje algoritama koji
rješavaju problem trgovačkog putnika.
Bitno je naglasiti da su podaci
dobiveni u ovim pokusima samo okvirni zbog načina rada genetskih algoritama.
U prvom pokusu
proučavao se rad genetskog algoritma u ovisnosti o veličini populacije. Veličina
populacije u nepravilnim razmacima mijenjala od 10 do 10000. Vjerojatnost
eliminacije je tijekom cijelog pokusa iznosila 30%, a vjerojatnost mutacije 10%.
Rezultati pokusa prikazani su u
Tablica 5.1, te na
Slika 5‑1
i Slika 5‑2.
Tablica 5. 1 Ovisnost kvalitete rješenja i vremena
izvođenja o veličini populacije
|
Veličina populacije |
najbolje rješenje |
prosječno rješenje |
prosječno vrijeme izvođenja (s) |
|
10 |
239801,44 |
254814,46 |
1,14 |
|
50 |
217938,25 |
179712,17 |
1,75 |
|
100 |
222468,32 |
230740,01 |
1,41 |
|
200 |
227380,54 |
234860,37 |
1,71 |
|
500 |
212598,91 |
231333,69 |
3,69 |
|
1000 |
200130,73 |
220283,60 |
6,58 |
|
2000 |
212927,91 |
219678,38 |
15,47 |
|
5000 |
194448,45 |
208877,36 |
44,59 |
|
10000 |
195129,74 |
203468,41 |
125,44 |

Slika 5‑1 Ovisnost vremena izvođenja o veličini
populacije

Slika 5‑2 Ovisnost kvalitete rješenja o veličini
populacije

Slika 5‑3
Primjer jednog izvođenja algoritma s veličinom populacije od 50 jedinki
U ovom pokusu može se vidjeti da
se vrijeme izvođenja povećava s veličinom populacije, a duljina puta se
smanjuje. Povećanjem broja jedinki u populaciji veća je raznolikost pa je i veća
vjerojatnost da će se više dobrih gena prenijeti na potomke. Velika iznimka je
za populaciju veličine 50 no to je vjerojatno zbog slučajno dobivenih dobrih
rješenja. Ako uzmemo u obzir vrijeme izvođenja i duljinu puta, vidimo da su
najbolji slučajevi oko populacije veličine 100, pa tu veličinu koristimo u
daljnjim pokusima.
Nakon što se
odredila optimalna veličina populacije, promatra se utjecaj vjerojatnosti
eliminacije na rješenje i vrijeme izvođenja. Prirodna eliminacijska selekcija
odvija se tako da se iz početne populacije eliminira
 jedinki.
Kako se kod vjerojatnosti eliminacije blizu 100% algoritam blokirao jer je
gotovo cijela populacija bila eliminirana, pokus se provodio za vrijednosti
vjerojatnosti eliminacije od 0 do 95%. Vjerojatnost mutacije iznosila je 10%.
jedinki.
Kako se kod vjerojatnosti eliminacije blizu 100% algoritam blokirao jer je
gotovo cijela populacija bila eliminirana, pokus se provodio za vrijednosti
vjerojatnosti eliminacije od 0 do 95%. Vjerojatnost mutacije iznosila je 10%.
Rezultati pokusa dani su u
Tablica 5.3 te na
Slika 5‑4
i
Slika 5‑5.
Tablica 5.2 Ovisnost vremena izvođenja i kvalitete rješenja o vjerojatnosti
križanja
|
veličina populacije |
najbolje rješenje |
prosječno rješenje |
prosječno vrijeme izvođenja (s) |
|
0,00 |
245127,00 |
252633,46 |
0,34 |
|
10,00 |
244182,21 |
249375,28 |
0,67 |
|
20,00 |
221509,75 |
237318,48 |
0,87 |
|
30,00 |
217046,84 |
232122,00 |
1,48 |
|
40,00 |
209702,43 |
222108,43 |
1,72 |
|
50,00 |
159911,09 |
209910,95 |
3,02 |
|
55,00 |
116435,69 |
182937,48 |
6,15 |
|
60,00 |
124629,41 |
169236,64 |
9,68 |
|
70,00 |
114261,56 |
147381,24 |
12,45 |
|
80,00 |
109173,94 |
138615,15 |
13,41 |
|
90,00 |
115075,88 |
127770,25 |
17,21 |
|
95,00 |
14515,58 |
141054,01 |
10,15 |

Slika 5‑4 Ovisnost vremena izvođenja o vjerojatnosti
eliminacije

Slika 5‑5 Ovisnost kvalitete rješenja o
vjerojatnosti eliminacije

Slika 5‑6 Primjer
jednog izvođenja algoritma uz vjerojatnost eliminacije 90%
Proučavanjem rezultata ovih
pokusa dolazi se do zaključka kako vrijeme izvođenja raste s vjerojatnošću
mutacije sve do 90%, a nakon toga počinje opadati (zbor već navedenog razloga).
Duljina puta u rješenju opada s porastom vjerojatnosti mutacije do 90%, a nakon
toga počinje rasti. U pokusu je dobivena velika razlika u rješenju i vremenu
izvođenja kod vjerojatnosti od 50% i 60% pa je zato napravljen još jedan pokus s
vjerojatnosti 55%, koja se pokazala kao optimalna.
U trećem pokusu
promatraju se vrijeme izvođenja i kvaliteta rješenja za različite vrijednosti
vjerojatnosti mutacije. Veličina populacije je 100, vjerojatnost eliminacije
55%, a vjerojatnost mutacije mijenja se od 0 do 100%. Rezultati pokusa prikazani
su u Tablica 5.3 te na
Slika 5‑7
i Slika 5‑8.
Tablica 5. 3 Ovisnost vremena izvođenja i kvalitete
rješenja o vjerojatnosti mutacije
|
vjerojatnost mutacije |
najbolje rješenje |
prosječno rješenje |
prosječno vrijeme izvođenja (s) |
|
0,00 |
180589,24 |
207648,57 |
3,40 |
|
10,00 |
139905,57 |
149527,74 |
5,92 |
|
20,00 |
195662,59 |
216441,98 |
2,05 |
|
30,00 |
113162,81 |
168804,71 |
9,63 |
|
40,00 |
112976,25 |
188115,60 |
6,14 |
|
50,00 |
177597,51 |
206447,69 |
3,19 |
|
60,00 |
135382,67 |
196698,11 |
5,01 |
|
70,00 |
128652,13 |
192541,86 |
6,00 |
|
80,00 |
168697,35 |
188452,17 |
4,92 |
|
90,00 |
183645,46 |
214276,67 |
2,71 |
|
100,00 |
124937,51 |
195994,27 |
6,33 |

Slika 5‑7 Ovisnost vremena izvođenja o vjerojatnosti
mutacije

Slika 5‑8 Ovisnost kvalitete rješenja o
vjerojatnosti mutacije
Iako se u prva dva pokusa
uočavala pravilnost između parametra koji su se mijenjali i onih koji su se
mjerili, u ovom pokusu to nije slučaj. Kada vjerojatnost mutacije teži k 0,
algoritam brzo konvergira k nekom lokalnom optimumu. Suprotno tome, kada
vjerojatnost teži k 100% algoritam se bazira na slučajnom odabiru. Niti jedan od
ova dva slučaja nije dobar, što se vidi i iz grafova. Uzimajući u obzir
kompromis između vremena izvođenja i duljine puta, vjerojatnost od 40% uzima se
kao najbolja.
Kako program, koji
se koristi za pokuse u ovom seminaru, nudi mogućnost odabira između više vrsta
selekcije, križanja i mutacije, zanimljivo je pronaći optimalnu kombinaciju za
rješavanje ovog problema. U pokusu je zadržana veličina populacije od 100
jedinki, vjerojatnost eliminacije 55% i vjerojatnost mutacije 40%. Rezultati za
svaku kombinaciji dani su u Tablica 5.4, a
kombinacije se lako mogu usporediti na Slika 5‑9
i Slika 5‑10.
Tablica
5. 4 Usporedba kombinacija selekcije, križanja i mutacije
|
kombinacija |
najbolje rješenje |
prosječno rješenje |
vrijeme izvođenja (s) |
|
prirodna selekcija + GSX + jednostavna mutacija |
166721,60 |
190849,79 |
4,22 |
|
prirodna selekcija + GSX + Greedy swap mutacija |
145273,31 |
191291,44 |
4,46 |
|
prirodna selekcija + GSX + 2opt mutacija |
75443,66 |
75443,66 |
4,15 |
|
prirodna selekcija + Greedy crossover + jednostavna
mutacija |
86621,30 |
90293,01 |
8,25 |
|
prirodna selekcija + Greedy crossover + Greedy swap
mutacija |
90998,47 |
95294,61 |
4,60 |
|
prirodna selekcija + Greedy crossover + 2opt mutacija |
75443,66 |
75443,66 |
2,96 |
|
prirodna selekcija + PMX + jednostavna mutacija |
211103,44 |
218644,11 |
4,44 |
|
prirodna selekcija + PMX+ Greedy swap mutacija |
175043,26 |
206713,18 |
4,27 |
|
prirodna selekcija + PMX + 2opt mutacija |
78213,05 |
78835,44 |
1,71 |
|
turnirska selekcija + GSX + jednostavna mutacija |
110073,14 |
193666,57 |
59,51 |
|
turnirska selekcija + GSX + Greedy swap mutacija |
112287,12 |
194281,97 |
60,15 |
|
turnirska selekcija + GSX + 2opt mutacija |
75443,66 |
75443,66 |
21,17 |
|
turnirska selekcija + Greedy crossover + jednostavna
mutacija |
86907,64 |
96080,23 |
35,62 |
|
turnirska selekcija + Greedy crossover + Greedy swap
mutacija |
102379,99 |
103120,83 |
37,39 |
|
turnirska selekcija + Greedy crossover + 2opt mutacija |
75443,66 |
75443,66 |
15,36 |
|
turnirska selekcija + PMX + jednostavna mutacija |
11516,53 |
95147,55 |
141,09 |
|
turnirska selekcija + PMX+ Greedy swap mutacija |
116396,56 |
124752,21 |
137,64 |
|
turnirska selekcija + PMX + 2opt mutacija |
75443,66 |
75443,66 |
9,39 |

Slika 5‑9 Usporedba vremena
izvođenja za razne kombinacije selekcije, križanja i mutacije

Slika 5‑10 Usporedba
kvalitete rješenja za razne kombinacije selekcije, križanja i mutacije
Uspoređujući podatke dobivene u ovom pokusu lako se može zaključiti da je
najbolja kombinacija:
prirodna selekcija + Greedy crossover + 2opt
mutacija.
Već
spomenuta efikasnost 2opt mutacije mogla se primijetiti tijekom pokusa jer
je kod korištenja te mutacije algoritam gotovo uvijek došao do optimalnog
rješenja, dok se za druge vrste mutacije duljine puta bitno razlikuju od
optimalne. Može se također vidjeti da ova vrsta mutacije zahtjeva najmanje
vremena.
Na
Slika 5‑11 i
može se vidjeti usporedba GSX i PMX mutacije. Kod korištenja GSX mutacije
algoritam je došao do optimalnog rješenja (75443,66), a sa PMX prosječno
rješenje je bilo malo veće (78835,44).


Slika
5‑11 prirodna selekcija+ GSX +2 opt i prirodna selekcija +
PMX + 2opt
Ako
uspoređujemo optimalno rješenje problema Berlin52 ovim algoritmom i
trenutačno optimalno rješenje dostupno na [12],
vidimo da se oni puno ne razlikuju. To pokazuje da je ovaj algoritam
efikasan za rješavanje tog i sličnih problema.
Problem N-kraljica također pripada skupini NP problema.
Definicija problema je:
Na ploči veličine
 treba
postaviti n kraljica tako da se one međusobno ne napadaju. Dvije kraljice se
napadaju ako su u istom retku, istom stupcu ili na istoj dijagonali.
treba
postaviti n kraljica tako da se one međusobno ne napadaju. Dvije kraljice se
napadaju ako su u istom retku, istom stupcu ili na istoj dijagonali.
Za
prikaz rješenja kod rješavanja ovog problema najčešće se koristi prikaz
permutiranim nizom gdje indeks u nizu označava stupac, a broj u nizu
označava redak u kojima se nalazi kraljica (može i obrnuto). Već je,
korištenjem ovog prikaza, zadovoljen uvjet da se dvije kraljice ne smiju
naći u istom retku ili istom stupcu, te se samim time smanjuje složenost
problema sa  na
na
 .
No, to je još uvijek velika složenost, pa se zato koriste genetski
algoritmi.
.
No, to je još uvijek velika složenost, pa se zato koriste genetski
algoritmi.
Nakon
odabira prikaza rješenja potrebno je definirati funkciju dobrote. To je kod
ovog problema dosta teško zato što je dobiveno rješenje ili točno ili
pogrešno. Funkcija dobrote treba određivati koliko je neko rješenje
pogrešno. Kako je, zbog načina prikaza, rješenje pogrešno samo ako se
kraljice nalaze na istim dijagonalama, funkcija dobrote najčešće broji te
konflikte na dijagonalama. Što je broj konflikata veći, to je rješenje
lošije.
Za pokuse, u kojima se proučavao utjecaj parametara na broj
generacija koje su bile potrebne algoritmu da dođe do rješenja, koristila se
aplikacija dostupna na [11].
Autor
tog algoritma koristio je prikaz rješenja permutiranim nizom gdje je indeks
označavao redak, a broj u nizu stupac u kojima se nalazi pojedina kraljica.
Vrsta križanja koja se koristila bila je PMX križanje, a mutacija je bila
jednostavna.
U
pokusu se proučavala ovisnost broja generacija o veličini populacije,
vjerojatnosti križanja i vjerojatnosti mutacije za 10 i 100 kraljica. Pokusi
s problemom 100 kraljica provedeni su je jer je broj generacija kod problema
10 kraljica jako varirao. Prosječan broj generacija dobiven je kao srednja
vrijednost izvođenja 10 pokusa.
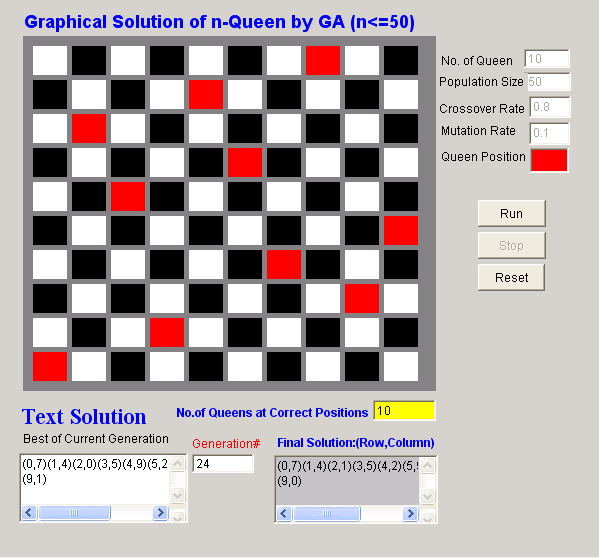
Slika 5‑12 Primjer rješenja za problem 10 kraljica
U prvom pokusu proučavala se ovisnost broja generacija o
veličini populacije. Vjerojatnost križanja bila je 80%, vjerojatnost
mutacije 10%, a veličina populacije mijenjala se od 50 do 10000 jedinki za
problem 10 kraljica i od 150 do 10000 jedinki za problem 100 kraljica.
a)
10 kraljica
Tablica 5.5 Prosječan br. generacija
|
veličina
populacije |
pros. br.
generacija |
|
50 |
18,8 |
|
100 |
13,5 |
|
200 |
8,4 |
|
500 |
4,3 |
|
1000 |
3,3 |
|
2000 |
1,4 |
|
5000 |
0,3 |
|
10000 |
0,2 |

Slika 5‑13 Ovisnost broja generacija o veličini
populacije kod problema 10 kraljica
b) 100
kraljica
Tablica 5. 6 Prosječan br. generacija
|
veličina
populacije |
pros. br.
generacija |
|
150 |
240,5 |
|
200 |
175,9 |
|
500 |
170,2 |
|
1000 |
186,4 |
|
2000 |
166,7 |
|
5000 |
79,4 |
|
10000 |
49,5 |

Slika 5‑14 Ovisnost broja generacija o veličini
populacije kod problema 100 kraljica
Kao što
se vidi iz tablica i grafova, broj generacija opada s povećanjem veličine
populacije. Kod problema 10 kraljica može se uočiti da algoritam s
populacijom većom od 5000 vrlo često pronađe rješenje u nultoj generaciji,
tj. u populaciji postoji kromosom s rješenjem već prilikom inicijalizacije.
Kada se
u obzir uzme i brzina izvođenja, optimalna veličina populacije za 10
kraljica je 500, a za 100 kraljica 2000 jedinki, pa se te vrijednosti
koriste u daljnjim pokusima.
U slijedećem koraku promatra se utjecaj vjerojatnosti križanja
na broj generacija. Kao veličine populacija iskorišteni su podaci dobiveni u
prošlom pokusu, a vjerojatnost mutacije je 10%.
a)
10 kraljica
Tablica 5.7 Prosječan br. generacija
|
vjerojatnost
križanja |
pros. br.
generacija |
|
0,00 |
5,2 |
|
10,00 |
4,8 |
|
20,00 |
6,7 |
|
30,00 |
4,3 |
|
40,00 |
2,7 |
|
50,00 |
5,9 |
|
60,00 |
7,5 |
|
70,00 |
5 |
|
80,00 |
4,8 |
|
90,00 |
5,1 |
|
100,00 |
6 |

Slika 5‑15 Ovisnost broja generacija o vjerojatnosti
križanja kod problema 10 kraljica
b)
100 kraljica
Tablica 5.8 Prosječan br. generacija
|
vjerojatnost
križanja |
pros. br.
generacija |
|
0,00 |
185,7 |
|
10,00 |
158 |
|
20,00 |
162 |
|
30,00 |
157,9 |
|
40,00 |
148,3 |
|
50,00 |
141 |
|
0,00 |
143,5 |
|
70,00 |
144,9 |
|
80,00 |
145,9 |
|
90,00 |
184,7 |
|
100,00 |
277,9 |

Slika 5‑16 Ovisnost broja generacija o vjerojatnosti
križanja kod problema 100 kraljica
Iako se
kod problema 10 kraljica čini da broj generacija ne ovisi pravilno o
vjerojatnosti križanja, kod problema 100 kraljica pokazano je da nije tako.
Broj generacija je velik za vjerojatnosti 0% i 100%, a najmanji je za
srednje vrijednosti vjerojatnosti križanja. Za optimalnu vrijednost ovog
parametra uzeto je 40% kod problema 10 kraljica i 50% kod problema 100
kraljica te se te vrijednosti koriste u slijedećem pokusu.
U zadnjem pokusu promatra se utjecaj vjerojatnosti mutacije na
broj generacija uz vrijednosti parametara određene prethodnim pokusima.
a)
10 kraljica
Tablica 5.9 Prosječan br. generacija
|
vjerojatnost
mutacije |
pros.br.
generacija |
|
0,00 |
3,7 |
|
10,00 |
4,1 |
|
20,00 |
6,6 |
|
30,00 |
5,1 |
|
40,00 |
6,1 |
|
50,00 |
5 |
|
60,00 |
4 |
|
70,00 |
4,4 |
|
80,00 |
5,3 |
|
90,00 |
4,4 |
|
100,00 |
6 |

Slika
5‑17 Ovisnost broja generacija o vjerojatnosti mutacije kod problema 10
kraljica
b)
100 kraljica
Tablica 5.10 Prosječan br. generacija
|
vjerojatnost
mutacije |
pros. br.
generacija |
|
0,00 |
147,4 |
|
10,00 |
135,3 |
|
20,00 |
144,3 |
|
30,00 |
139,8 |
|
40,00 |
152,1 |
|
50,00 |
152,2 |
|
60,00 |
157,9 |
|
70,00 |
144 |
|
80,00 |
144,1 |
|
90,00 |
143,4 |
|
100,00 |
164,4 |

Slika
5‑18 Ovisnost broja generacija o vjerojatnosti mutacije kod problema 100
kraljica
U ovom
pokusu vidimo da za oba problema broj generacija ne ovisi pravilno o
vjerojatnosti mutacije. Kod oba problema vrijednost ovog parametra kod koje
se dobiju najbolji rezultati je 10%.
U New Mexicu na jednom sveučilištu pokrenut je projekt primjene
genetskih algoritama za portretiranje osumnjičenika kako bi se zamijenili
klasični fotoroboti. U sustavu se nalaze različite crte lica (usta, kosa,
oči, nos i brada) koji se algoritmom kombiniraju i 20 lica se izbacuje na
ekran. Svjedok tada ocjenjuje sličnost svakog od tih lica sa osumnjičenikom
(na skali od 1 do 10). Genetski algoritam tada, na temelju tih ocjena (koje
koristi kao dobrotu), generira novu generaciju osumnjičenika. Algoritam se
zaustavlja kada svjedok nađe lice dovoljno slično osumnjičeniku. U
provedenom testu svjedoci su vidjeli simuliranu kriminalnu radnju, a
osumnjičenik je pronađen za 3 dana.
U Finskoj su dva inženjera pokušala napisati genetski algoritam
koji bi rješavao sudoku. Za prikaz rješenja koristili su polje od 81 broj,
podijeljeno na 9 podnizova. U svakom od podnizova nije se smio ponavljati
neki broj. Operacija križanja definirana je tako da mijenja cijeli podniz u
nizu, a mutacija je mijenjala brojeve samo unutar podniza. Za definiranje
funkcije dobrote koristila su se dva pravila: zbroj brojeva u svakom retku i
stupcu mora biti 45, a produkt 9!.
Za
provođenje testova na ovom algoritmu uzeto je 5 sudoku-a različitih težina
(1-5 zvjezdica) iz novina Helsingin Sanomat(2006) i 4 sudokua različitih
težina iz novina Aamulehti(2006). Također su testirali generiranje novog
sudokua.
Ipak,
rezultati eksperimenata nisu bili obećavajući. Teže probleme algoritam je
uspio riješiti u samo par posto slučajeva. No, ovi testovi ipak nisu bili
uzaludni. Otkriveno je kako se genetski algoritmi mogu koristiti u
ocjenjivanju težine pojedinog sudoku-a. Isto tako, ovi se algoritmi mogu
koristiti u stvaranju novih sudoku zadataka. Algoritam generira rješenje i
tada miče broj po broj sve dok je moguće naći jedinstveno rješenje.
Iako ljudi genetske algoritme koriste napisane i pokrenute na
kompjuteru, postoji slučaj kada i njihov mozak koristi princip rada tih
algoritama, a da toga nisu ni svjesni.
Kod
igranja igre Mastermind igrač najprije odabire 4 boje, ovisno o broju boja
koje je pogodio (što igra ulogu dobrote), igrač koristi odabrane boje i
križa ih s onima iz prethodnog koraka. Ako, nakon par koraka, nije pronašao
rješenje, igrač mijenja jednu ili više boja (mutacija). Uvjeti zaustavljanja
kod igre su pronalazak rješenja ili određen broj koraka (broj mogućih rupica
za popunjavanje na ploči za igranje).
Kroz opis rada genetskog algoritama te izvođenjem pokusa s parametrima,
moglo se vidjeti kako su genetski algoritmi vrlo snažna metoda optimiranja.
Na primjeru trgovačkog putnika i n-kraljica može se vidjeti kako su genetski
algoritmi vrlo korisni za rješavanje onih klasa problema koje se klasičnim
metodama ne mogu riješiti ili njihovo izvođenje dugo traje.
Praktični rad je pokazao da odabir parametara genetskih algoritama znatno
utječe na brzinu i kvalitetu rješenja. Zbog toga je vrlo važno odabrati
optimalnu kombinaciju parametara. Jedan od nedostataka genetskih algoritama
je u tome što ne postoji sustavan postupak za određivanje dobrih parametara
pa se traženje ispravne kombinacije svodi na eksperimentiranje.
U
pokusima se može uočiti kako se vrijeme izvođenja i broj generacija povećava
s povećanjem broja jedinki u populaciji, a duljina puta se smanjuje. Zbog
toga treba pronaći kompromis između kvalitete rješenja i brzine izvođenja.
Iako je
brzina izvođenja, u usporedbi s ostalim metodama optimiranja, relativno
mala, genetski algoritmi našli su svoju primjenu u raznim područjima
ljudskog rada. Danas se sve više proučavaju paralelni genetski algoritmi jer
se njihovim korištenjem znatno povećava brzina rada.
[1]
Marin Golub., doc.dr.sc, "Genetski algoritam" -
http://www.zemris.fer.hr/~golub/ga/ga_skripta1.pdf
[2] Marin
Golub, doc.dr.sc, "Genetski algoritam" -
http://www.zemris.fer.hr/~golub/ga/ga_skripta2.pdf
[3] Marko
Božiković, "Globalni paralelni genetski algoritmi" -
http://www.zemris.fer.hr/~golub/ga/studenti/bozikovic_gpga.pdf
[4] Vedran
Lovrečić, "Genetski algoritmi u primjeni" -
http://www.zemris.fer.hr/~golub/ga/studenti/lovrecic/Genetski%20algoritam%20u%20primjeni.htm
[5] Timo
Mantere and Jane Koljonen, "Solving and Rating Sudoku Puzzles with Genetic
Algorithms",
http://www.stes.fi/scai2006/proceedings/step2006-86-mantere-solving-and-rating-sudoku-puzzles.pdf
[6]
"Genetic algorithm",
http://en.wikipedia.org/wiki/Genetic_algorithm
[7]
Vinko Bradvica, "Algoritmi koji oponašaju procese u prirodi",
http://www.zemris.fer.hr/~golub/ga/studenti/seminari/2007_bradvica/index.html
[8]
prof. dr. Vlatko Čerić, "Genetski algoritmi",
http://web.efzg.hr/dok/INF/Ceric/spo/(2d)_genetski_algoritmi.pdf
[9] "Genethic
algortihms ",
http://www.obitko.com/tutorials/genetic-algorithms/
[10] "Solving
n-Queen problem using global paralell genetic algorithm",
http://www.zemris.fer.hr/~golub/clanci/eurocon2003.pdf
[11] "Solution
of n-Queen Problem by Genetic Algorithm",
http://www.iba.k.u-tokyo.ac.jp/english/userlog.cgi?queenrun
[12] "Optimal
solutions for symmetric TSPs",
http://www.informatik.uni-heidelberg.de/groups/comopt/software/TSPLIB95/STSP.html
Tema ovog rada su genetski algoritmi. Opisuje se kakvi su to
točno algoritmi i kako rade. Kod takvih algoritama problemi se rješavaju
evolucijskim procesom koji rezultira najboljim rješenjem. Naglasak je
stavljen na načine prikaza ili predstavljanja rješenja, genetske operatore
(selekcija, križanje i mutacija) te parametre (vjerojatnosti križanja i
mutacije i veličina populacije). U drugom dijelu rada opisana je primjena
genetskih algoritama. Detaljnije se opisuju problemi trgovačkog putnika i N
kraljica koji pripadaju skupini NP-problema za čije se rješavanje genetski
algoritmi često koriste.