|
Funkcijama raspršenog skupa točaka mogu se opisati
glatke 2D konture ili 3D površine.
Postupak definiranja objekata u 2D prostoru:
 |
 |
 |
|
Zadaju se rubne točke (crveno na slici).
Svim rubnim točkama se pridijeli vrijednost 0. Ova vrijednost
označava da kroz te točke prolazi kontura koju opisujemo.
Svaka rubna točka ima pripadnu
točku normale (označene žuto). Točkama normale se pridjeljuje
mala pozitivna vrijednost i smješta ih se od rubne točke prema
unutrašnjosti krivulje.
Time je određen raspršeni
skup točaka. Potrebno je odrediti takvu funkciju f(x)
koja će u svim rubnim točkama poprimati vrijednost 0,
a u svim točkama normale malu pozitivnu vrijednost. Funkcija
mora za bilo koju vrijednost unutar krivulje davati pozitivnu
vrijednost, a izvan krivulje negativnu.
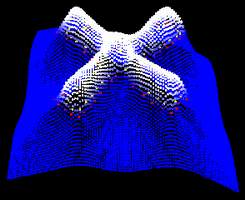
Na drugoj slici vidi se
funkcija raspršenog skupa točaka f(x), za objekt sa
prve slike. Funkcija je prikazana u 3D prostoru, tako da je
za treću koordinatu uzeta vrijednost točke. Bijelom bojom
su označene točke sa pozitivnom vrijednošću. Vrijednosti točaka
unutar krivulje variraju, što je vidljivo iz pojedinih blagih
izbočenja na krajevima i u središtu objekta X. Vidljivo je
kako funkcija nema oštrih vrhova, što će se pokazati kao odlično
svojstvo za preobražaj objekata.
Treća slika prikazuje objekt
kada se odaberu samo točke koje se nalaze unutar krivulje.
|
Postavlja se pitanje kako konstruirati prethodno
opisanu implicitnu funkciju f(x). Za konstruiranje funkcije
f(x) koristi se metoda interpolacije raspršenog skupa točaka
(engl. scattered data interpolation) koristeći radij-funkcije.
Jednadžba funkcije f(x):
|
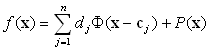 (1) (1)
cj - zadane točke
(rubne točke i točke normale)
dj - težinski koeficijenti
P(x) - polinom prvog stupnja kojim se opisuje
konstantni linearni pomak čitave površine
x - točka za koju se traži vrijednost funkcije
|
|
Odabir radij funkcije ovisi o prostoru
u kojem se radi:
za 2D, 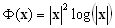
za 3D, 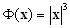
|
|
Budući da smo zadali rubne točke i točke
normale, vrijedi
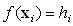 , gdje je h vrijednost pojedine točke. (2)
, gdje je h vrijednost pojedine točke. (2)
Još je samo potrebno odrediti
težinske koeficijente dj i koeficijente polinoma P.
Koristeći jednadžbu (1) i (2), postavlja se sustav n
jednadžbi sa n nepoznanica u obliku:
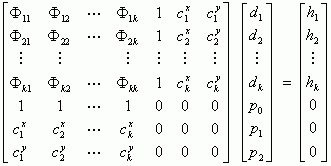 (3) (3)
Za rješavanje sustava može
se koristiti npr. metoda Gaussove eliminacije ili metoda LU
dekompozicije. Kada se dobiju nepoznanice, odnosno težinski
koeficijenti dj i koeficijenti polinoma P, koristeći
ove koeficijente, definirane rubne točke i točke normale,
prema jednadžbi (1), moguće je odrediti vrijednost bilo koje
točke u prostoru, što znači da smo dobili traženu funkciju
f(x).
|
Postupak definiranja objekata u 3D prostoru:
Objekti se u 3D prostoru određuju
na potpuno isti način kao i u 2D prostoru, samo što se u sustav
dodaje još jedna prostorna koordinata. Ručno unošenje rubnih točaka
i točaka normale ne bi bilo praktično u 3D prostoru. Zbog toga se
mogu koristiti objekti zapisani u 3D datotekama (npr. 3ds, ply,
obj itd...).
|



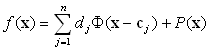 (1)
(1)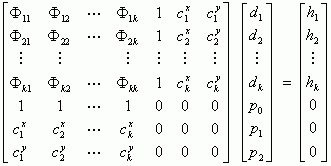 (3)
(3)