Fizikalni model

Čestice

Jedan od osnovnih elemenata od kojih se gradi model tkanine su čestice (eng. particle). Čestica je definirana kao točka u prostoru koja ima određena svojstva, a sama ne može predstavljati geometrijsku površinu. U ovom modelu čestice će posjedovati svojstvo mase i nad njima će se simulirati osnovni zakoni dinamike.

Opruga

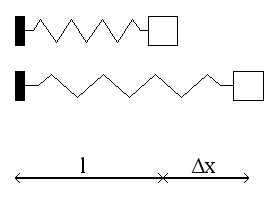
Slika 1. Opruga

U fizici, Hookov zakon elastičnosti je aproksimacija koja tvrdi da ako neku oprugu rastegnemo za udaljenost  od njenog položaja mirovanja, rezultirajuća sila , koju stvara opruga, je proporcionalna udaljenosti  i konstanti opruge , a njen smjer je suprotan od smjera pomaka:

Opruga koja zadovoljava ovu jednakost se naziva linearna opruga, a materijali za koje ona vrijedi se nazivaju linearno elastični materijali.

Ako se opruga koja zadovoljava jednadžbu (1) pokrene u titranje, ona će oscilirati beskonačno dugo, jer nema gubitka energije u sustavu. Da bi se riješio taj problem uvodi se i faktor prigušenja opruge . Sila prigušenja se računa jednostavnom linearnom jednadžbom:

gdje je:

•  -sila prigušenja
•  -koeficijent prigušenja opruge
•  -brzina promjene položaja opruge

Zbrajanjem jednadžbi (1) i (2) dobije se jednadžba koja predstavlja silu opruge:

Model tkanine

Model tkanine je mreža koja se sastoji od  čestica koji predstavljaju virtualnu masu tkanine. Svaka čestica je povezana sa susjednim česticama simuliranim oprugama koji nemaju masu i čija nazivna dužina je veća od nule. Spoj između čestica je realiziran na tri načina:

• strukturne opruge (eng. structural springs) – opruge koje povezuju čestica  i , te čestica  i
• smične opruge (eng. shear springs) – opruge koje povezuju čestica  i , te čestica  i
• pregibne opruge (eng. bend springs) – opruge koje povezuju čestica  i , te čestica  i

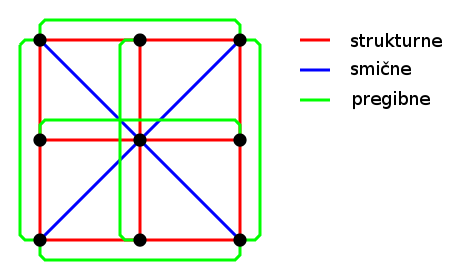
Slika 2. Dio mreže modela tkanine

Nazivi grupa opruga proizlaze iz njihove namjene u fizikalnom prikazu modela. Pod djelovanjem smičnog opterećenja djeluju samo smične opruge, pod djelovanjem pregibnog opterećenja djeluje samo pregibne opruge, dok pod djelovanjem sažimanja ili rastezana djeluju strukturne opruge.

Sile

Uz činjenicu da se simulira na mreži čestica dimenzija , može se pozicija svake od njih u ovisnosti o vremenu prikazati kao , gdje je  i . Promjena stanja modela se vode prema drugom Newtonovom zakonu:

Gdje je  masa,  ubrzanje, a  sila čestice  mreže modela.

Sila koja djeluje na pojedinu točku () je kombinacija unutarnjih sila modela, te vanjskih sila koje djeluju na model.

Unutarnje sile modela

Unutarnja sila modela je sila kojom opruge djeluju na točke mase koje se nalaze na njenim krajevima. Ona je definirana sumom Hookovog zakona (1) i jednadžbe titranja opruge (2).

gdje je:

•  - rezultirajuća sila kojom opruge djeluju na česticu 
• - skup koji sačinjavaju svi parovi , takvi da su čestice  oprugom povezane s česticom
• - vektor između dviju čestice  povezane oprugom
• - nazivna dužina opruge koja povezuje čestice  i
• - koeficijent opruge koja povezuje čestice  i
• - koeficijent prigušenja opruge koja povezuje čestice  i
•  - skalarna projekcija vektora brzine čestice  na vektor
•  - skalarna projekcija vektora brzine čestice  na vektor

U jednadžbi (5) prva suma predstavlja sumu svih sila koje nastaju djelovanjem opruge, pomaknute iz ravnotežnog položaja, spojene između dvije čestice, dok druga suma predstavlja silu prigušenja nastala promjene dužina opruga.

Vanjske sile modela

U vanjske sile ulaze sile gravitacije i sile koje prouzrokuje protok fluida konstantne brzine (npr. vjetra).

Sila gravitacije na svaku česticu  iznosi:

gdje je:

• - masa čestice
• - vektor smjera i snage djelovanja gravitacijskog ubrzanja

Sila koju stvara protok fluida na česticu  iznosi:

gdje je:

• - normala na površinu u čestici  mreže modela
• - vektor smjera i brzine protoka fluida
• - vektor brzine čestice

Simulacija modela

Primjenom gore navedenih jednadžbi moguće je izračunati vektor ukupne sile koja djeluje na pojedinu česticu  u nekom trenutku:

Pošto je za svaku česticu poznata njena masa, iz vektora sile se može primjenom drugog Newtonovog zakona (4) izračunati vektor ubrzanja pojedine čestice:

 
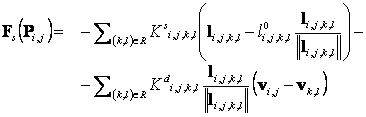
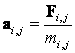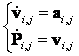Kako je akceleracija definirana kao promjena brzine po vremenu, njenom integracijom po vremenu se dobije brzina, dok se integracijom brzine dobiva pozicijom. Poveznica između pozicije čestice  i njenog ubrzanja  se nađe razrješenjem slijedećih diferencijalnih jednadžbi: