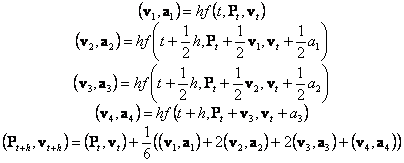Programska implementacija

Izvedba aplikacije

Aplikacija je pisana u C++ programskom jeziku korištenjem Microsoft Visual Studio 2005 razvojnog sučelja. Za iscrtavanje simulacijskog dijela je korištena OpenGL biblioteka, dok je za razvoj korisničkog sučelja korištena wxWidgets biblioteka (http://www.wxwidgets.org). wxWidgets je besplatna datoteka pisana u C++ razvojnom jeziku, a karakteriziraju je otvorenost izvornog koda i više-platformska podrška. Za učitavanje ulaznih datoteka u XML obliku korištena je libXml2 biblioteka (http://xmlsoft.org), dok su za učitavanje 3D modela zapisanih u 3DS datotečnom obliku, te učitavanje slika zapisanih u nekoliko oblika korištene biblioteke lib3DS (http://lib3ds.sourceforge.net), te DevIL (http://openil.sourceforge.net). Za potrebe otkrivanja kolizije korištena je SOLID biblioteka (http://www.dtecta.com).

Simulacijski model

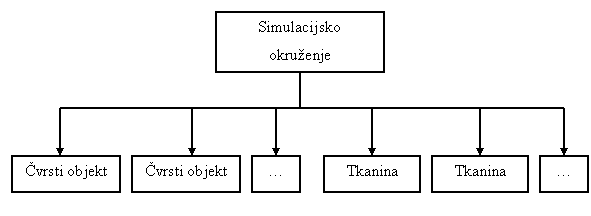
Slika 6. Model implementacije simulacijskog okruženja

Geometrijski objekti

Prilikom programske implementacije geometrijskih objekata ostvareno je virtualno sučelje Entity koje sadrži podatke zajedničke svim tipovima geometrijskih objekata. Podatci zajednički svim objektima su naziv geometrijskog objekta, te matrica transformacije. Naziv objekta je niz znakova koji korisniku omogućuje jednostavnije razlikovanje objekata u sceni, dok je matrica transformacije matrica brojeva s pomičnim zarezom jednostruke preciznosti dimenzija 4x4 kojom se definira položaj i orijentaciju pojedinog geometrijskog objekta unutar okruženja. Matrica transformacije je zapisana kao jednodimenzionalno polje od 16 brojeva jednostruke preciznosti u OpenGL obliku zapisa.

U programskoj implementaciji su definirana dva različita tipa geometrijskih objekata. To su geometrijski objekt tkanine i čvrsti geometrijski objekt. Geometrijski objekt tkanine se mijenja prolaskom vremena simulacije, dok čvrsti objekt zadržava svoju početnu definiciju kroz simulaciju. Sukladno tome, treba se pokloniti određena pažnja prilikom modeliranja strukture podataka za pojedini tip geometrijskih objekta.

Geometrijski objekt tkanine

Programski objekt koji sadrži informacije o geometrijskom objektu tkanine je implementiran kao proširenje virtualnog sučelja Entity. Uz informacije koje su definirane u tom sučelju potrebno je da ovaj objekt sadrži i podatke koje opisuju sam objekt tkanine. Te informacije su koeficijent unutarnjeg prigušenja, struktura čestica i njihova međusobna povezanost oprugama. Koeficijent unutarnjeg prigušenja je zapisan kao jedan broj s pomičnim zarezom, dok su za definiciju čestica i opruga korištene posebne strukture podataka.

Struktura podataka za opis čestice ima slijedeću definiciju u C++ programskom jeziku:

struct structVertex {
     math::Vector3 pos;
     math::Vector3 oldPos;
     float tu, tv;
     math::Vector3 normal;
     math::Vector3 speed;
     float mass;
     bool moveable;
     bool selected;
};

Opis sadržaja strukture čestice:

Struktura podataka za opis opruge ima slijedeću definiciju u C++ programskom jeziku:

struct structSpring {
     unsigned int v[2];
     float ks;
     float kd;
     float length;
     bool selected;
};

Opis sadržaja strukture opruge:

Da bi bilo moguće prikazati tkaninu pomoću OpenGL grafičke biblioteke potrebno je geometriju tkanine prikazati kao skup trokuta. Svaki trokut koji je potrebno iscrtati je predstavljen kao popis od tri čestice zapisane svojim rednim brojem u polju čestica.

struct structTriangle {
    unsigned int v[3];
};

Prilikom iscrtavanja objekta tkanine koriste se mogućnosti osvjetljenja i glatkog modela sjenčanja OpenGL biblioteke, što omogućava detaljniji prikaz geometrijskih objekata. Za implementaciju toga potrebno je, zajedno s pozicijom čestice tkanine, OpenGL biblioteci proslijediti i informaciju o normali na površinu u toj točci. Normale čestica se izračunavaju prije svakog iscrtavanja za slučaj da je došlo do promjene geometrije tkanine.

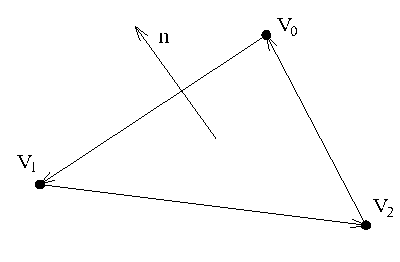
Slika 7. Orijentacija trokuta i njegova normala

Geometrijska definicija trokuta je prikazana na slici 7. Kako je svaki trokut zadan s tri pozicije čestice (, i) normalu ravnine u kojoj leži trokut se može izračunati kao:

Jedna čestica može biti vrh više trokuta, te se za izračun njene normale moraju uzeti u obzir normale svih tih trokuta. Konačna vrijednost normale u čestici se dobije normalizacijom sume normala svih trokuta kojima zadana čestica predstavlja jedan od vrhova:

gdje je:

•  - normala u čestici
•  - normala trokuta kojem je zadana čestica jedan od vrhova

Informacije o strukturi čestica i opruga su zapisane u obliku kontinuiranih polja gore opisanih struktura. Takav način zapisa omogućuje jednostavan i brz pristup bilo kojem elementu polja koristeći samo njegov redni broj u polju.

Struktura podataka za opis podataka tkanine ima slijedeću definiciju u programskom jeziku C++:

struct clothData {
    float damping;
    structVertex *vertices;
    unsigned int verticesCount;
    structSpring *springsStructural,
        *springsShear, *springsBend;
    unsigned int springsStructuralCount,
        springsShearCount, springsBendCount;
    structTriangle *triangles;
    unsigned int trianglesCount;
};

Opis sadržaja gornje strukture:

Čvrsti geometrijski objekt

Programski objekt koji sadrži informacije o čvrstim geometrijskim objektima je također implementiran kao proširenje virtualnog sučelja Entity. Pozicioniranje objekta se postiže postavljanjem transformacijske matrice definirane u Entity sučelju. Prilikom učitavanja geometrijskog objekta iz 3DS datoteke kreira se OpenGL prikazna lista (eng. display list) koja se koristi za iscrtavanje objekta, te se za potrebe razrješavanja sudara pohrane vrijednosti točaka i normala koje definiraju geometriju objekta.

Simulacija

Svaka simulacija započinje iz nekog unaprijed definiranog stanja mirovanja. U tom stanju je brzina svake pojedine čestice tkanine jednaka nula, a njihov smještaj u krajnjem geometrijskom sustavu je definiran kao kombinacija njihovog smještaja u referentnom geometrijskom sustavu objekta te transformacijske matrice koja objekt tkanine preslikava u krajnji geometrijski sustav. Zbog pojednostavljenja implementacije potrebno je, prije početka simulacije, sve čestice objekata tkanine preslikati u krajnji geometrijski sustav tako što se svaki pojedini vektor koji definira njihovu poziciju u geometrijskom sustavu objekta tkanine transformira matricom transformacije pojedinog objekta. Svaka operacija simulacije se dalje provodi na objektima tkanine definiranima u krajnjem geometrijskom sustavu.

Proces simulacije se dalje provodi pojedinačno za svaki okvir (eng. frame) animacije. U tome procesu se na osnovu trenutnog stanja u sustavu i u ovisnosti o vremenskom intervalu proteklom između dva okvira određuje novo stanje sustava. Vremenski interval protekao između dva okvira animacije se koristi kao korak  pri traženju rješenja diferencijalnih jednadžbi, pa se zbog stabilnosti sustava mora paziti na njegovu vrijednost. Posebno se treba naglasiti činjenica da prilikom izvođenja simulacije u stvarnom vremenu minimalna vrijednost vremenskog intervala između dva okvira ( i ) jednaka je vremenu potrebnom za provođenje simulacije okvira  (slika 8).

Slika 8. Raspodjela vremenskih odsječaka pri simulaciji u stvarnom vremenu

Na slici 8 je primjer simulacije u stvarnom vremenu, na kojoj  označava vrijeme potrebno da se izračuna stanje sustava u koraku , predstavlja vrijeme provedeno obavljajući ostale zadatke koji nisu vezani za izračun stanja (npr. iscrtavanje slike). Ukupno vrijeme provedeno za obavljanje tih zadataka predstavlja najmanje moguće vrijeme prije nego se započne računanje slijedećeg stanja sustava. S obzirom da se radi o simulaciji u stvarnom vremenu u koraku  korak simulacije će iznositi . U tom slučaju se lako može dogoditi, pogotovo kod složenijih simulacijskih okruženja, da se prilikom simulacija primijete nestabilnosti u numeričkim metodama rješavanja diferencijalnih jednadžbi.

Proces simulacije se provodi rješavanjem dviju diferencijalnih jednadžbi prvog stupnja za svaku česticu u geometrijskom objektu tkanine. Da bi se moglo pristupiti rješavanju diferencijalnih jednadžbi potrebno je prvo odrediti iznose sila koje djeluju u sustavu čestica i opruga. Prilikom računanja stanja sustava u novom koraku  koriste se informacije o stanju sustava u koraku  da bi se izračunale sile opruga koje djeluju na pojedinu česticu. Sile opruga se računaju koristeći informacije o oprugama i poziciji čestica koristeći Hookov zakon (1). Dobivenim vrijednostima se pridodaju unutarnja sila prigušenja (2), te vanjske sile gravitacije (6) i toka fluida (7). Ukupni rezultat takve operacije je dan formulom (8). U slučaju da je čestica označena kao nepokretna vrijednost sile koja djeluje na nju se postavi na nulu.

Nakon izračuna sila za pojedinu česticu potrebno izračunati ubrzanje točke (9), te numeričkom metodom rješavanja dviju diferencijalnih jednadžbi (10) odrediti njen novi položaj uzimajući u obzir mogućnost postojanja sudara s čvrstim objektima u simulacijskom okruženju.

Eulerova integracija

Eulerov algoritam je najjednostavniji algoritam za numeričku integraciju diferencijalne jednadžbe. Pri izračunu stanja u koraku  se koriste sile izračunate u koraku  i slijedeće jednadžbe:

gdje je:

•  - vremenski korak integracije
•  - masa čestice
•  - suma svih sila koji djeluju na česticu
•  - brzina čestice u koraku
•  - brzina čestice u koraku
•  - pozicija čestice u koraku
•  - pozicija čestice u koraku

Da bi odredila stanje na kraju vremenskog odjeljka ova metoda numeričke integracije koristi informaciju o stanju s početka odjeljka.

Runge-Kutta integracija

Za implementaciju Runge-Kutta metode numeričke integracije je uzeta metoda četvrtog stupnja prikazana formulama (49). Kako je potrebno izračunati rješenja dviju diferencijalnih jednadžbi prvoga stupnja, potrebno je dva puta primijeniti Runge-Kutta metodu.

Uvrštenjem jednadžbi (10) u skup jednadžaba odabrane Runge-Kutta metode dobiva se skup jednadžbi koji predstavljaju rješenje diferencijalne jednadžbe i određuje stanje tkanine u novom koraku simulacije.

gdje je:

•  - ubrzanje čestice
•  - brzina čestice
•  - pozicija čestice
•  - korak simulacije

Razrješavanje sudara

Za otkrivanje sudara u simulaciji korištena je biblioteka SOLID (http://www.dtecta.com) čija je svrha provođenje ispitivanja presijecanja i utvrđivanje blizine između geometrijskih objekata. Izvorni kod biblioteke je otvoren, pa je moguće izvest bilo kakve potrebne promjene.

Za rad s bibliotekom SOLID potrebno je definirati okruženje nad kojim će se vršiti ispitivanje sudara. Svaki objekt koji se želi uključiti u ispitivanje sudara se mora definirati kao zaseban objekt unutar toga okruženja. Za svaki čvrsti geometrijski objekt se definira novi objekt unutar okruženja biblioteke za otkrivanje sudara koji se koriti za razrješavanje sudara između objekta tkanine i čvrstog objekta.

Biblioteka SOLID omogućuje dva različita pristupa problemu razrješavanja sudara između objekata. Prvi način je da se za svaki objekt definira funkcija za razrješenje koju će sama biblioteka zvati u slučaju sudara, dok je drugi način ispitivanje presjecišta proizvoljno zadane zrake s objektima u ispitivanom okruženju. Prilikom testiranja oba načina rada pokazalo se da je drugi način jednostavniji za implementaciju, a uz to ima i puno bolje vremenske performanse.

Otkrivanje sudara se provodi za pomak svake čestice pojedinačno. Nakon što se numeričkom metodom izračuna nova pozicija čestice koristeći funkcionalnost SOLID biblioteke provjerava se da li dužina određena prijašnjom i sadašnjom pozicijom siječe neki objekt u okruženju nad kojim se provodi ispitivanje sudara. U slučaju da dođe do presijecanja, SOLID biblioteka može dati informaciju o poziciji točke sjecišta dužine i čvrstog objekta, te normalu površine čvrstog objekta u točki sjecišta. Normala površine čvrstog objekta je definirana u krajnjem geometrijskom sustavu i uvijek pokazuje prema početnoj točki ispitne dužine, dok je mjesto presijecanja definirano parametrom  iz intervala  koji određuje točku na zadanoj dužini prikazanu u parametarskom obliku.

gdje je:

•  - pozicija sjecišta
•  - početna točka ispitne dužine
•  - krajnja točka ispitne dužine
•  - parametar iz intervala  koji određuje mjesto sudara na dužini

Prvotna ideja je bila da se razrješenje sudara može izvršiti tako da se nova pozicija čestice koja je izazvala sudar postavi na samu površinu objekta s kojim se sudarila.

gdje je:

•  - pozicija čestice u koraku
•  - pozicija čestice u koraku
•  - parametar koji određuje mjesto sudara na dužini

Međutim, s ovim rješenjem se javlja problem da na česticu i nakon prvotnog sudara djeluju sile, te se ona pomiče po samoj površini objekta. Nakon nekog vremena će, zbog nepreciznosti otkrivanja sudara u implementaciji biblioteke SOLID, čestica proći kroz čvrsti objekt bez da izazove sudar. Taj problem je prikazan na slici 9.

Da bi se sudar uspješno razriješio, implementirano je rješenje koje česticu, u slučaju sudara, vraća na poziciju koju je imala prije početka simulacijskog koraka:

Kako je, zbog preciznosti integracije, poželjno imati što manji korak simulacije  može se pretpostaviti da je i pomak čestice unutar jednog koraka dovoljno mali da se neće primijetiti nedostatci u preciznosti kod ovog rješenja.

Slika 9. Problemi s razrješenjem sudara nastalih zbog nepreciznosti otkrivanja sudara

Nakon promjene pozicije čestice koja je sudjelovala u sudaru potrebno je promijeniti i iznos njene brzine, jer smo skratili put koji je čestica prešla u istom vremenskom intervalu, što se u ovome slučaju vrlo jednostavno postiže postavljanjem njene vrijednosti na nulu.

Kako se u ovoj implementaciji otkrivanja i razrješenja sudara gleda samo putanja čestice, lako je moguće da, iako sama čestica na svome putu ne presječe niti jedan čvrsti objekt, trokut kojem ona pripada presječe čvrsti objekt, a ova metoda ne registrira taj sudar.

Slika 10. Pojava greške prilikom otkrivanja sudara

Na slici 10 se može vidjeti primjer nastajanja greške prilikom otkrivanja sudara. U ovom slučaju je trokut tkanine prikazan kao veći osjenčani trokut određen vrhovima V0, V1 i V2, a trokut koji predstavlja čvrsti objekt je prikazan kao manji osjenčani trokut. Prilikom jednog koraka simulacije vrh V0 promjeni položaj u položaj označen kao V0', a trokut tkanine poprimi položaj definiran vrhovima V0', V1 i V2 prikazan isprekidanim linijama. Prilikom promjene položaja trokuta tkanine je došlo do prolaska tog trokuta kroz trokut čvrstog objekta, ali se taj sudar nije otkrio. Do otkrivanja sudara nije došlo zato što se gornji algoritam otkrivanja sudara zasniva na traženju presjecišta putanje čestice i čvrstih objekata, a u ovom primjeru ne dolazi do presijecanja čvrstog tijela dužinom. Broj ovakvih pogrešaka se može smanjiti, ali ne i u potpunosti eliminirati, promjenom geometrijske strukture objekta tkanine ili čvrstog objekta. U gornjem primjeru se može problem smanjiti povećanjem gustoće čestica u objektu tkanine. U tom slučaju će i izgled tkanine biti detaljniji, a i rezultati sudara će izgledati mnogo realnije.

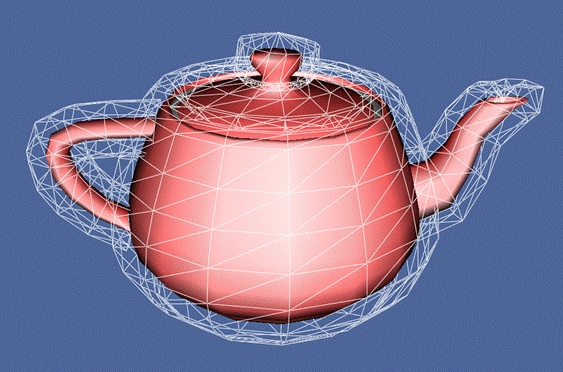
Slika 11. Prikaz čvrstog objekta i pripadajućeg objekta za ispitivanje sudara

Na slici 11 je prikazana geometrija jednog čvrstog objekta. Ožičenjem je prikazan objekt definiran u okruženju SOLID biblioteke koji će se koristiti za otkrivanje sudara. Prilikom simulacije se pojavljuje gore opisani problem kod detekcije sudara pa na nekim mjestima dolazi do prodiranja čvrstih objekata kroz objekt tkanine.

Slika 12. Prikaz greške otkrivanja sudara

Na slici 12 je prikaz gore opisane greške koja nastaje prilikom otkrivanja sudara čestica s geometrijom čvrstog objekta. Prilikom simulacije neke od čestica nisu ostvarile kontakt s čvrstim objektom već su došle u takvu poziciju da djeluje kao da je čvrsti objekt čajnika probio kroz tkaninu. Ovaj problem se može izbjeći promjenom geometrije definirane za otkrivanje postojanja sudara.

Prilikom učitavanja geometrije čvrstog tijela iz 3DS datoteke dostupne su informacije o točkama koje definiraju geometrijski objekt, te informacije o normalama na površinu u određenoj točci. Ako se pretpostavi da svaka točka ima samo jednu normalu, tj. Kontinuiranu prvu derivaciju, može se kreirati novi geometrijski objekt koji će imati istu strukturu kao izvorni objekt, ali će svaka točka biti pomaknuta u smjeru pripadajuće normale za neki unaprijed zadani faktor .

gdje je:

•  - početna pozicija točke
•  - krajnja pozicija točke
•  - normala u zadanoj točki
•  - faktor proširenja

Takvim postupkom se definira novi geometrijski objekt koji će se koristiti samo pri otkrivanju sudara, dok se u iscrtavanju koristi izvorni objekt.

Slika 13. Prikaz čvrstog objekta i pripadajućeg objekta za ispitivanje sudara uz faktor proširenja

Slika 14. Prikaz izbjegavanja greške prilikom otkrivanja sudara

Na slici 14 se može primijetiti da je su rezultati dobiveni ovakvom metodom otkrivanja sudara puno prihvatljiviji od prijašnjih rezultata, ali su i sami izvor dodatnih problema. Za primjer na slici 14 je izabran faktor proširenja od , jer je tek za tako veliki faktor prestalo probijanje čvrstog objekta preko tkanine. Međutim, novi problem se stvara zato što je taj faktor proširenja korišten za proširenje cijelog objekta, pa se na nekim mjestima pojavljuje veliki odmak tkanine od same geometrije čvrstog objekta. Detaljnije je taj problem prikazan na slici 15.

Slika 15. Greška nastala zbog istog faktora proširenja korištenog na cijelom objektu

Drugi problem ovog načina implementacije je taj da jedino radi na geometrijskim objektima koji zadovoljavaju uvjet da su C1 neprekinuti, tj. da svaki vrh ima jednu normalu. Problem se može prikazati na geometrijskom objekta koji je samo C0 neprekinut.

Slika 16. Geometrijsko proširenje C0 kontinuiranog objekta

Kako je piramida na slici 16 C0 neprekinuti geometrijski objekt znači da kod nje postoje vrhovi s više od jedne normale. Kod piramide svaki vrh stranice ima onoliko normala koliko se stranica u njemu dodiruje. Ako se ovaj objekt proširi, dobije se objekt koji je potpuno beskoristan pri otkrivanju sudara.
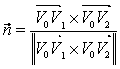