Klasifikatorski Sustavi


- Mario Lučić - mario.lucic@fer.hr
- Goran Radanović - goran.radanovic@fer.hr
Klasifikatorski sustavi sa sposobnošću učenja, Projekt, Mario Lučić, Goran Radanović
Klasifikatorski sustavi s mogućnošću učenja pravila jednostavne igre, Završni rad, Mario Lučić
- Rad - PDF: LogicGames [PDF]
- Prezentacija - PPT: LogicGames [PPT]
- Programsko rješenje - RAR: LogicGames [RAR]
ZCS i XCS klasifikatorski sustavi, Završni rad, Goran Radanović
- Rad - PDF: ZCSXCS [PDF]
- Programsko rješenje - RAR: ZCSXCS [RAR]
Klasifikatorski sustavi sa sposobnošću učenja
1.Uvod
2.Pregled klasifikatorskih sustava
2.1 Podjela LCS-a
2.2 Michiganski stil LCS-a
2.3 Pittsburghski stil LCS-a
2.4 Stil iterativnog učenja pravila
3. Podrobniji pogled u model michiganskog stila LCS-a
3.1 Kratak pogled na genetske algoritme
3.2 Kratak pogleg na učenje potkrjepljenjem
3.3 Model LCS-a
4. Porodice michiganskog stila LCS-a
4.1 ZCS
4.2 XCS
5. Primjena LCS-a
6. Literatura
Povećanje kompleksnosti mnogih problemskih domena dovelo je do potrebe za rješenjima koje se mogu prilagoditi pojedinom zadatku. Korištenjem evolucijskih algoritama i učenja s potkrjepljenjem modeliraju se sustavi koji imaju mogućnost prilagođavanja. Klasifikatorski sustavi s mogućnošću učenja (eng. Learning Classifier Systems) bazirani na pravilima su jedna od evolucijskih tehnika. Cilj LCS-a je implicitno pronaći funkciju koja preslikava skup stanja okoline na skup pravila sustava koja će maksimi zirati ukupnost nagrada primljenih od okoline.
Evolucijski algoritmi bazirani su na Darwinovim principima preživljavanja najspremnijih, dok sama populacija pravila predstavlja skup rješenja klasifikacijskog problema. Uz pomoć genetskih algoritama nad populacijom se vrše stohastički procesi mutacije gena i rekombinacije. Ideja zajednička svim evolucijskim metodama je pretraživanje problemskog prostora evoluirajući početni nasumce odabrani skup rješenja tako da na kraju svakog koraka skup rješenja bude kvalitetniji, tj. prilagođeniji problemu. Cilj svake jedinke je opstati, dok je cilj sustava ukloniti one jedinke koje ne pridonose maksimiziranju nagrada dobivenih iz okoline. Učenje s potkrjepljenjem, preslikano iz Pavlov-ljevih metoda u psihologiji, postiže se metodom pokušaja i promašaja uz nagrade ili kazne od strane okoline. Sustav se kroz niz iteracija prilagođava okolini i nakon određenog vremena jedna jedinka ili populacija jedinki evoluira u rješenje klasifikacijskog problema.
Područija primjene LCS-a odnose se na modeliranje i optimizaciju, inteligentnu analizu podataka (eng.Data Mining) i upravljanje procesima.
vrh 2. Pregled klasifikatorskih sustava
Klasifikatorski sustavi (Classifier systems, CS, CFS) su sustavi temeljeni na skupu
pravila (klasifikatora) koja određuju reakciju sustava na uvjete dane u njegovoj
okolini. Klasifikatorki sustavi se dijele na klasifikatorske sustave koji nemaju
sposobnost učenja (non-learning classifier systems, nLCS) i klasifikatorske sustave
koje imaju sposobnost učenja (learning classifier systems, LCS) [10].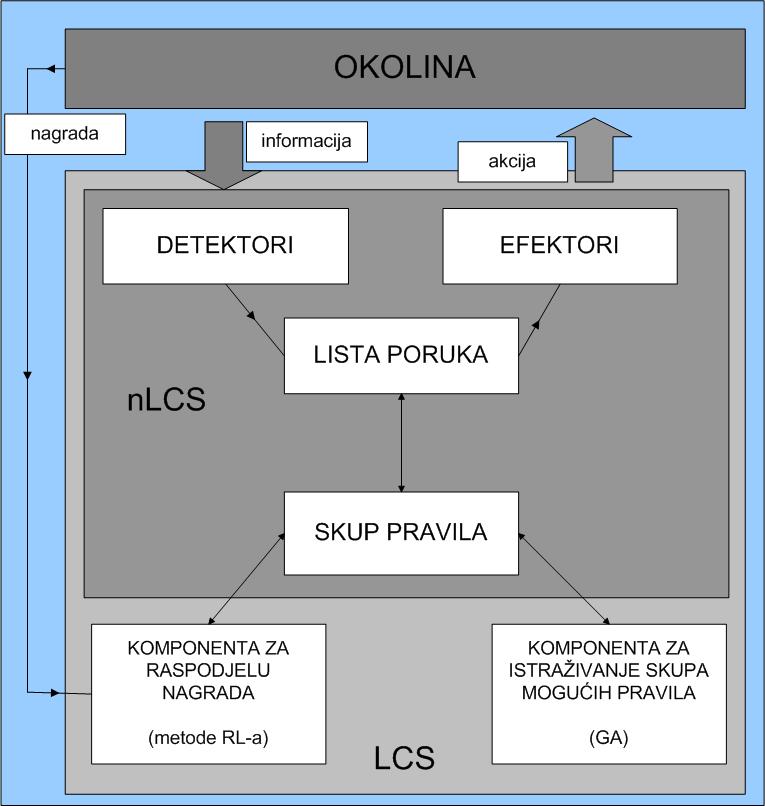
nLCS je sustav sastavljen od detektora, efektora, liste poruka i skupa pravila oblika uvjet (uvjeti) : akcija značenja ako uvjet (uvjeti) onda akcija. Pomoću detektora se prenosi stanje okoline u listu poruka. Zatim se iz skupa pravila izabire pravilo čiji uvjet odgovara sadržaju liste poruka. Akcija koju sustav treba izvesti određena je pravilom i njome se puni lista poruka. U zadnjem koraku se, pomoću efektora, izvodi akcija smještena u listi poruka [2]. Ukoliko se nLCS proširi komponentom za raspodjelu nagrada primljenih od okoline i komponentom za istraživanje prostora mogućih pravila, dobivamo LCS [9]. Cilj LCS-a je odrediti takav skup pravila kojim će se maksimizirati nagrade primljene od okoline. Treba napomenuti da je ovakvim proširenjem dobiven michiganski stil LCS-a.
vrh 2.1 Podjela LCS-a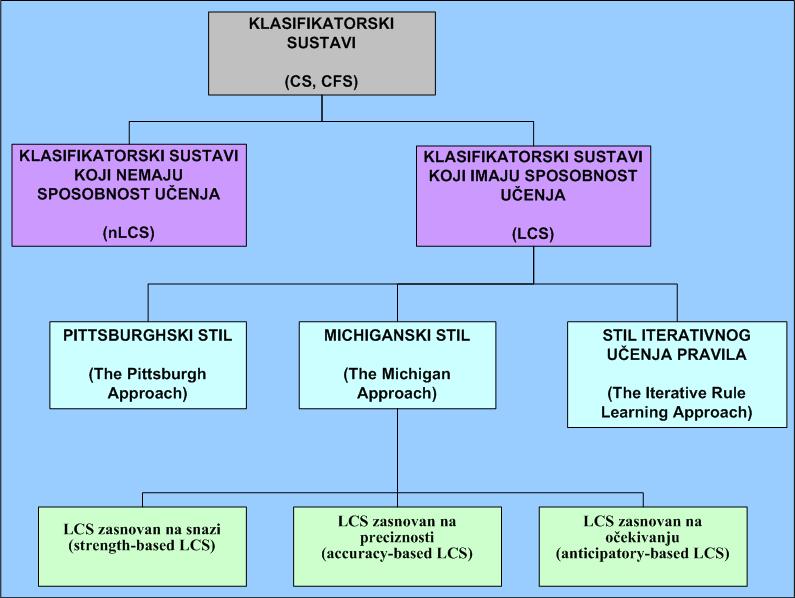
LCS je prvi opisao J. Holland 1975. kao sustave koji posjeduju kognitivne značajke [3], [4]. Tijekom 1980-tih isprofilirala su se dva stila (pristupa) LCS-a. Holland i njegovi suradnici oblikovali su na Sveučilištu Michigan michiganski stil (The Michigan Approach), dok je Smith sa svojim suradnicima na Sveučilištu Pittsburgh oblikovao pittsburghski stil (The Pittsburgh Approach) [2]. Uz michiganski i pittsburgski stil postoji i stil iterativnog učenja pravila (The Iterative Rule Learning Approach), prvi puta primijenjen na SIA sustavima (Venturini, 1993) [14]. Podjela CS-a i LCS-a prikazana je na slici 2.2.
vrh 2.2 Michiganski stil LCS-aMichiganski stil LCS-a karakterizira kombinacija učenja potkrjepljenjem (Reinforcement Learning, RL) i genetskog algoritma (Genetic Algorithm, GA). RL je tehnika učenja pokušajima i pogreškama putem primljenih nagradama, a u LCS-u predstavlja komponentu za raspodjeljivanje nagrada primljenih od okoline [3]. GA je heuristička metoda optimizacije temeljena na evolucijskom procesu, a u LCS-u predstavlja komponentu za istraživanje prostora mogućih pravila.
Ono što bitno razlikuje michiganski stil LCS od nekih drugih (klasičnih) tehnika RL-a je sposobnost generalizacija pravila: postoje pravila koja predstavljaju više stanja okoline čime se smanjuje broj pravila kojima sustav treba raspolagati. Ipak, treba naglasiti da prevelika generalizacija nije dobra: može dovesti do pojave da generalizirana pravila izbace specijalizirana pravila koja bolje odgovaraju na određeno stanje okoline [1]. U michiganskom stilu svaka jedinka predstavlja jedno pravilo. Evolucija i optimizacija pravila se obavlja lokalno, tj. na pojedinim pravilima. Sustav nagrade iz okoline neposredno raspodjeljuje jedinkama (pravilima) čije su akcije nagrađene, a posredno i jedinkama (pravilima) čije su akcije prethodile nagrađenim akcijama.
Za dobivanje sustava koji će optimalno reagirati na stanja okoline, potrebno je uravnotežiti odnos potreba pojedine jedinke (pravila) i potrebe cijelog sustava [12]. Potreba jedinke (pravila) se očituje u tome da opstane, tj. ne bude eliminirana GA-om. To znači da svaka jedinka treba težiti dobivanju što većeg dijela nagrade. S druge strane, potreba sustava je da jedinke (pravila) zajedno djeluju na ispravan način. To znači da se nagrada dobivena određenom akcijom treba rasporediti ne samo na pravila koja su neposredno uzrokovala akciju, već i na ona pravila koja su dovela do stanja okoline u kojem je izvedena ta akcija.
Shematski prikaz michiganskog stila LCS-a (i njegovog odnosa sa nLCS-om) dan je na slici 2.1. Michiganski stil LCS-a pripada on-line sustavima i uči na temelju jedne instance problema [11]. Stil je pogodan za opisivanje sustava u stvarnom vremenu (real-time systems) gdje nagle promjene ponašanja nisu dozvoljene [12]. Tri su porodice michiganskog stila LCS-a:
- LCS zasnovan na snazi (strength-based LCS)
- LCS zasnovan na preciznosti (accuracy-based LCS)
- LCS zasnovan na očekivanju (anticipatory-based LCS).
Pittsburgski stil LCS-a kombinira metode učenja pod nadzorom (Supervised Learning, SL) sa GA-om. SL je tehnika strojnog učenja koja stvara odgovarajuću funkciju na temelju skupa za učenje (training set) sastavljenog od primjera oblika ulaz-izlaz (input-output) [5]. Cilj sustav koji uči SL tehnikom je, nakon što prođe kroz primjere zadane u skupu za učenje, predvidjeti željeni izlaz za odgovarajući ulaz.
Za razliku od michiganskog stila, u pittsburghskom stilu svaka jedinka predstavlja
rješenje klasifikacijskog problema [14]. Istovremeno se raspolaže s nekoliko skupova
pravila i to tako da jedna jedinka predstavlja jedan skup pravila. Pravila su fiksirane
duljine, ali jedna jedinka može sadržavati različiti broj pravila pa je jedinka
promjenjive duljine. Dozvoljene su i generalizirana pravila. Nad skupom jedinki
se pokreće GA čije su operacije rekombinacije, mutacije i selekcije prilagođene
promjenjivim duljinama jedinki. Funkcija procjene (dobrote) određuje kvalitetu pojedine
jedinke (skupa pravila) na temelju poklapanja pravila iz jedinke s primjerima za
učenje, tj. na temelju točnosti kojom jedinka obavlja klasifikaciju. Prilikom određivanja
kvalitete mogu se uključiti i neke posebne karakteristike jedinke poput njene duljine.
Trajanje procesa učenja zadano je evolucijskim
 vremenom GA-a.
vremenom GA-a.
Model Pittsburghskog stila LCS-a je prikazan na slici 2.3. Pittsburghski stil LCS-a pripada off-line sustavima i uči iterativno na temelju skupa instanci problema [11]. Optimizacija se provodi globalno nad skupovima pravila, a ne nad pojedinačnim pravilima kako je to slučaj u michiganskom stilu. Zbog predstavljanja cijelog skupa pravila jednom jedinkom, veliki problem predstavljaju zahtijevane količine memorije i procesorskog vremena [12].
Problem učenja u pittsburghskom stilu je doslovno sveden na optimizaciju GA-om, zbog čega je i upitno je li ovaj stil bliži samom GA-u ili LCS-u. Tipični predstavnici pittsburghskog stila LCS-a su algoritmi GABIL i GIL [14].
vrh 2.4 Stil iterativnog učenja pravila
Stil iterativnog učenja pravila se temelji na pristupu podjeli pa vladaj. Kao u
michiganskom stilu, jedna jedinka predstavlja jedno pravilo, dok se sličnosti sa
pittsburghskim stilom pronalaze u kombiniranju SL-a sa GA-om.
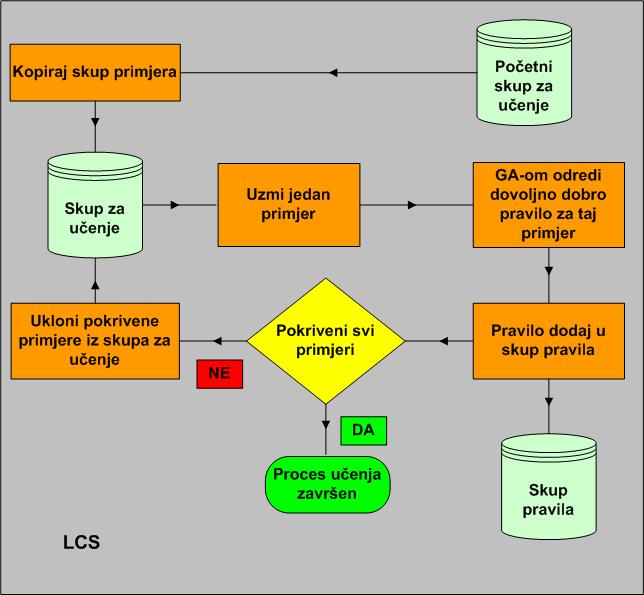
Sustav opisan stilom iterativnog učenja pravila uči skupom primjera koji se nalaze u skupu za učenje. Učenje traje sve dok skup pravila ne pokrije zadane primjere. U svakom koraku se uzima nepokriveni primjer i uz pomoć GA-a se određuje dovoljno dobro pravilo za taj primjer. Ukoliko pravilo ne postoji u skupu pravila, ono se nadodaje, a iz skupa za učenje se brišu primjeri koji su pokriveni postojećim skupom pravila. Opisani ciklus se ponavlja dok god ima primjera u skupu za učenje. Funkcija procjene (dobrote) uzima u obzir generalizaciju (što veću pokrivenost primjera) i preciznost predviđanja pojedinih pravila.
Model LCS-a temeljen na stilu iterativnog učenja pravila je prikazan na slici 2.4. Predstavnik ovoga stila je HIDER sustav [13], [14].
3. Podrobniji pogled u model michiganskog stila LCS-aHolland i Reitman su 1978. izložili prvu implementaciju LCS-a [3]. Iako je Hollandova verzija LCS-a bila implementirana i u rješavanju stvarnih problema, ona se pokazala složena za izvedbu i nešto kasnije našla je dobru zamjenu u jednostavnijim verzijama LCS-a. Ovdje se gradi model LCS-a koji se dijelom oslanja na izvornu verziju Hollandovog LCS-a. Zbog boljeg razumijevanja načina rada LCS-a, prethodno je potrebno ukratko opisati GA i RL.
3.1 Kratak pogled na genetske algoritme
Genetski algoritam (Genetic Algorithm, GA) je heuristička metoda optimizacije zasnovana na principima Darwinove teorije evolucije. Algoritam je baziran na populaciji rješenja i kroz niz koraka nastoji poboljšati populaciju tako da na kraju evolucijskog procesa najbolja jedinka populacije predstavlja dovoljno dobro rješenje optimizacijskog problema.
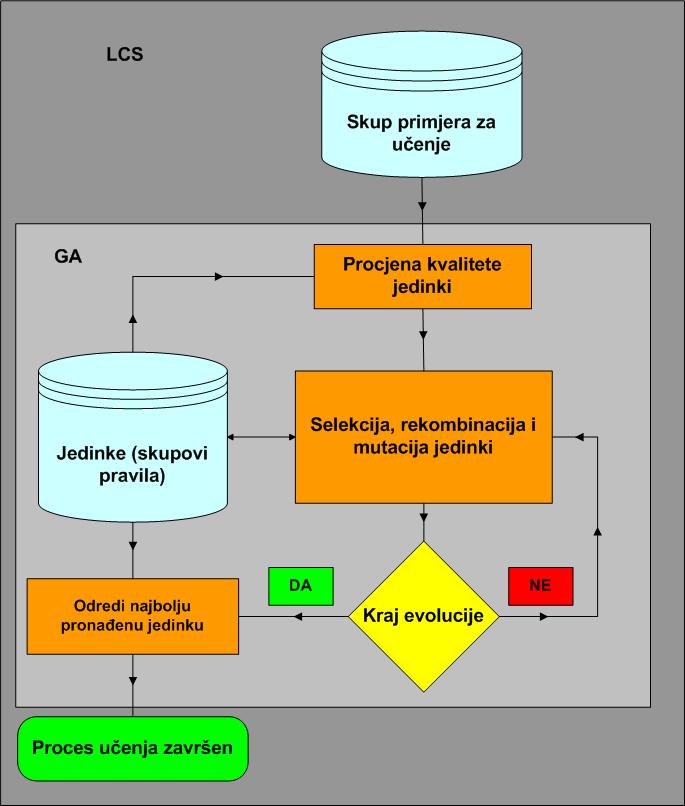
Ne ulazeći u detalje GA-a, treba spomenuti da se u michiganskom stilu LCS-a upotrebljava eliminacijski GA (steady-state GA) opisan na slici 3.1.
GA, koji je prvobitno bio tek dio LCS-a, s vremenom se počeo promatrati kao poseban algoritam i postao je mnogo popularniji od LCS-a [2]. U LCS-u GA ima funkciju istraživanja prostora mogućih pravila. Pri tome se uz GA mogu primijeniti i neke druge heurističke metode [3].
vrh 3.2 Kratak pogleg na učenje potkrjepljenjemUčenje potkrjepljenjem (Reinforcement Learning, RL) temelji se na operantnom uvjetovanju (teoriji učenja u psihologiji), a odnosi se na područje strojnog učenja (machine learning) koje proučava kako agent treba djelovati u promatranoj okolini da bi primio što veću nagradu od okoline [5]. Riječ je o učenju nagradama i kaznama (uz pokušaje i pogreške). Za svaki dobar odgovor na stanje u okolini, okolina nagrađuje sustav, dok se loši odgovori kažnjavaju. Formalnije se RL definira:
- Skupom akcija A
- Skupom stanja okoline S
- Skupom nagrada (najčešće je to skup {0 ,1} ili interval realnih brojeva) [7].
U svakom trenutku (koraku) t sustav na temelju stanja okoline si (si ϵ S) odabire akciju a iz skupa mogućih akcija A. Okolina mijenja stanje st u st+1 te daje sustavu nagradu rt. Cilj sustava je odrediti funkciju pravila π: S→A koja preslikava skup stanja okoline u skup akcija sustava tako da se maksimizira ukupnost nagrada okoline. U LCS-u RL ima funkciju raspoređivanja korisnosti pojedinim pravilima [3].
vrh 3.3 Model LCS-aKao što je već rečeno, LCS se temelji na skupu pravila. Skup pravila (klasifikatora) su oblika uvjet:akcija značenja ako uvjet onda akcija. Drugim riječima, izborom pravila koje zadovoljava uvjet okoline određena je akcija prema okolini.
Uvjet je u najjednostavnijem slučaju niz znakova iz ternarnog skupa {0, 1, #} pri čemu znak # predstavlja i 0 i 1 (tzv. don't care znak). Primjerice, uvjet 1# predstavlja i uvjet 10 i uvjet 11. Time je omogućena generalizacija (općenitost) pravila. U ovisnosti o pojedinim akcijama, okolina nagrađuje sustav. Kako bi sustav s vremenom usvojio dobra pravila, a loša pravila izbacio, potrebno je nekako označiti kvalitetu pojedinog pravila. Zbog toga je, uz uvjet i akciju, u pravilo potrebno dodati i veličina koja ima značenje korisnosti pravila. Time pravilo poprima oblik uvjet:akcija→korisnost. Proces koji se vrši je iterativan i opisuje se sljedećim koracima:
- Stanje okoline se pomoću detektora prenosi u listu poruka i to u dio koji namijenjen za pohranjivanje stanja okoline. Lista poruka, uz dio namijenjen za stanje okoline, ima i dio namijenjen za interne poruke te dio namijenjen za akcije. Interne poruke nose informacije o prethodnim stanjima okoline i prethodnim akcijama sustava.
- Za svako pravilo utvrđuje se odgovara li uvjet trenutnom stanju liste poruka i to na temelju dijela liste poruka namijenjenom za pohranjivanje stanja okoline i dijela za interne poruke. Uvjeti koji odgovaraju trenutnom stanju liste poruka stavljaju se u podudarni skup (match set, [M]). Ukoliko je skup [M] prazan, stvara se novo pravilo s uvjetom koji odgovara trenutnom stanju liste poruka.
- Pravila iz skupa [M] razvrstavaju se u skupine tako da pravila s istom akcijom pripadaju istoj skupini. Na temelju korisnosti svih pravila pojedine skupine predviđaju se nagrade pojedinih akcija i izabire se akcija. Pravila iz skupine iz koje je odabrana akcija se smještaju u akcijski skup (action set, [A]).
- Akcija se šalje u listu poruka namijenjenu za akcije, a obnavlja se dio liste poruka namijenjen za interne poruke. Efektori šalju akcije okolini.
- Obnavlja se dio pravila koji određuje korisnost (kvalitetu). Onim pravilima koji ne pripadaju skupu [A], a pripadaju skupu [M], reducira se korisnost. Pravila iz skupa [A] i ona koja su u nekoliko prijašnjih koraka pripadala skupu [A] međusobno raspodjeljuju korisnost.
- Primljena nagrada od okoline, koja se periodički šalje sustavu, raspoređuje se (jednoliko) među pravilima skupa [A]. Uzevši u obzir i 5. korak, pravila koja prethode pravilima koja su (prije) nagrađivana također poprimaju veću korisnost.
- Periodički ili s određenom vjerojatnošću pokreće se GA nad cijelim skupom pravila
(skup [N]), nad skupom [M] ili nad skupom [A]. Najčešće se koristi eliminacijski
GA (steady-state GA) [1], [3].
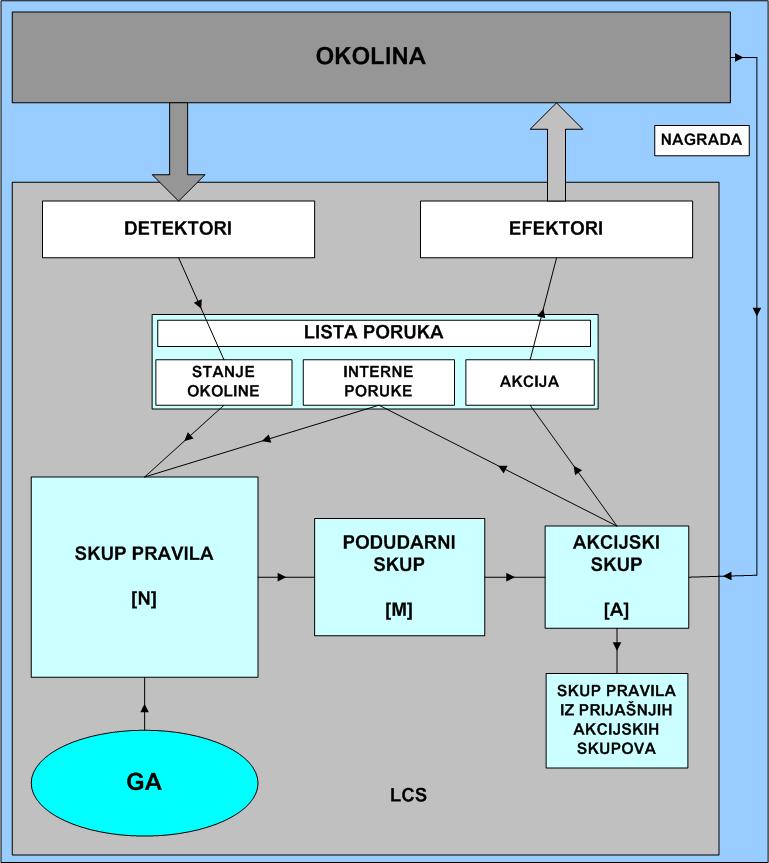
Ovim modelom opisana je struktura LCS-a. Bitna načela koje LCS treba slijediti su:
- Pronaći skup pravila koji za što veći broj mogućih uvjeta okoline sadrži pravilo koje donosi dovoljno veliku nagradu okoline. Posebice se to odnosi na pravila koja daju akcije za često pojavljivane uvjete okoline.
- Generalizirati skup pravila tako da uvjet jednog pravila odgovara što većem broju stanja uokolini. Pritom treba paziti da se ne izbace specijalizirana pravila koja daju bolje akcije na određeno stanje okoline nego neka generalizirana pravila.
- Ostvariti natjecanje među pravilima, ali samo onima koji imaju korespondentne dijelove uvjeta, tj. mogu odgovoriti na isto stanje okoline. Ostvariti princip da se ulančano nagrađuju pravila, tako da se nagrade i ona pravila čije su akcije prethodile nagrađenim akcijama, a ne samo pravila koja su neposredno uzrokovala nagrađenu akciju [1].
Kao što je već spomenuto, michiganski stil LCS-a se dijeli na tri porodice: LCS zasnovan na snazi (strength-base LCS), LCS zasnovan na preciznosti (accuracy-based LCS) i LCS zasnovan na očekivanju (anticipatory-based LCS).
LCS zasnovan na snazi(strength-based LCS) je najjednostavnija porodica michiganskog stila. Korisnost pojedinog pravila je određena skalarnom veličinom zvanom snaga. Snaga predstavlja procjenu nagrade koje će sustav primiti od okoline ako se ponaša u skladu s promatranim pravilom. Pomoću snage vršimo i procjenu pojedinog pravila budući da je to jedina veličina po kojoj možemo odrediti kvalitetu pravila. No ovakav pristup i nije baš najbolji. Naime, pravila koja uzrokuju ranije akcije mogu u početku izvršavanja algoritma poprimiti neproporcionalno velike iznose snage [1]. Također, zapostavljena su pravila koja dovode do manje nagrade iako ona mogu u određenoj okolnosti biti najbolji izbor [1].
Naposljetku, najveći problem predstavljaju previše generalizirana pravila koja često vode suboptimalnom rješenju [2]. Naime, pravila koja su više generalizirana imaju veću vjerojatnost pojavljivanja u skupu akcija (skup [A]) pa im snage poprimaju znatno veće vrijednosti nego manje generaliziranim pravilima iako im predviđanje nagrada okoline može biti nepreciznije. Ipak, za mnoge aplikacije ova porodica LCS-a je sasvim prihvatljiva. Najpoznatiji predstavnik ove porodice je ZCS.
LCS zasnovan na preciznosti (accuracy-based LCS) nadopunjuje korisnost pravila sa procijenjenom pogreške koju pravilo čini pri procjeni nagrade. Kvalitetu pravila više ne određuje snaga, već nova veličina povezana sa preciznosti pravila i to tako da su preciznija pravila kvalitetnija. Iako je sustav postao složeniji, uvođenjem spomenutih parametara sprječava se prevelika generalizacija pravila, a time je i prostor mogućih pravila učinkovitije prekriven. Najpoznatiji predstavnik ove porodice LCS-a je XCS.
LCS zasnovan na očekivanju (anticipatory-based LCS) prikazuje pravila u obliku uvjet:akcija→očekivanje pri čemu očekivanje predstavlja očekivano stanje okoline nakon primijenjene akcije na okolinu stanja uvjeta. Ovakva vrsta pravila (klasifikatora) gradi model prijelaza (model of transitions) [2]. Očekivanje može, ovisno o verzijama LCS-a, sadržavati i posebne znakove "=" i "?". Znak "=" označava da se atribut stanja okoline ne mijenja, dok znak "?" označava da se atribut stanja ne može predvidjeti [2]. Primjerice, ako na stanje okoline 101 djelujemo akcijom 0, tada pravilo #01:0→=1= predviđa stanje okoline 111.
Znak "?" je sličan znaku "#" (don't care) koji se pojavljuje u uvjetnom dijelu pravila. Na oblik pravila uvjet:akcija→očekivanje dodaju se parametri koji predstavljaju kvalitetu pojedinog pravila. Kvaliteta jedinke (pravila) je određena preciznošću predviđanja sljedećeg stanja okoline [15]. Jedan od poznatijih predstavnika ove porodice LCS-a je ACS2.
vrh 4.1 ZCSNajpoznatiji predstavnik LCS-a zasnovanih na snazi (eng. Fitness) je ZCS [1]. Kao i osnovni model LCS-a, opisao ga je Wilson. Naziv mu dolazi od imena „zeroth level LCS“. Uveden je zbog očitih prednosti nad opisanim osnovnim modelom LCS-a, posebice jednostavnosti razumijevanja i poboljšanja performansi. Parametar koji u ovom slučaju predstavlja kvalitetu pravila je snaga. Također, pravila koja odgovaraju trenutnom stanju okoline i imaju istu akciju spadaju pod istu klasu. Stoga se odabir i kasnije ažuriranje snage pojedinih pravila odvija nad svim pravilima u istoj klasi. Kako bi se osiguralo napredovanje sustava prema skupu jedinki koje maksimizira ukupnost nagrada iz okoline ZCS primjenjuje dvije heurističke tehnike generiranja novih jedinki: GA i „cover“ algoritam.
Eliminacijski GA, koji se pokreće nad svim pravilima, odabire dvije najbolje jedinke, tj. jedinke s najvećom snagom, te proizvodi dva potomka, koja potom mutira. Potomci se smještaju u skup svih pravila [N], a snaga im je određena polovinom snage roditelja. Također, dvije najslabije jedinke se uklanjaju iz skupa pravila [N]. U slučaju da je odgovarajući skup prazan ili da sadrži pravila čija je snaga manja od prosječne „cover“ algoritam generira novo pravilo koje odgovara trenutnom stanju okoline, a čija se akcija određuje nasumce. akon detekcije stanja okoline sva se odgovarajuća pravila smještaju u odgovarajući skup [M].
Nadalje, iz odgovarajućeg se skupa odabire pravilo koje ima najveću snagu – ono se sustavu čini kao trenutno najbolji izbor. Sva pravila koja imaju istu akciju kao i navedeno pravilo smještaju se u akcijski skup. Okolini se preko efektora prosljeđuje akcija definirana jedinkama u akcijskom skupu, i stanje okoline S mijenja se u stanje S+1. S ciljem realizacije učenja s potkjrepljivanjem u svakom koraku T pamti se trenutni akcijski skup.
Naime, u koraku T+1 sustav će nagraditi ili kazniti pravila koja su dovela do stanja okoline S+1 što je ključ čitavog procesa učenja. Uz to se u interni spremnik B sprema dio snage svakog pravila, tj. zbrojena snaga svih pravila pomnožena s nekom konstantom β. Potkrjepljenje se vrši na način da se snazi svakog pravila prethodnog akcijskog skupa dodaje jednak dio internog spremnika B*γ. Ukoliko sustav primi nagradu od okoline sva pravila trenutnog akcijskog skupa dobivaju jednak dio nagrade, tj. snaga pojedinog se poveća za δ*Nagrada podijeljeno s brojem pravila.
Nadalje, svim se pravilima koja su u skupu odgovarajućih pravila [M], a nisu u akcijskom skupu [A] smanjuje snaga za faktor τ da bi se u sljedećim koracima smanjila šansa za odabir istih. Formalno, ažuriranje snage u svakom koraku prikazano je jednadžbom:
-
F([A]) = F([A]) + β [ nagrada +γ*F([A+1]) – F([A])]
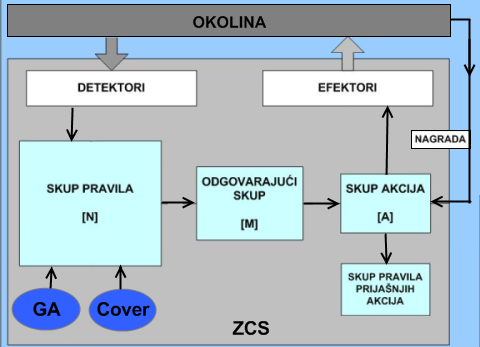
Usprkos dobrim performansama u većini poznatih problema, ZCS pokazuje izrazitu osjetljivost na parametre β , γ, δ i τ, pa se većina vremena utroši na njihovo konfiguriranje. Najpoznatije primjene navedenog sustava odnose se na inteligentne analize podataka ( eng. Data mining ) i modeliranje ekonomskih tržišta. Međutim, u uporabi ga je potpuno nadmašio predstavnik porodice sustava baziranih na preciznosti, XCS. Model ZCS-a prikazan je na slici 3.3.
vrh 4.2 XCS
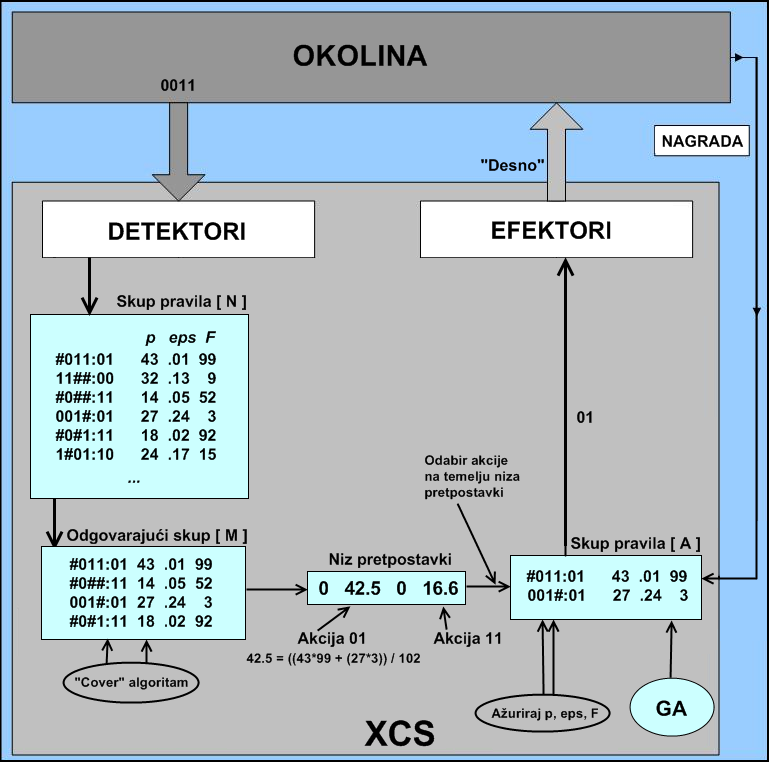
XCS pripada porodici klasifikatorskih sustava zasnovanih na preciznosti. Njegova
glavna razlika naspram ostalih modela je uvođenje dodatnih parametara kvalitete
pojedinog pravila: preciznost predviđanja „p“ i grešku pri predviđanju „ε“. Promatranjem
i ažuriranjem tri parametra u svakom koraku postiže se bolje tj. preciznije preslikavanje
skupa stanja okoline na skup pravila. Kao i u osnovnom
 modelu LCS-a,
u svakom koraku odgovarajući skup [M] sadrži pravila koja odgovaraju trenutnom stanju
okoline. Ukoliko je [M] prazan koristi se „cover“ algoritam koji će generirati odgovarajuće
pravilo.
modelu LCS-a,
u svakom koraku odgovarajući skup [M] sadrži pravila koja odgovaraju trenutnom stanju
okoline. Ukoliko je [M] prazan koristi se „cover“ algoritam koji će generirati odgovarajuće
pravilo.
Nadalje, za svaku se moguću akciju određuje njena „kvaliteta“ na temelju parametara pojedinih pravila koja su u klasi te akcije, te se sprema se u niz predviđanja. Akcija koja ima najveću vrijednost u tom nizu će preko efektora biti poslana okolini, a sva pravila koja su u klasi najkvalitetnije akcije biti će smještena u akcijski skup. Učenje s potkrjepljenjem sastoji se od ažuriranja parametara ε, p i F prema relativnoj preciznosti pojedinog pravila unutar skupa pravila kroz sljedećih pet koraka:
- Pogreška pri predviđanju svakog pravila se ažurira: εj= εj + β( |P - pj | - εj)
- Predviđanju svakog pravila se ažurira: pj = pj + β (P- pj)
- Preciznost svakog pravila κj se računa kao : κj= α(ε0 / ε)v ili κ=1(ε < ε0)
- Relativna preciznost svakog pravila κj' dobije se kao κj / ∑κi
- Relativna preciznost se koristi kako bi se ažurirala snaga svakog pravila koristeći MAM postupak: Ukoliko smo snagu ažurirali 1/β puta Fj = Fj + β(κj' - Fj). U suprotnom, Fj postaje srednja vrijednost trenutne i prethodne vrijednosti relativne preciznosti pravila „j“.
Naposljetku, najveća se vrijednost u nizu predviđanja umanjena za neki faktor koristi se za ažuriranje pravila iz prethodnog akcijskog skupa. Model XCS-a dan je na slici 3.4. Iako je XCS kompleksniji od ZCS-a, danas se većina klasifikatorskih sustava gradi upravo na XCS modelu. Više o samoj primjeni XCS-a i drugih klasifikatorskih sustava biti će riječi u sljedećem poglavlju.
vrh 5. Primjena LCS-aLCS se uglavnom upotrebljava za rješavanje jednog od ova četiri tipa problema: klasifikacijski problemi (classification problems), problemi učenja potkrjepljenjem (reinforcement learning problems), problemi aproksimacije funkcija (function approximation problems), problemi predviđanja (prediction problems) [11].
Klasifikacijski problemi predstavljaju probleme čiji je cilj raspoređivanje (klasificiranje) skupine objekata u podskupine (klase) i određivanje pravila po kojima se objekti raspoređuju. LCS koji se primjenjuje na klasifikacijske probleme nastoji pronaći takav skup pravila po kojima se klasificiranje obavlja što preciznije. Klasifikacijski problemi tipični su za područje dubinske analiza podataka (data mining).
Problemi učenja potkrjepljenjem svode se na pronalaženje optimalne funkcije ponašanja, a u LCS-u je ta funkcija predstavljena skupom pravila. Jedan od primjera problema učenja potkrjepljenjem je problem labirinta (maze problem). Cilj LCS-a koji se primjenjuje na problemima aproksimacije funkcije je što točnija aproksimacija funkcije skupom pravila koja se djelomično preklapaju. Primjer takvog problema je problem aproksimacije sinusne funkcije linearnim dijelovima [11].
LCS se može primijeniti u rješavanju gotovo svih problema predviđanja. Tako je LCS uspješno implementiran i u problemu predviđanja koordinacijskog broja amino kiseline u proteinskoj strukturi.
Od područja primjene LCS svakako treba spomenuti: dubinsku analizu podataka (data mining), upravljanje procesima i modeliranje i optimizaciju [3]. U tablici 3.1 su za spomenuta područja dani primjeri aplikacija koje upotrebljavaju LCS.
| Područja primjene LCS-a | Primjeri aplikacija |
| Dubinska analiza podataka | Klinička istraživanja: procjenjivanje opasnosti ozljede analizom podataka o preživljavanju te ozljede |
| Klasifikacija gljiva | |
| Upravljanje procesima | Kontrola protoka u plinskim cjevovodima |
| Kontrola signalizacije na prometnim raskrižjima | |
| Distribuirano usmjeravanje u komunikacijskim mrežama | |
| Modeliranje i optimizacija | Modeliranje ponašanja brokera |
| Navigacija robota |
- Eiben A. E., Smith J. E., Introduction to Evolution Computing, 1. izdanje, Berlin: Springer-Verlang, 2003.
- Sigaud O., Wilson S., Learning Classifier Systems: A Survey, dostupno na:
http://animatlab.lip6.fr/papers/sigaud_wilson_lcs_survey.pdf, listopad 2007. - Bull L., Learning Classifier Systems: A Brief Introduction, dostupno na:
http://www.cems.uwe.ac.uk/lcsg/introchap.pdf, listopad 2007. - Bernando-Mansilla E., Garrell-Guiu J. M., Accuracy-Based Learning Classifier Systems:
Models, Analysis and Applications to Classification Tasks, dostupno na:
http://sci2s.ugr.es/keel/pdf/keel/articulo/bernado03accuracy.pdf, listopad 2007. - Wikipedia: Machine learning, Reinforcement learning, Supervised learning, dostupno
na:
http://en.wikipedia.org/wiki/Machine_learning, studeni 2007. - Golub M., Genetski algoritam, rujan 2004., dostupno na:
http://www.zemris.fer.hr/~golub/ga/ga_skripta1.pdf, listopad 2007. - Kaelbling L. P., Littman M. L., Moore A. W., Reinforcement Learning: A Survey,
dostupno na:
http://www.cs.cmu.edu/afs/cs/project/jair/pub/volume4/kaelbling96a.pdf, studeni 2007. - Vasilyev A., Synergetic Approach in Adaptive Systems, magistarski rad, Transport
and Telecommunication Institute, Riga, 2002., dostupno na:
http://www.cs.rtu.lv/dssg/download/thesis/bimsc/2002/Vasilyev-MSc-2002-en.pdf, studeni 2007. - Weise T., Achler S., Gob M., Voigtmann C., Zapf M., Evolving Classifiers – Evolutionary
Algorithms in Data Mining, dostupno na:
https://kobra.bibliothek.uni-kassel.de/bitstream/urn:nbn:de:hebis:34-2007092819260/1
/Technicalreport2007_4.pdf, studeni 2007. - Beasley D., Q1.4: What's a Classifier system (CFS)?, svibanj 2007., dostupno na:
http://www.faqs.org/faqs/ai-faq/genetic/part2/section-5.html, listopad 2007. - Butz M. V., Learning Classifier Systems, dostupno na:
http://delivery.acm.org/10.1145/1280000/1274104/p3035-butz.pdf, listopad 2007. - Cordon O., del Jesus M. J., Herrera F., Evolutionary Approaches To The Learning
Of Fuzzy Rule–based Classification Systems, dostupno na:
http://sci2s.ugr.es/publications/ficheros/cordon-del_jesus-herrera-Evolutionary%20approaches-1999-107-160.pdf, studeni 2007. - Bacardit J., Krasnogor N., Introduction to Learning Classifier Systems, dostupno
na:
http://www.cs.nott.ac.uk/~nxk/TEACHING/G53BIO/LCS-1.ppt, studeni 2007. - Garrell-Guiu J. M., Pittsburgh Genetic-Based Machine Learning in the Data Mining
era: Representations, generalization, and run-time, doktorat, Universitat Ramon
Llull: Enginyera i Arquitectura La Salle, Barcelona, listopad 2004., dostupno na:
http://sci2s.ugr.es/keel/pdf/keel/tesis/bacardit.pdf, studeni 2007. - Kusiak A., Learning Classifier Systems: An Introduction, dostupno na:
http://www.icaen.uiowa.edu/~ie238/Lecture/LCS_2.pdf, studeni 2007.