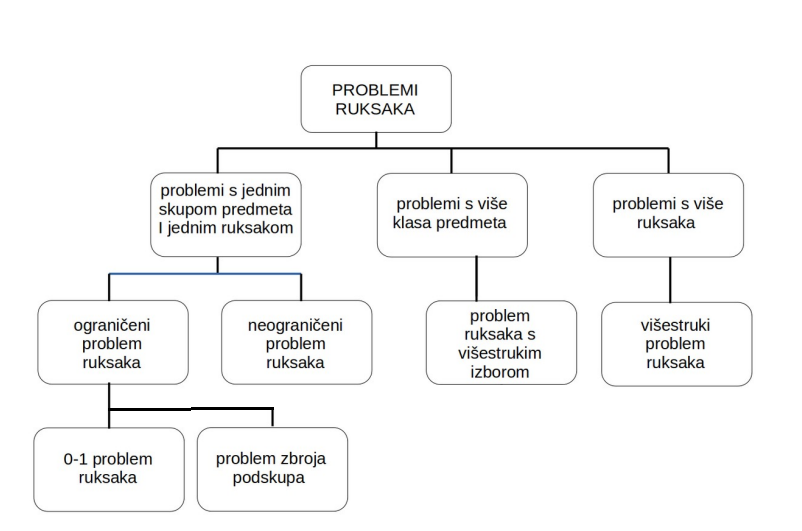
Problem ruksaka (eng. Knapsack Problem) jedan je od osnovnih optimizacijskih problema te, prema istraživanju iz 1999., jedan od najkorištenijih problema iz područja kombinatorne optimizacije. Ovaj problem, poznat i kao problem naprtnjače u hrvatskoj literaturi, jedan je od implementiranih problema u ovome projektu. U osnovi, problem ruksaka se svodi na pitanje kako odabrati određene predmete iz skupa predmeta tako da se maksimizira određeni ciljni kriterij, najčešće ukopna vrijednost, uz ograničenje na ukupnu težinu tih predmeta koja ne smije prelaziti zadani kapacitet ruksaka. Problemi ruksaka pojavljuju se u stvarnim procesima donošenja odluka u raznim područjima, kao što su pronalaženje najučinkovitijeg načina obrade sirovina, odabir investicija i portfolija, ali i u informatički sustavima pa je tako jedno od prvih rješenja za generiranje javnih ključeva za kriptosustave – Merkle-Hellman – koristilo problem ruksaka u svojoj formulaciji
U ovom radu, 0-1 problem ruksaka riješen je koristeći genetski algoritam. Ovaj klasični problem definira se nad skupom od n predmeta, gdje svaki predmet ima svoju težinu wi i vrijednost vi. Postoji također kapacitet ruksaka W, odnosno maksimalna težina koju ruksak može podnijeti.
Cilj je odabrati podskup predmeta kako bi se maksimizirala njihova ukupna vrijednost, ali bez prekoračenja kapaciteta ruksaka W. Rješenje se predstavlja karakterističnim vektorom [x1, x2, ..., xn], gdje varijabla xi za svaki predmet i označava je li predmet uključen u ruksak (xi = 1) ili nije (xi = 0).
Formalni zapis ove definicije dan je sljedećim izrazom:
Pohlepni algoritam je jednostavan pristup u kojem se predmeti biraju na temelju određenog kriterija, obično omjera vrijednosti i težine (vi/wi). Algoritam počinje praznim ruksakom i iterativno dodaje predmete koji daju najveći omjer. Ovaj pristup brzo daje rješenje, ali ne jamči optimalnost.
Ova se metoda temelji na principu razdvajanja problema na manje podprobleme. Algoritam gradi stablo odlučivanja i primjenjuje ograničenja kako bi izbjegao nepotrebne računske korake. Horowitz-Sahnijev algoritam i Martello-Tothov algoritam su specifične varijacije Branch-and-Bound metode koje su razvijene za rješavanje problema ruksaka.
Slično kao i branch-and-bound pristup, dinamičko programiranje podjeljuje problem na manje podprobleme i gradi tablicu (matricu) koja sadrži optimalna rješenja za svaki od tih podproblema. Poznati algoritmi koji su za problem ruksaka razvijeni na metodologiji dinamičkog programiranja su Tothov i Horowitz-Sahnijev algoritam.
Ovi algoritmi se koriste za transformaciju problema ruksaka u druge, manje složene probleme. Nakon transformacije, koristi se algoritam koji je razvijen za novi problem kako bi se pronašlo rješenje.
Ovi algoritmi se koriste za transformaciju problema ruksaka u druge, manje složene probleme. Nakon transformacije, koristi se algoritam koji je razvijen za novi problem kako bi se pronašlo rješenje.
Osim navedenih pristupa postoje i algoritmi, poput Balas-Zemelovog algoritma, Fayard-Plateauovog algoritma i Martello-Tothovog algoritma, posebno razvijeni za rješavanje velikih instanci problema ruksaka.
Problemi ruksaka mogu se generalizirati ili specijalizirati na razne načine, kao što su ograničenja na broj odabranih instanci ili uvođenje višestrukih ruksaka. Ove varijacije doprinose širokoj primjenjivosti problema u različitim područjima.
