Problemi optimizirani s GA
Knitting Problem
Problemi rezanja (knitting/cutting problem) predstavljaju ključni aspekt u raznim industrijama gdje se materijali, bez obzira na vrstu - bilo da se radi o metalima, staklu, drvu ili tkaninama, moraju prilagoditi specifičnim zahtjevima proizvodnje. Ovi zahtjevi mogu uključivati preciznost rezanja kako bi se postigla visoka kvaliteta proizvoda, minimiziranje gubitaka materijala kako bi se smanjili troškovi proizvodnje ili optimizaciju iskorištavanja resursa kako bi se povećala učinkovitost proizvodnje. Rješenja ovih problema mogu varirati od jednostavnih, kao što su rezanje dužih materijala u manje komade određene duljine, do izrazito složenih, gdje se materijali moraju rezati u različite oblike i veličine kako bi se zadovoljili specifični dizajnerski ili proizvodni zahtjevi. Ovi faktori zajedno čine optimizaciju problema rezanja izazovnim zadatkom. Stoga, kako bi se efikasno rješavali optimizacijski problemi rezanja, često se koriste različite računalne tehnike, pri čemu genetski algoritmi postaju sve popularniji izbor.
Podjela problema rezanja
- Problemi 1D rezanja: Problemi 1D rezanja odnose se na situacije u kojima je potrebno rezati jednodimenzionalne materijale na manje komade određene duljine. Ovi problemi često nastaju u industrijama gdje se materijali isporučuju u dužim trakama ili šipkama.
- Problemi 2D rezanja: Problemi 2D rezanja odnose se na rezanje dvodimenzionalnih materijala, kao što su listovi metala, stakla ili tkanine, na manje komade specifičnih dimenzija i oblika. Ovi problemi često prevladavaju u industrijama gdje se ravni materijali koriste za proizvodnju različitih proizvoda, kao što su prozorski okviri, pakiranje ili tekstil.
- Problemi 3D rezanja: Problemi 3D rezanja posebno su složeni jer se odnose na rezanje materijala u trodimenzionalne oblike. Ova vrsta problema često se primjenjuje u industrijama koje se bave obradom metala, plastike ili drugih materijala gdje su potrebni složeni oblici i detalji.
U ovom radu bavili smo se 2D problemom rezanja.
Optimizacijski ciljevi
Maksimizacija iskoristivosti
U nekim slučajevima, posebno u tekstilnoj industriji ili proizvodnji odjeće, glavni cilj može biti maksimizirati iskoristivost rezanih komada materijala. Ovaj pristup može biti ključan u situacijama gdje je svaki komad materijala vrjedniji od otpada koji se generira.Minimizacija troškova rezanja
Troškovi rezanja uključuju različite aspekte, uključujući troškove rada, troškove opreme i energije. Cilj u ovom slučaju može biti minimizirati ukupne troškove rezanja. Ovo zahtijeva uzimanje u obzir učinkovitosti procesa rezanja i brzine obrade materijala.Matematička formulacija
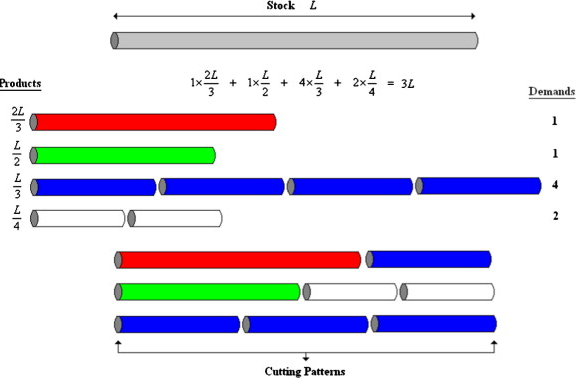
Standardna matematička formulacija za 1D problem rezanja (ali ne i jedina) počinje listom od m zahtijeva, od kojih svaki zahtjeva ni komada dužine li, gdje je koji trebaju biti izrezani iz zalihe (npr. šipke) veličine L. Zatim konstruiramo listu svih mogućih kombinacija rezova (često zvanih „uzorci“), pridružujući svakom uzorku pozitivnu varijablu xi koja predstavlja broj komada zaliha koje treba rezati pomoću uzorka j . Tada je linearni problem rezanja s cjelobrojnim rješenjima jednak:
\( \min \sum_{j} w_j x_j \quad\\\) takav da \( \quad\sum_{j} a_{ij}x_j = n_i, \quad \forall i = 1, \ldots, m, \quad \\x_j \geq 0 \text{ i cijeli broj} \)
Gdje je aij broj puta kada se zahtjev i pojavljuje u uzorku j, a wi je otpad uzorka j. Da bi elementi aij=1, ..., m činili izvedi uzorak rezanja, mora se zadovoljiti sljedeće ograničenje:
\( \sum_{i=1}^{m} a_{ij} \leq L, \\ \quad a_{ij} \geq 0 \text{ i cijeli broj.} \)
Primjer 1D rezanja šipke
