Numeričke metode rješavanja
diferencijalnih
jednadžbi
Eulerova metoda
Eulerova metoda je vrlo
popularna metoda za
rješavanje diferencijalnih jednadžbi, ali ima nedostatak
zbog velikih pogrešaka
prilikom zaokruživanja rezultata. Ova metoda je zasnovana na
korištenju
Taylorovog teorema reda 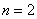 na intervalu na intervalu 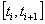 ,
gdje je ,
gdje je 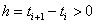 ,
te se za primjer diferencijalne jednadžbe prvog reda: ,
te se za primjer diferencijalne jednadžbe prvog reda:
može pisati:
|
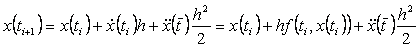 , ,
|
(13)
|
za neki 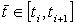 .
U ovom slučaju je .
U ovom slučaju je 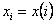 pravo
rješenje diferencijalne jednadžbe u trenutku pravo
rješenje diferencijalne jednadžbe u trenutku 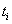 .
Ako iz jednadžbe (13) izbacimo
ostatak, dobivamo aproksimaciju točnog rješenja: .
Ako iz jednadžbe (13) izbacimo
ostatak, dobivamo aproksimaciju točnog rješenja:
Jednadžba (14)
predstavlja Eulerovu metodu.
Jednadžba za Eulerovu
metodu je nesimetrična,
što znači da nalazi rješenje za vremenski
interval 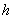 ,
ali pri tome koristi samo informacije o derivaciji s početka intervala
(slika
3). ,
ali pri tome koristi samo informacije o derivaciji s početka intervala
(slika
3).
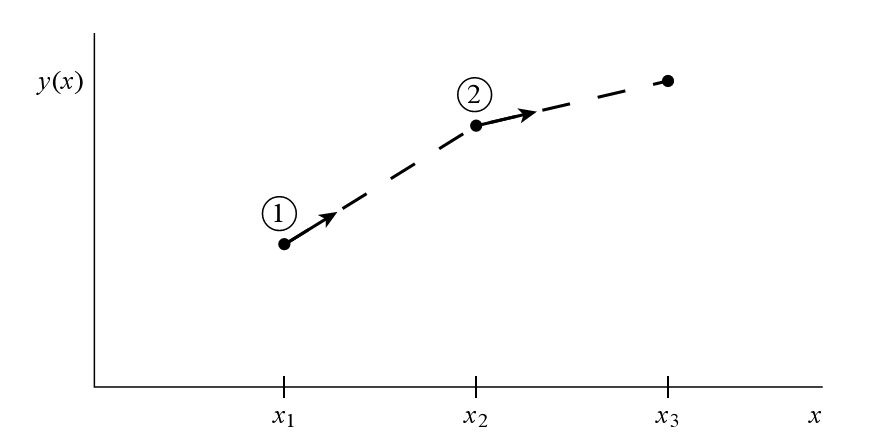
Slika 3. Eulerova
metoda za izračun
slijedeće vrijednosti funkcije koristi derivaciju na početku
intervala
Prilikom analize
kvalitete numeričke
metode bitno je odrediti najveću moguću vrijednost pogreške,
tj. vrijednosti 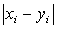 .
Činjenica je da se pogreška metode povećava s korakom .
Činjenica je da se pogreška metode povećava s korakom 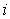 . .
Pošto
parcijalna derivacija po 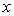 funkcije funkcije 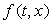 u
nekom četverokutu koji sadrži početnu točku u
nekom četverokutu koji sadrži početnu točku 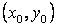 mora
biti kontinuirana, mora vrijediti i nejednakost: mora
biti kontinuirana, mora vrijediti i nejednakost:
|
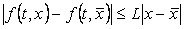
|
(15)
|
za neku konstantu 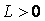 i
za svaki i
za svaki 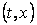 i i 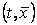 unutar
četverokuta domene. Uz pretpostavku da postoji unutar
četverokuta domene. Uz pretpostavku da postoji 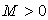 za
koji vrijedi za
koji vrijedi 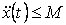 za
sve za
sve 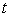 za
koje se traži rješenje diferencijalne jednadžbe, može se
odrediti gornja
vrijednost izraza za pogrešku. za
koje se traži rješenje diferencijalne jednadžbe, može se
odrediti gornja
vrijednost izraza za pogrešku.
|

|
(16)
|
Ako se definira 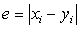 ,
tada nejednakost (16) prelazi u
oblik ,
tada nejednakost (16) prelazi u
oblik 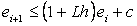 ,
za ,
za 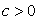 .
Početna greška je .
Početna greška je 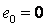 .
Greška pri koraku .
Greška pri koraku 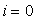 je: je:
|
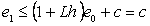
|
(17)
|
Greška pri
koraku 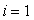 je: je:
|
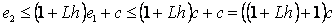
|
(18)
|
Greška pri
koraku 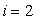 je: je:
|
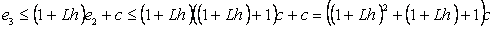
|
(19)
|
Općenito za 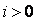 vrijedi: vrijedi:
|
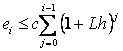
|
(20)
|
Koristeći činjenicu da je
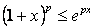 ,
za ,
za 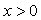 i i 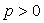 ,
te supstitucijom ,
te supstitucijom 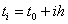 ,
može se gornja suma (20) dalje
raspisati: ,
može se gornja suma (20) dalje
raspisati:
|

|
(21)
|
gdje je krajnja granica 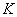 konstanta
koja sadrži konstanta
koja sadrži 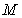 i i 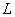 ,
te koristi činjenicu da je eksponencijalna funkcija omeđena na zadanom
intervalu ,
te koristi činjenicu da je eksponencijalna funkcija omeđena na zadanom
intervalu 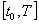 ,
tj ,
tj 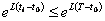 .
Izvod (21) je pokazao da je gornja granična vrijednost
pogreške ovisna o
konstanti .
Izvod (21) je pokazao da je gornja granična vrijednost
pogreške ovisna o
konstanti 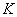 ,
te veličini koraka ,
te veličini koraka 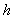 .
Može se zaključiti da će manji korak povećati preciznost daljnjeg
proračuna, ali će sukladno s time, zbog većeg broja potrebnih
iteracija da se dođe do krajnjeg .
Može se zaključiti da će manji korak povećati preciznost daljnjeg
proračuna, ali će sukladno s time, zbog većeg broja potrebnih
iteracija da se dođe do krajnjeg 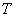 ,
i vrijeme računanja porasti, te se pri upotrebi algoritma mora naći
kompromis između preciznosti i vremena trajanja izračuna. ,
i vrijeme računanja porasti, te se pri upotrebi algoritma mora naći
kompromis između preciznosti i vremena trajanja izračuna.
Dosadašnja
analiza se zasnivala na
činjenici da greška u izračunu nastaje samo uslijed
zanemarivanja
članova višeg stupnja u aproksimaciji zadane funkcije
Taylorovim redom,
međutim grešku u proračun unosi i aritmetika brojeva s
pomičnim
zarezom implementirana u današnjim računalima. Zbog
nedostataka u
implementaciji aritmetike realnih brojeva u računalima, prilikom
izračuna vrijednosti 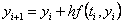 u
rezultantnu vrijednost se unosi sitna greška u
rezultantnu vrijednost se unosi sitna greška 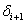 nastala
prilikom zaokruživanja brojeva s pomičnim zarezom. Rezultat dobiven
Eulerovom metodom priliko korištenja aritmetike brojeva s
pomičnim zarezom
može se prikazati kao: nastala
prilikom zaokruživanja brojeva s pomičnim zarezom. Rezultat dobiven
Eulerovom metodom priliko korištenja aritmetike brojeva s
pomičnim zarezom
može se prikazati kao:
|
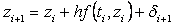
|
(22)
|
I u ovom slučaju izraz za
pogrešku se
prikaže na sličan način kao prije, te se dobiva:
|
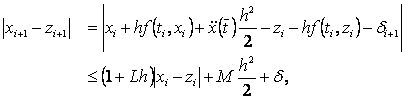
|
(23)
|
gdje je 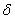 gornja
granica svih gornja
granica svih 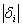 vrijednosti. vrijednosti.
Grešku u
iteraciji 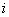 definiramo
kao: definiramo
kao: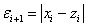 ,
ali se u ovom slučaju početna vrijednost pogreške ne može
uzeti kao ,
ali se u ovom slučaju početna vrijednost pogreške ne može
uzeti kao 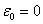 ,
jer nije sigurno da je početna vrijednost ,
jer nije sigurno da je početna vrijednost 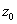 u
obliku broja s pomičnim zarezom potpuno jednaka vrijednosti u
obliku broja s pomičnim zarezom potpuno jednaka vrijednosti 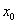 .
Za iteraciju .
Za iteraciju 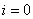 vrijedi: vrijedi:
|
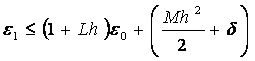
|
(24)
|
Za iteraciju 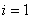 vrijedi: vrijedi:
|
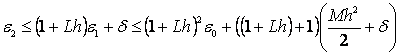
|
(25)
|
Za iteraciju 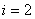 vrijedi: vrijedi:
|
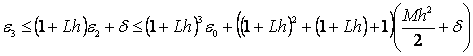
|
(26)
|
Uz 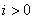 i
neke konstante i
neke konstante 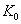 , , 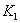 , , 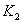 ,
općeniti oblik izraza za pogrešku je ,
općeniti oblik izraza za pogrešku je
|

|
(27)
|
Bitna stvar za uočiti u
gornjoj
nejednakosti je postojanje izraza 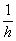 po
kojem se ova nejednakost razlikuje od izraza za gornju graničnu
grešku u
kojem nije u obzir uzeta pogreška prilikom rada s brojevima
s pomičnim
zarezom (21). Dok je prijašnji rezultat (21) ukazivao na
činjenicu da
se gornja granična greška smanjuje smanjenjem intervala po
kojem se ova nejednakost razlikuje od izraza za gornju graničnu
grešku u
kojem nije u obzir uzeta pogreška prilikom rada s brojevima
s pomičnim
zarezom (21). Dok je prijašnji rezultat (21) ukazivao na
činjenicu da
se gornja granična greška smanjuje smanjenjem intervala 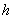 ,
izvod (27) ukazuje na mogućnost povećanja gornje granične
pogreške do beskonačnosti u slučaju smanjenja intervala ,
izvod (27) ukazuje na mogućnost povećanja gornje granične
pogreške do beskonačnosti u slučaju smanjenja intervala 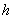 na
nulu. Da bi se postigla najmanja vrijednost pogreške
potrebno je odabrati
vrijednost na
nulu. Da bi se postigla najmanja vrijednost pogreške
potrebno je odabrati
vrijednost 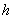 takvu
da je funkcija takvu
da je funkcija 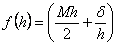 u
svom globalnom minimumu, što je zadovoljeno za u
svom globalnom minimumu, što je zadovoljeno za 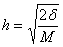 . .
Runge-Kutta metode
Runge-Kutta metode su
zamišljene da imaju
aproksimacijske greške višeg stupnja, ali i da za
njih nije potrebno
računati parcijalne derivacije funkcije 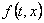 ,
što je u fizikalnim simulacijama neizvedivo, zbog toga
što se unaprijed ne zna
buduće stanje sustava. ,
što je u fizikalnim simulacijama neizvedivo, zbog toga
što se unaprijed ne zna
buduće stanje sustava.
Za izvod Runge-Kuta
metoda potrebno je
proširiti Taylorov teorem na funkciju s dvije varijable.
Neka su funkcija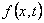 i njene parcijalne derivacije do uključujući stupnja
i njene parcijalne derivacije do uključujući stupnja 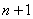 kontinuirane
na domeni kontinuirane
na domeni 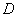 .
Neka je .
Neka je 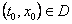 .
Za svaki .
Za svaki 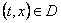 postoje postoje 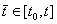 i i
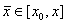 takvi
da vrijedi takvi
da vrijedi 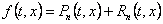 ,
gdje je ,
gdje je 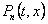 Taylorov
polinom stupnja Taylorov
polinom stupnja 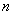 : :
|
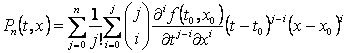 , ,
|
(33)
|
a 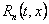 ostatak
razvoja u Taylorov red: ostatak
razvoja u Taylorov red:
|
 . .
|
(34)
|
Metode drugog stupnja
Primjena Taylorovog
teorema na rezultat 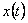 dovodi
do jednadžbe dovodi
do jednadžbe 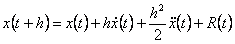 ,
gdje je ,
gdje je 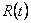 ostatak
stupnja ostatak
stupnja 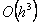 .
Koristeći jednakosti .
Koristeći jednakosti 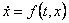 i i  dobiva
se: dobiva
se:
|
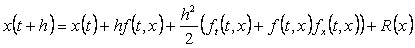 . .
|
(35)
|
Za računanje gornjeg
izraza je potrebno
znati parcijalne derivacije prvoga reda funkcije 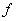 ,
što se želi izbjeći primjenom ove metode. Novom
aproksimacijom se mogu zamijeniti
derivacije funkcije ,
što se želi izbjeći primjenom ove metode. Novom
aproksimacijom se mogu zamijeniti
derivacije funkcije 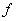 s
njenom trenutnom vrijednošću, tj. želi se dobiti izraz u
obliku s
njenom trenutnom vrijednošću, tj. želi se dobiti izraz u
obliku
|
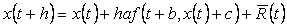 , ,
|
(36)
|
za neke 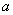 , ,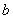 , ,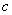 ,
te ostatke ,
te ostatke 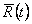 stupnja stupnja 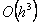 .
Korištenjem Taylorovog teorema za funkcije dvije varijable
dobiva se: .
Korištenjem Taylorovog teorema za funkcije dvije varijable
dobiva se:
|
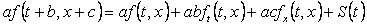 , ,
|
(37)
|
gdje je 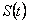 stupnja stupnja
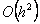 .
Desna strana jednadžbe (36) uz
uvrštenje gornje jednakosti ima isti oblik kao jednadžba
(34), pa se mogu odrediti koeficijenti .
Desna strana jednadžbe (36) uz
uvrštenje gornje jednakosti ima isti oblik kao jednadžba
(34), pa se mogu odrediti koeficijenti 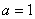 , ,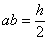 i
i 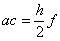 ,
a izraz za grešku je ,
a izraz za grešku je 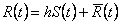 .
Uvrštenjem .
Uvrštenjem 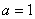 , ,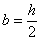 i
i 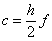 u
jednadžbu (36) dobiva se: u
jednadžbu (36) dobiva se:
|
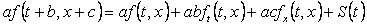 . .
|
(38)
|
Iz gornje jednadžbe se
dobiva numerička
metoda nazvana metoda srednje točke (eng. midpoint method):
|
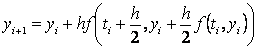 . .
|
(39)
|
Metoda srednje točke je
nastala kao
rezultat korištenja Taylorovog polinoma stupnja 1 da se
aproksimira 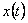 ,
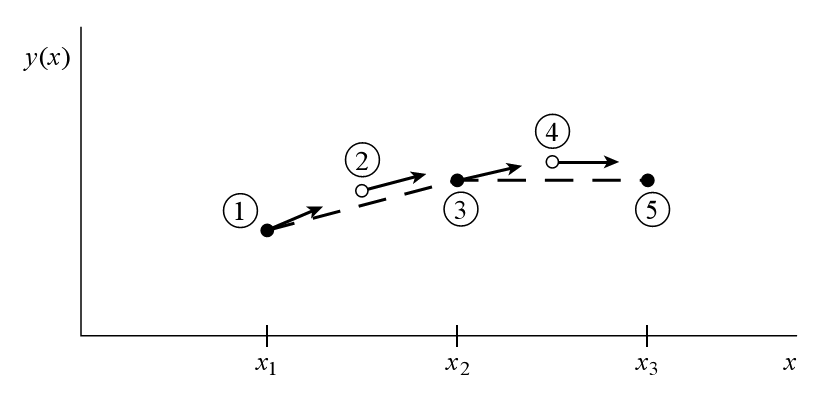
te numerička metoda ima grešku stupnja ,
te numerička metoda ima grešku stupnja 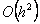 .
Kod ove metode se derivacija na početku intervala koristi da bi se
našla
derivacija na sredini intervala. Nakon toga se ta vrijednost derivacije
koristi
kao derivacija za izračun funkcije na kraju intervala. .
Kod ove metode se derivacija na početku intervala koristi da bi se
našla
derivacija na sredini intervala. Nakon toga se ta vrijednost derivacije
koristi
kao derivacija za izračun funkcije na kraju intervala.
Slika 4. Metoda
srednje
točke
Moglo bi se pomisliti da
bi se istim
načinom, ali korištenjem Taylorovog polinoma stupnja 2 mogla
postići
greška stupnja 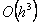 ,
međutim ovaj način konstruiranja numeričke metode može dovesti
jedino do metoda s greškama stupnja ,
međutim ovaj način konstruiranja numeričke metode može dovesti
jedino do metoda s greškama stupnja 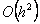 .
Razvoj Taylorovog reda stupnja 2 daje: .
Razvoj Taylorovog reda stupnja 2 daje:
|

|
(40)
|
gdje je 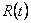 stupnja stupnja
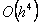 .
Da se zamjene izrazi derivacija funkcije s vrijednostima funkcije
koristi se
izraz: .
Da se zamjene izrazi derivacija funkcije s vrijednostima funkcije
koristi se
izraz:
|
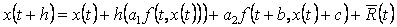 , ,
|
(41)
|
uz neke koeficijente 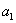 , ,
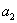 , , 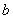 i i 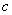 ,
te ostatak ,
te ostatak 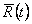 stupnja stupnja 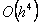 .
Koristeći Taylorov teorem prošire se izrazi koji uključuju
funkciju .
Koristeći Taylorov teorem prošire se izrazi koji uključuju
funkciju 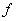 : :
|
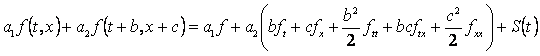 , ,
|
(42)
|
gdje je 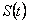 stupnja stupnja
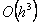 .
Izrazi (40) i (41), uz uvrštenu gornju jednakost (42),
skoro odgovaraju, osim elementa .
Izrazi (40) i (41), uz uvrštenu gornju jednakost (42),
skoro odgovaraju, osim elementa 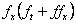 .
Ako se ti izrazi pokušaju izjednačiti i izračunati
odgovarajući
koeficijenti, može se odrediti .
Ako se ti izrazi pokušaju izjednačiti i izračunati
odgovarajući
koeficijenti, može se odrediti 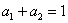 , , 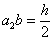 i i
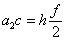 uz
izraze uz
izraze 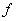 , ,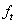 i
i 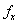 .
Svi ostali izrazi iz jednadžbe (40) moraju postati dio ostatka .
Svi ostali izrazi iz jednadžbe (40) moraju postati dio ostatka 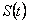 ,
čiji stupanj se time smanjuje na ,
čiji stupanj se time smanjuje na 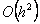 .
Iz tri dobivene jednadžbe postoji više različitih
rješenja za
koeficijente. Jedno od rješenja može biti: .
Iz tri dobivene jednadžbe postoji više različitih
rješenja za
koeficijente. Jedno od rješenja može biti: 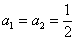 , ,
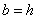 i i 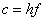 .
Time se dobiva numerička metoda poznata pod nazivom modificirana
Eulerova
metoda: .
Time se dobiva numerička metoda poznata pod nazivom modificirana
Eulerova
metoda:
|
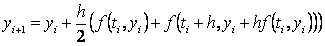 . .
|
(43)
|
Druga metoda je poznata
pod nazivom Heunova
metoda. Dobije se za rješenja jednadžbi 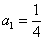 , ,
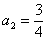 , , 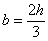 i i 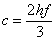 i
glasi: i
glasi:
|
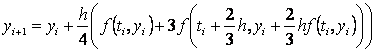 . .
|
(44)
|
Metode trećeg stupnja
Ako se prilikom zamjene
izraza derivacije
funkcije s vrijednostima funkcije umjesto jednostruko ugniježđene
funkcije 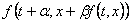 koristi
dvostruko ugniježđena funkcija koristi
dvostruko ugniježđena funkcija
|
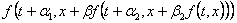 , ,
|
(45)
|
tada se mogu podudarati i
izrazi višeg
stupnja. Da bi se dobila Runge-Kutta numerička metoda trećeg stupnja
potrebno je proširiti gornji izraz korištenjem
Taylorovog teorema. To se
postiže tako da se prvo proširi izraz 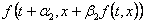 .
Rezultat se supstituira u ukupni izraz, te se takav proširi
upotrebom
Taylorovog teorema. .
Rezultat se supstituira u ukupni izraz, te se takav proširi
upotrebom
Taylorovog teorema.
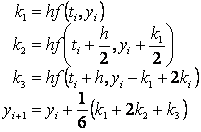
Jedna od metoda koja se
dobije takvim
postupkom je:
|
|
(46)
|
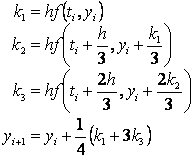
Dok je druga:
|
|
(47)
|
Metode četvrtog stupnja
Izvod Runge-Kutta
numeričke metode
četvrtog stupnja kreće od aproksimacije funkcije 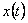 po
Taylorovom teoremu: po
Taylorovom teoremu:
|
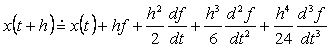
|
(48)
|
Zamjena izraza derivacija
funkcije s
vrijednostima same funkcije se provodi kao u prethodnim slučajevima,
ali
će ovdje postojati po jedan izraz bez ugnježđivanja, te po jedan
izraz s jednostrukim, dvostrukim, te trostrukim ugnježđivanjem. Krajnji
stupanj izraza za pogrešku će biti 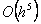 . .
Jedna od rezultirajućih
metoda je:
|

|
(49)
|
Među češće
korištenim metodama
je:
|
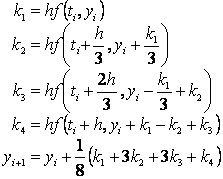
|
(50)
|
i Gillova metoda:
|

|
(51)
|
Na slici 5 je prikazan
način izračuna
vrijednosti funkcije korištenjem Runge-Kutta metode četvrtog
stupnja. Pri
izračunu svakog koraka gleda se derivacija četiri puta: jedan put u
početnoj točci, dva puta u ispitnoj srednjoj točci, te jedan put
u ispitnoj krajnjoj točci. Za svaku od tih vrijednosti se računa
krajnja vrijednost funkcije označena praznim krugovima, te se
korištenjem
tih rezultata dobije konačno rješenje označeno punim krugom.

Slika 5. Runge-Kutta metoda
četvrtog
stupnja
|
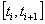 ,
gdje je
,
gdje je 

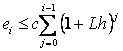

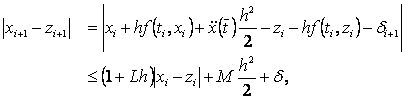
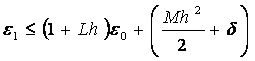
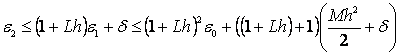
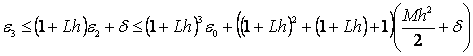

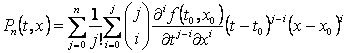 ,
, .
.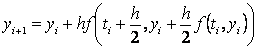 .
.

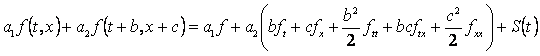 ,
,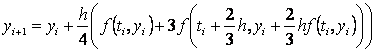 .
.




