Animacija fluida u okruženju s preprekama
| Uvod |
| Modeliranje |
| Matematicka formulacija |
| Algoritam SIMPLE |
| Diskretizacija |
| Implementacija |
| Rezultati |
| Download |
Diskretizacija Navier Stokesovih jednadžbi
Diferencijalni zapisNavier-Stokesovih jednadžbi sadrži različite oblike i stupnjeve derivacija tlaka i brzina. S lijeva na desno članovi su derivacija brzine po vremenu, brzine po prostoru, tlaka po prostoru i na kraju druga derivacija brzine po prostoru. Prvo je najjednostavnije:
![]()
gdje oznaka n označava vremenski korak. Kako je vrijeme diskretizirano u trenucima T+kΔt, keN, derivacija se svodi na jednostavnu promjenu vrijednosti u uzastopnim vremenskim koracima.
Derivacija tlaka po prostoru, s obzirom da je tlak definiran u središtima elemenata mreže, identična je općoj metodi diskretizacije prve derivacije
![]()
![]()
Prva derivacija same brzine rezultate daje točno u središtima elemenata, što je nepovoljno. Međutim, jedina alternativa je umjetno smanjenje rezolucije mreže, što je još gore rješenje. Prva derivacija brzine je zato:
![]()
![]()
Druga derivacija brzine će davati rezultat relevantan za traženu točku:
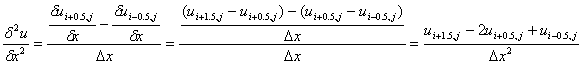
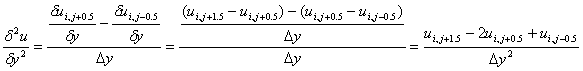
U ovom trenutku su definirane samo derivacije brzina u smjerovima na koje se odnose. Definirana je dakle samo prva i druga derivacija x komponente brzine po x-u i derivacije y komponente po y-u. Da bi se Navier Stokesove jednadžbe mogle ispisati u diskretnom obliku, potrebno je još dati objašnjenje derivacija brzina u suprotnim smjerovima.
Kako su brzine u x smjeru definirane u točkama (i+(2k+1)/2, j+k), keN, njihova prva derivacija u y smjeru neće iskoristiti prednosti posmaknute mreže iz jednostavnog razloga što x mreža nije posmaknuta u y smjeru. Zbog toga će ova vrijednost biti važeća za točku točno između dva dijagonalno postavljena glavna čvora. Slično razmatranje vrijedi i za y komponentu brzine. Prve derivacije će tako biti:
![]()
![]()
Derivacije drugoga stupnja će davati vrijednosti koje su važeće točno za čvorove mreža brzina koje se deriviraju.
![]()
![]()
U ovom trenutku su u diskretnom obliku definirani svi članovi Navier Stokesovih jednadžbi. Prije krajnje formulacije zanimljivo je pogledati koje vrijednosti tlakova i brzina su potrebne za rješavanje momentne jednadžbe za jedan čvor mreže, dakle za računanje iznosa brzina u x i y smjeru.
Na slici su plavim, crvenim i zelenim krugovima prikazani redom čvorovi tlaka, brzine u x smjeru i brzine u y smjeru. Lako se može primijetiti posmaknutost mreža. Žutom podlogom je označen element koji se obrađuje. Vidljivo je da je za rješavanje momentne jednadžbe za samo jednu diskretnu točku potrebno koristiti čak trinaest različitih vrijednosti. Iako se ovo može pročitati iz jednadžbi, na ovakvoj slici je lakše uočiti koliko su udaljene neke vrijednosti nužne za točan izračun. Pri implementaciji algoritma treba posebno paziti na elemente blizu rubova simuliranoga prostora ili blizu prepreka. Poseban oprez je potreban pri radu s tankim preprekama, širine jednoga elementa mreže, jer tada druga derivacija brzina može iskoristiti vrijednosti iz udaljenih čvorova koje mogu biti
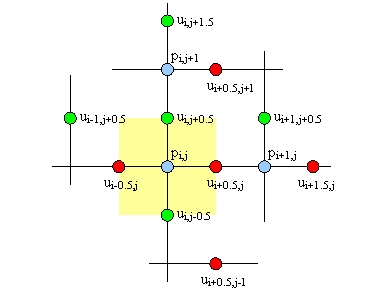
prilagođene uvjetima s druge strane prepreke.
Na kraju, Navier Stokesove jednadžbe, ili momentna jednadžba, u diskretnom i nevektorskom obliku glasi:
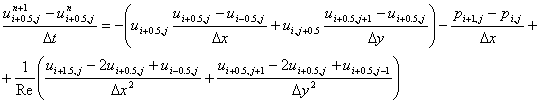
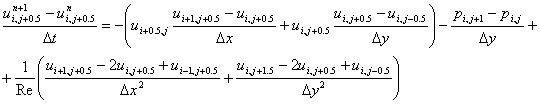
Diskretizacija Poissonove jednadžbe
Nakon gornjega pregleda diskretizacije derivacija, za Poissonovu jednadžbu su već dati gotovo svi potrebni izrazi. Jedino što je ostalo nedefinirano, pošto se ne koristi u momentnoj jednadžbi, je derivacija tlaka drugoga stupnja. Izraz glasi:
![]()
![]()
Diskretni oblik Poissonove jednadžbe je skalarni izraz s obzirom da je tlak skalarna veličina, pa tako ova jedna jednadžba glasi:
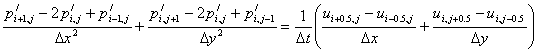
Izlučivanjem p'i,j iz gornje jednadžbe dobije se eksplicitni izraz za korekciju tlaka u točki (i, j). S obzirom da se susjedne korekcije dobijaju korištenjem jednake jednadžbe, proces računanja svih korekcija na mreži mora, kako je već pojašnjeno, biti iterativan.
Poissonova jednadžba u odnosu na momentnu jednadžbu donosi nove dvije vrijednosti potrebne za dovršetak jedne iteracije glavnog algoritma. Na slici je prikazana konačna slika potrebnih točki. Nove dvije vrijednosti su označene crnim krugom. To su vrijednosti čvorova tlaka koje nisu bile potrebne u momentnoj jednadžbi koja koristi samo prvu derivaciju tlaka, ali su potrebne u Poissonovoj gdje se koristi i druga derivacija. Za razliku od momentne jednadžbe, Poissonova ne koristi derivacije brzina drugoga stupnja, kao ni derivacije brzina po smjerovima kojima same ne pripadaju, pa su tako za rješenje ove jednadžbe dovoljne samo veličine koje omeđuju promatrani element, kao i vrijednosti tlakova u svim susjednim elementima.
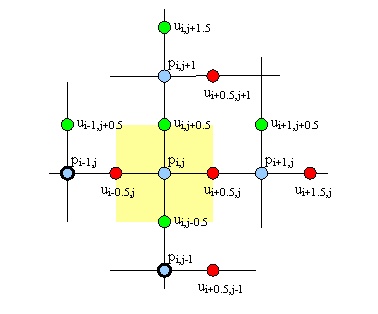
Za kompletno rješenje momentne i Poissonove jednadžbe za svaki element potrebno je koristiti ukupno petnaest vrijednosti tlaka i brzina. Iz ovoga je očito kolika je međusobna povezanost susjednih elemenata, a time i cjelokupne mreže elemenata. Iterativni se postupak, međutim, dobro nosi s ovim zadatkom.