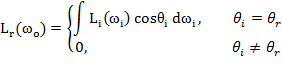Diplomski rad br. 5

U prethodnom poglavlju predstavljeni su različiti fizikalni modeli svjetla. Za potrebe računalne grafike (posebice u stvarnom vremenu), pojave koje je moguće prikazati valno-čestičnim modelom svjetlosti su zanemarive, budući da se događaju u rijetkim slučajevima, a znatno pridonose kompleksnosti problema. Iz tog razloga, u pravilu se pretpostavlja geometrijski model svjetla kao idealni, fotorealistični model. No, i takav ograničeni model potrebno je aproksimirati i pretočiti u oblik pogodan za računalnu implementaciju. Tradicionalno, u interaktivnoj računalnoj grafici promatra se samo direktni doprinos izvora svjetla na danu površinu. Drugim riječima, efekti poput difuzne interrefleksije ili ispodpovršinskog raspršivanja se zanemaruju, budući da se time problem izračuna osvjetljenja daleko pojednostavljuje (i u smislu jednostavnosti implementacije, i, još važnije, u smislu računalne zahtjevnosti). Dakle, potrebno je formulirati model koji opisuje osvijetljenost neke površine, u ovisnosti o intenzitetu i kutu upadne i reflektirane zrake svjetlosti. U općem slučaju, definira se funkcija koja opisuje reflektivnost površine. U literaturi, takva se funkcija naziva bidirekcionalna funkcija distribucije reflektivnosti (eng. bidirectional reflectance distribution function, BRDF). Formalno, opći oblik BRDF funkcije izgleda ovako:

Pritom je ω_i vektor upadne zrake svjetlosti, a ω_o vektor reflektirane zrake svjetlosti, dok je θ_i kut između vektora upadne zrake svjetlosti i normale na površinu u točki upada. Dakako, svi su spomenuti vektori jedinični. Iz tog razloga, mogu se parametrizirati dvjema sfernim koordinatama, kutom azimuta φ i kutom elevacije θ, dok je radijus po definiciji jednak jedan (iz ovoga slijedi da je konačna funkcija zapravo četverodimenzionalna). Nadalje, L_r je intenzitet reflektiranog svjetla (zračenje po steradijanu po jedinici površine, eng. radiance), dok je E_i upadno zračenje po steradijanu (eng. irradiance).  Dakle, BRDF funkcija za dani par upadnog i reflektiranog vektora definira odnos intenziteta reflektiranog svjetla i upadnog zračenja po steradijanu.

Na temelju općeg oblika BRDF funkcije, razvijeno je nekoliko različitih, konkretnih modela osvjetljenja koji se koriste u računalnoj grafici. Takvi modeli se dijele u dvije glavne skupine: analitički modeli (temelje se na aproksimacijama općeg oblika BRDF-a, pretpostavljajući određene parametre ili ograničenja, ili na heurističkim i numeričkim aproksimacijama), te empirijski modeli (zasnivaju se na mjerenjima reflektivnosti stvarnih materijala u laboratorijskim uvjetima).

Najjednostavniji analitički BRDF model može se izvesti pretpostavljajući direkcionalni izvor svjetlosti, te idealno difuznu površinu koja je ravna ploha. Kod direkcionalnog svjetla, upadne zrake svjetlosti su paralelne, te u ovom slučaju, sve upadaju pod istim kutem na površinu (normala na površinu je u svakoj točki upada jednaka). Također, budući da je površina savršeno difuzna, svaka upadna zraka se reflektira jednoliko u svim smjerovima, u hemisferi nad površinom. Uz navedene pretpostavke, BRDF funkcija se reducira na konstantnu vrijednost. Naime, kako je rečeno, vrijednost BRDF funkcije je omjer intenziteta reflektiranog svjetla i upadnog zračenja po steradijanu. Budući da se upadne zrake svjetlosti reflektiraju jednoliko po cijeloj hemisferi, bez obzira na kut upada ili poziciju promatrača, to znači da je traženi omjer jednak za bilo koji par upadnog i reflektiranog vektora zrake svjetlosti. Dakako, iz iskustva već znamo da intenzitet svjetlosti (zračenje po steradijanu po jedinici površine) opada s povećanjem upadnog kuta, a to je upravo zato što se jednak iznos zračenja rasprostire po većoj površini, pa intenzitet svjetlosti opada. Bez gubitka općenitosti, možemo uzeti da je navedeni omjer točno jednak jedan, pa dobivamo sljedeće:

S obzirom da L_i, L_r i θ_i više nisu funkcije upadnog ili reflektiranog vektora, ili normale na površinu, već konstante, možemo pisati:

Budući da je vektor ω_i parametriziran sfernim koordinatama (θ, φ) uz konstantan radijus, gornji integral zapravo opisuje površinu jedinične hemisfere, za koju možemo uzeti da je jednaka nekoj konstanti C, iz čega slijedi da je intenzitet reflektiranog svjetla proporcionalan intenzitetu upadnog svjetla pomnoženom s kosinusom upadnog kuta:

Valja primijetiti da smo ovim putem zapravo izveli Lambertov kosinusni zakon, koji predstavlja model difuzne refleksije tradicionalno korišten u računalnoj grafici, a čiji je standardni oblik:

gdje je I_d intenzitet difuznog osvjetljenja, i_d intenzitet difuzne komponente upadnog svjetla, L vektor upadne zrake svjetla, N vektor normale na površinu u točki upada, a k_d vrijednost iz intervala [0, 1] koja definira stupanj difuzne reflektivnosti površine (gdje k_d = 1 predstavlja idealno difuzni materijal).

Međutim, jasno je da je dobiveni model tek jedan specijalni slučaj, koji vrijedi samo ako su zadovoljene početne (vrlo ograničavajuće!) pretpostavke. Primjerice, za mnoge stvarne materijale ne vrijedi pretpostavka da je omjer intenziteta reflektiranog svjetla i upadnog zračenja po steradijanu jednak za svaki par upadnog i reflektiranog vektora zrake svjetlosti. Štoviše, kod idealnih ravnih zrcala, taj omjer je jednak nuli za sve takve parove vektora, osim za slučaj kada je upadni kut točno jednak kutu refleksije, kada je spomenuti omjer jednak jedan (gdje je upadni kut definiran kao kut između upadnog vektora i normale na površinu u točki upada, a kut refleksije kao kut između reflektiranog vektora i normale). Drugim riječima, idealna zrcala reflektiraju upadnu svjetlost u samo jednom, točno određenom smjeru, što rezultira neizobličenom, simetričnom slikom. Prema tome, BRDF funkcija se za idealna ravna zrcala može zapisati u sljedećem obliku:

Odnosno,

S druge strane, brojni materijali pokazuju nesavršenu zrcalnu reflektivnost, što znači da BRDF funkcija nije binarna, već može poprimiti bilo koji realni broj u intervalu [0, 1]. Kod nesavršeno zrcalnih objekata proizvoljnog oblika, dolazi do pojave zrcalnog odsjaja (eng. specular highlight), budući da se upadna svjetlost reflektira u  uskom stošcu oko idealno reflektirane zrake. Dakle, svo upadno zračenje će biti reflektirano na uskom dijelu površine, što znači da će to područje imati znatno veći intenzitet osvjetljenja, a otuda i naziv pojave. Širina zrcalnog odsjaja ovisi, dakako, o karakteristikama specifičnog materijala. Formalno, opisani se problem može zapisati na sljedeći način:

gdje je δ kut između vektora ω_o  i idealno reflektirane zrake (valja imati na umu da za zrcala koja nisu ravna, smjer idealno reflektirane zrake općenito ovisi o položaju promatrača), a f_s(δ) funkcija koja definira širinu zrcalnog odsjaja (dakle, opada s porastom δ).

Analitičko rješenje gornjeg izraza bi zahtijevalo izračunavanje integrala po hemisferi za svaki slikovni element, pri svakom osvježavanju slike, što nije primjenjivo za potrebe interaktivne računalne grafike. Iz tog razloga, svi postojeći modeli zrcalnog odsjaja se baziraju na određenim heuristikama i opažanjima. Primjerice, vjerojatno najpoznatiji je Phongov model, koji se bazira na opažanju da funkcija intenziteta odsjaja odgovara eksponencijalnoj:

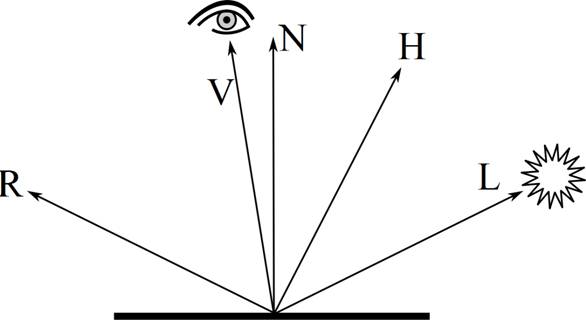
gdje je I_s intenzitet zrcalnog odsjaja, i_s intenzitet zrcalne komponente upadnog svjetla, R vektor idealno reflektirane zrake svjetla, V vektor promatrača, α faktor sjajnosti (određuje širinu i intenzitet zrcalnog odsjaja), a k_s vrijednost iz intervala [0, 1] koja definira stupanj zrcalne reflektivnosti površine (gdje k_s = 1 predstavlja idealno zrcalni materijal).

U praktičnim primjenama, pokazalo se da Phongov model pruža prihvatljivu aproksimaciju zrcalnog odsjaja, uz nisku računalnu složenost. No, češće se koristi varijanta nazvana Blinn-Phong model, koja u formuli (4) zamjenjuje izraz R·V izrazom N·H, gdje je N vektor normale na površinu, a H je tzv. poluvektor:

Poluvektor H se definira na sljedeći način:

Dakle, kao što je ilustrirano na slici 6, poluvektor H se nalazi "na pola puta" između vektora promatrača V, i vektora zrake svjetlosti L, pa otuda i naziv. Rezultati koji se dobiju Blinn-Phong modelom su vrlo slični rezultatima običnog Phong modela, iako se mogu primijetiti razlike u obliku zrcalnog odsjaja. Također, bitno je uočiti da skalarni umnožak R·V odgovara kosinusu kuta koji je dvostruko veći od kuta čijem kosinusu odgovara skalarni umnožak N·H, iz čega možemo zaključiti da bismo za dobivanje približno jednakih rezultata trebali prilagoditi eksponent α. Na slici 7 mogu se vidjeti zrcalne komponente osvjetljenja dobivene Blinn-Phong i Phong modelima. Prva slika slijeva prikazuje objekt osvijetljen Phong modelom, dok slika u sredini prikazuje isti objekt osvijetljen Blinn-Phong modelom uz identične parametre. Jasno je primjetljiv pojačan intenzitet i drugačiji oblik zrcalnog odsjaja. Uz prilagodbu eksponenta α, moguće je ostvariti odsjaj vrlo sličnog ili gotovo jednakog intenziteta, kako pokazuje zadnja slika slijeva - no, i dalje se mogu primijetiti suptilne razlike u obliku odsjaja.

Zanimljivo je istaknuti kako Blinn-Phong model, premda je nastao kao aproksimacija Phong modela, zapravo daje rezultate koji su bliži empirijski utvrđenim BRDF modelima, za brojne vrste stvarnih materijala. Ova kombinacija dobrih svojstava (rezultati vjerni stvarnima, niska računalna zahtjevnost) rezultirala je iznimnom popularnošću Blinn-Phong modela, te su rani grafički akceleratori, koji nisu pružali mogućnost programirljivih cjevovoda, sklopovski implementirali upravo Blinn-Phong model. Dakako, moderne programirljive grafičke kartice omogućuju implementaciju proizvoljnog modela osvjetljenja. Za specifične primjene, razvijeni su različiti, računalno zahtjevniji modeli koji pružaju rezultate vjernije stvarnosti, primjerice, u slučaju iscrtavanja ljudskih lica (kože), ili raznih drugih specifičnih materijala.