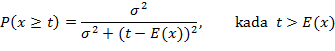Diplomski rad br. 5

Pitanje koje je dosad ostalo neodgovoreno, a koje ćemo razmotriti u ovom poglavlju, jest pitanje sjena. Naime, iz iskustva je već poznato da osvijetljeni objekti zaklanjaju određeni dio prostora, tako da taj prostor leži u sjeni. Međutim, opisanim postupcima osvjetljenja, računali bismo osvjetljenje i u prostoru koji bi trebao ležati u sjeni. Potreban je, dakle, poseban postupak kojim ćemo odrediti zaklonjenost. U tu svrhu, postoje dva glavna algoritma, od kojih svaki ima određene prednosti i nedostatke, a to su algoritam volumena sjene (eng. shadow volume), te algoritam preslikavanja sjena (eng. shadow mapping).

Algoritam volumena sjene se zasniva na ideji da se zaklonjeni prostor također može geometrijski opisati, kao i pravi objekti na sceni. Prema tome, scena se dijeli na dva dijela - početna geometrija scene, te geometrija sjena. Tu dodatnu geometriju, koju možemo nazvati volumen sjene (otuda i naziv algoritma) je potrebno generirati za svaki osvijetljeni objekt, za svako svjetlo zasebno. Postupak generiranja volumena sjene se sastoji od dva koraka: pronalaženje siluete objekta, te ekstruzije siluete u volumen. Silueta se definira kao skup bridova koji povezuju prednje i stražnje poligone objekta. Prednji poligoni su oni koji su orijentirani prema izvoru svjetla, a stražnji oni koji su orijentirani u suprotnom smjeru. Jednostavan test za određivanje koji poligoni su prednji, a koji stražnji, jest izračun skalarnog umnoška vektora normale poligona, te vektora smjera svjetla. Ukoliko je rezultat pozitivan broj, poligon je prednji, inače je stražnji. Jednom kad je određena silueta objekta, potrebno ju je proširiti u volumen, na način da se svakom vrhu siluete pridoda i bridom poveže novi vrh, pomaknut u smjeru suprotnom smjeru svjetla za dani vrh, i to na neku (beskonačno) veliku udaljenost. Opisani postupak predočava slika 13.

Konačno, sam postupak iscrtavanja scene sastoji se od sljedećih koraka:

1.      Iscrtaj scenu u spremnik okvira, kao da je u potpunosti u sjeni

2.      Generiraj volumene sjene

3.      Za svako svjetlo, čini sljedeće:

3.1.   Iscrtaj volumene sjene u spremnik šablone

3.2.   Iscrtaj scenu s osvjetljenjem, primjenjujući dobivenu masku

3.3.   Dodaj dobiveno osvjetljenje u spremnik okvira, aditivnim miješanjem

Prednost ovog postupka je što su sjene vrlo točne i precizne, bez obzira na poziciju kamere ili kut gledanja. Dapače, sjene mogu čak izgledati i preoštro, tj. neprirodno, stoga je moguće koristiti zamućivanje. Glavni nedostatak je potreba za generiranjem i iscrtavanjem dodatne geometrije sjena. Tradicionalno, određivanje silueta i proširivanje u volumene se vršilo na glavnom procesoru, no moderne grafičke kartice (DirectX 10 ili novije), nude mogućnost pisanja programa za sjenčanje geometrije (eng. geometry shader), a koji omogućuju generiranje volumena sjene na grafičkoj kartici. Zbog masivno paralelne arhitekture grafičkih procesora, ovime se postiže znatno ubrzanje algoritma. Međutim, i dalje ostaje problem iscrtavanja, odnosno rasterizacije volumena sjene pri generiranju spremnika šablone. Naime, budući da se volumeni sjene stvaraju na temelju geometrije scene, i to za svako svjetlo posebno, geometrijska kompleksnost scene ima direktan i značajan utjecaj na performanse. Već i sa samo tri ili četiri izvora svjetla na sceni, govorimo o trostrukom ili četverostrukom povećanju broja vrhova koje je potrebno obraditi. Međutim, poseban je problem što pojedini volumen sjene zauzima mnogostruko veći prostor od objekta koji ga opisuje. Teoretski, volumen sjene je beskonačan, na u praktičnim primjenama odrezuje se na neku dovoljnu dubinu, tako da je pokrivena kompletna scena. Zbog svoje veličine, volumeni sjene zahtijevaju znatan utrošak vremena na rasterizaciju.

S druge strane, algoritam preslikavanja sjena ima bitno drugačija svojstva, budući da se zasniva na drugačijem principu. Naime, ideja je sljedeća: scenu možemo iscrtati kao da je promatramo iz pozicije svjetla, i pritom za svaki fragment odrediti samo dubinu, bez računanja boje, odnosno osvjetljenja. Tako nastali spremnik dubine naziva se mapa sjene (otuda i naziv algoritma). Dakle, u mapi sjene zapravo imamo prikaz reljefa scene, u prostoru svjetla. U sljedećem koraku, scena se iscrtava na standardni način, ali prilikom izračunavanja osvjetljenja potrebna je dodatna provjera zaklonjenosti danog fragmenta, pomoću mape sjene. Tek ukoliko fragment nije zaklonjen, računa se osvjetljenje - u suprotnom slučaju, fragment se ne osvjetljava. Dakako, preostalo je pitanje kako iskoristiti mapu sjene, odnosno, izvršiti provjeru leži li dani fragment u sjeni ili ne. Postoji nekoliko različitih varijanti algoritma koje drugačije rješavaju ovo pitanje. U svom osnovnom, najjednostavnijem obliku, postupak se sastoji od tri koraka:

1.      Rekonstrukcija pozicije fragmenta u prostoru kamere

2.      Transformacija pozicije fragmenta iz prostora kamere u prostor svjetla

3.      Usporedba z komponente pozicije fragmenta s vrijednosti u mapi sjene

Prvi korak je trivijalan u slučaju korištenja unaprijednog iscrtavanja, budući da se vrhovi i fragmenti obrađuju u istom prolazu, pa je moguće jednostavno prenijeti podatak o poziciji vrha iz programa za sjenčanje vrhova u program za sjenčanje fragmenata. U slučaju iscrtavanja s odgodom, potrebno je rekonstruirati poziciju u prostoru kamere iz položaja fragmenta u prostoru slike, te spremnika dubine. Kao kratki podsjetnik, transformacija vrhova geometrije se provodi na sljedeći način:

Početno, zadane su koordinate vrhova u lokalnom koordinatnom sustavu objekta kojem ti vrhovi pripadaju. Postavljanjem objekta na scenu, definira se transformacija iz prostora objekta u prostor scene. Konačno, postavljanjem kamere na scenu, definira se transformacija iz prostora scene u prostor kamere, čime je faza transformacije završena. Zatim, slijedi projekcija iz prostora kamere u neki projekcijski volumen, primjerice kvadar za ortogonalnu projekciju, ili (krnju) piramidu za perspektivnu projekciju. Budući da se koriste homogene koordinate (x, y, z, w), potrebno je izvršiti normalizaciju, dijeljenjem s w koordinatom, čime se prelazi u normalizirani prostor projekcije, gdje su sve koordinate u intervalu [0, 1]. Napokon, skaliranjem i translacijom pomoću parametara zaslona, prelazi se u prostor slike. Primjerice, za rezoluciju zaslona 800x600, x koordinata u prostoru slike je u intervalu [0, 800], a y koordinata u intervalu [0, 600]. Dakle, za rekonstrukciju pozicije fragmenta u prostoru kamere, potrebno je izvršiti inverznu projekciju, što je najjednostavnije učiniti množenjem koordinata fragmenta u prostoru slike, i dubine, s inverznom matricom projekcije. Nakon transformacije rekonstruirane pozicije fragmenta u prostor svjetla, moguće je provesti sam test zaklonjenosti. Ukoliko je dubina danog fragmenta u prostoru svjetla veća nego vrijednost u mapi sjene, zaključujemo da je fragment zaklonjen, budući da je na danoj poziciji izvoru svjetla bio bliži neki drugi objekt (čija je dubina zapisana u mapi sjene).

Dakle, za razliku od volumena sjena, kod preslikavanja sjena nije potrebno generirati i iscrtavati dodatnu geometriju za svaki izvor svjetla, već je dovoljno iscrtati samo početnu geometriju scene, i pritom generirati samo spremnik dubine, kao zasebnu teksturu za svako svjetlo. Iz tog razloga, preslikavanje sjena općenito pruža bolje performanse od volumena sjena, te se češće koristi u komercijalnim igrama i aplikacijama. Međutim, u svom osnovnom obliku, algoritam pokazuje određene neprihvatljive nedostatke. Naime, budući da je mapa sjena točno određene, konačne rezolucije (primjerice, 512x512 slikovnih elemenata), na sjenama se često pojavljuju nazubljeni rubovi. Problem je dodatno naglašen činjenicom da sjene nije moguće prikazati jednolikom rezolucijom u mapi sjena - nakon transformacije pozicije fragmenta u prostor svjetla, moguće je da veći broj fragmenata (šira regija u prostoru slike) upada na istu (užu) regiju u mapi sjene, što dakako, ovisi o poziciji i upadnom kutu svjetla. Ovo je poseban pod-problem, za kojeg je razvijeno nekoliko rješenja. Primjerice, kod trapezoidalnih mapa sjena (eng. trapezoidal shadow maps), algoritam pronalazi optimalnu projekciju scene na mapu sjena, iz pogleda izvora svjetla, i time osigurava bolju iskoristivost razlučivosti mape sjena. Drugačiji pristup, koji je posebice pogodan za vrlo velike, otvorene scene, su kaskadirane mape sjena (eng. cascaded shadow maps), a koji se sastoji od particioniranja scene na više regija, i to tako da je svaka regija prikazana zasebnom mapom sjena. Sve mape sjena unutar kaskade su jednake rezolucije, ali regije zauzimaju progresivno veći prostor što su dalje od promatrača, tako da je u neposrednoj blizini promatrača broj slikovnih elemenata mape sjene po jedinici prostora najveći, te s udaljenosti taj broj opada. Dakle, ideja je slična tehnici razine detalja (eng. level of detail, LoD) kod iscrtavanja udaljene geometrije.

Međutim, čak i uz dovoljnu veličinu i razlučivost mape sjena, rubovi sjena će i dalje biti oštri, što izgleda neprirodno. Prema tome, potrebno je zamutiti rubove sjena i tako dobiti mekše, prirodnije sjene - drugim riječima, potrebno je izvršiti filtriranje mape sjena. Upravo u ovom dijelu razlikuju se različite varijante osnovnog algoritma. Tradicionalan pristup, koji je bio sklopovski implementiran na grafičkim karticama (na sličan način kao sklopovsko izglađivanje nazubljenih rubova poligona), bazira se na uzorkovanju i testiranju nekoliko susjednih uzoraka u mapi sjena (eng. percentage closer filtering, PCF). Dakle, PCF algoritam proširuje osnovno preslikavanje sjena tako da provjeru zaklonjenosti fragmenta izvrši nekoliko puta, i to s različitim, susjednim elementima mape sjena. Uzorci se obično uzimaju u pravilnoj rešetki, primjerice 4x4, odnosno, ukupno 16 uzoraka po fragmentu. Rezultati svih usporedbi se pomnože odgovarajućim težinskim faktorom te zbroje, i time se dobije konačan rezultat koji više nije binarna vrijednost (zaklonjen / nije zaklonjen), već decimalan broj u intervalu [0, 1], gdje nula predstavlja potpunu sjenu, a jedinica potpunu osvijetljenost. Dakle, ono što zapravo dobijemo kao rezultat PCF algoritma jest postotak uzoraka unutar regije uzorkovanja čije je dubina veća od one u mapi sjena. Prema tome, jasno je da rubovi sjena više neće biti oštri (niti nazubljeni!), već blago zamućeni. Dakako, cijena ovog algoritma je potreba za dodatnim, višestrukim uzorkovanjem, koje je potrebno provoditi pri svakoj provjeri.

No, postoji još jedna, relativno nova varijanta algoritma preslikavanja sjena, koja pruža bolje performanse uz jednaku ili čak bolju kvalitetu. Riječ je o preslikavanju sjena temeljenom na izračunu varijance dubine scene zapisane u mapi sjena (eng. variance shadow maps, VSM). Naime, umjesto jednostavne usporedbe dubine fragmenta s vrijednosti u mapi sjena, vrši se analiza distribucije vrijednosti dubina u mapi sjena. Ideja se zasniva na opažanju da kod PCF algoritma, ono što želimo dobiti kao rezultat jest udio zaklonjenih uzoraka u skupu svih uzoraka neke regije. Drugim riječima, uspoređujemo vrijednost dubine danog fragmenta, sa skupom vrijednosti dubina uzoraka. Ovako postavljen problem veoma podsjeća na definiciju funkcije distribucije vjerojatnosti, koja se matematički formulira na sljedeći način:

Ukoliko bi distribucija vrijednosti dubina u mapi sjena bila poznata, onda usporedbe pojedinih uzoraka ne bi bile potrebne - dovoljno bi bilo tek evaluirati funkciju distribucije vjerojatnosti nad danim fragmentom. Jasno, problem je što je distribucija nepoznata, pa je to nemoguće - mogli bismo pretpostaviti neku funkciju distribucije, no to vrlo vjerojatno ne bi proizvelo zadovoljavajuće rezultate za proizvoljne scene. Međutim, sada se valja prisjetiti Čebiševljeve nejednakosti, koja kaže da za bilo koju distribuciju vjerojatnosti, većina vrijednosti će biti blizu očekivane vrijednosti. Točnije, ne više od  vrijednosti će biti udaljeno više od k standardnih devijacija od očekivane vrijednosti. Dakle, ovim teoremom možemo odrediti gornju granicu vrijednosti funkcije distribucije vjerojatnosti  za danu vrijednost x. Drugim riječima, možemo odrediti gornju granicu udjela zaklonjenih uzoraka u nekom skupu. Korisnost Čebiševljeve nejednakosti leži u činjenici da je primjenjiva na proizvoljnu, nepoznatu distribuciju, za koju je poznato barem očekivanje i varijanca. U našem slučaju, očekivanje se može jednostavno definirati kao aritmetička sredina svih uzoraka. Varijanca se može trivijalno izvesti iz očekivanja:

Konačno, Čebiševljevu nejednakost možemo formulirati na sljedeći način:

U našem slučaju, t će biti dubina promatranog fragmenta, E(x) aritmetička sredina vrijednosti dubina neke regije uzorkovanja, a σ² varijanca te regije. Prema tome, skupo višestruko uzorkovanje PCF algoritma se zamjenjuje evaluacijom izraza (3). Dakako, jedino preostalo pitanje je kako točno izračunati i pohraniti očekivanje i varijancu. Ovaj korak je jednostavan - dovoljno je proširiti teksturu mape sjena tako da sadrži dva kanala, umjesto samo jednog. Prvi kanal, kao i dosad, sadrži dubinu scene dobivenu iscrtavanjem iz pogleda svjetla. U drugi kanal, zapisuje se kvadrat te dubine. Zatim, potreban je podprolaz zamućivanja mape sjena, jednostavnim zbrajanjem uzoraka i podjelom s njihovim brojem, koristeći primjerice rešetku uzorkovanja dimenzija 15x15 elemenata. Jasno, ovim zamućivanjem zapravo dobivamo očekivanje, te budući da u teksturi pohranjujemo i dubinu, i kvadrat dubine, odmah dobivamo E(x) u prvom kanalu, te E(x²) u drugom kanalu teksture. Zatim, prilikom izračuna osvjetljenja, E(x) i E(x²) se jednostavno očitaju iz mape sjena te se trivijalno odredi varijanca prema izrazu (2), nakon čega je moguće evaluirati formulu (3), ukoliko je zadovoljen uvjet da je dubina fragmenta veća od očekivanja. U suprotnom, jednostavno se uzima P(x ≥ t) = 1.

Usporedbom PCF i VSM algoritma, možemo zaključiti da oba teže k istom rezultatu, no drugačijim postavljanjem problema kod VSM algoritma, omogućeno je obavljanje filtriranja mape sjena u zasebnom pred-koraku. Prava prednost ovog pristupa jest činjenica da je sada moguće primijeniti separabilnu jezgru zamućivanja. Naime, kod PCF algoritma, budući da se filtriranje obavlja u istom prolazu kao i izračun osvjetljenja, dakle u jednom prolazu, kompleksnost je kvadratna - za 4x4 rešetku, potrebno je obaviti 16 uzorkovanja. Međutim, ukoliko filtriranje obavljamo kao zaseban prolaz, moguće ga je razbiti u dva podprolaza, tako da u prvom podprolazu zamućujemo originalnu teksturu samo u vertikalnom smjeru, a u drugom podprolazu zamućujemo vertikalno zamućenu teksturu u horizontalnom smjeru. Na taj način, kompleksnost filtriranja postaje linearna, budući da je ukupan broj koraka jednak zbroju vertikalne i horizontalne dimenzije rešetke uzorkovanja. Primjerice, za 15x15 rešetku, separabilnim filtriranjem kod VSM algoritma dovoljno je 30 uzorkovanja po fragmentu, dok bi jednoprolaznim filtriranjem kod PCF algoritma bilo potrebno čak 225 uzorkovanja, što nije praktički izvedivo ni na modernim grafičkim karticama. Prema tome, VSM algoritmom možemo uz jednake performanse postići mnogo kvalitetnije filtriranje sjena - ili, uz jednaku kvalitetu, mnogo bolje performanse nego kod PCF algoritma.

Međutim, u ovom trenutku treba spomenuti i određene artefakte koji se javljaju primjerice kod dvostrukih sjena, tj. dijela prostora koji je zaklonjen dvjema različitim objektima.

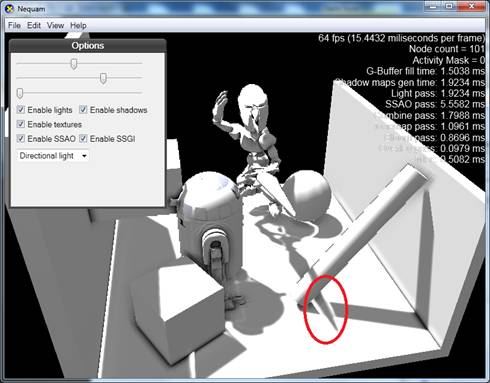
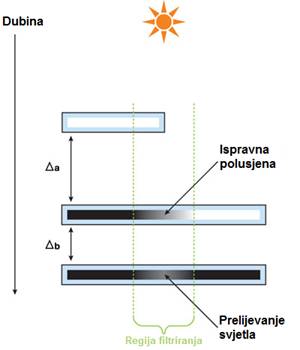
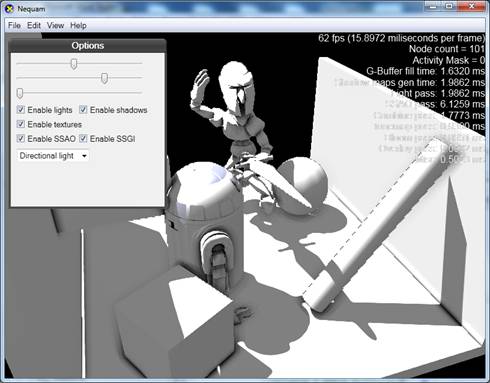
Kao što se vidi na Slici 15, u takvim situacijama dolazi do prelijevanja svjetla (eng. light bleeding), budući da se meki rub sjene preslikava dijelom na prvi zaklonjeni objekt (sjena mača na položenoj cijevi), a dijelom na drugi zaklonjeni objekt (sjena mača na podu, na mjestu gdje sječe sjenu cijevi). Razlog zašto se ovo događa, jest taj što unutar iste regije filtriranja upadaju elementi mape sjena generirani i prvim i drugim objektom, pa zbog zamućivanja oba postaju sivi (polusjena). Ova se pojava najlakše objašnjava sljedećom slikom:

Srećom, postoji jednostavno rješenje ovog problema koje je gotovo trivijalno (i u smislu implementacije, i u smislu računalne zahtjevnosti), a pruža dovoljno dobre rezultate za većinu stvarnih primjena. Naime, ukoliko ponovno razmotrimo Čebiševljevu nejednakost, možemo uočiti da ukoliko je dani fragment u potpunosti zaklonjen, vrijedit će t > E(x). Prema tome, vrijedi (t - E(x))² > 0, a što znači da je konačno P(x ≥ t) < 1. Drugim riječima, polusjene (točne ili netočne) nikada neće doseći punu zaklonjenost P(x ≥ t) = 1 dok je zadovoljen uvjet t > E(x), dakle na potpuno zaklonjenim fragmentima. Iz navedenog slijedi jednostavna ideja - možemo se riješiti netočnih osvijetljenih područja gdje je P(x ≥ t) blizak nuli, tako da definiramo prag P_min, kao korisničku varijablu. Nakon evaluacije izraza (3), odrezat ćemo dobivenu vrijednost ukoliko upada u interval [0, Pmin], te skalirati s intervala (Pmin, 1] natrag na [0, 1]. Rezultat jest taj, da će sve polusjene općenito postati tamnije, što znači da će doći do gubitka detalja. No, pažljivim namještanjem parametra Pmin za danu scenu, moguće je postići da artefakti gotovo u potpunosti nestanu, uz tek neznatan gubitak detalja kod polusjena. Primjer identične scene kao u slici 15, ali uz navedenu korekciju polusjena dan je slikom 17.

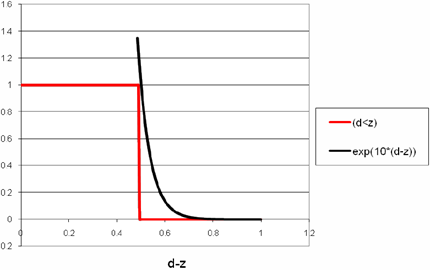
Na kraju, valja istaknuti kako je koncept preslikavanja sjena predstavljen još 1978 godine (Lance Williams), no ovo područje računalne grafike se još uvijek aktivno istražuje. Primjerice, jedan od novijih pokušaja [Annen07] su konvolucijske mape sjena (eng. convolution shadow maps, CSM), koje se bazira na opažanju da je funkcija testa zaklonjenosti zapravo step funkcija , gdje je z dubina fragmenta, a d dubina u mapi sjena. Ideja algoritma jest, da je ovu funkciju moguće aproksimirati konačnim Furierovim redom. Dakle, CSM algoritam zahtjeva n-komponentnu mapu sjena (gdje je n broj članova Furierovog reda), tako da je u svakoj komponenti kodiran pojedini član reda. Na taj način, opet je omogućeno separabilno predfiltriranje mape sjena. Premda CSM algoritam ne pokazuje problem prelijevanja svjetla, dolazi do drugih artefakata zbog aproksimacije nepotpunim Furierovim redom, koje je mnogo teže maskirati. Dakako, takve artefakte je moguće umanjiti uzimanjem većeg broja članova, no to povlači i povećanu potrošnju memorije (svaki dodatni član zahtjeva dodatni teksturni kanal), te zahtjevniji korak predfiltriranja (budući da je potrebno obraditi veći broj teksturnih kanala). Slična, novija ideja [Salvi08] jest aproksimacija funkcije zaklonjenosti (step funkcije) pomoću jednostavne eksponencijalne funkcije (eng. exponential shadow maps, ESM). Naime, sljedeći graf zorno prikazuje ovu ideju:

Kao što gornja slika prikazuje, funkcija oblika  može biti dovoljno "slična" step funkciji za odgovarajuću konstantu α. Dakle, slično kao kod CSM algoritma, ESM zahtjeva pohranu dubine scene prikazane aproksimacijskom funkcijom u mapi sjena. No, ovdje je razlika što je dovoljan tek jedan teksturni kanal, što znači smanjeni utrošak memorije, te brže filtriranje. I kod ESM algoritma se mogu javiti artefakti, primjerice pojava svijetlih regija - na slici 17, step funkcija opada trenutačno u nulu nakon prelaska određenog praga, no eksponencijalna funkcija postepeno opada, te je u određenom intervalu iza praga još uvijek iznad nule. Ovaj se problem može riješiti pažljivim namještanjem parametra α za danu scenu, dakle slično kao kod VSM algoritma.

Zbog svojih odličnih svojstava, preslikavanje sjena se nametnulo kao standardna metoda za rješavanje direktnih sjena. Danas možda najpopularnija inačica algoritma jest VSM, budući da je to prva metoda koja je omogućila separabilno pred-filtriranje, što je rezultiralo znatnim poboljšanjem i kvalitete i performansi, te je algoritam vrlo dobro dokumentiran i prihvaćen od strane razvijatelja. No, ovo se područje i dalje intenzivno razvija, te već postoje nova, obećavajuća poboljšanja kao što je ESM algoritam.