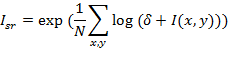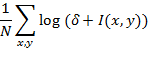Diplomski rad br. 5

U prethodnim poglavljima, promatrani su modeli lokalnog osvjetljenja, te postupci izračunavanja tih modela. Međutim, ono što nije bilo posebno promotreno jest problem ograničene preciznosti grafičkog sklopovlja i računalnih zaslona. Naime, u stvarnom svijetu, omjer najvećeg i najmanjeg intenziteta osvjetljenja koje se javlja u svakodnevnom životu je vrlo visok, i iznosi otprilike 10¹² : 1. Ovaj omjer se naziva dinamički raspon, te u kontekstu računalne grafike, definira potrebnu preciznost za točan prikaz svih razina osvjetljenja. Za dani primjer, ukupno bi bilo potrebno barem  bitova za očuvanje dinamičkog raspona. Međutim, postojeći moderni računalni zasloni su u prosjeku sposobni za prikaz dinamičkog raspona od svega 10² : 1, za čiji prikaz je dovoljno  bitova. Budući da 8-bitni cijeli brojevi pružaju dostatnu preciznost za ovaj raspon, a operacije nad njima su vrlo brze, upravo je takav tip podataka definiran kao standardni format za zapis boje slikovnih elemenata (dakle, 8 bitova po R, G, B, A kanalima, ukupno 32 bita po slikovnom elementu). Rane grafičke kartice su podržavale pohranu i operacije nad fragmentima isključivo u navedenom formatu, što je dostatno za zapis slike prikazane na zaslonu. Međutim, jasno je da pri računanju osvjetljenja u ograničenoj preciznosti dolazi do značajnog gubitka informacija - odličan primjer scene kod koje se javlja ovaj problem jest zatvoreni, tamni prostor u kojeg upada jarka, vanjska svjetlost kroz neki otvor, tako da je dinamički raspon scene vrlo visok. Dakako, čak i kada bismo računali osvjetljenje u dovoljnoj preciznosti za očuvanje cjelokupnog dinamičkog raspona, te rezultate ne bismo mogli direktno prikazati na zaslonu. Područja koja bi bila presvijetla bi bila odrezana na maksimalnu vrijednost, a ostatak zaokružen na najbližu od 256 diskretnih razina osvjetljenja po kanalu, gubeći pritom mnoge detalje. Upravo ovaj problem rješava postupak tonskog preslikavanja. No, prije objašnjenja tog postupka, bilo bi korisno upoznati se s određenim osnovnim svojstvima ljudskog vida. Naime, niti ljudsko oko nije sposobno jednoliko zapažati detalje u cjelokupnom dinamičkom rasponu kakav se javlja u stvarnom svijetu. Štoviše, sposobnost opažanja ljudskog oka je ograničena na uzak raspon od otprilike 10³ : 1. Ipak, čovjek je sposoban opažati detalje i u relativno mračnom, i u jarko osvijetljenom prostoru - ali ne istovremeno u oba. Ključ ove sposobnosti leži u mogućnosti adaptacije oka, tako da opažajni raspon oka pokriva onaj dio dinamičkog raspona osvjetljenja, koji ima najveći utjecaj na scenu, odnosno, u kojem se nalazi najviše detalja. Dakle, ljudsko oko se zapravo prilagođava srednjoj vrijednosti intenziteta upadne svjetlosti. Ovaj princip se koristi i u fotografiji, gdje se definira pojam ekspozicije, kao ukupne dozvoljene količine svjetlosti koja upada na fotografski medij. Idealno, cilj je da ekspozicija fotografije odgovara srednjoj vrijednosti intenziteta osvjetljenja fotografirane scene. U protivnom, moguća su dva pogrešna slučaja. U prvom slučaju, ekspozicija je previsoka, slika je presvijetla, te su u najsvjetlijim područjima detalji izgubljeni (potpuno bijela područja); u drugom slučaju, ekspozicija je preniska, slika je pretamna, te su u najtamnijim područjima detalji izgubljeni (potpuno crna područja). Ove pojave se najlakše uočavaju naglim prijelazom iz vrlo svijetlog u vrlo tamni prostor (ili obrnuto) - budući da adaptacija ljudskog oka traje određeno vrijeme, slika koju ćemo isprva vidjeti će biti preniske ili previsoke ekspozicije.

Upravo opisani princip se koristi u postupku tonskog preslikavanja. Naime, osvjetljenje izračunato u visokoj preciznosti, potrebno je preslikati u nizak dinamički raspon kakav se može prikazati na zaslonu. Dakle, problem je ekvivalentan adaptaciji ljudskog oka, stoga možemo koristiti isto rješenje - u prvom koraku, izračunat ćemo srednji intenzitet osvjetljenja scene, i na temelju toga potrebnu ekspoziciju. U drugom koraku, primijenit ćemo određeni ne-linearni operator nad fragmentima visokog raspona, te dobiti fragmente niskog raspona, takve da tvore sliku tražene ekspozicije. Konačni rezultat jest očuvanje detalja koji bi inače bili izgubljeni, da su svi izračuni osvjetljenja bili izvršeni u niskoj preciznosti. Primjer scene za koju iscrtavanje HDR osvjetljenjem (eng. high dynamic range) znatno poboljšava kvalitetu u odnosu na iscrtavanje LDR osvjetljenjem (eng. low dynamic range) jest dan slikom 10.

Premda je algoritam tonskog preslikavanja konceptualno vrlo jednostavan, pravilna implementacija nije tako jednostavna za izvesti. Dakako, prvi korak je odabir odgovarajućeg formata za pohranu fragmenata. Moderne grafičke kartice nude 16- i 32-bitnu preciznost po kanalu boje, dakle ukupno 64 ili 128 bita po fragmentu, uz korištenje standardizirane aritmetike pomičnog zareza. Veća preciznost povlači lošije performanse i dvostruko veću potrošnju memorije, ali niža preciznost može uzrokovati pojavu artefakata. Jednom kad je odabran zadovoljavajući format, svi G-spremnici moraju biti kreirani istim formatom, osim konačnog spremnika okvira, koji mora imati 8-bitnu preciznost po kanalu boje (radi prikaza na zaslonu). Zatim, potrebno je definirati dodatan prolaz koji će se izvoditi nakon što je generirana konačna osvijetljena slika (dakle, nakon svih prolaza osvjetljenja) - budući da će ta slika biti visokog dinamičkog raspona (HDR), potrebno je implementirati program za sjenčanje fragmenata koji će izvršiti tonsko preslikavanje, i generirati ekvivalentnu sliku niskog dinamičkog raspona (LDR). Kako je rečeno, prvi korak ovog postupka se sastoji od izračuna srednje vrijednosti intenziteta osvjetljenja, za što možemo koristiti sljedeću formulu:

gdje je I_sr srednji intenzitet osvjetljenja, N ukupan broj fragmenata, δ neka malena vrijednost, a I(x, y) boja fragmenta na poziciji (x, y). Broj δ je potreban za slučaj potpuno crnih fragmenata, odnosno I(x, y) = 0. Međutim, postavlja se pitanje - kako evaluirati gornju formulu nad spremnikom u obliku teksture u memoriji grafičke kartice? Srećom, postoji jednostavan trik kojeg možemo koristiti. Naime, dovoljno je predprolazom izračunati logaritam svakog fragmenta HDR slike i te vrijednosti zapisati u novu teksturu, što je trivijalno izvedivo vrlo jednostavnim programom za sjenčanje fragmenata. Zatim, upotrebom ugrađene funkcionalnosti grafičke kartice, potrebno je generirati kompletan mip lanac dobivene logaritamske teksture, za što je dovoljan tek jedan funkcijski poziv. Naime, mip preslikavanjem se početna tekstura sažimlje u teksturu dvostruko manjih dimenzija, na način da je svaki fragment umanjene teksture dobiven kao srednja vrijednost četiriju odgovarajućih susjednih fragmenata početne teksture. Ovaj se postupak može ponavljati sve dok se ne dobije tekstura dimenzija 1x1, čime se dobije niz uzastopno umanjenih tekstura koji se naziva mip lanac. Dakle, u konačnoj teksturi mip lanca, zapravo je sadržana srednja vrijednost ukupne početne slike. Prema tome, generiranjem mip lanca logaritamske teksture dobivamo u završnoj teksturi konačnu vrijednost izraza:

Za izračun konačne vrijednosti I_sr, te provedbu samog tonskog preslikavanja originalne HDR slike scene, potreban je još jedan prolaz, sa zasebnim programom za sjenčanje fragmenata. U ovom prolazu, prvi korak je dakako učitavanje vrijednosti završne teksture prethodno generiranog mip lanca, te izračun srednje vrijednosti intenziteta osvjetljenja, jednostavnim antilogaritmiranjem. Nakon toga, potrebno je izvršiti linearno skaliranje HDR fragmenta na temelju zadane, tražene ekspozicije, pomoću izraza:

gdje je α tražena ekspozicija, a I_s(x, y) skalirana boja fragmenta (x, y). Valja uočiti da smo ovime linearno preslikali boju fragmenta u interval centriran oko tražene ekspozicije, no taj interval nije nužno [0, 1], kakav mora biti za prikaz na zaslonu, već općenito [0, ∞). Prema tome, potrebno je još odabrati odgovarajući nelinearni operator koji će izvršiti preslikavanje [0, ∞) → [0, 1]. Najjednostavniji takav operator koji se često koristi dan je sljedećim izrazom:

Sada je još jedino preostalo pitanje kako odabrati odgovarajuću ekspoziciju. Jasno, moguće je jednostavno uzeti da ekspozicija odgovara izračunatoj srednjoj vrijednosti intenziteta osvjetljenja scene, što je zapravo idealni slučaj u fotografiji. No, moguće je i simulirati adaptaciju ljudskog oka na nagle promjene u osvijetljenosti, na način da promjena ekspozicije kasni za promjenom srednjeg intenziteta osvjetljenja, što se može postići postepenom promjenom ekspozicije kroz nekoliko slikovnih okvira (eng. frame).

Dodatan efekt koji se javlja u stvarnim lećama, a kojeg je jednostavno implementirati uz HDR osvjetljenje, jest pojava prelijevanja svjetla. Naime, čak i kod idealnih leća, javlja se artefakt nazvan Airyev uzorak, koji nastaje zbog difrakcije svjetla koje upada na okruglu leću, a rezultira pojavom središnjeg svijetlog kruga i alternirajućih tamnih i svijetlih pojaseva, oko jarko osvijetljenih objekata. Primjer ovog artefakta dan je slikom 11:

Međutim, realne leće nikada nisu savršeno fokusirane, tako da je i ovaj artefakt zamućen, te prijelazi između pojedinih svijetlih pojaseva nisu primjetni, kako prikazuje sljedeća, stvarna fotografija (slika 12):

Iz gornjih opažanja, proizlazi ideja praktične implementacije pojave prelijevanja svjetla. Dakle, budući da već računamo osvjetljenje fragmenata u visokom dinamičkom rasponu, moguće je dodati još jedan prolaz kojim ćemo odbaciti tamne fragmente, a zadržati samo vrlo svijetle; drugim riječima, primijenit ćemo visoko-propusni filtar nad HDR slikom. Rezultirajuću sliku je zatim potrebno nekoliko puta uzastopno zamutiti, primjenom Gaussovog zamućivanja. Konačni rezultat je aproksimacija zamućenog Airyevog uzorka kakav se javlja u stvarnim lećama kod jarko osvijetljenih objekata. Na kraju, dobivenu zamućenu sliku je potrebno jednostavno zbrojiti s LDR slikom (dobivenom tonskim preslikavanjem), i rezultat je slika s efektom prelijevanja svjetla. Za uštedu vremena obrade i memorije, dovoljno je gornje korake izvršiti nad HDR slikom smanjenih dimenzija (dvostrukim ili trostrukim mip preslikavanjem), budući da ionako vršimo zamućivanje.

Na kraju, potrebno je još razmotriti problem izglađivanja nazubljenih rubova poligona. Naime, HDR osvjetljenje je moguće implementirati i s unaprijednim iscrtavanjem, i s iscrtavanjem s odgodom. Međutim, čak i kod unaprijednog iscrtavanja, nije moguće koristiti ugrađene, sklopovske mehanizme izglađivanja višestrukim uzorkovanjem, budući da su opet potrebna dva prolaza za računanje konačnih, osvijetljenih fragmenata. Dakle, u prvom prolazu bila bi obrađena geometrija scene i  izračunati HDR fragmenti, a u drugom prolazu izvedeno tonsko preslikavanje (što je obrada slike), i tako dobiveni LDR fragmenti. Budući da se sklopovsko izglađivanje automatski provodi u prolazu u kojem se obrađuje geometrija, dobili bismo "izglađene" HDR fragmente. Problem je u tome što nad tim fragmentima moramo provesti tonsko preslikavanje, što nije linearna operacija - dakle, rezultati neće biti isti kao kada bismo izglađivanje proveli nakon tonskog mapiranja. Drugim riječima, dobili bismo pogrešne rezultate, što znači da opet moramo koristiti mogućnost ručnog pristupa pojedinim višestrukim uzorcima koju nudi DirectX 10 (vidjeti poglavlje 4).