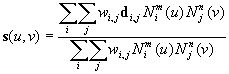2. NURBS površine
Površinu je najlakše predstaviti krivuljom koja putuje kroz prostor i pritom mijenja oblik. Sama krivulja može biti predstavljena kao jednostavna Bézier-ova krivulja ili kao b-spline krivulja. B-spline krivulja je krivulja koja se sastoji od niza polinomijalnih segmenata. Promjena oblika krivulje postiže se tako da se svaki pojedinačni kontrolni vrh (kontrolni vrhovi definiraju oblik krivulje) giba po također Bézier-ovoj ili b-spline krivulji. Slijedeća jednadžba prikazuje matematički zapis bikubne b-spline površine:
Ova površina predstavljena je pomoću kubne b-spline krivulje čiji kontrolni vrhovi se gibaju po također kubnoj b-spline krivulji. Sa di,j su označene kontrolne točke. Sa Ni(u) i Nj(v) su označene vezne funkcije u u i v smjeru.
Sa 
je definirana kubna
b-spline krivulja koja definira krivulju koja se giba dok su sa 
definirane kubne b-spline krivulje po
kojima se kontrolni vrhovi prve krivulje gibaju.Vezne funkcije imaju ulogu
težinskih funkcija koje prikazuju koliko jako kontrolni vrhovi privlače krivulju u
svojoj blizini. Mijenjanjem širine i visine pojedinih veznih funkcija postiže se da
pojedini kontrolni vrhovi jače ili slabije privlače krivulju u svojoi okolini
čime se postiže veća kontrola nad samom krivuljom. Ako su vezne funkcije različitih
širina i visina tada se radi o neuniformnim b-spline krivuljama odnosno površinama.
Dodatnu kontrolu nad krivuljom odnosno nad površinom moguće je postići uvođenjem četvrte koordinate. 3D površina prikazuje se kao projekcija četverodimenzionalne površine u 3D prostor. Na ovaj način moguće je dobiti površine dobivene rotacijom krivulje oko proizvoljne osi. Ovako definirane površine nazivaju se racionalne površine.
Neuniformne racionalne b-spline površine najčešće se nazivaju NURBS površine. Matematički ovakve površine se zapisuju pomoću slijedeće jednadžbe:
