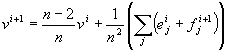
3. Površine nastale podjelom poligona
Kada se govori o postupcima podjele poligona tada se osim podjele početnih poligona na niz manjih podrazumijeva i uglađivanje oštrih bridova pomicanjem odgovarajućih vrhova. Danas je poznat veliki broj shema podjele poligona (Doo-Sabin, Catmull-Clark, Loop, Butterfly, modificirana Butterfly shema, Midedge, Kobbelt i dr.), a ovdje će ukratko biti opisane tri najpoznatije sheme: Catmull-Clark, Loop i modificirana Butterfly shema.
Catmull-Clark shema podjele poligona
Nastala je 1978. godine kao poboljšanje Doo-Sabinove sheme koja je nastala iste godine. Autori E. Catmull i J. Clark koriste generalizaciju uniformne bikubne b-spline krivulje kako bi definirali pravila podjele poligona. Dobivena shema podjele poligona je aproksimativna četverokutna shema što znači da kontrolni vrhovi nikad ne leže na površini dobivenoj podjelom poligona i da ova shema producira uvijek četverokutne poligone.
Sama podjela može se opisati u tri koraka:
korak - računanje rubnih točaka kao srednje vrijednosti četiriju točaka: dviju središnjih točaka s obje strane brida i dviju rubnih točaka koje omeđuju brid korak - računanje novog položaja kontrolnog vrha na temelju slijdeće jednadžbe:
- korak - računanje središnje točke poligona kao srednje vrijednosti vrhova koji tvore taj poligon
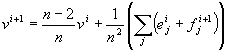
Oznaka i označava korak podjele, sa v je označen kontrolni vrh kojem se mijenja položaj, sa e su označeni kontrolni vrhovi koji se spajaju s vrhom v, dok su sa f označene središnje točke poligona kojima je vrh v sastavni dio. Sa n je označena spojnost vrha v. Spojnost označava broj bridova koji izalaze iz nekog vrha.
Dobivena površine ima C2 kontinuitet u regularnim vrhovima (vrhovi spojnosti četiri) dok u izvanrednim vrhovima (vrhovi čija je spojnost različita od četiri) ima C1 kontinuitet. Općenito se za površinu kaže da ima Cn kontinuitet ako u svakoj točki površine ima definiranu n-tu derivaciju.
Loop shema podjele poligonaLoop shema nastala je 1987. godine kao generalizacija trokutnog b-spline-a četvrtog stupnja. Ime je dobila prema autoru Charles-u Loop-u. Loop shema je aproksimativna trokutna shema, dakle producira uvijek trokutne poligone. Ova shema ujedno je i ograničena samo na trokutne poligonalne mreže, no to ne predstavlja ograničenje budući da se svaki n-terokutni poligon, gdje je n>3, može rastaviti na odgovarajući broj trokutnih poligona.
Podjela se može opisati u dva koraka:
korak - računanje novog položaja kontrolnih vrhova kao srednje vrijednosti položaja samog vrha i vrhova koji ga neposredno okružuju pomnoženih odgovarajućim težinskim faktorima. Težinski faktori ovise o spojnosti vrha čiji se položaj mijenja pa su stoga dane dvije izračunske maske s pripadajućim težinskim vrijednostima: jedna za slučaj regularnog vrha (u trokutnim shemama vrh spojnosti šest) i jedna za slučaj izvanrednog vrha. Izračunska maska predstavlja šablonu koja prekriva vrhove koji će ući u proračun.
Slika 1. Izračunske maske Loop sheme u slučaju regularnog i izvanrednog vrha
Vrh kojem se mijenja položaj naznačen je punim kružićem. Sa n je označena spojnost vrha a.
Slika 2. Izračunska maska Loop shema za izračun rubne točke
Površina ima C2 kontinuitet u regularnim vrhovima, dok u izvanrednim vrhovima ima samo C1 kontinuitet.
Modificirana Butterfly shema podjele poligona
Godine 1990. predstavljena je Butterfly shema. Autori su Dyn, Levin i Gregory. Nastala je generalizacijom trokutnog b-spline-a trećeg stupnja. Shema je interpolacijska i trokutna što znači da se kontrolni vrhovi uvijek nalaze na površini nastaloj podjelom poligona te slično kao i Loop shema producira trokutne poligone. Ova shema je ujedno jedina predstavnica interpolacijskih shema. Ime je dobila prema obliku izračunske maske koja podsjeća na leptira. Na slijedećoj slici prikazana je izračunska maska Butterfly sheme s odgovarajućim težinskim faktorima:
![]()
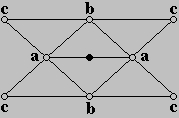
Slika 3. Izračunska maska Butterfly sheme
Punim kružićem naznačena je nova točka koja se računa na temelju vrhova koje obuhvaća izračunska maska. Sa w je označen parametar napetosti (eng. tension parametar) koji definira kako je čvrsto površina nastala podjelom nategnuta prema kontrolnoj mreži poligona. U slučaju da je w=-1/16 radi se o linearnoj interpolaciji. U slučaju da vrh označen sa a ima spojnost različitu od šest (izvanredni vrh) nema dovoljno podataka da bi se izračunala nova rubna točka pa je potrebno provesti linearnu interpolaciju što uzrokuje da površina u okolini izvanrednih vrhova nije glatka. Ovaj problem je najveći nedostatak Butterfly sheme. Isti autori stoga 1993. godine predstavljaju modifikaciju Butterfly sheme. Izračunska maska je proširena, u skladu s time dane su i nove težinske vrijednosti. Slijedeća slika prikazuje izgled nove izračunske maske s odgovarajućim težinskim faktorima:
![]()
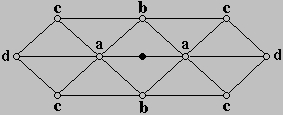
Slika 4. Izračunska maska modificirane Butterfly sheme
Promjenom izgleda izračunske maske još uvijek nije riješen problem glatkoće površine u okolini izvanrednih vrhova, pa je stoga dodano novo pravilo koje riješava taj problem. Slika 5 prikazuje izračunsku masku za slučaj izvanrednog vrha zajedno s težinskim faktorima:
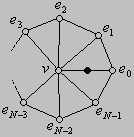
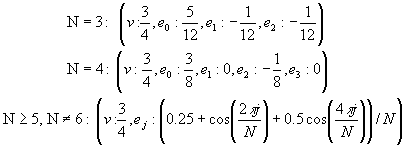
Slika 5. Modificirana Butterfly shema - izračunska maska u slučaju izvanrednog vrha
Sa N je naznačena spojnost vrha v. Vidljivo je da su težinski faktori dani u ovisnosti o spojnosti.
Dobivena površina ima C2 kontinuiranost u regularnim vrhovima (vrhovi spojnosti šest) dok u izvanrednim vrhovima ima C1 kontinuiranost.