PRIMJER RJEŠENJA

     Zbog složenosti jednadžbi i nemogućnosti dobivanja empiričkih podataka eksperimentima za većinu slučajeva, počele su se razvijati numeričke metode rješavanja. Trebalo je malo mašte da bi se uvidjelo da korištenjem računala moguće je proučavati tok fluida lakše i mnogo učinkovitije. Jednom kada je otkrivena moć računala, interes za numeričke metode naglo je porastao. Rješavanje jednadžbi dinamike fluida na računalu je postalo toliko bitno da trenutno je time okupirana trećina istraživača koji rade na tom području, i proporcija još uvijek raste. To područje je poznato kao računalna dinamika fluida (engl. computational fluid dynamics - CFD).

DISKRETIZACIJA

 

     Da bi se navedene jednadžbe (2.1) i (2.2), ili (2.1) i (2.3) za neviskozne fluide, bile rješive na računalu, potrebna je diskretizacija cijelog područja na kojem rješavamo navedene jednadžbe. Pri toj diskretizaciji, prepreke i sredstvo koje okružuje fluid se tretiraju isto kao i fluid, samo sa nekim specijalnim svojstvima koja ostaju konstantna tijekom cijelog izračuna. Za rješavanje postavljenih jednadžbi koristi se već navedena metoda konačnih volumena (FV). Ta metoda dijeli domenu rješenja u konačan broj susjednih kontrolnih volumena - ćelija (engl. voxel ili control volume - CV) raspoređene u fiksnu pravokutnu mrežu poravnate sa Kartezijskim koordinatnim sustavom. Komponente vektora brzine, u u smjeru osi x, v u smjeru osi y i w u smjeru osi z, definirane su u centrima svake stranice ćelije i vezane su lokalno, dok tlak p, i ostale skalarne vrijednosti definiramo u centru svake od ćelija kao što je prikazano na slici 1.

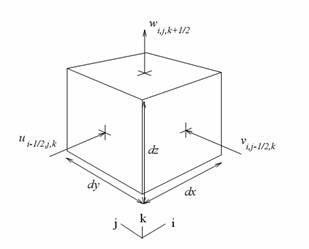
Slika 1. 3D ćelija sa polovičnom notacijom

Koristeći polovičnu indeks notaciju komponente zapisujemo kao:

                    

                     

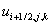
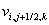
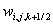
                                                                   (5.1)

 

METODA RJEŠAVANJA SUSTAVA

 

    Rješavanje postavljenih jednadžbi se koristi metodom koju je uveo Stam u svom radu [2]. Kreće se od inicijalnog stanja za t=0:     

                           (5.8)

iz kojeg se dobiva rješenje koje je inicijalno stanje za idući korak. I tako za svaki Δt do kraja simulacije.

Pretpostavlja se da je vektor brzine riješen za vremenski trenutak t, potrebno je pronaći iznos polja za idući vremenski trenutak t+Δt. Postupak kreće od rješenja w₀(x)=u(x,t) prijašnjeg koraka i tada se odvojeno rješava svaki izraz na desnoj strani jednadžbe (4.4). Na slici je naveden tok postupka kada bi se rješavale  Navier-Stokesove jednadžbe. Za jednadžbe ovog problema (Eulerove jednadžbe) izbacujemo treći korak zbog zanemarivanja efekta viskoznosti. Zbog mogućnosti proširenja algoritma i na Navier-Stokesove jednadžbe, biti će opisan i taj korak.

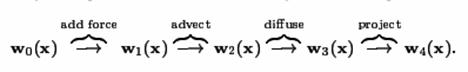
Slika 2. Koraci algoritma

 

            Kao što se na slici vidi, algoritam rješavanja jednadžbi se rastavlja na 4 koraka. Konačno rješenje za vremenski trenutak t+Δt je jednak rezultatu zadnjeg koraka: 

      .  (5.9)

            Simulacija se odvija prolazeći ove korake u svakoj iteraciji. Slijedi detaljniji opis svakog od koraka.

            Postupak počine rješavanjem najlakše rješivog izraza iz jednadžbe očuvanja momenta (4.4), a to je korak dodavanja vanjske sile f. Uz pretpostavku da sila ne varira tijekom vremenskog koraka simulacije, vrijedi:

                      (5.10)

Navedeni izraz (5.10) je dobra aproksimacija sile za interaktivne sustave kroz vremenski korak Δt, jer se sile postavljaju samo na početku svakog vremenskog koraka. U tom koraku uzima se u obzir silu uzgona opisana jednadžbom (4.10), sila definirana metodom ograničavanja vrtložnosti (4.16), te bilo koja druga korisnički definirana sila. S obzirom da su navedene sile definirane u centrima ćelija, brzine se u ovom koraku ažuriraju kao što je navedeno u prijašnjem odlomku u jednadžbama (5.7).

            Idući korak rješava efekt advekcije fluida na samog sebe. Ta pojava se opisuje izrazom -(u)u. Taj izraz čini Navier-Stokesove jednadžbe nelinearnima. Foster i Metaxas u svom radu za rješavanje tog izraza koriste algoritam konačnih razlika. Međutim takav pristup čini njihovu metodu nestabilnom i potrebno je dodatno ograničenje nad veličinom vremenskog koraka. Zbog toga, za male udaljenosti i velike brzine je potreban vrlo mali vremenski korak da bi postupak bio stabilan. Da bi izbjegli takav efekt, u ovoj metodi se koristi potpuno drugačiji pristup koji je uveo Stam [2]. Ta metoda se naziva semi-Lagrangeovom metodom, a temelji se na rješavanju parcijalno diferencijalnih jednadžbi metodom karakteristika. Detaljniji opis metode je već naveden u poglavlju 3.7. Ovdje će se navesti samo bitne karakteristike koje vode do rješenja.

            Za svaki vremenski korak čestice fluida se kreću kroz prostor pod utjecajem brzine samog fluida. Zbog toga, da bi se došlo do vrijednosti brzine u točki  x u novom vremenskom trenutku t+Δt , potrebno je pratiti unatrag točku x kroz polje brzina w₁ kroz vrijeme Δt. To definira putanju p(x,s) koja odgovara djelomičnoj strujnici polja brzine fluida. Nova brzina u točki x je tada postavljena na brzinu koju je čestica, trenutno na poziciji x, imala na svojoj prijašnjoj poziciji prije Δt vremena:

              (5.11) 

            Iz svega navedenog zaključuje se da semi-Lagrangeova metoda gradi novu mrežu praćenjem središnjih točka svake od stranica svih ćelija kroz polje toka brzine. Nove komponente brzina su tada interpolirane u tim točkama i njihove vrijednosti se upisuju na stranice ćelije odakle je krenuo postupak praćenja. Moguće je da točka praćenja  završi u jednom od okupiranih ćelija, tada se jednostavno odbacuje ostatak krivulje koji je izašao izvan domene fluida.

     Ova metoda rješavanja nelinearnog izraza za horizontalno strujanje -(u)u, ima par prednosti. Najvažnija prednost je bezuvjetna stabilnost. Osim toga, iz gore navedene jednadžbe (5.11) vidljivo je da maksimalna vrijednost novog polja nikad nije veća od najveće vrijednosti prijašnjeg polja. Osim toga, ova metoda je vrlo jednostavna za implementiranje. Sve što zahtjeva u praksi je algoritam slijeđenja čestica i linearni interpolator. Jednostavna linearna interpolacija koja je potrebna za ovaj postupak lako se implementira, i u kombinaciji s metodom ograničavanja vrtložnosti daje zadovoljavajuće rezultate. Umjesto jednostavne linearne interpolacije moguće je koristiti i interpolacije viših razina, kao npr. kubična interpolacija. Takve interpolacije daju bolji rezultat, međutim sa sobom donose i određene nedostatke što dovodi do nestabilnosti algoritma. Jednostavnost i stabilnost su dva važna svojstva su poželjna za svaki simulator fluida u računalnoj grafici. Na sličan način simuliramo i strujanje gustoće i temperature kroz fluid.

            Treći korak rješava efekt viskoznosti. Taj efekt je zanemariv za plinovite fluide, ali će svejedno zbog potpunosti biti opisan. Efekt viskoznosti možemo predstaviti difuzijskom jednadžbom:

       (5.12)

Navedena jednadžba je standardna jednadžba za koju su razvijene brojne numeričke metode. Najjednostavniji način rješavanja ove jednadžbe je diskretizirati Laplaceov operator  i tada primijeniti eksplicitni vremenski korak kao u radu Metaxasa i Fostera [3]. Međutim ta metoda je nestabilna za vrlo velike viskoznosti. Zbog toga se preferira uporaba implicitne metode:

                                         (5.13)

gdje je jedinična matrica ili operator identiteta. Kada se operator difuzije diskretizira, ova jednadžba se svodi na slabo popunjeni linearni sustav (engl. sparse linear sistem)  za nepoznato polje w₃. Rješavanje ovog sustava je jednostavno.

            Četvrti korak uključuje korak projekcije, koji služi za dobivanje rezultantnog polja bez divergencije. Kao što je bilo navedeno u poglavlju gdje su postavljene jednadžbe toka, ovaj korak uključuje rješavanje Poissonove jednadžbe koja glasi:

        (5.14)

          (5.15) 

Dakle, korak projekcije zahtjeva dobar Poissonov solver. Zbog utjecaja na preciznost metode karakteristika kojom rješavamo izraz za advekciju, bitno je da polje bude što bliže polju bez divergencije. Još važnije, iz vizualnog gledišta, projekcijski korak prisiljava polje da sadrži vrtložne pojave što rezultira realnijem prikazu plinovitih fluida. Zbog tih uvjeta koristi se što točniji solver za ovaj korak.

            Poissonova jednadžba, kada se diskretizira, postaje također slabo popunjeni linearni sustav jednadžbi koji se može riješiti bilo kojom metodom. U ovom primjeru se koristi Gauss-Seidelova relaksacijska shema koja je također spomenuta u tom poglavlju. Ta metoda se koristi za rješavanje sustava od N dobivenih algebarskih jednadžbi koje možemo zapisati matrično:

            (5.16)

Taj sustav se rješava jedanput po iteraciji algoritma, koristeći rezultate prethodnih koraka po formuli:

            (5.17)

Opisano matričnim računom, Gauss-Seidelova metoda se može izraziti kao:

            , (5.18)

gdje D, L i U su dijagonalna, donja trokutasta i gornja trokutasta matrica matrice A.