Nefotorealistični
prikaz objekta
diplomski rad br. 1819
 FER
FER
4 Prilagodba teksture zakrivljenosti površine
Oblik tijela se, osim crtama obrisa, rubova i pregiba, izvrsno predočava crtama koje prate najveću lokalnu zakrivljenost površine. [2] Na gotovo svakom mjestu na površini tijela moguće je utvrditi smjer najveće zakrivljenosti površine kao tzv. prvi glavni smjer, poznat iz diferencijalne geometrije. Izuzetak su dijelovi kugle, koji su jednako zakrivljeni u svim smjerovima te dijelovi ravnine, koji nisu nimalo zakrivljeni, a tu su i neki posebni slučajevi u kojima je zakrivljenost u nekim (tzv. asimptotskim) smjerovima također nula. Te iznimke treba posebno zbrinuti.
Teksture je dakle potrebno na svakom pojedinom poligonu usmjeriti s njegovim lokalnim prvim glavnim smjerom, čime će potezi iscrtani na njima slijediti slične putove onima koje bi odabrala ljudska ruka u tradicionalnim tehnikama, i tako najbolje ispuniti zadatak prikazivanja oblika tijela.
Osim određivanja smjera u svakom vrhu, bit će zatim potrebno i distribuirati dobivene smjerove na one vrhove pri kojima nije bilo moguće odrediti smjer zbog pogreške. Naposlijetku će se izvesti završno zaglađivanje smjerova.
4.1 Izračunavanje glavnih smjerova općenito
Postoje analitički postupci koji izračunavaju smjerove najveće i najmanje zakrivljenosti u pojedinoj točki na mreži poligona. Oni su svi ovisni prvenstveno o kvaliteti same mreže, kojom se aproksimira željeni oblik, a koji treba "izvući" iz aproksimacije i prikazati linijama. K tome su svi ti postupci u odr. mjeri podložni manjim greškama.
U diferencijalnoj geometriji [3], normalna zakrivljenost Kt plohe u odr. točki T i u odr. smjeru t se definira kao recipročna vrijednost polumjera oskulacijske kružnice koja leži u ravnini s točkom T, normalom plohe i tangentom t i najbolje aproksimira presjek plohe u tom smjeru. Ekstremne vrijednosti zakrivljenosti K1 i K2 nazivamo glavnim zakrivljenostima plohe u točki T, a vektore tangenata pridruženih im krivulja nazivamo glavnim smjerovima u T (dalje označeni kao p1 i p2). Glavni su smjerovi uvijek međusobno okomiti. Tzv. prvi glavni smjer pokazuje smjer najveće zakrivljenosti u točki, dok drugi glavni smjerpokazuje smjer najmanje zakrivljenosti.
Spomenute posebne slučajeve kada je normalna zakrivljenost u točki T jednaka nuli nazivamo asimptotskim smjerovima plohe u točki T.
Na glatkim plohama vrijedi za bilo koji jedinični vektor na nekoj njenoj tangencijalnoj ravnini sljedeća jednakost:
![]()
gdje su komponente x i y vektora izražene u lokalnom ortonormiranom koordinatnom sustavu, a W je tzv. Weingartenova matrica, odn. druga temeljna forma. Za nju je karakteristično da se rotacijom spomenutog lokalnog koordinatnog sistema može dijagonalizirati i dati jednakost:
![]()
gdje su K1 i K2 glavni smjerovi, a x' i y' su sad izraženi pomoću glavnih smjerova kao komponenti.
Ako je X(u, v) lokalna parametrizacija plohe u okolini točke T, možemo koristeći Xu(T), Xv(T) i normalu NT kao lokalni koordinatni sistem izračunati glavne zakrivljenosti i glavne smjerove u točki na sljedeći općenit način. Weingartenova matrica ima oblik:
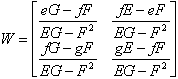
gdje su:
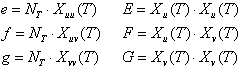
i, u slučaju kad su Xu i Xv ortogonalni, dobivamo simetričnu matricu:
![]()
Ako su λ1 i λ2 vlastite vrijednosti matrice W, slijedi da one odgovaraju glavnim zakrivljenostima K1 i K2, a vlastiti vektori t1 = [t11 t12]T i t2 = [t21 t22]T pridruženi tim vrijednostima su glavni smjerovi plohe u točki T, no izraženi u lokalnim koordinatama. Glavni smjer povezan s većom vlastitom vrijednosti matrice je tzv. prvi glavni smjer i odgovara najvećoj zakrivljenosti, dok drugi glavni smjer pokazuje smjer najmanje zakrivljenosti.
Ti vektori se korištenjem izabrane parametrizacije preslikavaju natrag u euklidski prostor R3 u vektore:
![]()
Time je teorijski određen zadatak izračunavanja glavnih zakrivljenosti, odn. glavnih smjerova na plohi. U konkretnom praktičnom zadatku, prvi korak u izračunavanju glavnih smjerova je odrediti normalu u svakoj točki, a to znači izračunati je u svakom vrhu poligonalne mreže modela. Zatim treba odabrati vektore koji će činiti novi, ortogonalni koordinatni sustav. Zatim se nekim od poznatih postupaka aproksimira matrica W i izračunavaju njeni vlastiti vektori.
Uobičajeni postupci kojima se te vrijednosti izračunavaju mogu se podijeliti u tri skupine, ovisno o tome da li se zasnivaju na aproksimaciji područja analitičkom plohom, računanjem srednje vrijednosti normalnih zakrivljenosti (nakon aproksimacije zakrivljenosti kružnicom u što više smjerova) ili računanjem srednje vrijednosti posebno definiranog tenzora zakrivljenosti. Ovdje je odabran postupak aproksimacije kvadratičnom plohom, s dodatnom posebnom analizom namijenjenom objektima s oštrim bridovima i dijelovima ravnina, kao što su to vrlo česta pravokutna tijela.
4.2 Aproksimacija površine tijela geometrijskom plohom
Zamisao je geometrijsku plohu, odn. polinom, umetnuti u okolinu promatrane točke T i prilagoditi najbližim okolnim točkama, a to su u ovom slučaju susjedni vrhovi na poligonalnoj mreži. (Susjedstvo je određeno kao povezanost točaka nekim od bridova poligona.) Zatim se iz takve plohe mogu izračunati tražene zakrivljenosti, s pretpostavkom da će ona, provučena kroz ostale točke na najbolji način, biti dovoljno slična pravoj plohi da dâ zadovoljavajuće rezultate. Pokazano je da u općem slučaju glatke plohe rezultati konvergiraju k točnim vrijednostima, ako se ne radi o posebnim degeneriranim slučajevima. [4]
Nestabilnost postupka se očituje kad su položaji susjednih vrhova (vrhova uzetih u izračun) smješteni na dva pravca koji se sijeku. Tada se radi o spomenutim asimptotskim smjerovima. Jedan od primjera je dan na slici 4.1.
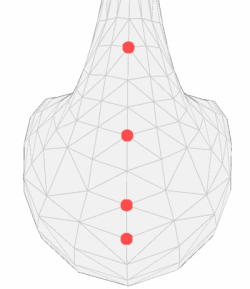
Slika 4.1. Nestabilne točke na primjeru modela patke
Za svaki vrh T na modelu pokušat će se što je bolje moguće prilagoditi kvadratičnu plohu susjednim vrhovima Si. Svaki od njih se preslika u lokalne koordinate (xi, yi, zi), a T postaje (0, 0, 0). Normala NT leži duž pozitivne osi Z, a koristi se, u ovom primjeru, kvadratična ploha određena izrazom:![]()
Neka je W nepoznata Weingartenova matrica izražena u lokalnom koordinatnom sustavu oko vrha T. Za ovakvu plohu matrica W je jednaka:
![]()
Susjedne točke uvode se u matrični sustav jednadžbi:
![]()
gdje je vektor x sastavljen od traženih vrijednosti [A B C]T.
Sustav nema egzaktno rješenje, već mora zadovoljiti polinom u svim uključenim točkama što je bolje moguće. Zato jedino preostaje pronaći najbolje rješenje prema metodi najmanjih kvadrata.
Izračunatim koeficijentima A, B i C određena je dakle kvadratična ploha koja najbolje aproksimira površinu tijela u promatranoj točki. Pripadna Weingartenova matrica, popunjena prema ranije navedenom izrazu, u svojim vlastitim vektorima sadrži traženu aproksimaciju glavnih smjerova u lokalnom koordinatnom sustavu.
Konačne vrijednosti vektora prvog glavnog smjera dobivaju se njegovim preslikavanjem natrag u izvorni koordinatni sustav, a to konkretno znači još samo rotaciju kojom se od smjera vektora normale NT vraćamo na smjer pozitivne osi Z.
4.3 Zaglađivanje smjerova
Pronađene smjerove u vrhovima poželjno je još donekle ujednačiti, da razlika među jednako usmjerenim područjima koja je nastala isključivo zbog nesavršenosti mreže poligona bude što manje očita.
Izračun se izvodi zbrajanjem smjerova među susjednim vrhovima i davanjem prednosti sličnim smjerovima. Pri tom zbrajanju uvažava se posebna aritmetika "dvosmjernih" smjerova, koja suprotne smjerove zbraja kao iste, jer rezultiraju istom orijentacijom tekstura na poligonima.
4.4 Posebnosti kod pravokutnih tijela
Smjer teksture na poligonu koji ima oštar brid (rub ili pregib) ne određuje se pomoću smjerova zakrivljenosti u vrhovima, jer su oni izračunati s pretpostavkom glatke plohe i pretpostavkom postojanja tangencijalnih ravnina u vrhovima. Na oštrim rubovima to zapravo nije ispunjeno te izračunati smjer nema smisla, pa treba prenijeti smjer distribucijom sa susjednih poligona ili, ako to nije moguće, odrediti neovisnim odabirom.
Jedno rješenje koje se u tom slučaju pokazuje estetski prihvatljivim je uzeti smjer okomit na koordinatnu os koja je paralelna s ravninom poligona, odnosno onu os koja je tome najbliža. To je posljedica vrlo čestog običaja da su pravokutni modeli građeni s ravninama paralelnim s koordinatnim osima. Tada se uzima vektorski umnožak normale i dotične osi kao najbolje rješenje za smjer.
Pri iscrtavanju poligona koji imaju oštre bridove, te bridove će se istaknuti uočljivom tamnom crtom kao i obris tijela, zbog sugeriranja oblika tijela na način tipičan za nefotorealistični prikaz. Osim toga, oštrina bridova naglasit će se i pri "sjenčanju", i to posebnim računanjem osvjetljenja. Osvjetljenje se inače računa pojedinačno za svaki vrh poligona; sada ako je utvrđeno da se vrh nalazi na nekom oštrom bridu, osvjetljenje će se računati pomoću normale trokuta, a ne normale koja je bila izvorno izračunata na vrhu s pretpostavkom da se radi o glatkoj plohi.
Na slici 4.2 prikazan je primjer pravokutnog tijela s prikazanim normalama koje su izračunate u vrhovima (plava boja). Umjesto tih normala, za osvjetljenje se koriste se normale poligona (zelena boja). Rezultat je jasan i ispravan dojam oštrog brida na tijelu (desno).
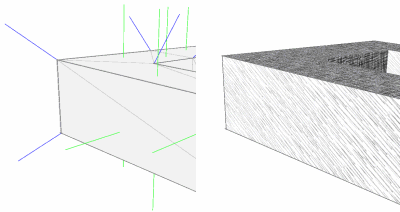
Slika 4.2. Normale trokuta (zeleno) su bolji odabir od normala vrhova (plavo) za osvjetljavanje pravokutnih tijela