|
Simulacija
gibanja krutog tijela slična je simulaciji gibanja čestica. Kod simulacije
čestica stanje čestice određeno je pozicijom 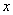 i brzinom
i brzinom 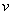 .
Promjena stanja kroz vrijeme određena je promjenom pozicije .
Promjena stanja kroz vrijeme određena je promjenom pozicije 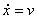 te promjenom brzine
te promjenom brzine 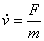 .
Novo stanje odrediti će se pomoću jednog od mnogih postupaka integriranja.
Na sličan način će se simulirati i kruta tijela osim što će stanje
tijela sadržavati više podataka i promjenu stanja će biti nešto
teže za odrediti. .
Novo stanje odrediti će se pomoću jednog od mnogih postupaka integriranja.
Na sličan način će se simulirati i kruta tijela osim što će stanje
tijela sadržavati više podataka i promjenu stanja će biti nešto
teže za odrediti.
Pozicija i orijentacija
Slika
11. Pozicija i orijentacija tijela
Pozicija
čestice u prostoru u vremenu 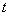 određena je vektorom
određena je vektorom 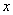 .
Kako kruto tijelo zauzima u prostoru određeni volumen njegov prikaz
je nešto složeniji. Za poziciju tijela uzet će se jedna fiksna točka
u prostoru, pri tome se za tu točku odredi da se u koordinatnom sustavu
tijela nalazi na poziciji .
Kako kruto tijelo zauzima u prostoru određeni volumen njegov prikaz
je nešto složeniji. Za poziciju tijela uzet će se jedna fiksna točka
u prostoru, pri tome se za tu točku odredi da se u koordinatnom sustavu
tijela nalazi na poziciji 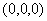 .
Kako bi se pojednostavile mnoge operacije za tu točku se uzima centar
mase tijela. Osim pozicije tijela, za razliku od čestica kruta tijela
se mogu i rotirati tako da je potrebno odrediti njihovu orijentaciju.
Orijentacija tijela se može predstaviti 3x3 matricom rotacije. Tako
da ukoliko je .
Kako bi se pojednostavile mnoge operacije za tu točku se uzima centar
mase tijela. Osim pozicije tijela, za razliku od čestica kruta tijela
se mogu i rotirati tako da je potrebno odrediti njihovu orijentaciju.
Orijentacija tijela se može predstaviti 3x3 matricom rotacije. Tako
da ukoliko je 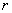 pozicija točke u koordinatnom sustavu tijela pozicija točke u globalnim
koordinatama će biti rezultat rotiranja točke oko ishodišta i zatim
translatiranja točke:
pozicija točke u koordinatnom sustavu tijela pozicija točke u globalnim
koordinatama će biti rezultat rotiranja točke oko ishodišta i zatim
translatiranja točke:
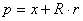 |
(4.1) |
gdje su:
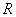 3x3 matrica rotacije
3x3 matrica rotacije
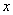 pozicija tijela
pozicija tijela
Prilikom
iscrtavanja tijela koristit će se formula (4.1) za određivanje nove
pozicije svakog vrha tijela. Dakle kod određivanja nove pozicije i
orijentacije tijela prilikom simulacije nije potrebno računati i novu
poziciju svakog vrha tijela već će se to raditi samo prilikom iscrtavanja
budući da postoji grafička podrška za brzo računanje s matricama.
Linearna i kutna brzina
Slika
12. Linearna i kutna brzina tijela
Sljedeće
što je potrebno odrediti je promjena pozicije i orijentacije tijekom
vremena, dakle potrebno je odrediti 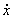 i
i 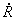 .
Promjena pozicije je jednostavna, budući da je .
Promjena pozicije je jednostavna, budući da je 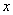 pozicija centra mase u globalnim koordinatama
pozicija centra mase u globalnim koordinatama 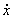 biti će jednako definiranoj linearnoj brzini tijela
biti će jednako definiranoj linearnoj brzini tijela 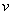 . .
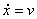 |
(4.2) |
Kutna brzina
može se zapisati pomoću vektora 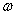 .
Smjer .
Smjer 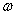 određuje os oko koje se tijelo vrti. Duljina vektora
određuje os oko koje se tijelo vrti. Duljina vektora 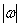 određuje koliko brzo se tijelo vrti (kutna brzina). Za linearnu brzinu
odnos između
određuje koliko brzo se tijelo vrti (kutna brzina). Za linearnu brzinu
odnos između 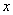 i i 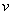 jednak je
jednak je 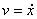 .
Postavlja se pitanje koji je odnos između .
Postavlja se pitanje koji je odnos između 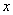 i
i 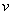 .
Kako stupci od .
Kako stupci od 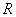 predstavljaju smjerove koordinatnih osi lokalnog sustava tijela, znači
da stupci od
predstavljaju smjerove koordinatnih osi lokalnog sustava tijela, znači
da stupci od 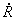 opisuju brzinu promjene smjera koordinatnih osi. Promjena smjera vektora
određena je sa:
opisuju brzinu promjene smjera koordinatnih osi. Promjena smjera vektora
određena je sa:
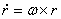 |
(4.3) |
Znamo da
je smjer 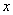 osi lokalnog koordinatnog sustava tijela zapisan u prvom stupcu matrice
osi lokalnog koordinatnog sustava tijela zapisan u prvom stupcu matrice 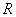 . .
Na isti način se odrede
i ostala dva stupca, te se dobije odnos između 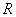 i
i 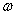 . .
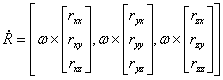 |
(4.4) |
Kako bi se izračun  donekle pojednostavio vektorski produkt ćemo definirati na drugi način.
Vektorski produkt
donekle pojednostavio vektorski produkt ćemo definirati na drugi način.
Vektorski produkt  jednak
je: jednak
je:
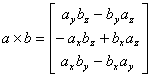 |
(4.5) |
Za određeni vektor 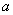 definira se matrica vektorskog produkta kao:
definira se matrica vektorskog produkta kao:
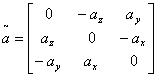 |
(4.6) |
Sada se 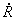 može
zapisati kao: može
zapisati kao:
 |
(4.7) |
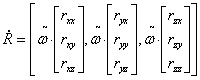
Prema pravilima množenja matrica dobijemo
da je promjena orijentacije jednaka:
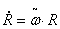 |
(4.8) |
Matrica vektorskog produkta
će se osim za računanje promjene orijentacije dosta često koristiti
kod računanja reakcije na sudar.
Brzina točke na tijelu
Slika
13. Brzina točke na tijelu
Prilikom
rješavanja sudara između tijela često će biti potrebno znati brzinu
određene točke na tijelu. Derivacijom izraza (4.1) i uvrštavanjem
izraza (4.8) te malo raspisivanja dobije se brzina točke na tijelu:
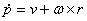 |
(4.9) |
Orijentacija pomoću kvaterniona
Osim 3x3
matrica rotacije orijentacija tijela može se predstaviti i kvaternionima.
Kvaternioni su bolji za prikaz orijentacije zbog mnogih razloga poput
bolje interpolacije između dviju orijentacija. No za simulaciju krutih
tijela glavni razlog za korištenje kvaterniona je zbog greške zaokruživanja
koja se akumulira tijekom rotacije. Konstantnim ažuriranjem orijentacije
pomoću formule (4.8) numerička greška će se nakupiti unutar koeficijenata
matrice tako da matrica rotacije neće više predstavljati isključivo
matricu rotacije već će sadržavati i efekte smika i skaliranja. Greška
se može ispraviti ortonormiranjem matrice prilikom svakog ažuriranja
no bolji način je korištenje kvaterniona. Kako kvaternioni koriste
četiri parametra za prikaz tri stupnja slobode dok matrica koristi
devet parametra očito je da će greška biti mnogo manja. Greška kod
kvaterniona se može zanemariti, no ukoliko je potrebno greška se može
ispraviti normaliziranjem kvaterniona na jediničnu duljinu. Za integriranje
orijentacije će se koristiti kvaternioni dok će matrica rotacije još
uvijek biti potrebna za određene izračune poput računanja momenta
inercije tijela u globalnim koordinatama, također kutna brzina 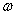 će još uvijek biti prikazana pomoću vektora. Za derivaciju kvaterniona
će još uvijek biti prikazana pomoću vektora. Za derivaciju kvaterniona 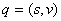 se može pokazati da vrijedi [5]:
se može pokazati da vrijedi [5]:
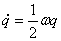 |
(4.10) |
gdje je:
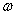 skraćeni zapis za kvaternion
skraćeni zapis za kvaternion 
Za pretvorbu iz kvaterniona 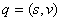 u matricu rotacije
u matricu rotacije 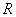 vrijedi
[6]: vrijedi
[6]:
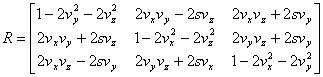 |
(4.11) |
Masa tijela i centar mase
Za realnu
simulaciju krutih tijela potrebno je znati masu tijela i centar mase.
Masa tijela se jednostavno može ručno zadati za svako tijelo, također
centar mase se može intuitivno odrediti za jednostavna tijela poput
kugle ili kocke, međutim za kompleksna konkavna tijela centar će biti
potrebno izračunati.
Iako postoje metode koje računaju svojstva tijela direktno iz mreže trokuta poput [7] kako već imamo izračunato polje udaljenosti svojstva tijela se mogu izračunati na jednostavniji način slično kao u [8].
Masa tijela 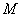 i
centar mase i
centar mase 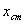 mogu se izračunati pomoću zadane gustoće tijela
mogu se izračunati pomoću zadane gustoće tijela 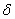 .
Za ukupnu masa tijela vrijedi: .
Za ukupnu masa tijela vrijedi:
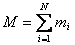 |
(4.12) |
gdje je:
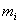 masa pojedine čestice tijela
masa pojedine čestice tijela
Kako za tijelo
imamo izračunato polje udaljenosti masa tijela će se izračunati zbrajanjem
masa pojedinih ćelija unutar polja udaljenosti, s time da se zbrajaju
samo one ćelije koje se nalaze unutar tijela. Vrijedi:
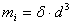 |
(4.13) |
gdje je:
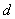 duljina
stranice ćelije duljina
stranice ćelije
Centar mase može izračunati prema sljedećoj
formuli:
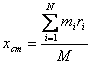 |
(4.14) |
gdje je:
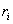 udaljenost centra pojedine ćelije od ishodišta koordinatnog sustava
udaljenost centra pojedine ćelije od ishodišta koordinatnog sustava
Moment inercije
Kao što
masa tijela utječe na translaciju tijela moment inercije (moment tromosti)
utječe na rotaciju tijela. Da bi ispravno odredili kutnu brzinu tijela
prilikom određivanja reakcije na sudar potrebno je odrediti moment
inercije tijela. Kao i centar mase moment inercije se ne može intuitivno
odrediti te ga je potrebno izračunati. Za inerciju materijalne točke
vrijedi:
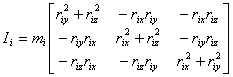 |
(4.15) |
gdje je:
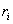 udaljenost točke od centra rotacije
udaljenost točke od centra rotacije
Na sličan način kao
što se masa tijela računa zbrajanjem mase ćelija koje se nalaze unutar
tijela tako će se i moment inercije izračunati zbrajanjem momenta
inercije pojedinih ćelija. Ćelije su oblika kocke pa je potrebno odrediti
moment inercije kocke. Za moment inercije kocke vrijedi:
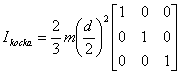 |
(4.16) |
gdje su:
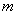 masa kocke
masa kocke
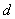 duljina stranice kocke
duljina stranice kocke
Može se pokazati da
je moment inercije tijela oko zadane točke jednak zbroju momenta inercije
oko težišta i momenta inercije čestice oko zadane točke. Slijedi
da je moment inercije tijela 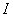 jednak:
jednak:
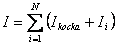 |
(4.17) |
Na prvi pogled pomislilo
bi se da je potrebno računati prethodnu sumu svaki put kod promjene
rotacije objekta. To bi bilo računski prezahtjevno tako da će se moment
inercije izračunati samo jedanput na početku programa dok tijelo još
nije rotirano a ispravan moment inercije će se prilikom svake promjene
orijentacije računati prema sljedećoj formuli [5]:
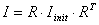 |
(4.18) |
gdje su:
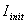 početni moment inercije tijela
početni moment inercije tijela
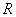 3x3 matrica orijentacije
3x3 matrica orijentacije
U programu će se zbog
brzine spremati inverzija momenta inercije pa se u tom slučaju moment
inercije može izračunati na sljedeći način [5]:
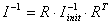 |
(4.19) |
|


