|
Kruta tijela
se na računalu najčešće prikazuju pomoću mreže trokuta. Za svako
tijelo definirati će se lista vrhova, trokuta i bridova. Većina programskih
alata za modeliranje podržava zapis objekta kao mreže poligona pri
čemu se u datoteku zapisuju liste vrhove i trokuta, međutim bez liste
bridova. Budući da će za detekciju sudara konkavnih tijela biti potrebno
znati i pojedine bridove svakog tijela potrebno je posebno izračunati
i bridove. Bridovi se odrede tako da se za svaki trokut u listi traži
ima li neki drugi trokut dva vrha koji se podudaraju s vrhovima prvog
trokuta. Osim toga mnogi programski alati pri zapisu liste vrhova iste
vrhove zapisuju više puta za različite trokute, tako da je često
potrebno izbaciti duple vrhove.
Polje udaljenosti
Osim mreže
trokuta za svako tijelo definirat će se i polje udaljenosti. Polje
udaljenosti za svaku točku u prostoru određuje udaljenost te točke
od tijela. Ovisno o kompleksnosti tijela biti će potrebna različita
veličina polja. Polje se može spremiti na jednoliku mrežu ili na
oktalno stablo, ovisno o tome što je usko grlo u simulaciji, memorija
ili procesor. Budući da će se u ovoj simulaciji simulirati uglavnom
maleni objekti memorija neće biti usko grlo pa će se koristiti jednolika
mreža.
Slika
1. 2D polje udaljenosti za simbol R [2]
Polje udaljenosti
definirat će se samo unutar omeđujućeg volumena tijela poravnatog
s koordinatnim osima (AABB Axis aligned bounding box). Za svaku točku
mreže unutar AABB potrebno je odrediti udaljenost te točke od površine
tijela. Pri tome je potrebno odrediti je li točka unutar tijela ili
izvan, za točke unutar tijela udaljenost će se označiti negativnom
vrijednošću a za točke izvan tijela udaljenost će imati pozitivnu
vrijednost. Određivanje udaljenosti detaljnije je objašnjeno u poglavlju
o detekciji sudara. Udaljenost određene točke (x y z) od tijela
odredit će se trilinearnom interpolacijom 8 najbližih susjednih točaka,
pri čemu je koordinate x, y, z potrebno transformirati u
koordinatni sustavu ćelije i normalizirati na vrijednost [0 1].
Slika 2. Interpolacija udaljenosti
Udaljenost je određena sljedećom formulom:
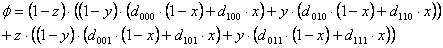 |
(2.1) |
Velika prednost korištenja
polja udaljenosti je pri računanju normale. Kako točke unutar tijela
imaju negativnu, a točke izvana pozitivnu vrijednost normala se može
definirati kao gradijent udaljenosti u traženoj točki:
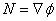 |
(2.2) |
Time dobivamo aproksimaciju
normale u cijelom prostoru za razliku od normale definirane na samoj
površini objekta čime se ubrzava postupak detekcije sudara i određivanja
reakcije na sudar.
Gradijent skalarnog polja
je vektorsko polje koje pokazuje u kojem smjeru najviše raste skalarno
polje i njegova veličina odgovara povećanju u tom smjeru. Gradijent
se definira kao:
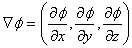 |
(2.3) |
Slika
3.Skalarno polje i njemu odgovarajuće vektorsko polje
Potrebno
je izračunati parcijalne derivacije udaljenosti u smjerovima x, y, z.
Kao i kod određivanja udaljenosti normala će se također odrediti
interpolacijom. Parcijalna derivacija 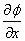 odredi se tako da se prvo izračunaju parcijalne derivacije točaka
koje se nalaze u sredini bridova paralelnih sa x.
odredi se tako da se prvo izračunaju parcijalne derivacije točaka
koje se nalaze u sredini bridova paralelnih sa x.
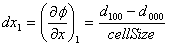 |
(2.4) |
gdje je:
cellSize, duljina stranice kocke ćelije
S time da valja napomenuti
da prilikom implementacije nije potrebno dijeliti sa cellSize jer
nas ne zanima točna veličina gradijenta već samo smjer. Ukupna derivacija
po x izračuna se bilinearnom interpolacijom između četiri brida.
Slika 4. Interpolacija normale
Vrijednost x normale sudara je:
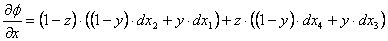 |
(2.5) |
Na sličan način se
odrede i preostale parcijalne derivacije: 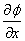 i
i 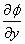 koje određuju normalu
koje određuju normalu 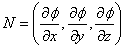 . .
Određivanje ćelije u kojoj se nalazi točka te koordinate točke u koordinatnom sustavu ćelije prikazano je na sljedećoj slici:
Slika
5. 2D prikaz određivanja ćelije u kojoj se nalazi točka te njezine koordinate u koordinatnom sustavu ćelije
Formula za određivanje indeksa prve točke ćelije 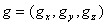 u kojoj se nalazi točka je: u kojoj se nalazi točka je:
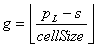 |
(2.6) |
gdje su:
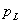 koordinate točke u lokalnom sustavu tijela koordinate točke u lokalnom sustavu tijela
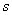 koordinate prve točke mreže u lokalnom sustavu tijela koordinate prve točke mreže u lokalnom sustavu tijela
Koordinate točke u lokalnom koordinatnom sustavu ćelije 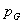 odrede se prema sljedećoj formuli: odrede se prema sljedećoj formuli:
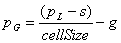 |
(2.7) |
|


