|
Kao
što su se impulsi koristili za modeliranje sudara i kontakata na sličan
način možemo odrediti impulse za modeliranje zglobova tj. za određivanje
ograničenja pozicije i orijentacije. Postoje dvije osnovne vrste zglobova:
translacijski i rotacijski zglobovi.
Translacijski zglobovi
Translacijski
zglobovi brišu translacijske stupnjeve slobode, to znači da se tijela
neće moći translatirati u određenim smjerovima ali će se moći rotirati
u svim smjerovima.
Slika
21. Stupnjevi slobode translacijskih zglobova
Translacijski zglob s ograničena tri stupnja slobode
Najjednostavniji
primjer zgloba je sferni zglob koji se vidi na slici 21a. Zglob spaja
jednu točku tijela A s jednom točkom tijela B tako da se tijela jedino
mogu rotirati oko zajedničke spojne točke. Ovaj zglob briše sva tri
translacijska stupnja slobode. Naravno da se tijela mogu translatirati
u globalnom sustavu, međutim u odnosu jedan na prema drugom tijela
se ne mogu translatirati.
Slika
22. Sferni zglob
Ako bi se tijela simulirala
bez uzimanja u obzir ograničenja, tijela će se razdvojiti kao na slici
22. Potrebno je pronaći impuls 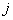 na početku simulacijskog koraka kojim će se eliminirati udaljenost
na početku simulacijskog koraka kojim će se eliminirati udaljenost 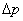 koja nastaje na kraju simulacijskog koraka (stabilizacija pozicije).
Udaljenost na kraju vremenskog koraka jednaka je:
koja nastaje na kraju simulacijskog koraka (stabilizacija pozicije).
Udaljenost na kraju vremenskog koraka jednaka je:
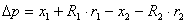 |
(9.1) |
gdje su:
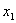 , ,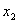 pozicije tijela na kraju vremenskog koraka
pozicije tijela na kraju vremenskog koraka
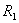 , ,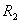 orijentacije tijela na kraju vremenskog koraka
orijentacije tijela na kraju vremenskog koraka
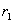 , ,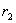 pozicije točke zgloba u lokalnim koordinatama tijela
pozicije točke zgloba u lokalnim koordinatama tijela
Budući da točke na
tijelu uglavnom imaju nelinearno gibanje odgovarajući impuls se može
odrediti rješavanjem nelinearne jednadžbe iterativno kao u [12] no
ovdje će se odrediti na pojednostavljen način kao u [13]. Ako je relativna
brzina između dvije točke u simulacijskom koraku promijenjena za 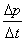 kao da je relativno gibanje između točaka linearno tada će izračunati
impuls
kao da je relativno gibanje između točaka linearno tada će izračunati
impuls 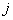 kojim se eliminira brzina
kojim se eliminira brzina 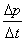 smanjiti udaljenost
smanjiti udaljenost 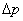 no neće se potpuno eliminirati. Stoga je potrebno iterativno nekoliko
puta izračunati impuls
no neće se potpuno eliminirati. Stoga je potrebno iterativno nekoliko
puta izračunati impuls 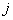 sve dok udaljenost ne nestane s određenom tolerancijom. U [13] su odredili
da je za vremenski korak od 0.04s koji odgovara simulaciji od 25 sličica
u sekundi dovoljno jedna do dvije iteracije da bi se eliminirala udaljenost
s tolerancijom od 10-6m, osim u slučajevima gdje tijela
imaju veliku brzinu. U primjerima napravljenim u ovom radu dovoljna
je bila i jedna iteracija za uvjerljivu simulaciju. Prednost ovakvog
pojednostavljenja je da je jednadžba za određivanje odgovarajućeg
impulsa linearna pa je impuls lako za izračunati.
sve dok udaljenost ne nestane s određenom tolerancijom. U [13] su odredili
da je za vremenski korak od 0.04s koji odgovara simulaciji od 25 sličica
u sekundi dovoljno jedna do dvije iteracije da bi se eliminirala udaljenost
s tolerancijom od 10-6m, osim u slučajevima gdje tijela
imaju veliku brzinu. U primjerima napravljenim u ovom radu dovoljna
je bila i jedna iteracija za uvjerljivu simulaciju. Prednost ovakvog
pojednostavljenja je da je jednadžba za određivanje odgovarajućeg
impulsa linearna pa je impuls lako za izračunati.
Iz (7.12) slijedi da za impuls kojim
se eliminira brzina 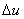 vrijedi: vrijedi:
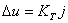 |
(9.2) |
Iz čega se slijedi da za impuls kojim
se eliminira udaljenost 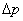 na kraju vremenskog koraka vrijedi:
na kraju vremenskog koraka vrijedi:
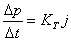 |
(9.3) |
gdje je:
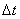 veličina vremenskog koraka
veličina vremenskog koraka
Nakon završetka simulacijskog
koraka potrebno je još zadovoljiti ograničenja brzine (stabilizacija
brzine). Relativna brzina točaka tijela koje odgovaraju zglobu mora
biti jednaka nuli tako da je potrebno eliminirati brzinu na kraju simulacijskog
koraka. Brzina na kraju simulacijskog koraka jednaka je:
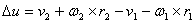 |
(9.4) |
gdje su:
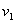 , ,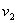 brzine tijela na kraju vremenskog koraka
brzine tijela na kraju vremenskog koraka
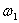 , ,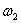 kutne brzine tijela na kraju vremenskog koraka
kutne brzine tijela na kraju vremenskog koraka
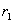 , ,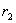 pozicije točke zgloba u lokalnim koordinatama tijela
pozicije točke zgloba u lokalnim koordinatama tijela
Impuls kojim se eliminira
brzina 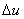 određen
je jednadžbom (9.2). određen
je jednadžbom (9.2).
Translacijski zglob s ograničena dva stupnja slobode
Druga vrsta
translacijskog zgloba je zglob koji briše dva stupnja slobode i prikazan
je na slici 21b. Zglob je određen točkama zgloba 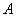 i
i 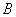 u lokalnim koordinatama prvog i drugog tijela i vektora osi rotacije
u lokalnim koordinatama prvog i drugog tijela i vektora osi rotacije 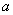 u lokalnim koordinatama prvog tijela. Točka
u lokalnim koordinatama prvog tijela. Točka 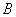 može se slobodno gibati na liniji
može se slobodno gibati na liniji 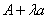 .
Prije računanja impulsa točka .
Prije računanja impulsa točka 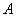 trebala bi se pomaknuti po liniji određenoj s osi
trebala bi se pomaknuti po liniji određenoj s osi 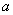 na poziciju gdje je najmanja udaljenost od točke
na poziciju gdje je najmanja udaljenost od točke 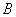 .
Prilikom implementacije točka se neće direktno pomicati po liniji
nego će se impuls izračunati na drugi način. Impuls kojim se eliminira
promjena brzine .
Prilikom implementacije točka se neće direktno pomicati po liniji
nego će se impuls izračunati na drugi način. Impuls kojim se eliminira
promjena brzine 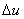 određen je jednadžbom (9.3). Impuls se izračuna projekcijom jednadžbe
(9.3) u dvodimenzionalni prostor. Potrebno je odrediti linearno nezavisne
vektore
određen je jednadžbom (9.3). Impuls se izračuna projekcijom jednadžbe
(9.3) u dvodimenzionalni prostor. Potrebno je odrediti linearno nezavisne
vektore 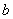 i
i 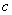 okomite na vektor
okomite na vektor 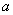 .
Vektor .
Vektor 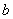 izračuna se pomoću vektorskog produkta vektora
izračuna se pomoću vektorskog produkta vektora 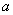 i vektora jedne od osi koordinatnog sustava, na primjer
i vektora jedne od osi koordinatnog sustava, na primjer 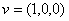 .
Problem je što vektorski produkt između dva paralelna vektora nije
definiran pa ukoliko je kut između .
Problem je što vektorski produkt između dva paralelna vektora nije
definiran pa ukoliko je kut između 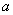 i
i 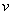 približno jednak nuli vektor
približno jednak nuli vektor 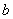 se izračuna kao vektorski produkt vektora
se izračuna kao vektorski produkt vektora 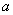 i vektora neke druge osi npr.
i vektora neke druge osi npr. 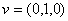 .
Za uvjet kuta se uzima vrijednost približno jednaka nula a ne jednaka
nuli zbog bolje preciznosti prilikom računanja okomitog vektora. Vektor .
Za uvjet kuta se uzima vrijednost približno jednaka nula a ne jednaka
nuli zbog bolje preciznosti prilikom računanja okomitog vektora. Vektor 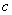 jednak je vektorskom produktu vektora
jednak je vektorskom produktu vektora 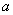 i
i 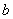 .
Izračunati vektori .
Izračunati vektori 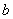 i
i 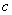 odgovaraju stupnjevima slobode koje treba ograničiti. Slijedi da za
jednadžbu pomoću koje se računa impuls vrijedi:
odgovaraju stupnjevima slobode koje treba ograničiti. Slijedi da za
jednadžbu pomoću koje se računa impuls vrijedi:
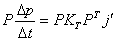 |
(9.5) |
gdje su:
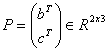 matrica projekcije
matrica projekcije
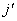 projicirani impuls u dvije dimenzije
projicirani impuls u dvije dimenzije
Impuls u tri dimenzije određen je sa:
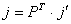 |
(9.6) |
Na isti način se odredi i impuls kojim
se eliminira promjena brzine 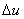
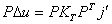 |
(9.7) |
Također je potrebno impuls 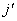 pomoću izraza (9.6) transformirati u 3D prostor.
pomoću izraza (9.6) transformirati u 3D prostor.
Translacijski zglob s ograničenim jednim stupnjem slobode
Ovaj translacijski
zglob briše samo jedan stupanj slobode i prikazan je na slici 21c.
Zglob je određen točkama zgloba 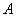 i
i 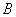 u lokalnim koordinatama prvog i drugog tijela i vektora osi rotacije
u lokalnim koordinatama prvog i drugog tijela i vektora osi rotacije 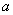 i
i 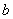 u lokalnim koordinatama prvog tijela. Točka
u lokalnim koordinatama prvog tijela. Točka 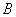 može se slobodno gibati na ravnini
može se slobodno gibati na ravnini 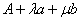 .
Potrebno je prije računanja impulsa pomaknuti točku .
Potrebno je prije računanja impulsa pomaknuti točku 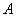 po ravnini na poziciju gdje je najmanje udaljena od točke
po ravnini na poziciju gdje je najmanje udaljena od točke 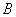 .
Dakle, impuls će se izračunati projekcijom jednadžbi (9.2) i (9.3)
u jednodimenzionalni prostor. Matrica projekcije jednaka je .
Dakle, impuls će se izračunati projekcijom jednadžbi (9.2) i (9.3)
u jednodimenzionalni prostor. Matrica projekcije jednaka je 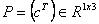 a impulsi kojima se eliminira promjena udaljenosti
a impulsi kojima se eliminira promjena udaljenosti 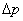 i brzine
i brzine 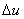 računaju se rješavanjem jednadžbi na isti način kao i u prethodnom
poglavlju. I zglob sa sva tri ograničena stupnja slobode bi se također
mogao riješiti na isti način s time da se za matricu projekcije uzme
jedinična matrica.
računaju se rješavanjem jednadžbi na isti način kao i u prethodnom
poglavlju. I zglob sa sva tri ograničena stupnja slobode bi se također
mogao riješiti na isti način s time da se za matricu projekcije uzme
jedinična matrica.
Rotacijski zglobovi
Rotacijski
zglobovi brišu jedan do tri rotacijska stupnja slobode. Za razliku
od prijašnjih impulsa ovdje će biti potrebno izračunati kutni impuls 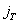 .
Kutni impuls mijenja samo kutnu brzinu. Iz (7.18) se može vidjeti da
promjena kutne brzine pod utjecajem kutnog impulsa iznosi: .
Kutni impuls mijenja samo kutnu brzinu. Iz (7.18) se može vidjeti da
promjena kutne brzine pod utjecajem kutnog impulsa iznosi:
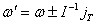 |
(9.8) |
Sada se može izračunati
kutni impuls iz relativne promjene brzine:
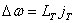 |
(9.9) |
gdje je:
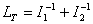
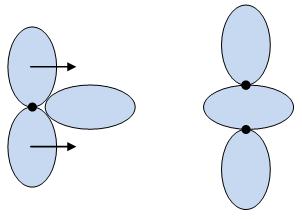
Slika
23. Stupnjevi slobode rotacijskih zglobova
Rotacijski zglob s ograničena tri stupnja slobode
Za zglob
koji briše sva tri rotacijska stupnja slobode vrijedi da se mogu translatirati
u svim smjerovima ali se ne mogu rotirati relativno u donosu jedan na
prema drugom, prikazan je na slici 23a. Slično kao što je kod translacijskog
zgloba bilo potrebno eliminirati udaljenost na kraju simulacijskog koraka
tako je ovdje potrebno eliminirati rotaciju koja nastaje na kraju simulacijskog
koraka. Promjena u relativnoj orijentaciji između tijela na kraju simulacijskog
koraka jednaka je:
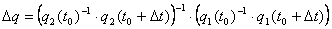 |
(9.10) |
gdje su:
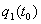 , , 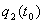 orijentacije tijela na početku simulacijskog koraka
orijentacije tijela na početku simulacijskog koraka
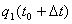 , , 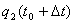 orijentacije tijela na kraju simulacijskog koraka
orijentacije tijela na kraju simulacijskog koraka
Kvaternion 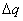 potrebno je pretvoriti u os rotacije
potrebno je pretvoriti u os rotacije 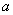 i kut rotacije
i kut rotacije 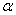 .
Rotacija koju je potrebno eliminirati jednaka je .
Rotacija koju je potrebno eliminirati jednaka je 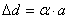 .
Iz (9.9) slijedi da za kutni impuls kojim se eliminira rotacija .
Iz (9.9) slijedi da za kutni impuls kojim se eliminira rotacija 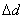 vrijedi:
vrijedi:
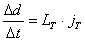 |
(9.11) |
Odgovarajući impuls 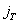 se računa iterativno sve dok rotacija
se računa iterativno sve dok rotacija 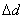 ne nestane s odgovarajućom tolerancijom. Na kraju simulacijskog koraka
mora se eliminirati i razlika u relativnoj kutnoj brzini između tijela
ne nestane s odgovarajućom tolerancijom. Na kraju simulacijskog koraka
mora se eliminirati i razlika u relativnoj kutnoj brzini između tijela 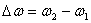 .
Za impuls kojim se eliminira kutna brzina .
Za impuls kojim se eliminira kutna brzina 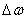 vrijedi:
vrijedi:
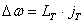 |
(9.12) |
Rotacijski zglob s ograničena dva stupnja slobode
Rotacijski
zglob koji briše dva rotacijska slobode stupnja prikazan je na
slici 23b. Tijela se mogu rotirati oko jedne zajedničke osi i translatirati
u svim smjerovima. Zglob je određen s dvije osi 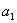 i
i 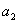 koje predstavljaju tu zajedničku os u lokalnim koordinatama tijela.
Potrebno je odrediti linearno nezavisne vektore
koje predstavljaju tu zajedničku os u lokalnim koordinatama tijela.
Potrebno je odrediti linearno nezavisne vektore 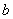 i
i 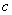 okomite na vektor
okomite na vektor 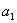 .
Vektori se odrede na isti način kako je opisano u poglavlju o translacijskim
zglobovima. Greška koja nastaje prilikom simulacije tj. razlika u orijentaciji
na kraju simulacijskog koraka koju treba ispraviti jednaka je vektorskom
produktu dviju rotacijskih osi u trenutku .
Vektori se odrede na isti način kako je opisano u poglavlju o translacijskim
zglobovima. Greška koja nastaje prilikom simulacije tj. razlika u orijentaciji
na kraju simulacijskog koraka koju treba ispraviti jednaka je vektorskom
produktu dviju rotacijskih osi u trenutku 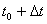 . .
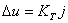 |
(9.13) |
Odgovarajući impuls
izračunat će se projekcijom jednadžbe (9.11) u ravninu određenu
sa vektorima b
i c. Dakle, vrijedi:
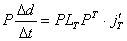 |
(9.14) |
gdje su:
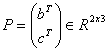 matrica projekcije
matrica projekcije
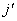 projicirani impuls u dvije dimenzije
projicirani impuls u dvije dimenzije
Za kutni impuls kojim
se eliminira razlika u kutnim brzinama 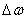 vrijedi:
vrijedi:
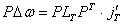 |
(9.15) |
Kutni impuls u tri dimenzije
jednak je 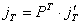 . .
Rotacijski zglob s ograničenim jednim stupnjem slobode
Rotacijski
zglob s ograničenim samo jednim rotacijskim stupnjem slobode prikazan
je na slici 23c. Tijela se mogu translatirati u svim smjerovima i rotirati
oko dva linearno nezavisna vektora 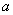 i
i 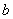 .
Zglob je određen s dva vektora .
Zglob je određen s dva vektora 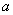 i
i 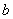 pri čemu se
pri čemu se 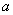 nalazi u lokalnom koordinatnom sustavu tijela prvog tijela dok se
nalazi u lokalnom koordinatnom sustavu tijela prvog tijela dok se 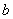 nalazi u lokalnom koordinatnom sustavu drugog tijela. Oba dva vektora
su normalizirana. Zglob onemogućava rotiranje oko osi
nalazi u lokalnom koordinatnom sustavu drugog tijela. Oba dva vektora
su normalizirana. Zglob onemogućava rotiranje oko osi 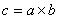 ,
to znači da kut između vektora ,
to znači da kut između vektora 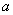 i
i 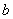 . . 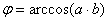 mora biti jednak tokom cijele simulacije. Greška koja nastaje na kraju
simulacijskog koraka tj. razlika u rotaciji koju treba eliminirati jednaka
je:
mora biti jednak tokom cijele simulacije. Greška koja nastaje na kraju
simulacijskog koraka tj. razlika u rotaciji koju treba eliminirati jednaka
je:
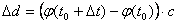 |
(9.16) |
Kutni impuls kojim se
eliminira nastala greška računa se projekcijom jednadžbe (9.11) u
jednodimenzionalni prostor. Matrica projekcije jednaka je 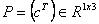 .
Razlika u kutnim brzinama .
Razlika u kutnim brzinama 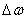 eliminira se projekcijom jednadžbe (9.12) s istom matricom projekcije.
Svi rotacijski zglobovi se mogu simulirati pomoću jednadžbi (9.11)
i (9.12) s time da se za rotacijski zglob s ograničena tri stupnja
slobode koristi jedinična matrica za matricu projekcije.
eliminira se projekcijom jednadžbe (9.12) s istom matricom projekcije.
Svi rotacijski zglobovi se mogu simulirati pomoću jednadžbi (9.11)
i (9.12) s time da se za rotacijski zglob s ograničena tri stupnja
slobode koristi jedinična matrica za matricu projekcije.
Hibridni model
Prednost
prethodne metode modeliranja zglobova je što se može jednostavno integrirati
u simulaciju sa sudarima i kontaktima. Korak integracije je sada:
- detekcija i rješavanje sudara
i stabilizacija brzine
- određivanje novih brzina
i stabilizacija brzine
- detekcija i rješavanje kontakata
i stabilizacija pozicije
- određivanje novih pozicija
i stabilizacija brzine
Budući da
se prilikom rješavanja sudara i određivanja novih brzina pod utjecajem
gravitacije mijenjaju brzine potrebno je izvršiti stabilizaciju brzine
nakon tih koraka. Stabilizacija pozicije je povezana s rješavanjem
kontakata. Nakon konstruiranja kontaktnog grafa rješavaju se kontakti
jedan po jedan od najniže prema najvišoj razini. Nakon rješavanja
svih kontakata između tijela na određenoj razini s tijelima na nižoj
razini rješavaju se ograničenja (zglobovi) između tijela na toj razini
i tijela na nižoj razini. Također se izvodi i propagiranje šoka na
isti način. Na kraju se odrede nove pozicije i orijentacije i ponovo
se izvede stabilizacija brzine. Razlog zbog kojeg se stabilizacija pozicije
vrši unaprijed je zbog toga jer ako bi se stabilizacije izvela nakon
određivanja novih pozicija došlo bi do preklapanja objekata. Na sljedećoj
slici se vidi slučaj kada se ne koristi stabilizacija unaprijed. Tijela
na slici lijevo bi došla u konfiguraciju prikazanu desno i tada bi
se pokušalo spojiti točke zgloba, što je nemoguće bez preklapanja
tijela. Korištenjem stabilizacije unaprijed onemogućuje se uopće
dolazak u desnu konfiguraciju [12].
 Slika 24. Stabilizacija unaprijed
|


