Završni rad br. 38

Da bismo mogli formalno opisati propagaciju svjetlosti kroz prostor, i time izgraditi teorijski model osvjetljenja pogodan za računalnu simulaciju, potrebno je prvo sagledati i točno definirati pojam svjetlosti,  način propagacije svjelosti, te sve pojave i učinke koji se pritom javljaju. Postoji više interpretacija, razvijanih tokom stoljeća. Najjednostavnije shvaćanje svjetlosti jest u okviru geometrijske optike. Svjetlost se predstavlja skupom svjetlosnih zraka – diskretnih, apstraktnih objekata bez mase i dimenzija. S druge strane, u okviru fizikalne optike, svjetlost je shvaćena kao elektromagnetsko zračenje, te se sukladno tome, širenje svjetlosti shvaća kao širenje vala. Svjetlosne 'zrake' su tada ništa drugo doli aproksimacija valnih fronta svjetlosti. Treće shvaćanje svjetlosti dolazi iz kvantne fizike, a ono kaže da je svjetlost skup elementarnih čestica, 'paketića' energije, zvanih fotoni. Trenutno najpotpuniji model svjetlosti jest kombinacija valne i čestične interpretacije prirode svjetlosti. Neovisno o modelu interpretacije, svjetlost pokazuje određena svojstva i učinke koji se javljaju prilikom njena gibanja. Najosnovnija svojstva su refleksija i refrakcija.

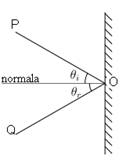
Refleksija se definira kao promjena smjera širenja svjetlosne zrake (tj. vala), na granici dvaju sredstava. Ovo je najučestaliji primjer optičkih efekata – svjetlost putuje zrakom, doseže površinu nekog objekta, te se odbija, mijenjajući smjer svog širenja. Matematički, ta se promjena smjera opisuje pomoću dviju veličina – upadnog kuta, i kuta refleksije. Ti se kutevi definiraju s obzirom na normalu površine na koju svjetlost upada. Zakon refleksije jednostavno kaže: upadni kut je jednak kutu refleksije (Slika 2).

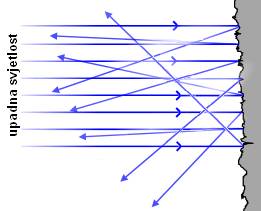
Međutim, valja imati na umu da većina realnih tijela imaju površine koje nisu savršeno glatke. To znači da će normale na površinu biti različite za pojedine upadne zrake svjetlosti, a to nadalje znači i da će kutevi refleksija biti različiti za pojedine zrake, makar sve imaju iste upadne kuteve s obzirom na ravninu površine tijela. Drugim riječima, na grubim površinama će reflektirane zrake biti raspršene u različitim smjerovima (Slika 3). Iz tog razloga, možemo reći da postoje dvije različite vrste refleksija: zrcalna refleksija, i difuzna refleksija. Kod idealno zrcalne refleksije, savršeno glatko tijelo reflektira sve zrake u istom smjeru, dok kod idealno difuzne refleksije, savršeno difuzno tijelo reflektira zrake svjetlosti jednoliko u svim smjerovima, čineći da se svjetlost širi iznad tijela u obliku polukugle. Primjer gotovo idealne zrcalne refleksije su ogledala, dok bi primjer difuzne refleksije bilo neobrađeno drvo. Dakako, svi realni predmeti pokazuju obje komponente refleksije, ali u različitim omjerima.

Vezano uz refleksiju, valja spomenuti još i učinak pretapanja boja. Naime, ukoliko se dva predmeta nalaze blizu jedan drugoga, očito je da se može dogoditi da zrake svjetlosti reflektirane od jednog predmeta upadnu na drugi. U slučaju zrcalne refleksije, cjelokupna slika predmeta će biti reflektirana prema drugom predmetu (primjerice, ako postavimo dva ogledala jedno pored drugog, vidjet ćemo u njima sliku u slici u slici, u beskonačnost). No, u slučaju difuzne refleksije, efekt je mnogo suptilniji. Budući da nema jasne, usmjerene slike, nego samo širok prostor razasutih zraka, ti će predmeti utjecati jedan na drugoga samo blagom promjenom percipirane boje. Primjerice, ako pored izvora bijele svjetlosti stavimo bijeli papir, te mu približimo jarko crveni predmet (poput crvenog flomastera), papir će na jednom dijelu poprimiti blago crvenkastu boju. Ovaj se efekt naziva pretapanje boja.

Sljedeće osnovno svojstvo koje pokazuje svjetlost jest refrakcija. To je pojava koja se javlja kad svjetlost prelazi iz jednog propagacijskog sredstva u drugo, i time mijenja brzinu. Naime, za svako sredstvo se može definirati tzv. indeks loma, koji govori koliko će dano sredstvo usporiti gibanje svjetlosti. Dakle, indeks loma se definira na sljedeći način:

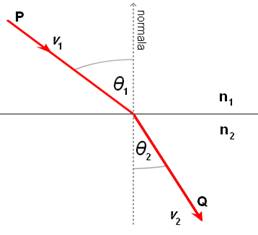
Zakon refrakcije kaže da će se zbog promjene brzine gibanja svjetlosti, promijeniti i njen smjer širenja. Ukoliko definiramo upadni kut i kut refleksije s obzirom na normalu granice između dvaju sredstava, onda će vrijediti da se sinus upadnog kuta prema sinusu kuta refrakcije odnosi kao upadna brzina svjetlosti prema izlaznoj brzini. Ukoliko upadnu i izlaznu brzinu izrazimo pomoću indeksa loma, zakon refrakcije možemo formulirati ovako:

Međutim, treba imati na umu da u većini realnih situacija, upadna zraka svjetlosti neće biti isključivo reflektirana, niti isključivo refraktirana, već će se dogoditi obje pojave. Totalna refleksija i totalna refrakcija su moguće samo u nekim posebnim slučajevima, kad su ispunjeni određeni uvjeti. Ti su uvjeti za totalnu refleksiju sljedeći: upadni kut svjetlosti mora biti veći od kritičnog kuta, te indeks loma prvog sredstva mora biti veći od indeksa loma drugog sredstva. Pritom je kritični kut dan sljedećim izrazom:

gdje je n1 indeks loma prvog sredstva, a n2 indeks loma drugog sredstva. Za totalnu refrakciju postoji samo jedan uvjet, a taj je da jedno od sredstava propagacije svjetlosti između kojih svjetlost prolazi ima negativni indeks loma. U prirodni ne postoje tvari s takvim svojstvom, no, laboratorijski je moguće proizvesti određene materijale koji imaju negativni indeks loma.

Zanimljiv optički fenomen direktno vezan uz refrakciju (i refleksiju) jest kaustika. Kaustika je ovojnica zraka svjetlosti refraktiranih, ili reflektiranih, od zaobljene površine. Također, pod kaustikom se može podrazumijevati i projekcija te ovojnice na neku drugu površinu. Dobar primjer kaustike može proizvesti prazna staklena čaša na praznom stolu, na koju upada sunčeva svjetlost. Radi opetovanih refrakcija i refleksija zraka svjetlosti uvjetovanih strukturom čaše, izlazne zrake svjetlosti mogu na stolu projicirati neobičan oblik. Takvi se oblici općenito nazivaju kaustika (Slika 5).

Osim refleksije i refrakcije, dvaju najosnovnijih pojava koje dobro opisuju i geometrijska i fizikalna optika, svjetlost pokazuje i svojstva difrakcije i interferencije, koja se ne mogu objasniti geometrijskom optikom. Naime, difrakcija je pojava savijanja vala zbog neke prepreke. Premda je difrakcija uvijek prisutna, njeni su učinci primjetljivi tek ako je red veličine dimenzija prepreke jednak redu veličine valne duljine vala. Najpoznatiji primjer učinaka difrakcije bi bila stražnja strana CD-a, koja promatrana ispod izvora bijele svjetlosti stvara efekt duginih boja. Značajna primjena difrakcije su i hologrami, koji se primjerice koriste za zaštitu e-indeksa. Učinci difrakcije su uzrokovani interferencijom valova svjetlosti. Interferencija je superpozicija (zbrajanje) dvaju valova koji su međusobno koherentni (imaju istu frekvenciju). Ukoliko dva vala iste valne duljine, odaslana iz istog izvora, poradi neke prepreke budu savinuti (difrakcija), te se tako desi da propagiraju kroz isti prostor, s istim amplitudama i frekvencijama (jer imaju i iste valne duljine), ali međusobno pomaknuti u fazi, bit će ispunjeni uvjeti za interferenciju, pa će se interferencija i dogoditi. Očito, ovisno o pomaku u fazi, na nekim mjestima će i prvi i drugi val oba imati pozitivnu ili negativnu amplitudu, dok će na drugim mjestima jedan imati pozitivnu, a drugi negativnu amplitudu. To znači da će na nekim mjestima rezultirajući val imati povećanu amplitudu, a na nekim mjestima umanjenu amplitudu. Na primjeru CD-a, upadni valovi svjetlosti dopiru do premaza na stražnjoj strani CD-a, te zbog njegove mikroskopske strukture bivaju savinuti, dakle dolazi do difrakcije, što rezultira interferencijom. Upravo te valove koji nastaju kao rezultat interferencije percipiramo kao dugine boje. Dakako, defrakcijom i interferencijom se mogu objasniti i zakoni refleksije i refrakcije, koji vrijede ako je prepreka mnogo većih dimenzija od valne duljine vala.

Još jedna pojava vezana uz propagaciju svjetlosti, a koja se može objasniti isključivo valnom prirodom svjetlosti, jest polarizacija. Naime, općenito govoreći, valovi se mogu podijeliti na progresivne (putujuće) i stacionarne, a među progresivnima razlikujemo transverzalne i longitudinalne. Svjetlost jest progresivni, transverzalni val, što znači da se njegovo električno i magnetsko polje mijenjaju periodički u smjerovima okomitim na smjer gibanja vala. Kod nepolarizirane svjetlosti, vektori električnog i magnetskog polja zauzimaju s jednakom vjerojatnošću bilo koji smjer okomit na vektor širenja vala. To znači da se prirodna, nepolarizirana svjetlost sastoji od valova koji titraju u svim ravninama. S druge strane, polarizirana svjetlost je takva čiji valovi titraju u samo jednoj ravnini. Do polarizacije svjetlosti dolazi refleksijama i refrakcijama. Primjerice, odbljesak Sunca na površini mora jest polarizirana svjetlost. Iz tog razloga, kvalitetnije sunčane naočale su zapravo polarizacijski filtri, čime se ublažuju neugodni odbljesci. Inače, golim ljudskim okom je gotovo nemoguće razlikovati polariziranu od nepolarizirane svjetlosti – potrebne su posebne vježbe da bi osoba naučila zapažati veoma suptilni efekt pri promatranju polarizirane svjetlosti, nazvan Haidingerova četka.

Potrebno je spomenuti da u većini situacija, samo će dio upadne svjetlosti biti refleksiran i refraktiran, dok će ostatak biti absorbiran. Objašnjenje ove pojave daje čestična teorija svjetlosti – fotoni prilikom sudaranja s atomima mogu predati svoju energiju elektronu i time nestati, ili samo promijeniti smjer i brzinu. Naime, možemo zamisliti da se elektroni nalaze raspoređeni oko jezgre atoma ne na proizvoljnim udaljenostima, već u diskretnim razinama. Da bi elektron prešao iz niže u višu razinu, potrebno je da foton koji se sudari s njim ima točno odgovarajuću količinu energije, koja odgovara razlici više i niže energetske razine elektrona. Prijelazom elektrona iz niže u višu energetsku razinu, povećava se ukupna unutarnja energija tijela, odnosno, povećava se njegova toplina. U obrnutom slučaju, ukoliko elektron prelazi iz više u nižu razinu, višak energije se oslobađa u obliku fotona, čija je energija točno jednaka razlici energija više i niže razine. U ovim činjenicama leži razlog zašto različiti predmeti imaju različitu boju. Naime, bijela svjetlost sadrži sve vidljive valne duljine, što znači fotone svih frekvencija. Budući da je frekvencija fotona proporcionalna njegovoj energiji, a atom može absorbirati foton samo točno odgovarajuće energije (što ovisi o vrsti atoma), očito je da će samo dio fotona iz bijele svijetlosti biti absorbiran, a ostatak će biti odbijen, dakle, promijenit će im se smjer i brzina. Koje valne duljine svjetlosti će biti absorbirane, a koje reflektirane i refraktirane, ovisi o vrsti materijala, odnosno, o vrsti atoma od kojih je materijal sačinjen.

Sada možemo objasniti i pojavu ispodpovršinskog raspršivanja svjetlosti. Naime, kako fotoni upadaju na tijelo, neki bivaju absorbirani, dok se drugi odbijaju od atoma. Moguće je da neki od tih fotona nastave putovati unutar samog tijela, dakle ispod njegove površine. Drugim riječima, svjetlost kroz neka tijela može barem djelomično prolaziti, te se takva tijela nazivaju (djelomično) prozirna. U stvarnosti, sva su tijela prozirna bar u nekoj malenoj mjeri. Očitovanje  djelomične prozirnosti jest upravo u tome što se dio upadnih fotona raspršuje ispod površine tijela, te nakon opetovanih sudara napušta tijelo. Ova je pojava sveprisutna, iako je u većini slučajeva slabo zamjetna. Ispodpovršinsko raspršivanje se najčešće asocira s organskim materijalima, poput kože ili voska, ali i tvarima poput gume, mramora i slično. Na slici 6 možemo vidjeti dobar primjer homogenog raspršivanja svjetlosti kroz volumene dviju kocaka, unutar kojih naziremo obrise sadržanih neprozirnih tijela (u jednoj kugla, u drugoj stožac). Te unutarnje obrise raspoznajemo upravo radi efekta ispodpovršinskog raspršivanja svjetlosti.

Ovime smo ukratko pokrili sve bitne učinke i svojstva svjetlosti, promatrane kroz realne fizikalne modele. Budući da je naša primarna zadaća izraditi teorijski model osvjetljenja za koji je ključno da bude pogodan generiranju računalne grafike, već u ovome stadiju možemo uvesti određene aproksimacije. Naime, možemo primijetiti da većina pojava koje se mogu simulirati isključivo izračunom valnih svojstava svjetlosti, su ili ionako gotovo nemoguće za primijetiti (polarizacija svjetlosti), ili su izražajne tek u nekim posebnim slučajevima (primjerice, difrakcija svjetlosti na poleđini CD-a). Iz tog razloga, mnogo je isplativiji pristup simulacije isključivo geometrijske optike (što je računalno mnogo manje zahtjevno), te rješavanja posebnih slučajeva u kojima geometrijska optika nije dostatna raznim trikovima, kao što su pažljivo teksturiranje i slično.

Sad kad smo odredili glavne smjernice našeg modela osvjetljenja, možemo pokušati sažeti načela geometrijske optike u jedinstven matematički zapis. Prema dosad rečenome, možemo ponešto zaključiti o tome koliko bi bilo ukupno osvjetljenje u danoj točki prostora. Naime, znamo da je ukupna izlazna svjetlost u bilo kojoj točki prostora jednaka zbroju emitirane svjetlosti (što može biti nula, ukoliko nije riječ o izvoru svjetla), te doprinosima svih svjetlosnih zraka koje upadaju na tu točku, a mogu biti rezultat direktnog osvjetljenja drugim izvorom svjetlosti, ili pak rezultat (višestruke) refleksije svjetlosti od objekata na sceni. Također, znamo da se svjetlost reflektira od različitih objekata na drugačiji način, pa možemo definirati funkciju distribucije refleksivnosti (eng. bidirectional reflectance distribution function, BRDF), koja govori u kojoj mjeri se svjetlost reflektira od danog materijala. Sve dosad rečeno možemo formalno zapisati na sljedeći način:

gdje je:

Iako ovu jednadžbu nije teško postaviti, mnogo je veći problem točno je riješiti. Naime, ne samo da je problematično iznaći analitičko rješenje i prevesti ga u jednostavne operacije zbrajanja i množenja, koje računala mogu efikasno izvršavati, već vidimo i da potencijalna kompleksnost izračuna rješenja strmoglavo raste s kompleksnosti i međuodnosima objekata na sceni. Dakle, vidimo da smo suočeni s dva problema – prvi problem jest pronaći način za efikasno numeričko rješavanje dane integralne jednadžbe osvjetljenja. Drugi problem proizlazi iz zahtjeva za interaktivnošću – izvršavanje ovih izračuna mora biti u realnom vremenu. S vremenom se razvilo nekoliko pristupa i algoritama u računalnoj grafici, koji ili favoriziraju kvalitetu prikaza nauštrb interaktivnosti, ili pružaju interaktivnost nauštrb kvalitete. U prvoj skupini se nalaze algoritmi i metode koje pokušavaju raznim numeričkim metodama direktno riješiti jednadžbu iscrtavanja, te se zajednički nazivaju metode globalnog osvjetljenja. Primjerice, tu spadaju direktna simulacija geometrijske optike (ray traycing i srodni algoritmi), razne Monte Carlo metode (path tracing, photon mapping), te metode konačnih elemenata (radiosity). U drugu skupinu spadaju takozvani lokalni modeli osvjetljenja, koji su nastali kao aproksimacija jednadžbe iscrtavanja. Najosnovniji takav model jest Lambertov model refleksije, no mnogo popularnija je njegova proširena verzija poznata kao Phongov model. U sljedećim poglavljima će detaljnije biti objašnjene obje skupine algoritama, te prikazani pokušaji premošćivanja jaza između interaktivnosti i globalnog osvjetljenja.