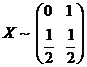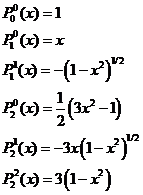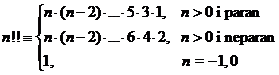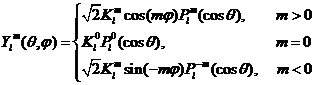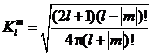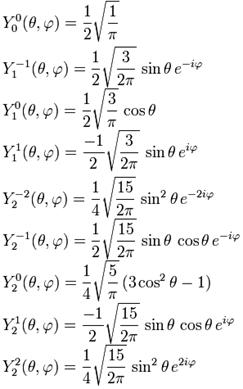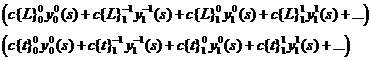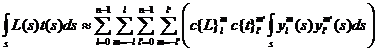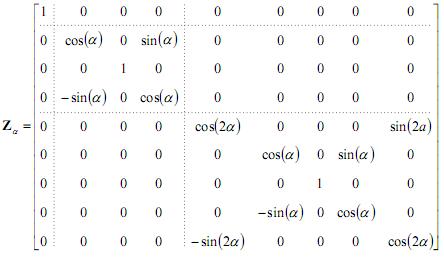Završni rad br. 38

U prošlom poglavlju predstavljen je efikasan algoritam temeljen na postupku isijavanja, gdje je efikasnost postignuta korištenjem aproksimacijskih, umjesto fizikalno točnih jednadžbi, uvođenjem kompromisa između broja koraka algoritma i kvalitete rezultata, te razvojem posebnih, dobro osmišljenih struktura podataka. Ipak, premda je algoritam dovoljno brz za upotrebu u interaktivnoj grafici na modernim računalima, čak i sa svim navedenim optimizacijskim mjerama, količina izračunavanja koju je potrebno izvršiti za svaku pojedinu generiranu sliku jest poprilična. Ukoliko je generiranje slika jedini zadatak, onda je takvo stanje stvari i prihvatljivo, no, većina interaktivnih aplikacija čija je svrha predočavanje virtualnih okruženja, obično sadrže i razne druge komponente, nevezane direktno uz samu grafiku. Odličan primjer takvih aplikacija su igre, koje predstavljaju jednu od vodećih sila razvoja računalne grafike, a osim same grafike uključuju i raznovrsne druge discipline i tehnologije poput umjetne inteligencije, fizikalnih simulacija, baza podataka, kompleksnih server-klijent arhitektura itd. Također, i raznovrsne specijalizirane poslovne aplikacije osim samog grafičkog prikaza, obično uključuju i dodatnu, specifičnu funkcionalnost vezanu uz njihovu primjenu. Sva ta dodatna funkcionalnost i sama značajno opterećuje računalni sustav, što znači da treba uzeti u obzir da će u praktičnim primjenama za sam postupak iscrtavanja biti dostupan tek dio ukupnih računalnih resursa. Ideja koja se prirodno nameće jest da pokušamo smanjiti količinu posla koji je potrebno obaviti prilikom samog iscrtavanja, tako da što je više moguće posla obavimo prije iscrtavanja, u predfazi, koja se može obaviti odvojeno od glavnog programa. Takva ideja nije nova, te se koristi u interaktivnoj računalnoj grafici već barem desetljeće, u obliku takozvanih mapa svjetlosti (eng. lightmap). Princip je vrlo jednostavan – budući su algoritmi poput isijavanja prespori za upotrebu u interaktivnim aplikacijama, takav se algoritam jednostavno izvrši prije pokretanja same aplikacije, te se rezultat pohrani u obliku običnih tekstura, nazvanih mape svjetlosti. Pojedina mapa svjetlosti se sastoji od isključivo sivih tonova, gdje tami dijelovi odgovaraju sjenama, a svijetli osvjetljenim područjima. Očito, ovakvim se pristupom mogu dobro simulirati meke sjene i fini prijelazi u ambijentalnom osvjetljenju, za čiji izračun može poslužiti bilo koji od globalnih algoritama osvjetljenja. Sve što glavna aplikacija tada mora učiniti, jest učitati te dodatne teksture i priložiti ih sceni, na isti način kao i sve obične teksture. Gubitak performansi je u tom slučaju gotovo nezamjetan, no prisutna su bitna ograničenja. Naime, budući da zasjenjenost pojedinih područja scene ovisi o geometrijskom odnosu objekata koji sačinjavaju danu scenu, ti geometrijski odnosi moraju biti poznati prije pokretanja glavne aplikacije. Isto tako, ukoliko bi došlo do geometrijskih promjena scene (deformacija ili pomicanje objekata uslijed animacije), predizračunate mape svjetlosti više ne bi vrijedile, pa bi došlo do vidljivih i očitih artefakata. Osim toga, mape svjetlosti ovise i o položaju i karakteristikama izvora svjetlosti koji obasjavaju scenu, tako da nije moguće imati niti dinamička svjetla.  Algoritam predizračunatog prijenosa zračenja, koji će biti opisan u ovom poglavlju, jest konceptualno istovjetan mapama svjetlosti, no koristi matematički mnogo naprednije metode, te stoga pruža još kvalitetnije rezultate. Iz tog razloga, bit će ostvariva i dinamička svjetla, no nažalost, algoritam će i dalje biti ograničen na isključivo geometrijski statičke scene.

Međutim, prije opisa samog algoritma, prisjetimo se na trenutak jednadžbe iscrtavanja. Kako je već rečeno, upravo integralni član te jednadžbe predstavlja suštinski problem kojeg računalna grafika pokušava riješiti. No, može se postaviti naizgled naivno pitanje – budući da su već razvijeni veoma moćni matematički paketi za simboličke izračune kao što su Wolfram Mathematica ili MATLAB, koji su sposobni riješiti gotovo svaku zamislivu integralnu jednadžbu, zašto se uopće razvijaju razni algoritmi iscrtavanja? Zašto ne bismo jednostavno upotrijebili neki od postojećih modela simboličkog izračunavanja za analitičko rješavanje jednadžbe iscrtavanja? Upravo u „simboličkom računanju“ leži problem! Naime, da bi se neka jednadžba mogla simbolički riješiti, mora biti poznat njen oblik i simbolički zapis. U našem slučaju, to nije moguće. Podintegralna jednadžba je u našem slučaju definirana karakteristikama scene koju želimo iscrtati, a budući da scene mogu biti veoma raznolike, s vrlo kompleksnim međuodnosima objekata, eksplicitan zapis funkcije osvjetljenja će općenito biti prekompleksan za bilo kakvu praktičnu primjenu. Iz tog razloga, općeniti postupak pronalaženja eksplicitnog, simboličkog oblika funkcije osvjetljenja ne postoji. Ipak, taj se postupak može osmisliti i provesti za neke posebne slučajeve, primjerice ako pretpostavimo da je ambijentalno osvjetljenje savršeno homogeno u svakoj točki prostora. U tom posebnom slučaju je problem pronalaženja simboličkog zapisa funkcije osvjetljenja trivijalan, budući da je riječ o tek jednoj konstanti. Upravo je ova pretpostavka temeljna ideja svih lokalnih modela svjetlosti, dok globalni algoritmi predstavljaju raznovrsne pristupe numeričkoj aproksimaciji pravog, analitičkog rješenja jednadžbe iscrtavanja. Svi su ti pristupi razvijeni dobrim poznavanjem domene računalne grafike, i njoj srodnih fizikalnih domena. Međutim, danas su u matematici poznate različite općenite metode numeričkog rješavanja integralnih i diferencijalnih jednadžbi, koje ne ovise o domeni ili kontekstu primjene. Dakako, neku (odgovarajuću) od tih općenitih metoda možemo pokušati upotrijebiti i za rješavanje jednadžbe iscrtavanja. Algoritam predizračunatog prijenosa zračenja se jednim dijelom temelji na upravo takvoj metodi, koja se naziva Montle Carlo integracija. Osnovna ideja te metode jest promatranje podintegralne funkcije kao crne kutije, dakle objekta nepoznatog oblika i interne strukture. Potrebno je poznavati tek skup točaka koje nastaju funkcijskim preslikavanjem iz odabrane domene, gdje je još poželjno da ta domena ima određena korisna svojstva. Sam postupak se izvodi iz teorije vjerojatnosti, stoga je potrebno definirati i objasniti određene temeljne pojmove koje ćemo koristiti. Osnovni koncept u teoriji vjerojatnosti jest slučajna varijabla. Ukoliko zamislimo pokus u kojem bacamo novčić, možemo reći da postoje dva osnovna, međusobno isključiva ishoda – palo je pismo, i pala je glava. Ti ishodi se nazivaju elementarni događaji, a svi postojeći elementarni događaji tvore prostor događaja. Slučajnu varijablu tada možemo definirati kao funkciju čija je domena prostor događaja, a koja preslikava elementarne događaje u realne brojeve. Na primjeru bacanja novčića, možemo definirati slučajnu varijablu X na sljedeći način:

Zatim možemo definirati i zakon razdiobe te slučajne varijable, koji govori kolika je vjerojatnost da varijabla poprimi neku specifičnu vrijednost. U gornjem primjeru, zakon razdiobe bi izgledao ovako:

U gornjem retku se nalaze sve moguće vrijednosti koje varijabla može poprimiti, a u donjem retku su redom zapisane odgovarajuće vjerojatnosti tih vrijednosti. Ovako definirana slučajna varijabla se naziva diskretnom varijablom, budući da postoji konačan skup vrijednosti koje može poprimiti, koje odgovaraju konačnom broju događaja. Međutim, nama će biti zanimljivije kontinuirane varijable, koje se definiraju nad beskonačnim prostorom događaja, i koje mogu poprimiti beskonačan broj vrijednosti. Kontinuirana slučajna varijabla se primjerice može definirati za pokus u kojem nasumično biramo broj iz intervala [0, 1]. Budući da za realne brojeve vrijedi da u svakom intervalu postoji beskonačan broj različitih brojeva, tako i slučajna varijabla može poprimiti beskonačan broj različitih vrijednosti. Slično kao što se za diskretne varijable definira zakon razdiobe, tako se za kontinuirane varijable definira funkcija razdiobe:

Naime, budući da je domena beskonačna, općenito će nas zanimati samo vjerojatnost da je varijabla poprimila vrijednost manju od neke zadane, a ne točan iznos. Još jedan izrazito važan pojam vezan uz kontinuirane slučajne varijable jest funkcija gustoće, koja se definira kao derivacija funkcije razdiobe. Drugim riječima, vrijedi sljedeće:

gdje je g(t) funkcija gustoće. Važno svojstvo funkcije gustoće jest da njen integral po cijelom skupu realnih brojeva mora biti jednak jedan. Također, vrijedi da za svaku slučajnu varijablu postoji neka vrijednost koju ta varijabla najčešće poprima, a ta se vrijednost naziva očekivanje varijable. Očekivanje možemo definirati na sljedeći način:

Budući da su i same slučajne varijable ništa drugo doli funkcije s određenim svojstvima, možemo proširiti gornju definiciju očekivanja na općenite funkcije:

No, očekivanje neke funkcije se može (približno) izračunati i na drugi način, na temelju Zakona velikih brojeva. Taj zakon kaže da ukoliko su poznate vrijednosti funkcije za velik broj različitih točaka, tada je očekivanje te funkcije približno jednako aritmetičkoj sredini svih poznatih uzoraka. Matematički, taj rezultat možemo zapisati ovako:

Bitna napomena jest da ovaj zakon vrijedi samo ukoliko su uzorci nasumično, uniformno distribuirani. Dakako, što je veći broj uzoraka, to će rezultat biti točniji. Prethodne dvije relacije sada možemo izjednačiti, te time dobivamo sljedeći rezultat:

Kao što vidimo, integral neke proizvoljne funkcije f(x) možemo aproksimirati aritmetičkom sredinom slučajnih uzoraka te funkcije, skaliranih nekim težinskim faktorom (koji odgovara vrijednosti funkcije gustoće). Upravo opisani postupak se naziva Monte Carlo integracija. Sad je očito kako se može integrirati funkcija čiji eksplicitan oblik nije poznat – korištenjem ove numeričke metode, dovoljno je poznavati tek određen skup točaka funkcije čiji integral tražimo. Da bismo mogli upotrijebiti ovu metodu za rješavanje jednadžbe iscrtavanja, potrebno je još samo odgovoriti na dva pitanja. 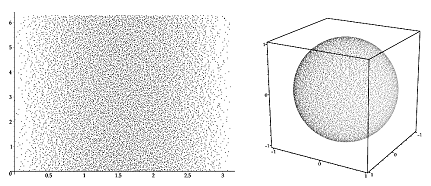Naime, budući da je jednadžba koju rješavamo definirana kao integral preko površine kugle, postavlja se pitanje kako uniformno raspodijeliti uzorke preko sfere. Također, moramo pronaći i težinske faktore, odnosno odgovarajuću funkciju gustoće. Prvi problem ćemo lako riješiti korištenjem takozvane kanonske uniformne varijable, koja poprima vrijedosti u intervalu [0, 1), i to tako da svaka vrijednost ima jednaku vjerojatnost pojavljivanja. Ukoliko uzmemo da kanonske varijable X i Y označavaju pravokutne koordinate točaka, možemo ih projicirati na površinu sfere pomoću sljedeće transformacije:

Budući da uzorke biramo uniformno, funkcija razdiobe je takva da je njen iznos proporcionalan duljini intervala u kojem se uzorak nalazi. Naime, pošto je funkcija razdiobe definirana kao P(X < x), što je x veći, to je širi interval u kojem se X može nalaziti, a to znači i da je veća vjerojatnost da će se X nalaziti u tom intervalu. Drugim riječima, u našem slučaju funkcija razdiobe jest linearna, a ukoliko se prisjetimo da je funkcija gustoće definirana kao derivacija funkcije razdiobe, lako zaključujemo da funkcija gustoće mora biti tek jedna konstanta. Iz uvjeta da integral funkcije gustoće mora biti jedan, lako dobivamo da je njen iznos jednak recipročnoj vrijednosti oplošja kugle, a pošto radimo s jediničnom kuglom, ta je vrijednost jednaka 1/4π. Sad napokon možemo napisati konačan izraz za numeričku aproksimaciju integrala, koji možemo direktno upotrijebiti za rješavanje jednadžbe iscrtavanja:

Doista, naprednim matematičkim aparatom uspjeli smo prevesti jednadžbu iscrtavanja iz oblika koji je nerješiv direktno na računalu, u oblik koji to jest, korištenjem isključivo jednostavnih operacija množenja i zbrajanja. Budući da direktno rješavamo jednadžbu iscrtavanja, sasvim sigurno ćemo obuhvatiti apsolutno sve optičke efekte koje svjetlost proizvodi svojom propagacijom (dakako, ne uzimajući u obzir pojave zbog valne prirode svjetlosti, koje jednadžba iscrtavanja ne opisuje). Međutim, ako malo bolje pogledamo gornji izraz, i sjetimo se da ćemo ga morati izračunavati za svaki vrh svih poligona koji sačinjavaju scenu, vidimo da je tu uključeno doista mnogo računanja. Ukoliko pretpostavimo da se na sceni nalazi stotinu tisuća vrhova (što je uobičajeno za današnje standarde), te da koristimo deset tisuća slučajnih uzoraka, dolazimo do brojke od jedne milijarde operacija množenja i zbrajanja po slici, za cjelokupnu scenu. Dakako, sama ta evaluacija integrala se može provesti tek nakon što su poznati uzorci funkcije osvjetljenja, a da bi oni bili izračunati, potrebno je odrediti karakteristike scene, dakle geometrijske međuodnose objekata na sceni. Algoritam koji efikasno rješava taj problem jest praćenje zrake, koji je i sam po sebi još uvijek vrlo zahtjevan za većinu osobnih računala. Doduše, to određivanje međuodnosa objekata na sceni se može provesti kao predprocesiranje scene, ukoliko koristimo statičku geometriju, takvu da se objekti ne pomiču niti deformiraju za cjelokupno trajanje simulacije. Dakle, u predfazi algoritma iscrtavanja, a po potrebi čak i nekom aplikacijom odvojenom od glavnog programa, može se provesti algoritam praćenja zrake i na temelju toga generirati potrebni uzorci. No, još uvijek ostaje problem evaluacije same jednadžbe iscrtavanja, što je postupak koji se za detaljne scene može sastojati, kako smo prethodno utvrdili, i od milijarde operacija! Očito, opisani postupak je praktički neupotrebljiv, no razlog tomu je što je algoritam u predstavljenom obliku još uvijek nepotpun. U ovom trenutku možemo uvesti još jednu matematičku tehniku koja se često koristi za rješavanje raznih fizikalnih i drugih problema, a koja će na vrlo elegantan način drastično reducirati broj potrebnih operacija za vrijeme samog iscrtavanja. Riječ je o rastavljanju proizvoljnih funkcija u takozvane bazne funkcije, za što se obično odabiru neki jednostavni polinomi ili trigonometrijske funkcije. Ideja je zatim sljedeća: odgovarajućim skaliranjem i zbrajanjem nekog broja tih baznih funkcija se dobiva bolja ili lošija aproksimacija početne funkcije. Ukoliko označimo početnu funkciju sa f(x), i-tu baznu funkciju sa B_i(x), a koeficijent za skaliranje i-te bazne funkcije sa c_i, onda prethodnu rečenicu možemo matematički zapisati ovako:

Jedini problem koji moramo riješiti jednom kad smo odabrali bazne funkcije, jest odrediti odgovarajuće koeficijente za danu početnu funkciju, koji govore koliko je ta funkcija „slična“ pojedinim baznim funkcijama. Postupak njihovog izračunavanja se svodi na integriranje umnoška početne funkcije i neke bazne funkcije, po cijeloj domeni početne funkcije, dakle:

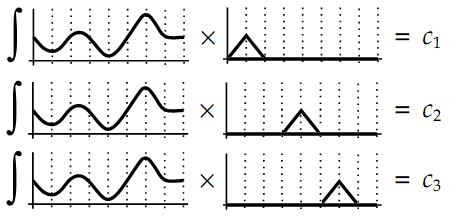
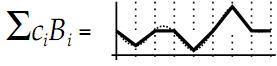
Možda je najjednostavnije predočiti si ovaj postupak grafički. Zamislimo da imamo neku krivuljnu početnu funkciju, i tri linearne bazne funkcije. Postupak određivanja koeficijenata bi tada izgledao ovako:

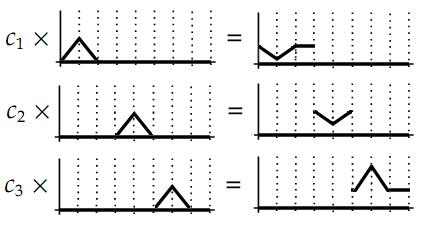
Jednom kad imamo izračunate koeficijente, možemo ih pomnožiti s baznim funkcijama, i time skalirati bazne funkcije na potrebnu amplitudu:

Nakon toga, skalirane bazne funkcije trebamo samo zbrojiti, i dobit ćemo aproksimaciju početne funkcije:

Sam postupak rastavljanja proizvoljne funkcije u sumu baznih funkcija se naziva projekcija, a pojedini članovi te sume se ponekad nazivaju harmonicima. Odabir vrste projekcije (odnosno, oblika baznih funkcija) ovisi o kontekstu primjene i svojstvima funkcije koju želimo aproksimirati. U našem slučaju, budući da je funkcija osvjetljenja definirana preko sfere, odgovarat će nam projekcija u takozvane sferne harmonike. Ova vrsta projekcije se zasniva na određenom obliku polinoma, koji se nazivaju asocirani Legendre polinomi. Ti polinomi se definiraju pomoću dvaju parametara, l i m, te je njihova uobičajena oznaka . Parametar l se naziva pojasom polinoma, i može biti bilo koji cijeli broj ili nula, dok m mora biti u intervalu [0, l]. Dakle, polinomi su podijeljeni u pojaseve, takve da svaki sljedeći pojas sadrži točno jedan polinom više od prethodnog. Domena asociranih Legendre polinoma su realni brojevi na intervalu [-1, 1]. Prvih nekoliko takvih polinoma izgleda ovako:

Asocirani Legendre polinomi se definiraju kao rješenja istoimene diferencijalne jednadžbe, no postoje drugi načini kako se oni mogu generirati. Najjednostavniji način, koji je ujedno i najprimjereniji za implementaciju na računalu, jest korištenje rekurzivnih relacija. Osnovna takva relacija jest sljedeća:

         (1)

Primjetimo da je parametar m konstantan, te da se mijenja isključivo parametar l. To znači da ovom relacijom možemo iz poznavanja dvaju polinoma s istim rednim brojem, ali iz dvaju susjednih pojasa, izračunati treći polinom, koji će se nalaziti u trećem pojasu po redu (počevši od pojasa prvog polinoma), i imati isti redni broj unutar svog pojasa kao i početna dva polinoma. No, osim ove temeljne relacije, može se izvesti i pomoćna, nešto jednostavnija relacija:

                                         (2)

Ova relacija vrijedi samo u slučaju da poznajemo polinom čiji je redni broj unutar pojasa jednak rednom broju pojasa. Tada možemo jednostavno podignuti taj polinom u sljedeći pojas. Osim ovih rekurzivnih relacija, za asocirane Legendre polinome vrijedi i sljedeće zanimljivo svojstvo:

                       (3)

Riječima, ovo svojstvo znači da se polinom čiji je redni broj unutar pojasa jednak rednom broju samog pojasa može dobiti pomoću direktne formule, bez potrebe za postepenim, iterativnim računanjem jednog po jednog polinoma. U gornjoj formuli se javlja operator !!, što je oznaka dvostrukog faktorijela, a koji je definiran na sljedeći način:

Promatranjem gornjih triju relacija, lako možemo osmisliti efikasan način za generiranje asociranih Legendre polinoma proizvoljnih parametara l i m. Očito, najjednostavnije je evaluirati posljednju relaciju, koja pruža direktno rješenje. Doduše, ona se sastoji od dvostrukog faktorijela koji je i sam rekurzivna relacija, no vremenska kompleksnost računanja faktorijela se može svesti na konstantu upotrebom tablice predizračunatih vrijednosti. Dakle, ideja je sljedeća: za zadane parametre l i m, prvo se izračuna intermedijarni polinom korištenjem relacije (3). Rezultirajući polinom će biti oblika , te ukoliko je l = m, onda je to konačno rješenje. U suprotnom slučaju, budući da prema definiciji mora vrijediti m ≤ l, zaključujemo da je m sigurno manji od l. To znači da jednom kad je određen polinom s traženim parametrom m, ukoliko je l različit od m, potrebno je samo podizati pojas dobivenog intermedijarnog polinoma dok se ne dosegne l-ti pojas. Ovo se može postići relacijama (2) i (1). Ukoliko je l = m + 1, dovoljna je samo relacija (2), koja odmah daje konačno rješenje. Ukoliko to nije slučaj, onda je još potrebno iskoristiti i relaciju (1). Naime, pomoću relacije (3) smo dobili prvi intermedijarni polinom, a pomoću relacije (2) drugi. No, taj drugi dobiveni polinom očito više nije oblika , nego , pa nam je preostala samo relacija (1). Tom relacijom iz  i  dobivamo . Po potrebi, iz  i  možemo dobiti , i tako dalje, dok ne dosegnemo zadani pojas. Ovime smo pokrili svo znanje o asociranim Legendre polinomima koje je potrebno za korištenje sfernih harmonika, pa je vrijeme da ih matematički definiramo. Uobičajena oznaka jest , gdje parametri l i m imaju isto značenje kao i kod asociranih Legendre polinoma. Jasno, budući da je riječ o funkciji definiranoj preko površine kugle, njeni su parametri dani u obliku sfernih koordinata (θ,φ). Sferni harmonici se općenito definiraju kao kompleksne funkcije, no nas će zanimati samo realni dio:

gdje je  odgovarajući asocirani Legendre polinom, dok je  faktor za skaliranje koji se računa na sljedeći način:

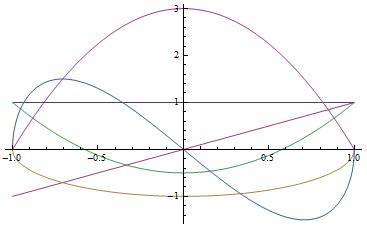
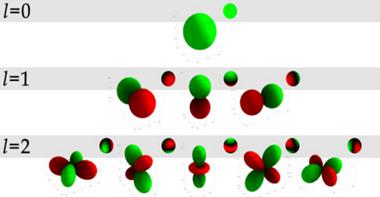
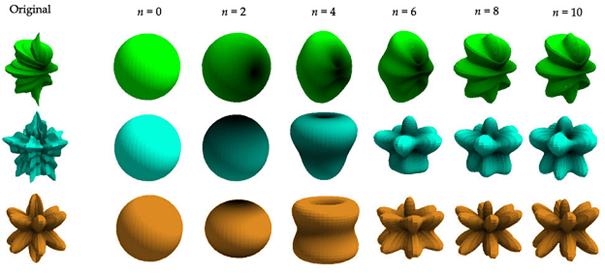
Valja primjetiti da je za uvođenje sfernih harmonika potrebno malo proširiti prethodnu definiciju asociranih Legendre polinoma. Naime, rekli smo da mora vrijediti l ≤ 0, 0 ≤ m ≤ l. Međutim, za funkcije sfernih harmonika, potrebno je proširiti dozvoljeni interval parametra m tako da uključuje i negativne vrijednosti, dakle da vrijedi –l ≤ m ≤ l. Za ilustraciju, funkcije sfernih harmonika prvih triju pojaseva izgledaju ovako u općem obliku:

Kako je već rečeno, općeniti postupak za projekciju neke početne funkcije u bazne funkcije jest izračun odgovarajućih koeficijenata, a koji se računaju kao integral umnoška početne funkcije i baznih funkcija. U našem konkretnom primjeru, može se izvesti sljedeća formula za dobivanje pojedinih koeficijenata:

Međutim, funkciju koju ćemo htjeti projicirati – funkciju osvjetljenja – nije moguće, kako smo već utvrdili, zapisati u eksplicitnom, simboličkom obliku, već je moguće samo procijeniti njenu vrijednost u nekom skupu točaka, korištenjem algoritma praćenja zrake ili nekog sličnog. No, vidimo da smo upravo taj problem već riješili, uvođenjem Monte Carlo integracije! Ukoliko se prisjetimo prethodno dobivenog rezultata za numeričku aproksimaciju integrala,

možemo povezati taj rezultat sa formulom za koeficijente projekcije, pa dobivamo sljedeće:

Prebacivanjem u pravokutne koordinate, dobivamo konačni oblik formule, koji je najprimjereniji za implementaciju na računalu:

gdje je  funkcija sfernog harmonika izražena u pravokutnim koordinatama. Rekonstrukcija početne funkcije se tada vrši jednostavnim sumiranjem umnožaka koeficijenata i sfernih harmonika. Ukoliko se dogovorimo da  predstavlja oznaku projekcije funkcije  u sferne harmonike, onda se projekcija n-tog reda definira ovako:

U ovom trenutku možemo opisati neka bitna svojstva sfernih harmonika, koja ih čine idealnim izborom baznih funkcija za projekciju funkcije osvjetljenja. Osnovno svojstvo, koje predstavlja i glavni razlog upotrebe upravo sfernih harmonika, jest ortonormalnost. Za neki skup funkcija se kaže da je ortonormalan ukoliko za svaki par funkcija tog skupa  vrijedi da je integral umnoška tih dviju funkcija jednak ili 0 ili 1. U slučaju da su funkcije istovjetne, rezultat je 1, a u suprotnom slučaju 0. Matematički, ovo možemo zapisati na sljedeći način:

Bitnost ovog svojstva možemo uočiti ukoliko se prisjetimo jednadžbe iscrtavanja:

Radi jasnoće, njen integralni član možemo sažeto zapisati u sljedećem obliku:

gdje je L(s) funkcija upadne svjetlosti, što odgovara izrazu , a t(s) funkcija prijenosa, koja predstavlja sažet prikaz distribucije reflektivnosti zračenja i atenuaciju svjetlosti, dakle, odgovara izrazu . Projekcijom funkcija L(s) i t(s) u sferne harmonike dobivamo sljedeće:

Ukoliko upotrijebimo definiciju projekcije, gornje podintegralne funkcije možemo ovako zapisati:

Oznake  i  označavaju redom koeficijente projekcija funkcija L(s) i t(s). Ukoliko sada ove izraze uvrstimo u jednadžbu iscrtavanja, dobivamo sljedeće:

Raspišimo sad ove dvije dvostruke sume za prvih nekoliko članova:

Nakon množenja tih izraza, dobivamo:

Dakle, imamo sumu umnožaka koeficijenata i sfernih harmonika obaju projekcija, što možemo sažeto zapisati:

Budući da su integracija i sumacija linearni operatori, možemo im promijeniti redosljed:

Prema svojstvu ortonormalnosti, slijedi da će integral na desnoj strani jednadžbe uvijek biti jednak jedinici za m = m', l = l', i jednak nuli za sve druge slučajeve, pa možemo izbaciti unutarnje dvije sumacije i dobiti ovaj mnogo jednostavniji izraz:

Ako bolje pogledamo što smo dobili, vidimo da smo uspjeli svesti integral preko površine sfere na jednostavno množenje i zbrajanje koeficijenata! Dakako, istu stvar smo postigli i direktnim numeričkim rješavanjem jednadžbe iscrtavanja, no postoji značajna razlika u efikasnosti. Kod direktnog rješavanja jednadžbe, za svaki vrh poligona koji sačinjavaju scenu potrebno je ponoviti jedno množenje i jedno zbrajanje onoliko puta koliko imamo uzoraka, što u praktičnim primjenama može biti i desetak tisuća. S druge strane, ukoliko provedemo projekciju u sferne harmonike, pokazat će se da je i 16 koeficijenata po vrhu sasvim dovoljno za kvalitetne rezultate, što znači da je dovoljno tek 16 operacija množenja i zbrajanja po vrhu. Drugim riječima, algoritam je sada doslovno postao tisuću puta brži!

Sferni harmonici posjeduju još jedno izrazito korisno svojstvo, a to je rotacijska invarijantnost. Naime, zamislimo da imamo dvije funkcije, f i g. Funkciju f projiciramo u sferne harmonike, a zatim izvršimo rotaciju za neki kut oko neke osi. S druge strane, funkciju g prvo rotiramo za isti taj kut oko iste te osi, a zatim projiciramo. Ukoliko su f i g istovjetne funkcije, onda će i rezultati oba postupka biti istovjetni. Drugim riječima, svejedno je da li prvo rotiramo funkciju pa ju projiciramo, ili prvo projiciramo pa rotiramo. Ovo odlično svojstvo će omogućiti dinamička svjetla, budući da ćemo funkciju upadnog svjetla, u gornjim jednadžbama označenu s L(s), moći rotirati i nakon projekcije. Sama rotacija koeficijenata se jednostavno postiže matričnim množenjem, a jedini je problem konstruirati odgovarajuću matricu. Naime, dimenzije rotacijske matrice očito ovise o broju koeficijenata s kojima računamo, a budući da broj potrebnih koeficijenata ovisi o redu sferne projekcije (za projekciju n-tog reda potrebno je n² koeficijenata), i dimenzije rotacijske matrice također ovise o redu projekcije. To znači da je potrebno pronaći način za generiranje rotacijskih matrica danog reda. Može se pokazati da će za n-ti red projekcije, rotacijska matrica biti dimenzija n²× n², te se može izgraditi pomoću rekurzivnog postupka. Pritom ćemo pretpostaviti da se rotacija vrši pomoću Eulerovih kuteva, dakle, kao niz od tri rotacije oko koordinatnih osi, pri čemu je potrebno odabrati redosljed komponenti rotacije. Najpovoljniji izbor redosljeda rotacija jest oko ZYZ osi. Naime, tada da su nam dovoljne samo dvije vrste rotacija, oko Z osi , i oko Y osi, pri čemu se rotacija oko Y osi može dodatno rastaviti na rotaciju oko X osi za 90 stupnjeva, zatim rotaciju oko Z osi, te rotaciju oko X osi za -90 stupnjeva. Dakle, izraz za konačnu matricu rotacije sfernih harmonika glasi:

Dakako, još moramo odrediti i same matrice X i Z. Jedan način kako se to može postići jest upotrebom istog principa koji omogućuje projekciju neke krivulje u bazne funkcije. Naime, prisjetimo se značenja koeficijenata baznih funkcija – oni preslikavaju bazne funkcije u segmente početne krivulje! Prema tome,  možemo istu tehniku koristiti za preslikavanje ne-rotiranih koeficijenata u rotirane. Pojedini koeficijenti ove projekcije se dobivaju na potpuno isti način koji vrijedi za sve projekcije, dakle integracijom umnoška početne i bazne funkcije, što u našem slučaju daje:

gdje su  rotirane funkcije sfernih harmonika, a  ne-rotirane. Gornji izraz je zapisan u takvom obliku, da se dobiveni koeficijenti  lako zapišu u matričnom obliku. Dakako, pravila matričnog množenja će osigurati da množenjem ove matrice s ne-rotiranim koeficijentima projekcije u sferne harmonike dobijemo upravo rotirane koeficijente. Primjenom opisane tehnike, možemo izračunati matricu rotacije oko Z osi za neki kut α, za prva tri pojasa:

Odmah uočavamo vrlo zanimljivu pojavu – elementi matrice koji odgovaraju pojedinim pojasevima su odvojeni, i ne utječu jedan na drugoga. Također, nulti pojas se sastoji samo od jedne jedinice, dok se prvi pojas sastoji od jedinice oko koje su raspoređeni sinusi i kosinusi. Nadalje, drugi pojas se sastoji od elemenata nultog pojasa (jedinice u sredini), elemenata prvog pojasa (sinusa i kosinusa raspoređenih oko jedinice u sredini), te sinusa i kosinusa dvostrukog kuta, koji su opet raspoređeni istim redosljedom oko elemenata prethodnih pojaseva. Doista, matematičkom indukcijom se može dokazati da se svaki sljedeći pojas sastoji od svih elemenata prethodnih pojaseva, te dodatnih sinusa i kosinusa kuta Nα. Također, i matrica rotacije oko X osi se može izgraditi na analogan način. Ovime smo pronašli jednostavan i efikasan rekurzivan postupak za generiranje rotacijskih matrica, koji se lako može implementirati na računalu.

Na kraju, nakon upoznavanja potrebne matematičke pozadine, možemo rezimirati glavne korake algoritma predizračunatog prijenosa zračenja. Predfaza se sastoji od sljedećih koraka:

1. Generiranje dovoljne količine uniformnih uzoraka površine sfere.
2. Za svaki uzorak, izračuna se vrijednost funkcije sfernih harmonika, za prvih n pojaseva.
3. Za svaki vrh poligona koji sačinjavaju scenu, procijeni se funkcija prijenosa svjetlosti, pomoću algoritma praćenja zrake. Ta funkcija mora uključivati barem distribuciju reflektivnosti, a može uključivati i detekciju sjena (tehnika zrake sjene, opisana u poglavlju o praćenju zrake), rekurzivnu sumaciju indirektnih doprinosa osvjetljenja, te ispodpovršinsko raspršivanje.
4. Paralelno s računanjem funkcije prijenosa, vrši se Monte Carlo integracija umnoška funkcije prijenosa i prethodno izračunatih vrijednosti funkcija sfernih harmonika. Ovime se dobivaju koeficijenti projekcije funkcije prijenosa za svaki pojedini vrh.
5. Koeficijenti izračunati za svaki vrh se zapisuju u datoteku, za kasniju upotrebu pri iscrtavanju scene.

Jednom kad je predprocesiranje scene dovršeno, može započeti samo iscrtavanje, koje se sastoji od sljedećih koraka:

1. Projekcija funkcije osvjetljenja u sferne harmonike. Ta funkcija može biti vrlo jednostavna, npr. konstanta, ili pak neka od funkcija koje opisuju jačinu Sunčevog zračenja (ovisno o potrebama aplikacije). Ovaj korak je dovoljno izvršiti tek jedamput, za svako svjetlo na sceni.
2. Prilikom svakog iscrtavanja slike, za svaki vrh poligona koji sačinjavaju scenu izračuna se skalarni umnožak vektora koeficijenata (učitanih iz datoteke) sa zbrojenim vektorom koeficijenata svih svjetala na sceni (po potrebi, taj se vektor još rotira, množenjem s rotacijskom matricom). Dobiveni broj predstavlja svjetlinu danog vrha, i može se shvatiti kao (monokromatska) boja vrha. Ovaj korak sjenčanja vrha se može vrlo efikasno implementirati jezikom sjenčanja, tako da se izvršava na grafičkoj kartici, paralelno s transformacijom vrha.