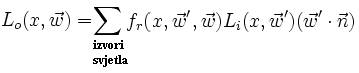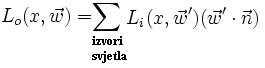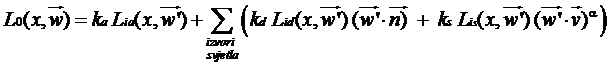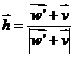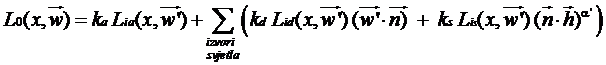Osnovna ideja svih lokalnih modela osvjetljenja, po kojoj su i dobili naziv, jest zanemarivanje globalnih učinaka propagacije svjetlosti. Naime, kako je rečeno u prethodnom poglavlju, ukupno osvjetljenje u danoj točki prostora je jednako zbroju doprinosa svih zraka svjetlosti koje upadaju, ili bivaju emitirane s te točke. Odnosno, možemo reći da kako svjetlost iz nekog izvora upada na objekte na sceni, te biva reflektirana, tako ti objekti djeluju kao sekundarni izvori osvjetljenja, i stvaraju ambijentalno osvjetljenje uz razne popratne učinke poput pretapanja boja. Upravo ovoj pojavi odgovara integralni član jednadžbe iscrtavanja:  

Budući da upravo ovaj član jednadžbe predstavlja glavninu poteškoća pri računanju osvjetljenja, prirodno se nameće ideja za njegovom aproksimacijom, ili čak potpunim zanemarivanjem. Naime, analiziranjem velikog broja raznolikih prirodnih uvjeta osvjetljenja, lako se može uočiti da je u većini slučajeva indirektno osvjetljenje, nastalo refleksijom svjetlosti između objekata na sceni, za red veličine manjeg intenziteta od direktnog osvjetljenja. Također, direktno osvjetljenje pokazuje oštre prijelaze u intenzitetu, te stoga iscrtava i oštre sjene. S druge strane, oscilacije u indirektnom osvjetljenju kroz prostor su veoma blage, to jest, indirektno osvjetljenje je približno ravnomjerno rasprostranjeno u prostoru, sa tek blagim gradijentima u intenzitetu, te stoga stvara i blage, meke sjene. Ukoliko bi indirektno, ambijentalno osvjetljenje doista bilo potpuno homogeno, tada bi izraz za intenzitet indirektnog osvjetljenja u bilo kojoj točki prostora bio sveden na jednu jedinu konstantu. Drugim riječima, jednadžba iscrtavanja tada prestaje biti integralna jednadžba, i biva svedena na proračun isključivo direktnog osvjetljenja – što znači jednostavno zbrajanje i množenje:

Upravo je ova ideja temelj svih lokalnih modela osvjetljenja, i time interaktivne računalne grafike. No, premda je ovakav oblik jednadžbe iscrtavanja daleko jednostavniji za izračunavanje od početnoga, postoji još jedan trik koji se sve do nedavno redovito i bez iznimke primjenjivao u interaktivnoj računalnoj grafici, a kojim se dodatno smanjuje vrijeme izvršavanja algoritma. Naime, od samog početka smo razmatrali osvjetljenje kao funkciju u tri dimenzije, koja svakoj točki prostora preslikava neku vrijednost osvjetljenja. Međutim, sjetimo se da su objekti u virtualnoj sceni prezentirani mrežom trokuta, a svaki trokut je definiran svojim trima vrhovima. Prema tome, objekt se može promatrati kao skup vrhova, odnosno kao konačni, diskretni skup točaka. Iz ovoga slijedi da je umjesto evaluacije izraza za osvjetljenje za svaku točku površine nekog objekta, odnosno za svaki pojedini slikovni element, dovoljno izračunati osvjetljenje za svaki vrh objekata na sceni. Nakon toga, u fazi rasterizacije konačne slike, vrijednosti izračunate za pojedine vrhove se lako mogu interpolirati nad slikovnim elementima. Dakako, da bi jednadžba iscrtavanja bila potpuna, još se postavlja pitanje kako postaviti i računati funkciju distribucije reflektivnosti. Računski najnezahtjevnija jest difuzna refleksija, kod koje se upadna svjetlost raspršuje u svim smjerovima jednako, tako da je osvjetljenje tijela jednoliko po cijeloj površini. Već i ovakav model je dovoljno potpun za izračunavanje osvjetljenja koje ne djeluje potpuno nerealno. Tada jednadžba iscrtavanja poprima ovaj oblik:

Raspisivanjem gornjeg skalarnog produkta se dobiva Lambertov kosinusni zakon, zbog čega se ovaj model naziva Lambertov model osvjetljenja. Ipak, ovaj se model može lako proširiti da daje mnogo uvjerljivije rezultate, a bez drastičnog povećanja kompleksnosti. Prva ideja koja se nameće jest dodavanje konstantnog člana, za barem vrlo grubu aproksimaciju indirektnog, ambijentalnog osvjetljenja. Druga stvar koju možemo pokušati implementirati za poboljšanje kvalitete prikaza jest zrcalna refleksija, budući da ju većina tijela pokazuje bar u nekoj mjeri. Drugim riječima, zanemarit ćemo pretpostavku da je funkcija distribucije refleksije jednolika, te ćemo je pokušati definirati na prikladan način. Razvijeno je nekoliko takvih načina, čime su i definirani različiti modeli lokalnog osvjetljenja. Najpoznatiji takav jest Phongov model, koji se zasniva na opažanju da vrlo sjajne površine imaju vrlo uzak zrcalni odbljesak, čiji intenzitet opada vrlo naglo. Površine manje sjajnosti imaju širi odbljesak, koji opada sporije. Krajnosti su potpuna sažetost odbljeska u jednoj točki, ili pak rasprostiranje odbljeska preko čitave površine (ogledala). Također, može se primijetiti da zrcalni odbljesak ovisi o kutu gledanja. Shodno svemu navedenome, za svaki objekt u virtualnoj sceni se definira materijal, odnosno skup konstanti koje određuju svojstva objekta pri interakciji sa svjetlošću:

Dakle, materijal objekta određuje parametre funkcije distribucije refleksivnosti. Sama funkcija se definira na sljedeći način:

Prvi član odgovara difuznoj refleksiji, i po svom je obliku jednak Lambertovom modelu osvjetljenja. Drugi član odgovara zrcalnoj refleksiji. Budući da zrcalni odbljesak ovisi o kutu gledanja, potrebno je uvesti vektor , koji označava odnos točke promatrača prema danoj točki upada svjetlosti. Skalarni umnožak vektora iz točke na objektu (x) prema očištu i vektora smjera zrcalno reflektirane zrake, potenciran konstantom sjajnosti, daje mjeru zrcalnog osvjetljenja za danu točku. Na kraju, konačna jednadžba iscrtavanja glasi ovako:

Početni član označava konstantno ambijentalno osvjetljenje, dok izraz pod sumom odgovara difuzno – zrcalnoj refleksiji, za svako pojedino svjetlo.

Ovdje valja spomenuti da osim Phongovog, postoji još mnogo drugih lokalnih modela osvjetljenja, koji bolje ili lošije opisuju razne svjetlosne učinke i karakteristike, a koji se razlikuju po definiciji funkcije distribucije reflektivnosti: Gaussov, Beckmannov, Heidrich –Seidelov, Wardov, Cook – Torranceov model, itd. Međutim, daleko najpopularniji od svih jest varijacija gore opisanog Phongovog modela, poznata kao Blinn-Phong model osvjetljenja. Jedina promjena u odnosu na standardni Phongov model jest u vizualno gotovo neprimjetnoj aproksimaciji izraza sa zrcalnu komponentu osvjetljenja. Naime, možemo definirati vektor  na sljedeći način:

Ovaj vektor se naziva poluvektorom između vektora prema izvoru svjetlosti i vektora prema promatraču. Sada možemo u funkciji distribucije refleksivnosti promijeniti izraz za zrcalnu komponentu osvjetljenja na način da skalarni umnožak vektora smjera reflektirane zrcalne zrake i vektora gledišta, , zamijenimo skalarnim umnoškom vektora normale na površinu i poluvektora, . No, kut  će uvijek biti manji od kuta , i to točno upola manji ukoliko , ,  i  leže na istoj ravnini. Da bi krajnji rezultat ostao numerički približno jednak, potrebno je malo podesiti konstantu α, odnosno, pronaći takav α' da vrijedi . Dakle, jednadžba iscrtavanja će na kraju izgledati ovako:

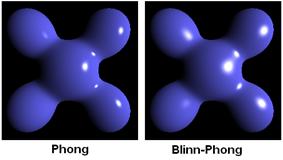
Blinn-Phongov model je efikasniji od standardnog Phongovog modela, jer je za usmjerena svjetla poluvektor potrebno izračunati samo jedamput za svako svjetlo, pa je ukupna količina posla koju je potrebno obaviti prilikom svakog iscrtavanja manja. Numerička nepreciznost do koje dolazi uslijed navedenih supstitucija je gotovo neprimjetna (slika 8.), te je ukupni dobitci na performansama potpuno opravdavaju. Zbog svojih odličnih svojstava (visoka efikasnost i brzina, realistični rezultati), Blinn-Phong model je postao toliko popularan da je standardiziran kao podrazumijevani model osvjetljenja svih poznatijih grafičkih programskih sučelja (OpenGL, Direct3D), te sklopovski implementiran na svim grafičkim karticama koje pružaju 3D ubrzanje (doduše, u novije vrijeme, grafičke kartice s programirljivim cjevovodima dopuštaju implementaciju vlastitih, proizvoljnih modela osvjetljenja).