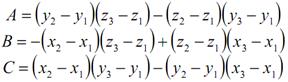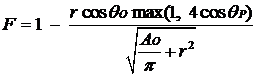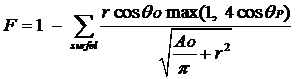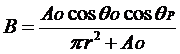Završni rad br. 38

Prisjetimo se, kod lokalnih modela osvjetljenja simulira se samo direktno osvjetljenje, dok se indirektno osvjetljenje i svi popratni učinci poput mekih sjena i pretapanja boja zanemaruju. Da scena ne bi bila premračna, obično se dodaje gruba aproksimacija indirektnog osvjetljenja, u obliku konstantnog člana jednadžbe, a taj se član naziva ambijentalna komponenta. Iako ambijentalno osvjetljenje doista jest gotovo homogeno, s tek blagim prijelazima u intenzitetu, ljudsko oko je osobito osjetljivo i na vrlo suptilne svjetlosne učinke. Tradicionalne metode simulacije globalnog osvjetljenja, opisane u prethodnom poglavlju, dobro rješavaju ovaj problem ali dostupna računalna moć tek sada postaje dostatna za početke njihove primjene u interaktivnoj računalnoj grafici. Iz tog razloga, razvijaju se različiti hibridni algoritmi, koji se baziraju na postojećim lokalnim modelima osvjetljenja i rasterizacijskim tehnikama iscrtavanja, ali uvode elemente kojima nastoje bolje aproksimirati globalne učinke osvjetljenja. Jedan od takvih algoritama jest zaklanjanje ambijenta. Naime, primijetimo da je kod lokalnih modela osvjetljenja, upravo ambijentalna komponenta razlog njihove neuvjerljivosti. Prema tome, ideja je da umjesto osvjetljavanja svakog vrha prikazanih poligona nekom konstantnom vrijednošću, koristimo neku varijabilnu vrijednost, tako da pojedini vrhovi budu tamniji, a pojedini svjetliji. Dakako, htjeli bismo postići da ta vrijednost ovisi o stupnju zaklonjenosti pojedinog vrha okolnom geometrijom, dakle da zaklonjeni vrhovi budu tamniji, a nezaklonjeni svjetliji. Ovakvo postavljanje problema dovodi do algoritma isijavanja, koji jest fizikalno točan, ali ne pruža zadovoljavajuće performanse. Algoritam zaklanjanja ambijenta, makar konceptualno vrlo sličan postupku isijavanja, pokazuje mnogo bolje performanse jer koristi fizikalno ne sasvim točan, ali mnogo efikasniji postupak. Pogledajmo detaljnije kako teče sam algoritam: na početku, stvara se pomoćna struktura na temelju geometrijskih podataka scene (popisa vrhova i poligona koje tvore). Ta pomoćna struktura sadrži takozvane elemente površine (eng. surfel, skraćeno od surface element).

Element površine jest orijentirani krug, definiran svojom točkom središta, radijusom (oplošjem), te normalom. Prednja strana elementa površine se definira kao ona strana na kojoj se nalazi normala. Ova definicija je bitna, jer prema dogovoru, svjetlost se emitira i reflektira sa prednje strane elementa površine, dok se sjene bacaju sa stražnje strane. Za svaki pojedini vrh poligona koji sačinjavaju scenu, stvara se novi element površine, i to tako da je središte tog elementa jednako poziciji njemu pripadnog vrha. Budući da geometrijski podaci obično uključuju i normale na vrhove, te se normale jednostavno mogu preuzeti za elemente površine, a u suprotnom slučaju se lako izračunaju iz poznatih vrhova poligona, koristeći sljedeću formulu:

gdje su A, B i C elementi vektora normale. Oplošje pojedinog elementa površine se računa kao zbroj trećina oplošja trokuta koji dijele promatrani vrh. Budući da su poznati svi vrhovi tih trokuta, lako se dobiju duljine njihovih bridova, pa se oplošje pojedinog trokuta može dobiti Heronovom formulom:

gdje je s poluopseg trokuta:

Jednom kad je pomoćna struktura izgrađena i popunjena svim podacima, mogu se izračunati faktori vidljivosti. Za razliku od fizikalne definicije kakva se koristi u algoritmu isijavanja, ovdje ćemo koristiti malo drugačiju, aproksimativnu definiciju. Zamislimo iznad elementa površine polukuglu. Ukoliko je taj element površine zaklonjen nekim drugim elementom, određeni dio zamišljene polukugle će biti u sjeni. Faktor vidljivosti definiramo kao postotak polukugle koji nije zaklonjen. Drugim riječima, ukoliko zbrojimo doprinose zaklonjenosti svih elemenata površine na trenutno promatrani element, onda je faktor vidljivosti tog elementa jednak jedan minus taj zbroj. Prema dogovoru, reći ćemo da je element koji biva zaklonjen primatelj, a element koji zaklanja odašiljač. 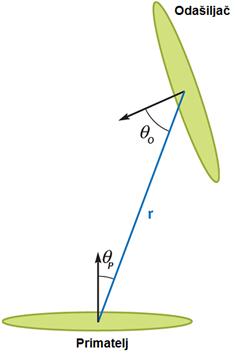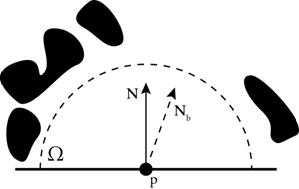Ukoliko zamislimo situaciju sa slike 13, možemo definirati vektor r koji povezuje središta odašiljača i primatelja. Kut između normale na element površine, te vektora r ćemo označiti sa θ. Sad možemo matematički formulirati definiciju faktora vidljivosti između dvaju elemenata površine:

gdje je r prethodno definirani vektor, θ_o i θ_p su odgovarajući kutevi odašiljača i primatelja, a A_o je oplošje odašiljača. Funkcija max vraća veći od dvaju argumenata, a dodana je da se ignoriraju odašiljači koji ne leže iznad primatelja (sjetimo se, samo stražnje strane elemenata površine bacaju sjene). Prema slici 13, jasno se vidi da ukoliko bi odašiljač bio ispod primatelja, kut θ_p bi bio veći od PI/2 (ili manji od –PI/2), što znači da bi kosinus tog kuta bio negativan, pa bi funkcija max vratila 1. Dakako, u slučaju da se scena sastoji od više od dvaju elemenata površine, gornji se član izračuna za svaki element u odnosu na promatrani, te se njihov zbroj oduzme od jedinice:

Međutim, gore opisanim postupkom ćemo dolaziti u situacije da promatranom elementu površine pribrojimo doprinos zaklanjanja od nekog elementa koji je i sam potpuno ili djelomično zaklonjen. To znači da će promatrani element biti previše zatamnjen, budući da element koji je i sam u sjeni, ne može bacati novu sjenu. Jedino rješenje jest provedba algoritma u dva prolaza, s time da se u drugom prolazu desni član izraza pomnoži s prethodno izračunatim faktorom vidljivosti tog elementa površine. Drugim riječima, u drugom prolazu se doprinos zatamnjenja odašiljača smanjuje, tako da se modulira faktorom vidljivosti samog tog odašiljača. Međutim, što ako je neki element površine u trostrukoj sjeni? Tada će biti potreban treći prolaz, a možda i četvrti, peti itd. Međutim, u velikoj većini praktičnih primjena se pokazalo da su dva prolaza sasvim dostatna za vrlo kvalitetne rezultate [10], kao što to ilustrira sljedeća slika:

Ovdje još valja napomenuti da se u ovom koraku algoritma obično računa i takozvana savinuta normala (eng. bent normal). Savinuta normala je vektor koji dijeli početnu točku sa pravom normalom, ali se ne nalazi pod pravim kutom nad površinom, već pokazuje u smjeru najmanje zaklonjenosti (slika 15). U postupku računanja direktnog osvjetljenja pomoću nekog lokalnog modela, tada se upotrebljava ta savinuta normala umjesto prave, čime se mogu dobiti još realističniji rezultati.

Algoritam zaklanjanja ambijenta u gore opisanom obliku pokazuje kvadratnu složenost, budući da je za svaki element površine (dakle, za svaki vrh poligona) potrebno obraditi sve ostale elemente površine. Međutim, postupak se lako može svesti na  složenost. Naime, algoritam u svome radu ne koristi direktno geometrijske podatke, već posebno generiranu strukturu elemenata površine. Ti se elementi mogu stopiti u veće elemente, a ti veći elementi se mogu stopiti u još veće elemente, itd. Samo „stapanje“ elemenata se vrši tako da središte elementa-roditelja postane aritmetička sredina središta elemenata-djece. Isto tako, normala roditelja se računa kao aritmetička sredina normala djece, dok je oplošje roditelja jednaka zbroju oplošja djece. Dakle, moguće je složiti hijerarhiju elemenata površine, od najgrubljeg prikaza do najfinijeg, što će u memoriji računala biti prikazano kao stablo. Korijeni tog stabla će biti najveći i najgrublji elementi površine, dok će listovi biti najmanji i najfiniji elementi. Pojedini čvorovi će biti negdje između ta dva ekstrema. Ovo si možemo predstaviti kao skup slojeva, takvih da se u najvišem sloju nalazi najmanji broj elemenata, u sljedećem sloju malo veći broj elemenata, u sljedećem još veći, i tako do zadnjeg sloja koji posjeduje najveći broj elemenata. Algoritam tada započinje rad koristeći prvi sloj. Tek ukoliko su dva elementa površine dovoljno blizu jedan drugome, algoritam će prijeći u niži, detaljniji sloj. Rezultat jest taj, da će udaljeni predmeti imati mutne i neprecizne sjene, dok će bliži predmeti pokazivati mnogo detaljnije sjene. Ovaj postupak je opravdan, budući da su ti detalji i blagi prijelazi u sjenama ionako slabo zamjetni osim na vrlo malenim udaljenostima, dok su na većim udaljenostima potpuno nezamjetni.

Upravo opisani postupci sačinjavaju prvu i glavnu fazu ovog algoritma, nakon koje je za svaki vrh objekata koji tvore scenu definirana zasebna ambijentalna komponenta osvjetljenja, umjesto konstantne vrijednosti za čitavu scenu kakvu standardno koriste lokalni modeli osvjetljenja. Međutim, ta je ambijentalna komponenta dobivena isključivo promatranjem zaklonjenosti pojedinih vrhova (od čega potječe i naziv samog algoritma), no ne i indirektnog osvjetljenja koje nastaje refleksijom svjetla između samih objekata. Drugim riječima, dobili smo meke sjene, ali ne i učinke poput pretapanja boja. Ipak, pokazuje se da se algoritam može relativno jednostavno proširiti [10], tako da uključuje i zadovoljavajuću aproksimaciju indirektnog osvjetljenja. Ta se aproksimacija bazira na prijenosu zračenja između pojedinih elemenata površine. Naime, ako se prisjetimo algoritma isijavanja, računali smo faktore vidljivosti između parova poligona, te koristili te faktore za izračun prijenosa zračenja. Budući da i u algoritmu zaklanjanja ambijenta također koristimo vrlo sličan koncept, moguće je proširiti algoritam tako da dodatno izračunava i prijenos zračenja. Ovo se postiže tako da za svako svjetlo na sceni, obradimo elemente površine (koristeći hijerarhiju elemenata za ubrzanje). Ta obrada se sastoji od toga da se za prednju stranu svakog direktno osvjetljenog elementa površine izračuna maksimalan iznos reflektiranog zračenja s obzirom na njemu susjedne elemente. Pritom možemo koristiti sljedeću aproksimacijsku formulu:

gdje je A_o oplošje odašiljača, r vektor između središta odašiljača i primatelja, a θ_o i θ_p kutevi vektora r s obzirom na normale odašiljača i primatelja. Dakako, maksimalan prijenos isijavanja u većini slučajeva neće biti ostvaren, budući da će velik broj vrhova biti barem djelomično zaklonjen. Zbog toga je dobiveni iznos zračenja potrebno modulirati s prethodno izračunatim faktorom vidljivosti. Jednom kad je izlazno isijavanje izračunato, potrebno ga je pomnožiti s bojom odašiljača, te pridodati primatelju. Nakon ovog koraka, može se primijetiti učinak pretapanja boja. Međutim, ovdje se javlja sličan problem kao i kod klasičnog algoritma isijavanja. Naime, samo jednim prolazom, riješili smo problem jednostruko odbijenog indirektnog osvjetljenja. Dodatnim prolazima možemo propagirati zračenje i kroz višestruka odbijanja, no već su i dva prolaza dostatna da globalni učinci osvjetljenja postanu zamjetljivi. Budući da je ovaj algoritam namjenjen za korištenje u interaktivnoj računalnoj grafici, indirektno osvjetljenje sačinjeno od jednostrukih i dvostrukih difuznih interrefleksija predstavlja sasvim prihvatljiv kompromis između kvalitete i performansi, i značajno je unaprijeđenje u odnosu na konstantno ambijentalno osvjetljenje. Dobar primjer pokazuje donja slika. Sasvim lijevo vidimo scenu osvjetljenu standardnim, lokalnim modelom osvjetljenja. U sredini je rezultat proširenog algoritma zaklanjanja ambijenta s jednim prolazom, dok je krajnje desno rezulat dvaju prolaza tog algoritma.