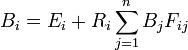Završni rad br. 38

Jedna od najstarijih skupina algoritama u računalnoj grafici uopće su takozvani algoritmi praćenja zrake. Osnovna ideja je vrlo jednostavna – principi i zakonitosti geometrijske optike se direktno simuliraju računalom. Dakle, pretpostavlja se da izvori svjetlosti emitiraju svjetlost u zrakama, koje se mogu predstaviti pravcima (ili linijskim segmentima). Zatim je potrebno za svaku od tih zraka odrediti da li presijeca neki od objekata na sceni, te po potrebi generirati novu zraku (reflektiranu i/ili refraktiranu). Na kraju, zrake koje upadaju na virtualnu kameru, odnosno, na ravninu projekcije, definiraju slikovni element na koji upadaju, a pritom se za izračun samih doprinosa svjetlosti za pojedinu zraku koristi neki od lokalnih modela osvjetljenja. Na ovaj način se na zaslonu generira 'pogled' u virtualnu scenu. U opisanom postupku je moguće uvesti nekoliko varijacija, pa se tako razlikuje i nekoliko srodnih algoritama. Osnovna varijacija u odnosu na standardni postupak jest u praćenju zrake u obrnutom smjeru; umjesto praćenja pojedine zrake svjetlosti od izvora, preko objekata na sceni do kamere, zraka se prati od kamere, prema objektima na sceni. Naime, možemo primjetiti da u gotovo svim slučajevima, većina zraka svjetlosti koje izlaze iz izvora uopće ne dotiču okolne predmete, ili ne dotiču kameru. Prema tome, ukoliko pratimo zrake iz kamere, sigurno ćemo morati računati samo ono što nam je potrebno za danu scenu, čime drastično povećavamo efikasnost algoritma. Ovdje valja napraviti razliku između algoritma bacanja zraka (ray casting)  i algoritma praćenja zraka (ray tracing). Naime, oba algoritma prate zrake od kamere do objekata na sceni, no algoritam bacanja zraka se zaustavlja kad pronađe sjecište trenutne zrake s najbližim objektom na sceni, dok algoritam praćenja zrake u tom trenutku generira nove zrake (prema zakonima geometrijske optike), te se rekurzivno poziva i za te nove zrake. Očito, prvi algoritam ne može simulirati učinke globalnog osvjetljenja, ali je mnogo brži, te se koristio u počecima interaktivne računalne grafike (primjerice, u igri Wolfenstein 3D). Drugi algoritam je sposoban doći mnogo bliže potpunom rješenju jednadžbe iscrtavanja, ali je mnogo sporiji. Dodatna optimizacija koja se obično koristi u algoritmu praćenja zrake su takozvane zrake sjene (shadow rays). Naime, kada se pronađe sjecište trenutne zrake sa najbližim objektom na sceni, prije stvaranja reflektirane i/ili refraktirane zrake (već prema svojstvima materijala), provjerava se da li je presječena površina (poligon) usmjeren prema nekom izvoru svjetlosti. Ukoliko jest, stvara se zamišljena zraka sjene, usmjerena od površine prema izvoru. 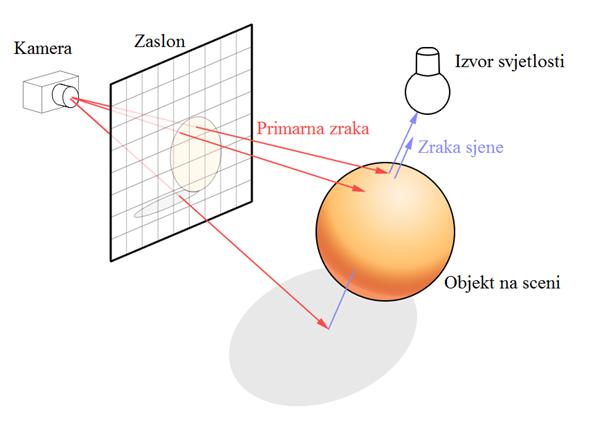Ukoliko tu zraku presijeca neki neprozirni objekt (dakle, ako zraka sjene presijeca neku drugu neprozirnu površinu), tada je površina koju ispitujemo u sjeni, te nije potrebno stvarati reflektiranu i/ili refraktiranu zraku, što znači da nije potrebno ulaziti u novu dubinu rekurzije. Na priloženoj ilustraciji (Slika 9) vidimo primjer rada algoritma. Promatramo tri primarne zrake koje pratimo iz kamere. Gornje dvije upadaju na kuglu, te njihove pripadne zrake sjene ne presijecaju nikakve druge površine na putu do izvora svjetlosti. Dakle, u tim bi se slučajevima generirale nove zrake, nastale refleksijom i refrakcijom, te bi se algoritam rekurzivno pozvao. Za treću primarnu zraku, koja upada na pod ispod objekta, zraka sjene presijeca neprozirnu površinu objekta, te se algoritam zaustavlja.

Postoji nekoliko nadogradnji na ovaj temeljni algoritam koje se baziraju na Monte Carlo (probabilističkim) tehnikama, od kojih je temeljni predstavnik algoritam praćenja puta. Postupak je vrlo sličan standardnom, samo se zrake generiraju na način da prate slučajno odabrani put. Dakle, u svakoj točki presjeka zrake sa objektom na sceni, generira se nova zraka, ali u nekom slučajno odabranom smjeru. Postupak se ponavlja dokle god postoji presjek promatrane zrake sa nekim objektom na sceni, a izračunati svjetlosni doprinosi se zbrajaju po dubinama rekurzije. Mnogo napredniji probabilistički postupak jest algoritam preslikavanja fotona (photon mapping), koji zajedno sa standardnim tehnikama praćenja zrake pruža veoma realistične rezultate, s ispravnim efektima kaustike i mekim sjenama. Ovaj se algoritam sastoji od dvije faze. U prvoj fazi se konstruira spremnik fotona, a u drugoj fazi se iscrtava sama scena. Spremnik fotona se popunjava tako da se uzduž zraka svjetlosti odašilju fotoni. Ukoliko zraka presijeca neki objekt, njeni se fotoni pohranjuju u spremnik, te se izvršava neka od sljedećih akcija: generiranje reflektirane i/ili refraktirane zrake (rekurzivno ponavljanje algoritma), apsorpcija (kraj algoritma). Ove se akcije izvršavaju slučajnim odabirom, a vjerojatnost odabira pojedine akcije je definirana materijalom objekta. U drugoj fazi, scena se iscrtava klasičnim postupkom praćenja zrake, no umjesto korištenja nekog modela lokalnog osvjetljenja za izračun svjetlosnih doprinosa, koristi se prethodno generiran spremnik fotona za proračun funkcije distribucije refleksivnosti.

Opisani algoritmi se svi baziraju na osnovnom principu direktne simulacije zakonitosti (geometrijske) optike. No, postoji i alternativni pristup, koji se bazira na simulaciji toplinskog zračenja (algoritam isijavanja, eng. radiosity). Naime, prisjetimo se da kod difuzne refleksije, tijelo isijava svjetlost jednoliko preko čitave svoje površine – baš kao i toplinu! Sam algoritam funkcionira na sljedeći način: za svaki par poligona koji sačinjavaju cjelokupnu scenu, definira se faktor vidljivosti. Taj faktor govori u kojoj mjeri jedan poligon „vidi“ drugoga, a matematički se izražava kao mjera radijacije koja izlazi iz jedne površine, a upada na drugu. Postoji nekoliko načina pomoću kojih se mogu dobiti ti faktori, od kojih je najjednostavnije korištenje polukocaka. U ovom kontekstu, pod pojmom „polukocka“ se podrazumjeva takva kocka, koja je presječena nekom ravninom paralelnom s nekom stranicom te kocke, i to tako da se mreža dobivene polukocke sastoji od jednog kvadrata, te četiri pravokutnika sa odnosom stranica 2:1.

Takva polukocka se centrira s obzirom na promatrani poligon, te se cijela scena iscrta pet puta, za svaku stranicu polukocke, i to tako da gledište leži na normali stranice. Na taj način se dobiju projekcije okolnih poligona na promatrani poligon, te se može izračunati mjera preklapanja površina tih poligona – upravo ta veličina jest faktor vidljivosti. Jednom kad izračunamo faktore vidljivosti za sve parove poligona, možemo upotrijebiti formulu za ukupno zračenje površine, koja kaže da je ukupno zračenje jednako zbroju emitiranog zračenja, i reflektiranog zračenja:

gdje je:

Ukoliko pretpostavimo savršeno difuznu refleksiju, takvu da se svjetlost odbija savršeno jednoliko u svim smjerovima, lako možemo provesti diskretizaciju i pretvoriti gore napisanu integralnu jednadžbu u sumacijsku:

U ovom obliku, jednadžba se lako može izračunati za svaki poligon, te se „zračenje“ nekog poligona može jednostavno interpretirati kao njegova svjetlina, odnosno, boja. Međutim, pošto je svjetlina svakog poligona definirana zračenjima njemu vidljivih poligona, a na početku su zračenja svih poligona koji nisu izvori svjetla jednaka nuli, možemo zaključiti da će algoritam u gore opisanom obliku osvjetljavati samo one poligone na koje upada osvjetljenje direktno iz izvora, te njima susjedne poligone koje algoritam obradi poslije tih direktno osvijetljenih poligona. Dakle, dešava se situacija da poligoni koji bi trebali biti osvijetljeni svjetlošću reflektiranom od nekog poligona koji je direktno osvijetljen, nisu osvijetljeni čisto iz razloga što algoritam u trenutku njihove obrade još nije bio stigao obraditi direktno osvijetljeni poligon, pa je njegovo zračenje ostalo na nuli! Rješenje je vrlo jednostavno – jedna iteracija algoritma nije dovoljna, stoga se provodi dodatna. No, i u drugoj iteraciji se ponovno javlja isti problem, budući da promjenom zračenja indirektno osvijetljenih poligona, oni sami postaju sekundarni izvori svjetla. Također, ti sekundarni izvori svjetlosti mogu opet osvjetljavati neke nove poligone, koji i sami postaju novi izvori svjetlosti, što dovodi do zaključka da je potreban beskonačan broj iteracija algoritma. Međutim, tome ipak nije tako, budući da s brojem iteracija indirektni doprinosi osvjetljenju značajno opadaju, dok napokon ne postanu zanemarivi. Taj prag zanemarivosti ovisi o karakteristikama scene, no za većinu praktičnih primjena, osam do šesnaest iteracija je sasvim zadovoljavajuće. Algoritam, zbog svoje prirode, veoma dobro simulira efekte globalnog osvjetljenja kao što su pretapanje boja i meke sjene, no nažalost, prisutno je fundamentalno ograničenje na isključivo difuzno osvjetljenje. Zanimljiva je komplementarnost algoritma isijavanja i algoritma praćenja zrake; prvi dobro simulira efekte poput difuznih interrefleksija i mekih sjena, ali se ne može koristiti za zrcalnu refleksiju, dok drugi točno simulira zrcalnu refleksiju i oštre sjene, ali difuzna refleksija i meke sjene su teže za izvesti. U obliku u kojem je predstavljen, algoritam isijavanja ima kvadratnu složenost s obzirom na broj poligona od kojih je sačinjena scena. Međutim, postoje razna unaprijeđenja osnovnog algoritma, kojima se smanjuje vremenska kompleksnost – primjerice, korištenjem binarne podjele prostora, problem određivanja vidljivosti poligona se može svesti na logaritamsku kompleksnost. Nadalje, samo računanje faktora vidljivosti pomoću polukocaka je također vremenski dosta zahtjevno, budući da se cjelokupna scena mora iscrtati pet puta. U općenitom slučaju, ti se faktori zbog deformacije objekata na sceni mogu mijenjati prilikom svakog iscrtavanja, pa se svaki put moraju nanovo i izračunavati, no u većini stvarnih situacija, nagle i potpune promjene vidljivosti se dešavaju vrlo rijetko. To znači da između pojedinih iscrtavanja scene postoji značajna kohezija između faktora vidljivosti, a to se svojstvo može iskoristiti za dodatnu optimizaciju algoritma [4].

Međutim, uz sve optimizacije, niti algoritmi isijavanja, niti algoritmi praćenja zrake sve do nedavno nisu bili upotrebljivi u interaktivnoj računalnoj grafici, iz jednostavnog razloga nedostatka računalne moći. No, kako dostupna računalna moć pokazuje tendenciju stabilnog rasta, tako se javlja i ideja interaktivnog globalnog osvjetljenja. U tom kontekstu, postoji nekoliko različitih pristupa, koji se ili razvijaju u sklopu trenutno prevladavajućih rasterizacijskih tehnika, ili na temelju postupaka praćenja zrake i/ili isijavanja. Algoritam praćenja zrake je posebice zanimljiv u tom pogledu, jer ga je moguće veoma lako paralelizirati. Naime, za svaki slikovni element zaslona, posebno se vrši proračun osvjetljenja, i to neovisno o svim drugim slikovnim elementima. To znači da se svi slikovni elementi mogu obrađivati istovremeno! Ovo svojstvo je izuzetno zanimljivo s obzirom na tendenciju rasta broja jezgri procesora – teoretski, s n dostupnih jezgri, iscrtavanje bi trebalo biti n puta brže. Prema tome, već i danas dostupnom tehnologijom bi se trebale moći postići gotovo interaktivne performanse, barem na igrama prethodne generacije. Potvrdu ovakvom razmišljanju daje Intelova istraživačka grupa vođena Danielom Pohlom, prilagodivši komercijalnu igru Quake IV, izdanu krajem 2005. godine, za rad s eksperimentalnim paketom za praćenje zrake (razvijenim od strane spomenute grupe) [6]. Rezultati su veoma bliski očekivanima: dvojezgreni sustav je ostvarivao otprilike dvije slike u sekundi, četverojezgreni 3.8, a 16-jezgreni 15.2 (taj je sustav emuliran povezivanjem četiriju četverojezgrenih procesora). Budući da su četverojezgreni procesori već danas široko dostupni, nije nezamislivo da će za nekoliko godina softversko iscrtavanje u stvarnom vremenu postupkom praćenja zrake biti sasvim izvedivo na prosječnim računalima. S druge strane, grafički procesori već danas posjeduju nekoliko stotina procesnih jedinica (ATI Radeon HD3870 X2 ih posjeduje ukupno 640), pa jednostavnom računicom dobivamo da bi praćenje zrake implementirano na grafičkom podsustavu bilo barem 30 do 50 puta brže nego na glavnom procesoru. Dakako, postavlja se pitanje kako izvesti algoritam praćenja zrake na sklopovlju dizajniranom za rasterizaciju. No, grafički procesori već neko vrijeme nisu ograničeni isključivo za obradu grafike. Razvojem jezika za sjenčanje visoke razine (sintakse usporedive sa C jezikom) za upravljanje programirljivim cjevovodom grafičkih procesora, oni postaju gotovo autonomni podsustav opće namjene, što je dovelo do stvaranja posebnog termina „općenamjenski grafički procesor“ (eng. General Purpose Graphics Processing Unit, GPGPU). Tvrtka nVidia, jedan od vodećih razvijatelja grafičkih procesora, je otišla korak dalje, te predstavila prevodilac za programski jezik C, koji generira instrukcije izvršive na nVidijinim grafičkim procesorima. Ova se tehnologija naziva Compute Unified Device Architecture (CUDA), te iako postoje neka ograničenja (rekurzivne funkcije nisu podržane), većina bitnih mogućnosti koje pruža glavni procesor, poput slobodnog dodjeljivanja memorije, jest podržana. To znači da je teoretski moguće napisati višedretveni algoritam praćenja zrake u C programskom jeziku, te ga prevesti za izvođenje na grafičkom procesoru. Također, i tvrtka ATI posjeduje sličnu tehnologiju koju nazivaju Close To Metal (CTM), koja je dostupna na ATI grafičkim karticama. Budući da je riječ o prilično novim tehnologijama čiji je razvoj tek započeo, konkretnih primjera njihove upotrebe još nema, no njihov je potencijal nemjerljiv. Osim klasičnog postupka praćenja zrake, moguće bi bilo implementirati i neki napredniji dodatak, kao što je to preslikavanje fotona. Konkretno, implementacije takvog algoritama su već ostvarene na grafičkim procesorima, koristeći postojeće jezike za sjenčanje [9]. Algoritam isijavanja bi imao tek djelomičnu korist od paralelne arhitekture grafičkih kartica, budući da se njegove iteracije ionako moraju izvršavati sekvencijski, a i unutar pojedine iteracije, vrijednost zračenja pojedinog poligona ovisi o zračenjima svih ostalih poligona. Jedina faza algoritma pogodna za paralelizaciju jest određivanje vidljivosti okolnih poligona za dani poligon.

Drugi značajan smjer razvoja interaktivnog globalnog osvjetljenja su postupci koji se i dalje baziraju na rasterizaciji, no proširuju opisane lokalne modele osvjetljenja tako da zamjenjuju određene aproksimacije fizikalno točnijim proračunima, približavajući se tako pravim globalnim modelima osvjetljenja. Ovo područje računalne grafike se intenzivno razvija, tako da se u ovoj skupini razlikuje veliko mnoštvo algoritama. U nastavku će biti opisana dva karakteristična postupka  u svom osnovnom obliku, a riječ je o zaklanjanju ambijenta (eng. ambience occlusion), te predizračunatom prijenosu zračenja (eng. precomputed radiance transfer).