|
Testiranje
je li došlo do sudara između dva tijela određuje se na način da
se za svaki vrh testira je li unutar ili izvan tijela. Na taj način
se neće detektirati svi sudari poput sudara između dva brida kada
se vrhovi brida nalaze izvan tijela s kojim se traži sudar. Kada se
tijelo sastoji od velikog broja trokuta greška zbog zanemarenih sudara
između bridova biti će mala, no ukoliko se traži sudar za tijelo
s malim brojem trokuta greška će biti prevelika da bi zanemarili sudare
između bridova. Na primjer, za detekciju sudara između dvije kocke
koje imaju samo 12 trokuta greška je prevelika pa je potrebno detektirati
sudare između bridova. Sudari između bridova se detektiraju na način
da se na svaki brid doda određeni broj točaka, ovisno o tome koliko
preciznu simulaciju želimo (za sudar između dvije kocke iste veličine
dovoljno je dodati dva do tri vrha). Za svaku točku na bridu vrši
se detekcija sudara i od svih tih točaka za točku sudara se uzima
samo ona točka koja se nalazi najdublje unutar drugog tijela.
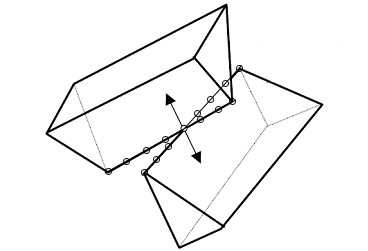
Slika 6. Sudar između dva brida
Određivanje predznaka
Nalazi li
se točka unutar konkavnog tijela ili izvan njega može se odrediti
na mnogo načina. Jedan od jednostavnijih načina je bacanjem zrake
iz točke i određivanja sjecišta zrake s mrežom poligona. Ukoliko
je zraka presjekla mrežu neparan broj puta točka je unutar tijela.
Problem kod bacanja zrake je kada zraka siječe više trokuta u istoj
točci (kada siječe bridove ili vrhove) pa je potrebno ta sjecišta
brojati kao jedno. Zbog toga će se u ovom radu za određivanje predznaka
koristiti metoda predstavljena u [3].
Prvo je potrebno
odrediti točku na površini tijela x koja je najbliža točki p za koju želimo
odrediti predznak. Normala nu točki x jednaka je normali poligona kojem pripada (osim za točke na bridovima
i vrhovima). Sada je jednostavno za odrediti je li točka unutar ili
izvan tijela a to je skalarnim produktom normale n i
vektora r=p-x.
Ukoliko je produkt pozitivan točka je izvan tijela a inače je u tijelu.
Međutim za bridove i vrhove normala nije definirana te se lako može
pokazati da postoje slučajevi kod kojih je skalarni produkt s nekim
normalama poligona koji se sjeku u vrhu pozitivan dok je s drugim negativan.
Primjer takvog slučaja vidi se na slici 7.
Slika
7. Skalarni umnožak r=p-x s jednom normalom daje pozitivan rezultat a s drugom negativan.
Potrebno
je odrediti normalu kod koje će skalarni produkt dati ispravan rezultat.
Takva normala nazvat će se pseudo normala. Pseudo normala bi
se mogla izračunati kao srednja vrijednost svih normala poligona u
vrhu, kao kod računanja normale prilikom Gouraud-ovog sjenčanja, no
i tada se mogu pronaći slučajevi kod kojih skalarni produkt ne daje
ispravan rezultat. Ispravna normala odredit će se zbrojem svih normala
poligona pri čemu će težina svake normale ovisiti o veličini kuta
pod kojim određeni poligon sudjeluje u vrhu. Tako za normalu na bridu
između dva poligona i i j vrijedi:
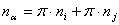 |
(3.1) |
Dok za normalu u vrhu vrijedi:
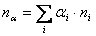 |
(3.2) |
Za trokut određen vrhovima
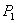 , , 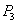 , , 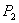 koji vrhom
koji vrhom 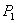 sudjeluje u određivanju normale težina sudjeluje u određivanju normale težina
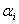 normale normale 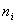 jednaka je kutu između vektora jednaka je kutu između vektora
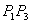 i i 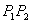 . .
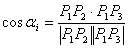 |
(3.3) |
Prilikom
određivanja udaljenosti točke od tijela potrebno je odrediti udaljenost
točke od svakog trokuta, udaljenost od tijela jednaka je najmanjoj
od svih tih udaljenosti. Osim udaljenosti potrebno je odrediti i točku
na trokutu koja je najbliža za traženu točku te normalu. Da bi se
to odredilo potrebno je pronaći regiju u koju se projicira tražena
točka a to će se sve odrediti prilikom određivanja udaljenosti točke
od trokuta (Slika 8.).
Slika
8. Sedam različitih Voronoi-evih regija ravnine u kojoj se nalazi
trokut
Udaljenost točke od trokuta
Udaljenost
točke od trokuta nije jednostavno za izračunati kao što bi se moglo
pomisliti na prvi pogled. To je zbog toga što postoji mnogo različitih
slučajeva. Točka može biti najbliža ravnini trokuta, najbliža bridu
trokuta ili najbliža vrhu trokuta.
Metoda određivanja udaljenosti koja se koristi u ovom radu dobro je opisana u [4].
Slika
9. Određivanje udaljenosti točke od trokuta
Normala 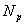 od trokuta od trokuta 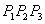 se može izračunati kao:
se može izračunati kao:
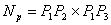 |
(3.4) |
Kut između normale 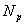 i
i 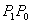 je:
je:
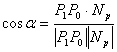 |
(3.5) |
Udaljenost točke 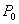 do njene projekcije na ravnini trokuta
do njene projekcije na ravnini trokuta 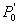 je:
je:
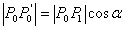 |
(3.6) |
Vektor 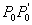 iznosi:
iznosi:
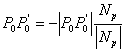 |
(3.7) |
Sada se može odrediti
projicirana točka 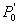 : :
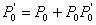 |
(3.8) |
Da bi se odredilo je
li projicirana točka unutra ili izvan trokuta i ako je izvan kojem
je bridu ili vrhu najbliža potrebno je odrediti položaj točke u odnosu
na tri vektora 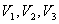 koji predstavljaju simetrale kutova:
koji predstavljaju simetrale kutova:
Slika
10. Određivanje položaja točke u odnosu na simetrale kutova
Ako je 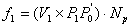 ,
i ,
i 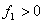 kažemo da se
kažemo da se 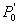 nalazi iznad vektora
nalazi iznad vektora 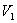 (ili da se
(ili da se 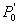 nalazi suprotno od smjera kazaljke na satu u odnosu na
nalazi suprotno od smjera kazaljke na satu u odnosu na 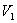 ).
Na isti način se mogu i izračunati ).
Na isti način se mogu i izračunati 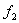 i
i 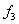 .
Koristeći .
Koristeći 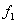 , , 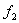 i
i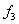 može se odrediti položaj točke
može se odrediti položaj točke 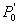 u odnosu na
u odnosu na 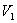 , , 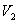 i
i 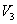 .
Ako se .
Ako se 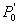 nalazi ispod
nalazi ispod 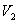 i
iznad i
iznad 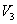 točka je unutar trokuta ako je:
točka je unutar trokuta ako je:
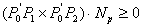 |
(3.10) |
Slijedi da je udaljenost
točke od trokuta jednaka 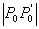 . .
Ukoliko je izraz (3.10)
neistinit točka je izvan trokuta i potrebno je odrediti je li najbliža
bridu ili vrhu.
Smjer od 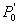 (projekcija (projekcija 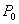 na ravninu) prema
na ravninu) prema 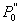 (projekcija
(projekcija 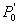 na
brid) jednak je: na
brid) jednak je:
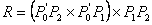 |
(3.11) |
Kut između vektora 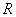 i
i 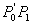 je:
je:
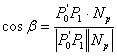 |
(3.12) |
Udaljenost točke 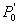 do njene projekcije na bridu je:
do njene projekcije na bridu je:
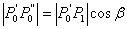 |
(3.13) |
Vektor 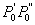 iznosi:
iznosi:
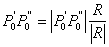 |
(3.14) |
Sada se može odrediti
projicirana točka na bridu 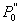
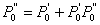 |
(3.15) |
Neka je:
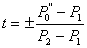 |
(3.16) |
Gdje je predznak negativan
ukoliko je 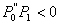 . .
Ako je 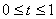 , , 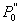 je između
je između 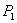 i
i 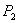 ,
znači da je točka ,
znači da je točka 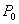 najbliža bridu
najbliža bridu 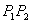 .
Udaljenost .
Udaljenost 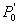 od brida
od brida 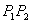 je
je 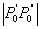 izračunata u (3.13) a udaljenost
izračunata u (3.13) a udaljenost 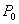 od
brida od
brida 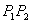 je
je 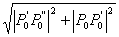 . .
Ako je 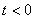 , , 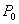 je najbliža točki
je najbliža točki 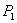 ,
i udaljenost ,
i udaljenost 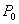 od trokuta je
od trokuta je 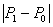 . .
Ako je 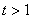 , , 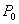 je najbliža točki
je najbliža točki 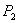 ,
i udaljenost ,
i udaljenost 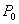 od trokuta je
od trokuta je 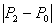 . .
Na sličan
način se izračuna udaljenost točke od trokuta za slučaj kada se 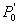 nalazi ispod
nalazi ispod 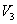 i iznad
i iznad 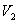 ,
te slučaj kada se ,
te slučaj kada se 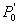 nalazi ispod
nalazi ispod 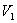 i iznad
i iznad 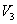 . .
|


