Kod rješavanja sudara izvršeno je nekoliko iteracija tako da su se tijela odbila jedna od drugih nekoliko puta i dobilo se uvjerljivo ponašanje tijela. Iako možda i nisu riješeni svi sudari pa se tijela i dalje sudaraju svejedno se ažuriraju brzine i krene se na rješavanje kontakata. Algoritam za rješavanje kontakata jednak je algoritmu za rješavanje sudara osim što se za koeficijent elastičnosti koristi vrijednost nula tj. sudari će se tretirati kao da su neelastični. Sudare je ispravno tretirati na ovaj način zbog toga što se tijela koja se mnogo puta sudaraju unutar kratkog vremenskog intervala vrlo brzo gube energiju i prestaju se gibati.

  Isto kao i kod detektiranja sudara kontakti se detektiraju tako da se privremeno odrede novi položaji tijela koje bi poprimili u sljedećem vremenskom koraku i zatim se testiraju na sudare. Tako za tijela koja stoje na podlozi ništa se neće detektirati prilikom detekcije sudara ali nakon što im se promjeni brzina utjecajem gravitacije detektirat će se kontakti.

Koeficijent elastičnosti

  Za svaki vrh koji se nalazi unutar drugog tijela označi se da je u kontaktu. Uzme se onaj vrh koji se nalazi najdublje unutar drugog tijela i giba se prema drugom tijelu i na njega se primjeni neelastični impuls. Za novu poziciju tijela ponovo se uzme vrh s najvećom dubinom sudara i na njega se primjeni neelastični impuls. Postupak se ponavlja sve dok se svi vrhovi barem jednom ne nađu izvan tijela ili se udaljavaju od tijela. 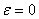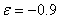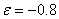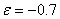Pri tome se za bolju preciznost umjesto primjenjivanja potpunog neelastičnog impulsa za svaki vrh u kontaktu postepeno se u svakom koraku iteracije upotrebljavaju impulsi , , sve do 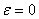u zadnjem koraku iteracije, čime se tijelo postepeno usporava umjesto da se potpuno zaustavi. Negativni koeficijent elastičnosti označava to da će se tijelo samo usporiti umjesto da promjeni smjer.

Propagirajući model

  Veliki problem se javlja kada imamo tijela koja stoje jedno na drugom tako da će biti potrebno izvršiti više iteracija kako bi se svi kontakti detektirali. Takav način rješavanja kontakata naziva se propagirajući model za razliku od simultanog rješavanja kontakata.

  Slika 16. Propagirajući model

  Neka za primjer imamo kocke koje stoje jedna na drugoj. Pod utjecajem gravitacije sve kocke će početi padati istom brzinom tako da će se samo za kocku na dnu detektirati kontakt sa podlogom. Rješavanjem kontakta kocka na dnu će doći u stanje mirovanja i u sljedećoj iteraciji će se detektirati kontakt između te kocke i kocke koja stoji na njoj. Sada će se riješiti kontakt kao neelastični sudar tako da se gornja kocka neće zaustaviti nego će se samo duplo sporije gibati. Da bi stvar bila još gora sada će se i donja kocka nastaviti gibati i biti će potrebno ponovo riješiti sudar između nje i podloge kako bi se zaustavila. Vidimo da tijela sporo konvergiraju ispravnom rješenju pa je potrebno mnogo iteracija kako bi se dobilo uvjerljivo ponašanje tijela.

Kontaktni graf

  Kako bi se povećala efikasnost rješavanja kontakata potrebno je konstruirati kontaktni graf. Pomoću grafa će se odrediti redoslijed kojim će se rješavati kontakti između tijela. Željeni redoslijed rješavanja kontakata je u smjeru od podloge i drugih statičkih objekata prema vrhu. Nakon određivanja novih brzina tijela zbog utjecaja gravitacije za svako tijelo se odredi njegova nova pozicija u sljedećem vremenskog koraku, zatim se odrede svi kontakti između tog i ostalih tijela. Za svaki se kontakt u graf doda usmjereni brid koji pokazuje od trenutnog tijela prema tijelu s kojim je detektiran kontakt. Tijela je potrebno sortirati a to se postiže pretraživanjem grafa u dubinu. Tako se za naslagane kocke dobije sortirana lista kocaka od dna prema vrhu kao što pokazuje sljedeća slika.

  Slika 17. Konstrukcija kontaktnog grafa

  Za usmjereni aciklički graf G sortiranje je prilično jednostavno. Sljedećim algoritmom stvara se sortirana lista čvorova:  

DFS(G)
{
      za svaki čvor u iz G
            u.visited = false; 

      za svaki čvor u iz G
            ako (!u.visited) DFS-Visit(u);
} 

DFS-Visit(u)
{
      u.visited = true; 

      za svaki čvor v iz u.čvoroviDjeca
            ako (!v.visited) DFS-Visit(v); 

      dodaj čvor u u listu čvorova;
} 

  Za složenije slučajeve poput skupa domino pločica složenih u krug gdje svaka leži na onoj ispod sebe u jednu razinu se stavi podloga a sve pločice se stave u drugu razinu. Znači sva tijela koja međusobno imaju cikličku vezu postavljaju se u istu razinu kao što se vidi na slici 18.

  Slika 18. Rješavanje cikličke veze u kontaktnom grafu

Sortiranje grafa koji ima cikličke veze obavlja se na sljedeći način:

  1. izračunaj inverz grafa GT.
  2. pozovi DFS(GT) kako bi se odredio redoslijed izlaza iz čvorova.
  3. pozovi DFS(G) s time da se početni čvorovi u glavnoj petlji od DFS uzimaju obrnutim redoslijedom od redoslijeda izračunatog u koraku 2.
  4. Za svaki novi čvor u glavnoj petlji od DFS broj razine povećaj za jedan, a sve čvorovi do kojih se dolazi rekurzivnim pozivom DFS-Visit označi trenutnim brojem razine.

Za primjer na slici 17. Dobije se sljedeći kontaktni graf G.

Inverz GT grafa G dobije se promjenom smjera svih veza unutar grafa.

Pretraživanjem u dubinu inverznog grafa GT u koraku 2 dobije se sortirana lista (4,3,5,2,1). U koraku 3 graf G se pretražuje obrnutim redoslijedom od redoslijeda zapisanog u listi pa se tako prvo čvor 1 stavi u prvu razinu, zatim se u sljedeću razinu stave čvorovi 2,3,4 i u zadnjoj razini čvor 5 čime dobijemo sortirane čvorove po razinama kao na slici 18. Dokaz da je prethodni algoritam ispravan te njegov detaljniji opis mogu se pronaći u [10] i [11].

Propagiranje šoka

  Bez obzira na korištenje kontaktnog grafa svejedno će biti potreban dosta veliki broj iteracija da bi se dobila uvjerljiva simulacija. No neovisno o tome koliki je broj iteracija korišten nakon nekog vremena će se primijetiti da tijela propadaju jedno u drugo pogotovo za simulaciju većeg broja tijela naslaganih jedno na drugo. Da bi se riješio taj problem koristit će se metoda propagiranja šoka [1]. To znači da će se nakon rješavanja kontakata izvršiti još jedna iteracija na poseban način. Nakon rješavanja kontakata u svakom nivou grafa za sva tijela u tom nivou masa se postavlja na beskonačnu vrijednost (matrica sudara se postavi na nulu). Sada se vidi prava svrha kontaktnog grafa. Ako se tijelo kojem je masa postavljena na beskonačnu vrijednost nađe u sudaru s nekim tijelom iz višeg nivoa njegova brzina se neće promijeniti pod utjecajem impulsa nego će tijelo iz višeg nivoa dobiti duplo veću brzinu tako da će se tijela ispravno razdvojiti. Nakon što završi propagiranje šoka, mase tijela je potrebno vratiti na prethodnu vrijednost. Valja napomenuti da za dva tijela koja su u kontaktu i nalaze se u istom nivou nijednom još nije postavljena beskonačna masa tako da se među njima rješavanje kontakata obavlja na uobičajen način. Međutim sada je spora konvergencija tijela lokalizirana na manji skup.

  Primjer rada algoritma se može vidjeti na slici 19. Prolaskom kroz graf kontakata u prvom nivou zbog kontakta s podlogom kocka na dnu se zaustavlja te joj se masa postavlja na beskonačnu vrijednost. U sljedećem nivou kocka koja je iznad nje se zaustavlja i masa joj se postavlja na beskonačnu vrijednost i tako se nastavlja sve do zadnjeg nivoa. Vidimo kako nam kontaktni graf omogućuje da se u jednom prolazu ispravno zaustave sva tijela.

Slika 19. Princip rada metode propagiranja šoka. 

  Da bi vidjeli zašto je potrebno prvo izvršiti nekoliko iteracija rješavanja kontakata pomoću propagirajućeg modela prije primjene propagiranja šoka poslužit će primjer na slici 20. Kontaktni graf pokazuje od podloge prema vrhu. Ako bi se sada odmah primijenilo propagiranje šoka, daska bi poprimila beskonačnu masu tako da bi desna teža kocka vidjela dasku beskonačne mase i ne bi mogla gurnuti dasku prema dolje. Propagirajući model nam omogućava da daska dobije ''osjećaj težine''. Korištenjem određenog broja iteracija, daska i tijela u kontaktu s njom dobiju odgovarajuće brzine prije primjene konačnog propagiranja šoka, čime je omogućeno da desna kocka gurne dasku prema dolje i da daska gurne lijevu kocku prema gore.

  Slika 20. Propagirajući model omogućava da teža kocka gurne dasku prema dolje i da zatim daska gurne lijevu kocku prema gore.